#!/usr/bin/env python
# coding: utf-8
# # Finite volume methods-2
#
# * Issues:
# * Fluxes with variable properties
# * See S.V. Patankar "Numerical Heat Transfer and Fluid Flow"
# * Grid decoupling
#
# ## Fluxes with variable properties
#
# * Consider 1-D, steady state heat conduction on a nonuniform grid.
# $$q_e-q_w = S\Delta x.$$
#
#  #
# $$q_e = -k_e\left(\frac{\partial T}{\partial x}\right)_e,$$
# $$q_w = -k_w\left(\frac{\partial T}{\partial x}\right)_w.$$
#
#
# * Consider $q_e$:
#
# $$q_e = -k_e\frac{T_E-T_P}{\delta_e}.$$
#
# * We need $k_e$. How to evaluate it?
#
#
#
#
# * Try linear interpolation:
#
# $$\frac{k_E-k_e}{\delta_{e+}} = \frac{k_E-k_P}{\delta_e},$$
# $$k_e = fk_P + (1-f)k_E,$$
# $$f = \frac{\delta_{e+}}{\delta_e}.$$
#
# Unfortunately, **this does not work very well.**
#
# * The finite volume method is still conservative since $q_e$ is applied to the energy balance for both the P and E cells.
# * But the solution is not physically accurate when applied to systems with variable properties.
#
# ### Case 1
# * Consider the case where cells P and E are different materials.
# * Maybe take E as an insulator
# * Then $k_E = 0$.
# * Expect $q_e = 0$.
# * But linear interpolation to evaluate $q_e$ using $k_e$, as shown above, gives the following:
# $$k_e = \frac{\delta_{e+}}{\delta_e}k_P,$$
# $$q_e = -k_e\frac{T_E-T_P}{\delta_e}\ne0.$$
#
#
# * We expect a temperature profile like the following:
#
#
#
# $$q_e = -k_e\left(\frac{\partial T}{\partial x}\right)_e,$$
# $$q_w = -k_w\left(\frac{\partial T}{\partial x}\right)_w.$$
#
#
# * Consider $q_e$:
#
# $$q_e = -k_e\frac{T_E-T_P}{\delta_e}.$$
#
# * We need $k_e$. How to evaluate it?
#
#
#
#
# * Try linear interpolation:
#
# $$\frac{k_E-k_e}{\delta_{e+}} = \frac{k_E-k_P}{\delta_e},$$
# $$k_e = fk_P + (1-f)k_E,$$
# $$f = \frac{\delta_{e+}}{\delta_e}.$$
#
# Unfortunately, **this does not work very well.**
#
# * The finite volume method is still conservative since $q_e$ is applied to the energy balance for both the P and E cells.
# * But the solution is not physically accurate when applied to systems with variable properties.
#
# ### Case 1
# * Consider the case where cells P and E are different materials.
# * Maybe take E as an insulator
# * Then $k_E = 0$.
# * Expect $q_e = 0$.
# * But linear interpolation to evaluate $q_e$ using $k_e$, as shown above, gives the following:
# $$k_e = \frac{\delta_{e+}}{\delta_e}k_P,$$
# $$q_e = -k_e\frac{T_E-T_P}{\delta_e}\ne0.$$
#
#
# * We expect a temperature profile like the following:
#
# 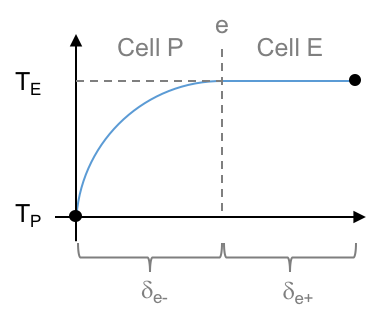 #
# * Notice that no temperature gradient develops in cell E since it is an insulator. This implies zero heat flux.
#
# ### Case 2
# * Now, take a case with $k_E > k_P$.
# * We expect the following temperature profile (assuming uniform properties throughout a given control volume):
#
#
# * Notice that no temperature gradient develops in cell E since it is an insulator. This implies zero heat flux.
#
# ### Case 2
# * Now, take a case with $k_E > k_P$.
# * We expect the following temperature profile (assuming uniform properties throughout a given control volume):
# 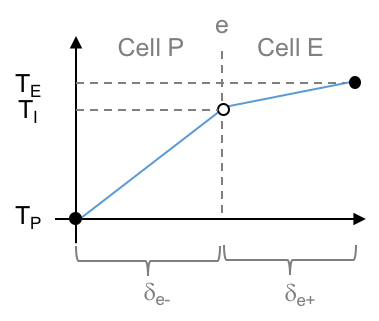 # * here, $T_I$ is an intermediate temperature at the cell face e.
#
# If we use a uniform temperature gradient throught the region of interest, then consider the heat fluxes that this graph implies
#
# * here, $T_I$ is an intermediate temperature at the cell face e.
#
# If we use a uniform temperature gradient throught the region of interest, then consider the heat fluxes that this graph implies
# 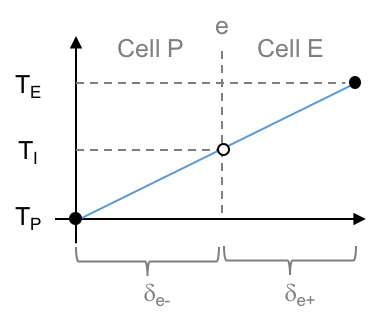 #
# * Denote the heat flux on the left and right sides of e as $q_{e-}$ and $q_{e+}$, respectively.
#
# $$q_{e-} = -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_P\frac{T_E-T_P}{\delta e},$$
#
# $$q_{e+} = -k_E\frac{T_E-T_I}{\delta_{e+}} = -k_E\frac{T_E-T_P}{\delta e}.$$
#
# * Now, since $k_E\ne k_P$ we have $q_{e-}\ne q_{e+}$.
#
# Hence, using (or implying) the same temperature gradient in both cells (materials) gives different heat fluxes in the two cells when using the respective thermal conductivities.
#
# * A linear T profile (same T gradient in both cells) conserves heat flux if the same $k$ is used in both cells.
# * That $k$ could be $k_e$ as evaluated by linear interpolation.
# * But this gives the unphysical behavior of Case 1.
# * And doesn't imply the physical profile of Case 2.
# ### Solution
#
# Find an evaluation of $k_e$, that is physically consistent with heat fluxes through materials of different properties.
#
# That is, find an evaluation of $k_e$ that allows for different temperature gradients to be implied in cells with different conductivities.
# Construct $k_e$ by equating fluxes in the two cells (so that energy is conserved):
# * Allow for an intermediate temperature $T_I = T_e$.
# * Equate the fluxes on the left and right of the interface, and then solve for $T_I$:
#
# $$q_{e-} = q_{e+} \rightarrow -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_E\frac{T_E-T_I}{\delta_{e+}}.$$
#
# $$\rightarrow T_I =frac{\frac{k_P}{\delta_{e-}}T_P + \frac{k_E}{\delta_{e+}}T_E}{\frac{k_P}{\delta_{e-}} + \frac{k_E}{\delta_{e+}}}$$
#
# * Now equate the flux evaluated over both cells P and E (that is, $q_e$), which is written in terms of $k_e$, and equate this to $q_{e-}$.
#
# $$q_e = q_{e-} \rightarrow -k_e\frac{T_E-T_P}{\delta_e} = -k_P\frac{T_I-T_P}{\delta_{e-}}$$
#
# * We insert the expression for $T_I$, and then solve for $k_e$:
#
# $$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$
# $$\color{blue}{k_e = \frac{2k_Pk_E}{k_P+k_E},\,\,\,\mathrm{if}\, \delta_{e-}=\delta_{e+}.}$$
#
# * This is a harmonic mean instead of an arithmetic mean.
# * Use this for finite volume methods with variable $k$, $\mu$, $D$.
# * **Summary**
# $$\color{blue}{q_e = -k_e \frac{T_E-T_P}{\delta_e},}$$
#
# $$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$
#
#
#
# ### Results
# * Now, for $k_E\rightarrow 0$, $k_e\rightarrow 0$, and $q_e\rightarrow 0$ as it should (unlike the linear interpolation).
# * For a case with $k_E\gg k_P$ we have
# $$k_e = \frac{k_P\delta_e}{\delta_{e-}},$$
#
# $$q_e = -\frac{k_P\delta_e}{\delta_{e-}}\frac{T_E-T_P}{\delta_{e}} = -k_P\frac{T_E-T_P}{\delta_{e-}}.$$
#
# * This implies that all the change happens in the P cell, with the E cell offering no resistence. Good! This is consistent with the physical situation.
#
#
# ## Grid decoupling
# * There is a problem with first derivatives.
# * Consider cells W, P, E and a convective flux term where $v$ is velocity and $f$ is some variable.
#
# ```
# |---W---|---P---|---E---|
# w e
# ```
#
# $$\frac{\partial vf}{\partial x}.$$
#
# * Integrate this over cell P
# $$(vf)_e-(vf)_w$$
# * Then interpolate to find $(vf)_e$ and $(vf)_w$:
# $$ \frac{v_Ef_E+v_Pf_P}{2} - \frac{v_Pf_P + v_Wf_W}{2},$$
# $$ \frac{v_Ef_E-v_Wf_W}{2}.$$
#
# * Note how this totally skips the P cell.
#
#
# * If we have a $vf$ field as shown below, the first derivative of $vf$ will be zero everywhere and this profile will persist.
#
# ```
# |---5---|---3---|---5---|---3---|---5---|
# ```
#
# * This can happen in 2D or 3D:
# ```
# |-----|-----|-----|
# | 8 | 3 | 8 |
# |-----|-----|-----|
# | 3 | 5 | 3 |
# |-----|-----|-----|
# | 8 | 3 | 8 |
# |-----|-----|-----|
# ```
#
# * Or, suppose we take a smooth solution and add a checkerboard pattern (from noise, or errors, etc.), this patter could persist, or even grow.
#
# * This happens with pressure P in the fluid equations. The $\nabla P$ term gives $P_e-P_w$ hence $(P_E-P_W)/2$.
# * Pressure gradients drive velocity, and we'd like pressure to not skip cells. We don't want a pressure checkerboard to be preserved or to grow.
#
#
#
# * **Remedy: Use a staggered grid.**
# * Velocity is solved on the orange grid cells (v-cells) and
# * Pressure is solved on the black grid cells (P-cells).
# * When considering the velocity equation we are using the orange grid (v-cells). Then $dP/dx \rightarrow (P_e-P_w)$, but these values are known directly on the black grid (P-cells) and no interpolation is necessary, and no checkerboarding occurs.
#
#
#
# * Denote the heat flux on the left and right sides of e as $q_{e-}$ and $q_{e+}$, respectively.
#
# $$q_{e-} = -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_P\frac{T_E-T_P}{\delta e},$$
#
# $$q_{e+} = -k_E\frac{T_E-T_I}{\delta_{e+}} = -k_E\frac{T_E-T_P}{\delta e}.$$
#
# * Now, since $k_E\ne k_P$ we have $q_{e-}\ne q_{e+}$.
#
# Hence, using (or implying) the same temperature gradient in both cells (materials) gives different heat fluxes in the two cells when using the respective thermal conductivities.
#
# * A linear T profile (same T gradient in both cells) conserves heat flux if the same $k$ is used in both cells.
# * That $k$ could be $k_e$ as evaluated by linear interpolation.
# * But this gives the unphysical behavior of Case 1.
# * And doesn't imply the physical profile of Case 2.
# ### Solution
#
# Find an evaluation of $k_e$, that is physically consistent with heat fluxes through materials of different properties.
#
# That is, find an evaluation of $k_e$ that allows for different temperature gradients to be implied in cells with different conductivities.
# Construct $k_e$ by equating fluxes in the two cells (so that energy is conserved):
# * Allow for an intermediate temperature $T_I = T_e$.
# * Equate the fluxes on the left and right of the interface, and then solve for $T_I$:
#
# $$q_{e-} = q_{e+} \rightarrow -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_E\frac{T_E-T_I}{\delta_{e+}}.$$
#
# $$\rightarrow T_I =frac{\frac{k_P}{\delta_{e-}}T_P + \frac{k_E}{\delta_{e+}}T_E}{\frac{k_P}{\delta_{e-}} + \frac{k_E}{\delta_{e+}}}$$
#
# * Now equate the flux evaluated over both cells P and E (that is, $q_e$), which is written in terms of $k_e$, and equate this to $q_{e-}$.
#
# $$q_e = q_{e-} \rightarrow -k_e\frac{T_E-T_P}{\delta_e} = -k_P\frac{T_I-T_P}{\delta_{e-}}$$
#
# * We insert the expression for $T_I$, and then solve for $k_e$:
#
# $$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$
# $$\color{blue}{k_e = \frac{2k_Pk_E}{k_P+k_E},\,\,\,\mathrm{if}\, \delta_{e-}=\delta_{e+}.}$$
#
# * This is a harmonic mean instead of an arithmetic mean.
# * Use this for finite volume methods with variable $k$, $\mu$, $D$.
# * **Summary**
# $$\color{blue}{q_e = -k_e \frac{T_E-T_P}{\delta_e},}$$
#
# $$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$
#
#
#
# ### Results
# * Now, for $k_E\rightarrow 0$, $k_e\rightarrow 0$, and $q_e\rightarrow 0$ as it should (unlike the linear interpolation).
# * For a case with $k_E\gg k_P$ we have
# $$k_e = \frac{k_P\delta_e}{\delta_{e-}},$$
#
# $$q_e = -\frac{k_P\delta_e}{\delta_{e-}}\frac{T_E-T_P}{\delta_{e}} = -k_P\frac{T_E-T_P}{\delta_{e-}}.$$
#
# * This implies that all the change happens in the P cell, with the E cell offering no resistence. Good! This is consistent with the physical situation.
#
#
# ## Grid decoupling
# * There is a problem with first derivatives.
# * Consider cells W, P, E and a convective flux term where $v$ is velocity and $f$ is some variable.
#
# ```
# |---W---|---P---|---E---|
# w e
# ```
#
# $$\frac{\partial vf}{\partial x}.$$
#
# * Integrate this over cell P
# $$(vf)_e-(vf)_w$$
# * Then interpolate to find $(vf)_e$ and $(vf)_w$:
# $$ \frac{v_Ef_E+v_Pf_P}{2} - \frac{v_Pf_P + v_Wf_W}{2},$$
# $$ \frac{v_Ef_E-v_Wf_W}{2}.$$
#
# * Note how this totally skips the P cell.
#
#
# * If we have a $vf$ field as shown below, the first derivative of $vf$ will be zero everywhere and this profile will persist.
#
# ```
# |---5---|---3---|---5---|---3---|---5---|
# ```
#
# * This can happen in 2D or 3D:
# ```
# |-----|-----|-----|
# | 8 | 3 | 8 |
# |-----|-----|-----|
# | 3 | 5 | 3 |
# |-----|-----|-----|
# | 8 | 3 | 8 |
# |-----|-----|-----|
# ```
#
# * Or, suppose we take a smooth solution and add a checkerboard pattern (from noise, or errors, etc.), this patter could persist, or even grow.
#
# * This happens with pressure P in the fluid equations. The $\nabla P$ term gives $P_e-P_w$ hence $(P_E-P_W)/2$.
# * Pressure gradients drive velocity, and we'd like pressure to not skip cells. We don't want a pressure checkerboard to be preserved or to grow.
#
#
#
# * **Remedy: Use a staggered grid.**
# * Velocity is solved on the orange grid cells (v-cells) and
# * Pressure is solved on the black grid cells (P-cells).
# * When considering the velocity equation we are using the orange grid (v-cells). Then $dP/dx \rightarrow (P_e-P_w)$, but these values are known directly on the black grid (P-cells) and no interpolation is necessary, and no checkerboarding occurs.
#
# 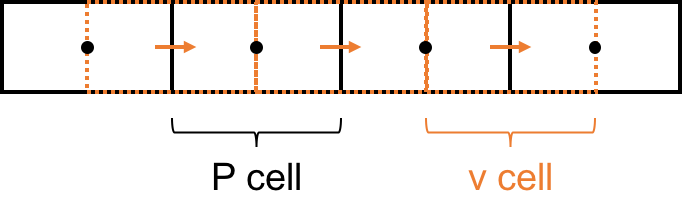 #
#
#
# * In 2-D, we have P-cells in the center, u-cells shifted to the left, and v-cells shifted down.
#
#
#
#
# * In 2-D, we have P-cells in the center, u-cells shifted to the left, and v-cells shifted down.
# 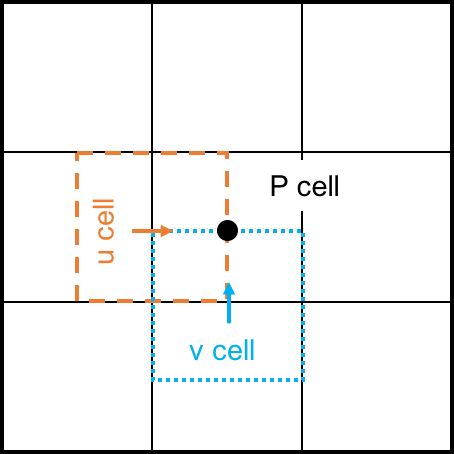 #
# * Normally, scalars such as pressure, temperature, species mass fractions, etc. are evaluated using P-cells, and velocity vectors are on u-cells, v-cells, and w-cells.
# * This is convenient for discretization, and numerically very stable.
#
# **Grids are called either staggered or collocated.**
#
# * Normally, scalars such as pressure, temperature, species mass fractions, etc. are evaluated using P-cells, and velocity vectors are on u-cells, v-cells, and w-cells.
# * This is convenient for discretization, and numerically very stable.
#
# **Grids are called either staggered or collocated.**
 #
# $$q_e = -k_e\left(\frac{\partial T}{\partial x}\right)_e,$$
# $$q_w = -k_w\left(\frac{\partial T}{\partial x}\right)_w.$$
#
#
# * Consider $q_e$:
#
# $$q_e = -k_e\frac{T_E-T_P}{\delta_e}.$$
#
# * We need $k_e$. How to evaluate it?
#
#
#
#
# * Try linear interpolation:
#
# $$\frac{k_E-k_e}{\delta_{e+}} = \frac{k_E-k_P}{\delta_e},$$
# $$k_e = fk_P + (1-f)k_E,$$
# $$f = \frac{\delta_{e+}}{\delta_e}.$$
#
# Unfortunately, **this does not work very well.**
#
# * The finite volume method is still conservative since $q_e$ is applied to the energy balance for both the P and E cells.
# * But the solution is not physically accurate when applied to systems with variable properties.
#
# ### Case 1
# * Consider the case where cells P and E are different materials.
# * Maybe take E as an insulator
# * Then $k_E = 0$.
# * Expect $q_e = 0$.
# * But linear interpolation to evaluate $q_e$ using $k_e$, as shown above, gives the following:
# $$k_e = \frac{\delta_{e+}}{\delta_e}k_P,$$
# $$q_e = -k_e\frac{T_E-T_P}{\delta_e}\ne0.$$
#
#
# * We expect a temperature profile like the following:
#
#
#
# $$q_e = -k_e\left(\frac{\partial T}{\partial x}\right)_e,$$
# $$q_w = -k_w\left(\frac{\partial T}{\partial x}\right)_w.$$
#
#
# * Consider $q_e$:
#
# $$q_e = -k_e\frac{T_E-T_P}{\delta_e}.$$
#
# * We need $k_e$. How to evaluate it?
#
#
#
#
# * Try linear interpolation:
#
# $$\frac{k_E-k_e}{\delta_{e+}} = \frac{k_E-k_P}{\delta_e},$$
# $$k_e = fk_P + (1-f)k_E,$$
# $$f = \frac{\delta_{e+}}{\delta_e}.$$
#
# Unfortunately, **this does not work very well.**
#
# * The finite volume method is still conservative since $q_e$ is applied to the energy balance for both the P and E cells.
# * But the solution is not physically accurate when applied to systems with variable properties.
#
# ### Case 1
# * Consider the case where cells P and E are different materials.
# * Maybe take E as an insulator
# * Then $k_E = 0$.
# * Expect $q_e = 0$.
# * But linear interpolation to evaluate $q_e$ using $k_e$, as shown above, gives the following:
# $$k_e = \frac{\delta_{e+}}{\delta_e}k_P,$$
# $$q_e = -k_e\frac{T_E-T_P}{\delta_e}\ne0.$$
#
#
# * We expect a temperature profile like the following:
#
#  #
# * Notice that no temperature gradient develops in cell E since it is an insulator. This implies zero heat flux.
#
# ### Case 2
# * Now, take a case with $k_E > k_P$.
# * We expect the following temperature profile (assuming uniform properties throughout a given control volume):
#
#
# * Notice that no temperature gradient develops in cell E since it is an insulator. This implies zero heat flux.
#
# ### Case 2
# * Now, take a case with $k_E > k_P$.
# * We expect the following temperature profile (assuming uniform properties throughout a given control volume):
#  # * here, $T_I$ is an intermediate temperature at the cell face e.
#
# If we use a uniform temperature gradient throught the region of interest, then consider the heat fluxes that this graph implies
#
# * here, $T_I$ is an intermediate temperature at the cell face e.
#
# If we use a uniform temperature gradient throught the region of interest, then consider the heat fluxes that this graph implies
#  #
# * Denote the heat flux on the left and right sides of e as $q_{e-}$ and $q_{e+}$, respectively.
#
# $$q_{e-} = -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_P\frac{T_E-T_P}{\delta e},$$
#
# $$q_{e+} = -k_E\frac{T_E-T_I}{\delta_{e+}} = -k_E\frac{T_E-T_P}{\delta e}.$$
#
# * Now, since $k_E\ne k_P$ we have $q_{e-}\ne q_{e+}$.
#
# Hence, using (or implying) the same temperature gradient in both cells (materials) gives different heat fluxes in the two cells when using the respective thermal conductivities.
#
# * A linear T profile (same T gradient in both cells) conserves heat flux if the same $k$ is used in both cells.
# * That $k$ could be $k_e$ as evaluated by linear interpolation.
# * But this gives the unphysical behavior of Case 1.
# * And doesn't imply the physical profile of Case 2.
# ### Solution
#
# Find an evaluation of $k_e$, that is physically consistent with heat fluxes through materials of different properties.
#
# That is, find an evaluation of $k_e$ that allows for different temperature gradients to be implied in cells with different conductivities.
# Construct $k_e$ by equating fluxes in the two cells (so that energy is conserved):
# * Allow for an intermediate temperature $T_I = T_e$.
# * Equate the fluxes on the left and right of the interface, and then solve for $T_I$:
#
# $$q_{e-} = q_{e+} \rightarrow -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_E\frac{T_E-T_I}{\delta_{e+}}.$$
#
# $$\rightarrow T_I =frac{\frac{k_P}{\delta_{e-}}T_P + \frac{k_E}{\delta_{e+}}T_E}{\frac{k_P}{\delta_{e-}} + \frac{k_E}{\delta_{e+}}}$$
#
# * Now equate the flux evaluated over both cells P and E (that is, $q_e$), which is written in terms of $k_e$, and equate this to $q_{e-}$.
#
# $$q_e = q_{e-} \rightarrow -k_e\frac{T_E-T_P}{\delta_e} = -k_P\frac{T_I-T_P}{\delta_{e-}}$$
#
# * We insert the expression for $T_I$, and then solve for $k_e$:
#
# $$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$
# $$\color{blue}{k_e = \frac{2k_Pk_E}{k_P+k_E},\,\,\,\mathrm{if}\, \delta_{e-}=\delta_{e+}.}$$
#
# * This is a harmonic mean instead of an arithmetic mean.
# * Use this for finite volume methods with variable $k$, $\mu$, $D$.
# * **Summary**
# $$\color{blue}{q_e = -k_e \frac{T_E-T_P}{\delta_e},}$$
#
# $$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$
#
#
#
# ### Results
# * Now, for $k_E\rightarrow 0$, $k_e\rightarrow 0$, and $q_e\rightarrow 0$ as it should (unlike the linear interpolation).
# * For a case with $k_E\gg k_P$ we have
# $$k_e = \frac{k_P\delta_e}{\delta_{e-}},$$
#
# $$q_e = -\frac{k_P\delta_e}{\delta_{e-}}\frac{T_E-T_P}{\delta_{e}} = -k_P\frac{T_E-T_P}{\delta_{e-}}.$$
#
# * This implies that all the change happens in the P cell, with the E cell offering no resistence. Good! This is consistent with the physical situation.
#
#
# ## Grid decoupling
# * There is a problem with first derivatives.
# * Consider cells W, P, E and a convective flux term where $v$ is velocity and $f$ is some variable.
#
# ```
# |---W---|---P---|---E---|
# w e
# ```
#
# $$\frac{\partial vf}{\partial x}.$$
#
# * Integrate this over cell P
# $$(vf)_e-(vf)_w$$
# * Then interpolate to find $(vf)_e$ and $(vf)_w$:
# $$ \frac{v_Ef_E+v_Pf_P}{2} - \frac{v_Pf_P + v_Wf_W}{2},$$
# $$ \frac{v_Ef_E-v_Wf_W}{2}.$$
#
# * Note how this totally skips the P cell.
#
#
# * If we have a $vf$ field as shown below, the first derivative of $vf$ will be zero everywhere and this profile will persist.
#
# ```
# |---5---|---3---|---5---|---3---|---5---|
# ```
#
# * This can happen in 2D or 3D:
# ```
# |-----|-----|-----|
# | 8 | 3 | 8 |
# |-----|-----|-----|
# | 3 | 5 | 3 |
# |-----|-----|-----|
# | 8 | 3 | 8 |
# |-----|-----|-----|
# ```
#
# * Or, suppose we take a smooth solution and add a checkerboard pattern (from noise, or errors, etc.), this patter could persist, or even grow.
#
# * This happens with pressure P in the fluid equations. The $\nabla P$ term gives $P_e-P_w$ hence $(P_E-P_W)/2$.
# * Pressure gradients drive velocity, and we'd like pressure to not skip cells. We don't want a pressure checkerboard to be preserved or to grow.
#
#
#
# * **Remedy: Use a staggered grid.**
# * Velocity is solved on the orange grid cells (v-cells) and
# * Pressure is solved on the black grid cells (P-cells).
# * When considering the velocity equation we are using the orange grid (v-cells). Then $dP/dx \rightarrow (P_e-P_w)$, but these values are known directly on the black grid (P-cells) and no interpolation is necessary, and no checkerboarding occurs.
#
#
#
# * Denote the heat flux on the left and right sides of e as $q_{e-}$ and $q_{e+}$, respectively.
#
# $$q_{e-} = -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_P\frac{T_E-T_P}{\delta e},$$
#
# $$q_{e+} = -k_E\frac{T_E-T_I}{\delta_{e+}} = -k_E\frac{T_E-T_P}{\delta e}.$$
#
# * Now, since $k_E\ne k_P$ we have $q_{e-}\ne q_{e+}$.
#
# Hence, using (or implying) the same temperature gradient in both cells (materials) gives different heat fluxes in the two cells when using the respective thermal conductivities.
#
# * A linear T profile (same T gradient in both cells) conserves heat flux if the same $k$ is used in both cells.
# * That $k$ could be $k_e$ as evaluated by linear interpolation.
# * But this gives the unphysical behavior of Case 1.
# * And doesn't imply the physical profile of Case 2.
# ### Solution
#
# Find an evaluation of $k_e$, that is physically consistent with heat fluxes through materials of different properties.
#
# That is, find an evaluation of $k_e$ that allows for different temperature gradients to be implied in cells with different conductivities.
# Construct $k_e$ by equating fluxes in the two cells (so that energy is conserved):
# * Allow for an intermediate temperature $T_I = T_e$.
# * Equate the fluxes on the left and right of the interface, and then solve for $T_I$:
#
# $$q_{e-} = q_{e+} \rightarrow -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_E\frac{T_E-T_I}{\delta_{e+}}.$$
#
# $$\rightarrow T_I =frac{\frac{k_P}{\delta_{e-}}T_P + \frac{k_E}{\delta_{e+}}T_E}{\frac{k_P}{\delta_{e-}} + \frac{k_E}{\delta_{e+}}}$$
#
# * Now equate the flux evaluated over both cells P and E (that is, $q_e$), which is written in terms of $k_e$, and equate this to $q_{e-}$.
#
# $$q_e = q_{e-} \rightarrow -k_e\frac{T_E-T_P}{\delta_e} = -k_P\frac{T_I-T_P}{\delta_{e-}}$$
#
# * We insert the expression for $T_I$, and then solve for $k_e$:
#
# $$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$
# $$\color{blue}{k_e = \frac{2k_Pk_E}{k_P+k_E},\,\,\,\mathrm{if}\, \delta_{e-}=\delta_{e+}.}$$
#
# * This is a harmonic mean instead of an arithmetic mean.
# * Use this for finite volume methods with variable $k$, $\mu$, $D$.
# * **Summary**
# $$\color{blue}{q_e = -k_e \frac{T_E-T_P}{\delta_e},}$$
#
# $$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$
#
#
#
# ### Results
# * Now, for $k_E\rightarrow 0$, $k_e\rightarrow 0$, and $q_e\rightarrow 0$ as it should (unlike the linear interpolation).
# * For a case with $k_E\gg k_P$ we have
# $$k_e = \frac{k_P\delta_e}{\delta_{e-}},$$
#
# $$q_e = -\frac{k_P\delta_e}{\delta_{e-}}\frac{T_E-T_P}{\delta_{e}} = -k_P\frac{T_E-T_P}{\delta_{e-}}.$$
#
# * This implies that all the change happens in the P cell, with the E cell offering no resistence. Good! This is consistent with the physical situation.
#
#
# ## Grid decoupling
# * There is a problem with first derivatives.
# * Consider cells W, P, E and a convective flux term where $v$ is velocity and $f$ is some variable.
#
# ```
# |---W---|---P---|---E---|
# w e
# ```
#
# $$\frac{\partial vf}{\partial x}.$$
#
# * Integrate this over cell P
# $$(vf)_e-(vf)_w$$
# * Then interpolate to find $(vf)_e$ and $(vf)_w$:
# $$ \frac{v_Ef_E+v_Pf_P}{2} - \frac{v_Pf_P + v_Wf_W}{2},$$
# $$ \frac{v_Ef_E-v_Wf_W}{2}.$$
#
# * Note how this totally skips the P cell.
#
#
# * If we have a $vf$ field as shown below, the first derivative of $vf$ will be zero everywhere and this profile will persist.
#
# ```
# |---5---|---3---|---5---|---3---|---5---|
# ```
#
# * This can happen in 2D or 3D:
# ```
# |-----|-----|-----|
# | 8 | 3 | 8 |
# |-----|-----|-----|
# | 3 | 5 | 3 |
# |-----|-----|-----|
# | 8 | 3 | 8 |
# |-----|-----|-----|
# ```
#
# * Or, suppose we take a smooth solution and add a checkerboard pattern (from noise, or errors, etc.), this patter could persist, or even grow.
#
# * This happens with pressure P in the fluid equations. The $\nabla P$ term gives $P_e-P_w$ hence $(P_E-P_W)/2$.
# * Pressure gradients drive velocity, and we'd like pressure to not skip cells. We don't want a pressure checkerboard to be preserved or to grow.
#
#
#
# * **Remedy: Use a staggered grid.**
# * Velocity is solved on the orange grid cells (v-cells) and
# * Pressure is solved on the black grid cells (P-cells).
# * When considering the velocity equation we are using the orange grid (v-cells). Then $dP/dx \rightarrow (P_e-P_w)$, but these values are known directly on the black grid (P-cells) and no interpolation is necessary, and no checkerboarding occurs.
#
#  #
#
#
# * In 2-D, we have P-cells in the center, u-cells shifted to the left, and v-cells shifted down.
#
#
#
#
# * In 2-D, we have P-cells in the center, u-cells shifted to the left, and v-cells shifted down.
#  #
# * Normally, scalars such as pressure, temperature, species mass fractions, etc. are evaluated using P-cells, and velocity vectors are on u-cells, v-cells, and w-cells.
# * This is convenient for discretization, and numerically very stable.
#
# **Grids are called either staggered or collocated.**
#
# * Normally, scalars such as pressure, temperature, species mass fractions, etc. are evaluated using P-cells, and velocity vectors are on u-cells, v-cells, and w-cells.
# * This is convenient for discretization, and numerically very stable.
#
# **Grids are called either staggered or collocated.**