#!/usr/bin/env python
# coding: utf-8
# [Oregon Curriculum Network](http://www.4dsolutions.net/ocn)
# [Discovering Math with Python](Introduction.ipynb)
#
#
# # FOCUSING ON THE S FACTOR
# #### $\phi$ DOODLES Using $\LaTeX$
#
#  #
# First, some identity checks (not proofs), using Decimal objects:
#
# $\sqrt{2}-(\sqrt{2}(\phi^{-3}))= 2\sqrt{2}(\phi^{-2})$
#
# $(\phi^{-2})+(\phi^{-3})+(\phi^{2}) = 1$
# In[1]:
from math import sqrt as rt2
from decimal import Decimal, getcontext
context = getcontext()
context.prec = 50
# In[2]:
one = Decimal(1) # 28 digits of precision by default, more on tap
two = Decimal(2)
three = Decimal(3)
five = Decimal(5)
nine = Decimal(9)
eight = Decimal(8)
sqrt2 = two.sqrt()
sqrt5 = five.sqrt()
Ø = (one + sqrt5)/two
S3 = (nine/eight).sqrt() # Got Synergetics?
# In showing off the Decimal type, I'm advertising high precision, but not "infinite precision". Please be tolerant of our epsilons (tiny abberations).
# In[3]:
(Ø**-2) + (Ø**-3) + ( Ø**-2)
# In[4]:
sqrt2 - sqrt2 * Ø**-3
# ## JITTERBUG TRANSFORMATION
#
# We call this the S Factor by the way. VE:Icosa :: S:E is what to remember. VE is the 12-around-1 nuclear sphere based agglomeration whereas Icosa is dervied from Jitterbugging, a mathematical transformation with a more technical name if you're a math snob (I can be).
#
#
#
# First, some identity checks (not proofs), using Decimal objects:
#
# $\sqrt{2}-(\sqrt{2}(\phi^{-3}))= 2\sqrt{2}(\phi^{-2})$
#
# $(\phi^{-2})+(\phi^{-3})+(\phi^{2}) = 1$
# In[1]:
from math import sqrt as rt2
from decimal import Decimal, getcontext
context = getcontext()
context.prec = 50
# In[2]:
one = Decimal(1) # 28 digits of precision by default, more on tap
two = Decimal(2)
three = Decimal(3)
five = Decimal(5)
nine = Decimal(9)
eight = Decimal(8)
sqrt2 = two.sqrt()
sqrt5 = five.sqrt()
Ø = (one + sqrt5)/two
S3 = (nine/eight).sqrt() # Got Synergetics?
# In showing off the Decimal type, I'm advertising high precision, but not "infinite precision". Please be tolerant of our epsilons (tiny abberations).
# In[3]:
(Ø**-2) + (Ø**-3) + ( Ø**-2)
# In[4]:
sqrt2 - sqrt2 * Ø**-3
# ## JITTERBUG TRANSFORMATION
#
# We call this the S Factor by the way. VE:Icosa :: S:E is what to remember. VE is the 12-around-1 nuclear sphere based agglomeration whereas Icosa is dervied from Jitterbugging, a mathematical transformation with a more technical name if you're a math snob (I can be).
#
#  # In[5]:
two * sqrt2 * (Ø**-2)
# In[6]:
icosa = five * sqrt2 * Ø ** 2
icosa
# In[7]:
ve = Decimal(20)
# In[8]:
s_factor = ve / icosa
# In[9]:
s_factor # see?
# ## "SMALLGUY"
#
# Above is an expression for the volume of said Icosa in tetravolumes.
#
# We may think of it as "two applications of the S-Factor bigger" than a smaller cubocta, with edges, get this, equal in magnitude to the *volume* of the edge 2 icosa.
#
# David Koski and I got to calling this cubocta "SmallGuy" (feel free to substitute your own moniker).
#
# The Concentric Hierarchy has a *Sesame Street* flavor (kids' TV show) in some walkx of life, lending to our penchant for colloquialisms.
# In[10]:
SmallGuy = icosa * one/s_factor * one/s_factor
SmallGuy
# Another way to reach the SmallGuy is to start with the volume 20 cubocta and shrink its edges by the S Factor, which means volume shrinks by a factor of the reciprocal of said S Factor to the 3rd power or $1/s\_factor ^{3}$
# In[11]:
ve * (one/s_factor)**3
# In[12]:
SmallGuy_edge = two * (one/s_factor) # effect on edges
SmallGuy_edge
# ## RHOMBIC TRIACONTAHEDRON (RT)
#
#
# In[5]:
two * sqrt2 * (Ø**-2)
# In[6]:
icosa = five * sqrt2 * Ø ** 2
icosa
# In[7]:
ve = Decimal(20)
# In[8]:
s_factor = ve / icosa
# In[9]:
s_factor # see?
# ## "SMALLGUY"
#
# Above is an expression for the volume of said Icosa in tetravolumes.
#
# We may think of it as "two applications of the S-Factor bigger" than a smaller cubocta, with edges, get this, equal in magnitude to the *volume* of the edge 2 icosa.
#
# David Koski and I got to calling this cubocta "SmallGuy" (feel free to substitute your own moniker).
#
# The Concentric Hierarchy has a *Sesame Street* flavor (kids' TV show) in some walkx of life, lending to our penchant for colloquialisms.
# In[10]:
SmallGuy = icosa * one/s_factor * one/s_factor
SmallGuy
# Another way to reach the SmallGuy is to start with the volume 20 cubocta and shrink its edges by the S Factor, which means volume shrinks by a factor of the reciprocal of said S Factor to the 3rd power or $1/s\_factor ^{3}$
# In[11]:
ve * (one/s_factor)**3
# In[12]:
SmallGuy_edge = two * (one/s_factor) # effect on edges
SmallGuy_edge
# ## RHOMBIC TRIACONTAHEDRON (RT)
#
# 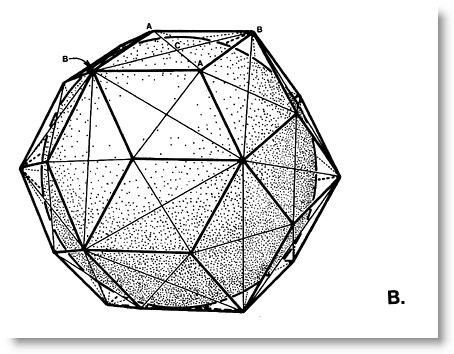 # In[13]:
superRT = ve * S3
superRT
# S3 is our conversion constant for going between XYZ cube volumes and [IVM](https://github.com/4dsolutions/Python5/blob/master/Generating%20the%20FCC.ipynb) tetra volumes. The two mensuration systems each have their own unit volume, by convention a .5 radius edge cube versus a 1.0 diametered edged tetrahedron, or use edges 1 and 2 if preferred, their ratio will be the same, with the cube a bit bigger.
#
#
# In[13]:
superRT = ve * S3
superRT
# S3 is our conversion constant for going between XYZ cube volumes and [IVM](https://github.com/4dsolutions/Python5/blob/master/Generating%20the%20FCC.ipynb) tetra volumes. The two mensuration systems each have their own unit volume, by convention a .5 radius edge cube versus a 1.0 diametered edged tetrahedron, or use edges 1 and 2 if preferred, their ratio will be the same, with the cube a bit bigger.
#
# 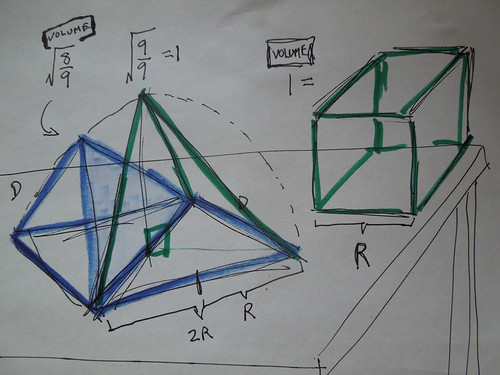 #
# SuperRT is the RT (rhombic triacontahedron) formed by the Icosa and its dual, the Pentagonal Dodecahedron, the two five-fold symmetric shapes in [the Platonic set](https://youtu.be/vk-cpknOz9E) of five polys. The Icosa we're talking about is the one above, derived from the VE of volume 20, through Jitterbugging.
#
# If we shrink SuperRT down by $\phi^{-3}$ volume-wise (all edges are now $\phi^{-1}$ their initial length), and carve it into 120 modules (60 left, 60 right), then lo and behold, we have the E modules.
#
# Another expression for SuperRT volume is $15\sqrt{2}$.
# In[14]:
Decimal('15') * sqrt2
# ## E MODULE
#
#
#
# SuperRT is the RT (rhombic triacontahedron) formed by the Icosa and its dual, the Pentagonal Dodecahedron, the two five-fold symmetric shapes in [the Platonic set](https://youtu.be/vk-cpknOz9E) of five polys. The Icosa we're talking about is the one above, derived from the VE of volume 20, through Jitterbugging.
#
# If we shrink SuperRT down by $\phi^{-3}$ volume-wise (all edges are now $\phi^{-1}$ their initial length), and carve it into 120 modules (60 left, 60 right), then lo and behold, we have the E modules.
#
# Another expression for SuperRT volume is $15\sqrt{2}$.
# In[14]:
Decimal('15') * sqrt2
# ## E MODULE
#
# 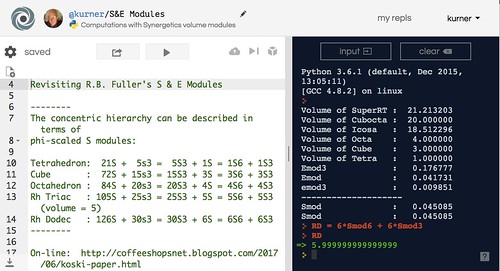 # In[15]:
emod = (superRT * Ø**-3)/Decimal(120)
# In[16]:
emod
# In[17]:
smod = emod * s_factor
smod
# In[18]:
smod/emod
# The S factor again, yes?
#
# $\sqrt{2}-(\sqrt{2}(\phi^{-3}))= 2\sqrt{2}(\phi^{-2})$ = S Factor.
#
# Another expression for the S Factor is $24E + 8e3$ where E means emod, and $e3$ means $E * \phi^{-3}$.
# In[19]:
Decimal(24) * emod + Decimal(8) * emod * Ø**-3
# ## S MODULE
#
# Now lets shrink the 20 volumed VE by halving all edges, reducing volume by a factor of 8, to 2.5
#
# In[20]:
small_ve = ve / Decimal(8)
#
# In[15]:
emod = (superRT * Ø**-3)/Decimal(120)
# In[16]:
emod
# In[17]:
smod = emod * s_factor
smod
# In[18]:
smod/emod
# The S factor again, yes?
#
# $\sqrt{2}-(\sqrt{2}(\phi^{-3}))= 2\sqrt{2}(\phi^{-2})$ = S Factor.
#
# Another expression for the S Factor is $24E + 8e3$ where E means emod, and $e3$ means $E * \phi^{-3}$.
# In[19]:
Decimal(24) * emod + Decimal(8) * emod * Ø**-3
# ## S MODULE
#
# Now lets shrink the 20 volumed VE by halving all edges, reducing volume by a factor of 8, to 2.5
#
# In[20]:
small_ve = ve / Decimal(8)
#  #
# As every grade schooler knows, if at all aware of their heritage, said VE inscribes inside the octahedron of volume 4, as does an Icosahedron with flush faces. We do a kind of jitterbugging that makes the VE larger instead of smaller. Two applications of the S Factor does the trick.
# In[21]:
skew_icosa = small_ve * s_factor * s_factor
# In[22]:
skew_icosa
# In[23]:
skew_icosa + (24 * smod)
# The figure below is an S-Factor radius, meaning from the center to each diamond face center on the surface.
#
#
#
# As every grade schooler knows, if at all aware of their heritage, said VE inscribes inside the octahedron of volume 4, as does an Icosahedron with flush faces. We do a kind of jitterbugging that makes the VE larger instead of smaller. Two applications of the S Factor does the trick.
# In[21]:
skew_icosa = small_ve * s_factor * s_factor
# In[22]:
skew_icosa
# In[23]:
skew_icosa + (24 * smod)
# The figure below is an S-Factor radius, meaning from the center to each diamond face center on the surface.
#
#  #
# by D.B. Koski using vZome
# David Koski writes (on Facebook):
#
# The volume 4, edge 2 octahedron, has a volume of 4 tetrahedral units or 84S + 20s3 modules
#
# S = $(\phi^{-5})/2$ = .045084
#
# s3 = $(\phi^{-8})/2$ = .010643
#
# The icosahedron inside of this octahedron has a volume of 84S+20s3 - 24S = 60S+20s3 = 2.917960 = $20(\phi^{-4})$.
# Surprisingly, this icosahedron has an edge of 1.08036 or the Sfactor!
# In[24]:
Decimal(60) * smod + Decimal(20) * smod * Ø**-3
# In[25]:
Decimal(20) * Ø**-4
# ## A MODULE
#
# The A and B modules have the same volume (1/24), as does the [T modules](http://www.grunch.net/synergetics/tmod.html). We review these in other Notebooks.
#
#  #
#
#
# 3D Print Me!
 #
# First, some identity checks (not proofs), using Decimal objects:
#
# $\sqrt{2}-(\sqrt{2}(\phi^{-3}))= 2\sqrt{2}(\phi^{-2})$
#
# $(\phi^{-2})+(\phi^{-3})+(\phi^{2}) = 1$
# In[1]:
from math import sqrt as rt2
from decimal import Decimal, getcontext
context = getcontext()
context.prec = 50
# In[2]:
one = Decimal(1) # 28 digits of precision by default, more on tap
two = Decimal(2)
three = Decimal(3)
five = Decimal(5)
nine = Decimal(9)
eight = Decimal(8)
sqrt2 = two.sqrt()
sqrt5 = five.sqrt()
Ø = (one + sqrt5)/two
S3 = (nine/eight).sqrt() # Got Synergetics?
# In showing off the Decimal type, I'm advertising high precision, but not "infinite precision". Please be tolerant of our epsilons (tiny abberations).
# In[3]:
(Ø**-2) + (Ø**-3) + ( Ø**-2)
# In[4]:
sqrt2 - sqrt2 * Ø**-3
# ## JITTERBUG TRANSFORMATION
#
# We call this the S Factor by the way. VE:Icosa :: S:E is what to remember. VE is the 12-around-1 nuclear sphere based agglomeration whereas Icosa is dervied from Jitterbugging, a mathematical transformation with a more technical name if you're a math snob (I can be).
#
#
#
# First, some identity checks (not proofs), using Decimal objects:
#
# $\sqrt{2}-(\sqrt{2}(\phi^{-3}))= 2\sqrt{2}(\phi^{-2})$
#
# $(\phi^{-2})+(\phi^{-3})+(\phi^{2}) = 1$
# In[1]:
from math import sqrt as rt2
from decimal import Decimal, getcontext
context = getcontext()
context.prec = 50
# In[2]:
one = Decimal(1) # 28 digits of precision by default, more on tap
two = Decimal(2)
three = Decimal(3)
five = Decimal(5)
nine = Decimal(9)
eight = Decimal(8)
sqrt2 = two.sqrt()
sqrt5 = five.sqrt()
Ø = (one + sqrt5)/two
S3 = (nine/eight).sqrt() # Got Synergetics?
# In showing off the Decimal type, I'm advertising high precision, but not "infinite precision". Please be tolerant of our epsilons (tiny abberations).
# In[3]:
(Ø**-2) + (Ø**-3) + ( Ø**-2)
# In[4]:
sqrt2 - sqrt2 * Ø**-3
# ## JITTERBUG TRANSFORMATION
#
# We call this the S Factor by the way. VE:Icosa :: S:E is what to remember. VE is the 12-around-1 nuclear sphere based agglomeration whereas Icosa is dervied from Jitterbugging, a mathematical transformation with a more technical name if you're a math snob (I can be).
#
#  # In[5]:
two * sqrt2 * (Ø**-2)
# In[6]:
icosa = five * sqrt2 * Ø ** 2
icosa
# In[7]:
ve = Decimal(20)
# In[8]:
s_factor = ve / icosa
# In[9]:
s_factor # see?
# ## "SMALLGUY"
#
# Above is an expression for the volume of said Icosa in tetravolumes.
#
# We may think of it as "two applications of the S-Factor bigger" than a smaller cubocta, with edges, get this, equal in magnitude to the *volume* of the edge 2 icosa.
#
# David Koski and I got to calling this cubocta "SmallGuy" (feel free to substitute your own moniker).
#
# The Concentric Hierarchy has a *Sesame Street* flavor (kids' TV show) in some walkx of life, lending to our penchant for colloquialisms.
# In[10]:
SmallGuy = icosa * one/s_factor * one/s_factor
SmallGuy
# Another way to reach the SmallGuy is to start with the volume 20 cubocta and shrink its edges by the S Factor, which means volume shrinks by a factor of the reciprocal of said S Factor to the 3rd power or $1/s\_factor ^{3}$
# In[11]:
ve * (one/s_factor)**3
# In[12]:
SmallGuy_edge = two * (one/s_factor) # effect on edges
SmallGuy_edge
# ## RHOMBIC TRIACONTAHEDRON (RT)
#
#
# In[5]:
two * sqrt2 * (Ø**-2)
# In[6]:
icosa = five * sqrt2 * Ø ** 2
icosa
# In[7]:
ve = Decimal(20)
# In[8]:
s_factor = ve / icosa
# In[9]:
s_factor # see?
# ## "SMALLGUY"
#
# Above is an expression for the volume of said Icosa in tetravolumes.
#
# We may think of it as "two applications of the S-Factor bigger" than a smaller cubocta, with edges, get this, equal in magnitude to the *volume* of the edge 2 icosa.
#
# David Koski and I got to calling this cubocta "SmallGuy" (feel free to substitute your own moniker).
#
# The Concentric Hierarchy has a *Sesame Street* flavor (kids' TV show) in some walkx of life, lending to our penchant for colloquialisms.
# In[10]:
SmallGuy = icosa * one/s_factor * one/s_factor
SmallGuy
# Another way to reach the SmallGuy is to start with the volume 20 cubocta and shrink its edges by the S Factor, which means volume shrinks by a factor of the reciprocal of said S Factor to the 3rd power or $1/s\_factor ^{3}$
# In[11]:
ve * (one/s_factor)**3
# In[12]:
SmallGuy_edge = two * (one/s_factor) # effect on edges
SmallGuy_edge
# ## RHOMBIC TRIACONTAHEDRON (RT)
#
#  # In[13]:
superRT = ve * S3
superRT
# S3 is our conversion constant for going between XYZ cube volumes and [IVM](https://github.com/4dsolutions/Python5/blob/master/Generating%20the%20FCC.ipynb) tetra volumes. The two mensuration systems each have their own unit volume, by convention a .5 radius edge cube versus a 1.0 diametered edged tetrahedron, or use edges 1 and 2 if preferred, their ratio will be the same, with the cube a bit bigger.
#
#
# In[13]:
superRT = ve * S3
superRT
# S3 is our conversion constant for going between XYZ cube volumes and [IVM](https://github.com/4dsolutions/Python5/blob/master/Generating%20the%20FCC.ipynb) tetra volumes. The two mensuration systems each have their own unit volume, by convention a .5 radius edge cube versus a 1.0 diametered edged tetrahedron, or use edges 1 and 2 if preferred, their ratio will be the same, with the cube a bit bigger.
#
#  #
# SuperRT is the RT (rhombic triacontahedron) formed by the Icosa and its dual, the Pentagonal Dodecahedron, the two five-fold symmetric shapes in [the Platonic set](https://youtu.be/vk-cpknOz9E) of five polys. The Icosa we're talking about is the one above, derived from the VE of volume 20, through Jitterbugging.
#
# If we shrink SuperRT down by $\phi^{-3}$ volume-wise (all edges are now $\phi^{-1}$ their initial length), and carve it into 120 modules (60 left, 60 right), then lo and behold, we have the E modules.
#
# Another expression for SuperRT volume is $15\sqrt{2}$.
# In[14]:
Decimal('15') * sqrt2
# ## E MODULE
#
#
#
# SuperRT is the RT (rhombic triacontahedron) formed by the Icosa and its dual, the Pentagonal Dodecahedron, the two five-fold symmetric shapes in [the Platonic set](https://youtu.be/vk-cpknOz9E) of five polys. The Icosa we're talking about is the one above, derived from the VE of volume 20, through Jitterbugging.
#
# If we shrink SuperRT down by $\phi^{-3}$ volume-wise (all edges are now $\phi^{-1}$ their initial length), and carve it into 120 modules (60 left, 60 right), then lo and behold, we have the E modules.
#
# Another expression for SuperRT volume is $15\sqrt{2}$.
# In[14]:
Decimal('15') * sqrt2
# ## E MODULE
#
#  # In[15]:
emod = (superRT * Ø**-3)/Decimal(120)
# In[16]:
emod
# In[17]:
smod = emod * s_factor
smod
# In[18]:
smod/emod
# The S factor again, yes?
#
# $\sqrt{2}-(\sqrt{2}(\phi^{-3}))= 2\sqrt{2}(\phi^{-2})$ = S Factor.
#
# Another expression for the S Factor is $24E + 8e3$ where E means emod, and $e3$ means $E * \phi^{-3}$.
# In[19]:
Decimal(24) * emod + Decimal(8) * emod * Ø**-3
# ## S MODULE
#
# Now lets shrink the 20 volumed VE by halving all edges, reducing volume by a factor of 8, to 2.5
#
# In[20]:
small_ve = ve / Decimal(8)
#
# In[15]:
emod = (superRT * Ø**-3)/Decimal(120)
# In[16]:
emod
# In[17]:
smod = emod * s_factor
smod
# In[18]:
smod/emod
# The S factor again, yes?
#
# $\sqrt{2}-(\sqrt{2}(\phi^{-3}))= 2\sqrt{2}(\phi^{-2})$ = S Factor.
#
# Another expression for the S Factor is $24E + 8e3$ where E means emod, and $e3$ means $E * \phi^{-3}$.
# In[19]:
Decimal(24) * emod + Decimal(8) * emod * Ø**-3
# ## S MODULE
#
# Now lets shrink the 20 volumed VE by halving all edges, reducing volume by a factor of 8, to 2.5
#
# In[20]:
small_ve = ve / Decimal(8)
#  #
# As every grade schooler knows, if at all aware of their heritage, said VE inscribes inside the octahedron of volume 4, as does an Icosahedron with flush faces. We do a kind of jitterbugging that makes the VE larger instead of smaller. Two applications of the S Factor does the trick.
# In[21]:
skew_icosa = small_ve * s_factor * s_factor
# In[22]:
skew_icosa
# In[23]:
skew_icosa + (24 * smod)
# The figure below is an S-Factor radius, meaning from the center to each diamond face center on the surface.
#
#
#
# As every grade schooler knows, if at all aware of their heritage, said VE inscribes inside the octahedron of volume 4, as does an Icosahedron with flush faces. We do a kind of jitterbugging that makes the VE larger instead of smaller. Two applications of the S Factor does the trick.
# In[21]:
skew_icosa = small_ve * s_factor * s_factor
# In[22]:
skew_icosa
# In[23]:
skew_icosa + (24 * smod)
# The figure below is an S-Factor radius, meaning from the center to each diamond face center on the surface.
#
#  #
#  #
#
#
#