#!/usr/bin/env python
# coding: utf-8

# # The E-module in Tetravolumes
# #### by D. Koski & K. Urner, June 2018
# 
# The E-module has long been a standard module, starting with Synergetics and persisting through the writings and research of several students of polyhedral dissections.
# 
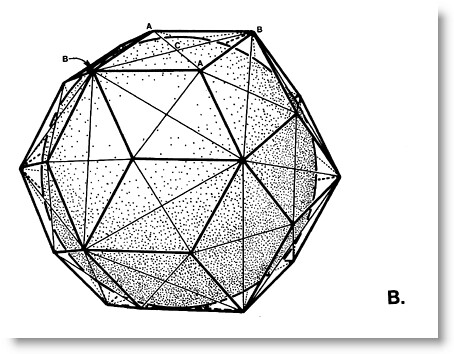
# The E is 1/120th of the Rhombic Triacontahedron with:
# 
# * radius = 1 (from center to surface face center)
# * surface face diagonals of 1/Ø and (1/Ø)(1/Ø)
# 
# In Synergetics, our unit of volume is the regular tetrahedron of edges D, where D is the diameter of a CCP sphere in densest packing, with twelve-around-one at any interior vertex or node.  D may be set at 1 or 2, in which case R (radius) will be 0.5 or 1 respectively.
# 
# <a data-flickr-embed="true"  href="https://www.flickr.com/photos/kirbyurner/4148457444/in/album-72157622797118549/" title="Rhombic Triacontahedron"><img src="https://farm3.staticflickr.com/2662/4148457444_60e88eee55.jpg" width="454" height="354" alt="Rhombic Triacontahedron"></a><script async src="//embedr.flickr.com/assets/client-code.js" charset="utf-8"></script>
# 
# <div align="center"><b>Fig 1. RT in Synergetics (Fig. 986.419)</b></div>
# 
# The E-mod's volume, in tetra-volumes, is: (√2/8)/ØØØ
# 
# The E-mod's volume is a little bigger than 1/24, the T-mod's volume i.e. 1/120th of a RT of volume 5 exactly.  Ts and Es come in left and right handed flavors.
# 
# The E-mods RT, scaled up by Ø in all linear dimensions, is the "child" of the Concentric Hierarchy Icosahedron of volume ~18.51 and its dual, the Pentagonal Dodecahedron.  When their edges cross, the thirty diamond-face mid-points are established, along with the corresponding vertexes.
# 
# When the RT is scaled up by Ø in all linear dimensions, volume goes up as a factor of Ø to the third power (we do *not* feel compelled to say "cubed" given the shape in question). David's notation for the larger Emod shapes is [E3](https://github.com/4dsolutions/Python5/blob/master/CuboidalE3.ipynb), whereas if we shrink Emod down by Ø in all linear dimensions, we call it e3 (lowercase means "smaller than"), e6 etc.  Ditto for the Smod.
# 
# For more on how the Platonics "give birth" to our Concentric Hierarchy players, check out [Genesis Story](https://youtu.be/vk-cpknOz9E) on Youtube.

# In[1]:


import tetravolume
Ø = (1 + 5**0.5)/2
from math import sqrt
Emod = sqrt(2)/8 * Ø**-3
Emod


# ![Koski tet](emod.jpg)
# 
# <div align="center"><b>Fig 2. Emod by D. Koski</b></div>
# 
# 
# The E mod tetravolume is (√2/8)/ØØØ or .041731  
# 
# In the figure above the E mod is further subdivided by additional intersecting planes creating what we might call Phe, Phi, Pho, Phum submodules.  This [subdivision of the E](https://github.com/4dsolutions/Python5/blob/master/BeanStalkSeries.ipynb) is discussed in more detail elsewhere.  The planes that cut the E3 per LCD trianges (derived from the 31 great circles of the spinning icosahedron), define a way to cut an E lying sideways on the E3's external face.
# 
# The E module proper, as depicted, has three blue orthogonal lengths: 
# * short_face_diag = 1/(Ø*Ø) = 0.381966
# * long_face_diag = 1/Ø = 0.618033 
# * radius = 1.000000
# 
# It then has 2 red lengths, serving as hypotenuses:
# * long_hypot = √(5-√5)/2 = 1.175570
# * short_hypot = √(5-2√5) = .726542
# 
# ... and finally, a yellow length, also an hypotenuse:
# * yellow = (Ø^-1)(√3) = 1.070466

# In[2]:


short_face_diag = 1/(Ø*Ø)
long_face_diag = 1/Ø
radius = 1.000000
long_hypot = sqrt((5-sqrt(5))/2)
short_hypot = sqrt(5-2*sqrt(5))
yellow = sqrt(3)/Ø


# Below, we convert these to Python and feed them to our volume computer, which sets D=1 i.e. our dimensions are twice as big (assuming R=1).  So the final step involves taking 1/8th the computed volume.

# In[3]:


print("Blue:")
print("   short_face_diag:", short_face_diag)
print("    long_face_diag:", long_face_diag)
print("            radius:", radius)
print("Red:")
print("        long_hypot:", long_hypot)
print("       short_hypot:", short_hypot)
print()
print("            yellow:", yellow)


# In[4]:


ivm_vol = tetravolume.Tetrahedron(radius, long_face_diag, short_face_diag,
                                 long_hypot, short_hypot, yellow).ivm_volume()
ivm_vol/8


# ![Koski tet](koski_tet.jpg)
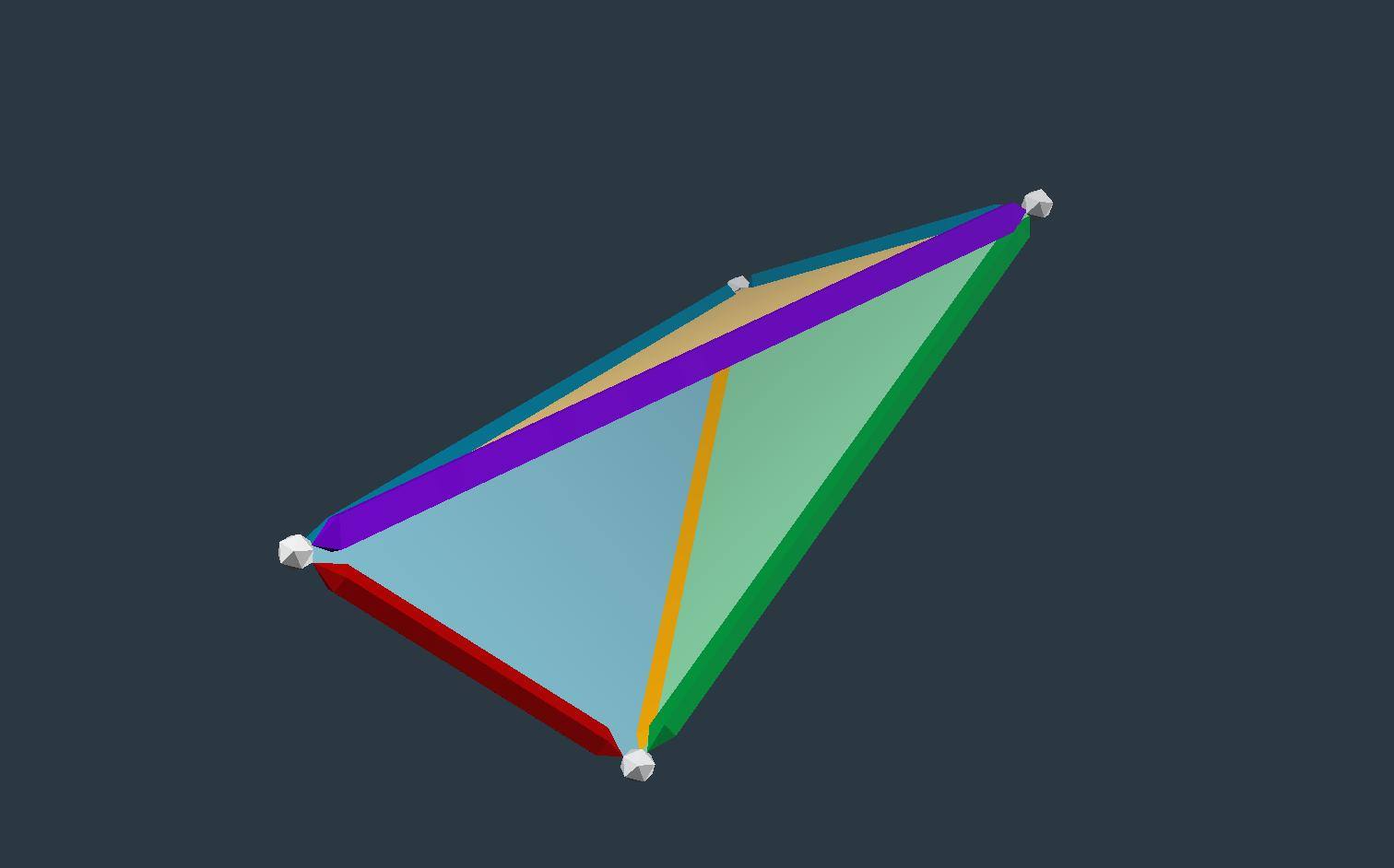
# <div align="center"><b>Fig 3. Same Volume as Emod, by D. Koski</b></div>
# 
# We may follow essentially the same workflow with this alternative tetrahedron which turns out to have the same volume as the E module.  Note the division by 8 in the final step.
# 
# * Short Blue = 1/Ø
# * Long Blue = 2/Ø
# * Yellow = √3/Ø
# * Purple = √3/Ø
# * Green = √2/Ø
# * Red = √((25-11√5)/2)

# In[5]:


purple = yellow = (3**0.5)/Ø
short_blue = 1/Ø
long_blue = 2/Ø
green = sqrt(2)/Ø
red = sqrt((25-11*sqrt(5))/2) 


# In[6]:


print("phi", Ø)
print("Purple, Yellow:", purple)
print("    Short Blue:", short_blue)
print("     Long Blue:", long_blue)
print("         Green:", green)
print("           Red:", red)


# In[7]:


ivm_vol = tetravolume.Tetrahedron(red, yellow, green, long_blue, short_blue, purple).ivm_volume()


# In[8]:


ivm_vol/8


# So far, we've depending on the built-in ```float``` type for our computations, but lets remember our 3rd party assets, in addition to ```decimal.Decimal``` in the Standard Library.
# 
# The computations below run through some of the same volumes already talked about, such as the E-module.

# In[9]:


import gmpy2

gmpy2.get_context().precision=300
Ø = (1 + gmpy2.root(5, 2))/2
vol_scale_factor = 1.5
rad_scale_factor = gmpy2.root(vol_scale_factor, 3)

h = (Ø / gmpy2.root(2,2)) * (1/rad_scale_factor)
print("RT5 radius: {:42.40f}".format(h))
S3 = gmpy2.root(9/8, 2)
SuperRT_vol = S3 * 20
print("SuperRT:   {:42.40f}".format( SuperRT_vol))
Emod_RT_vol = SuperRT_vol * (1/Ø)**3
print("5+ RT:      {:42.40f}".format( Emod_RT_vol ))
Tmod_RT_vol = gmpy2.mpfr(float(5.0))
print("5  RT:      {:42.40f}".format( Tmod_RT_vol ))
print("Emod:       {:42.40f}".format( Emod_RT_vol/120 ))
print("Tmod:       {:42.40f}".format( Tmod_RT_vol/120 ))