#!/usr/bin/env python
# coding: utf-8
# # Denoising Diffusion Probabilistic Model (DDPM)
#
# This notebook focuses on the implementation from scratch of DDPM [[1](https://proceedings.neurips.cc/paper/2020/file/4c5bcfec8584af0d967f1ab10179ca4b-Paper.pdf)] and is inspired by three great blogs: [[2](https://huggingface.co/blog/annotated-diffusion)], [[3](https://benanne.github.io/2022/05/26/guidance.html)], and [[10](https://lilianweng.github.io/posts/2021-07-11-diffusion-models/)]
# ## Setup
#
# Diffusion models roughly consist of two parts:
#
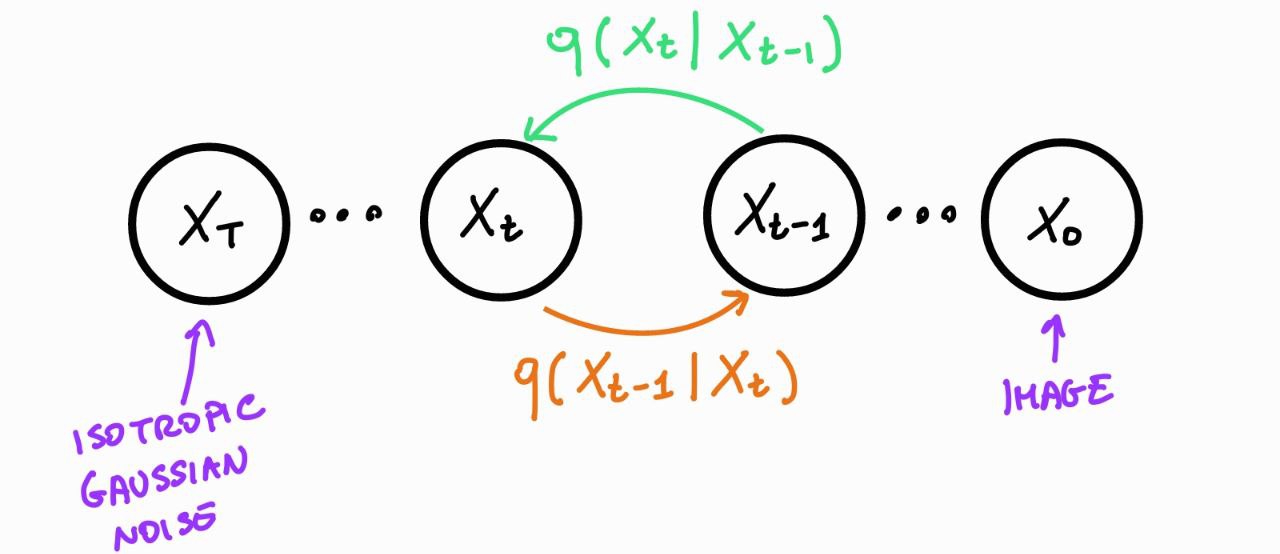
# - A predefined **forward** diffusion process $q(\boldsymbol{x}_t|\boldsymbol{x}_{t-1})$ of our choosing, that gradually adds Gaussian noise to an image until it becomes pure noise.
# - A **reverse** denoising diffusion process $q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$ , approximated by a neural network, which gradually denoises an image starting from pure noise.
#
#  # ### Forward process
#
# ### Forward process
# 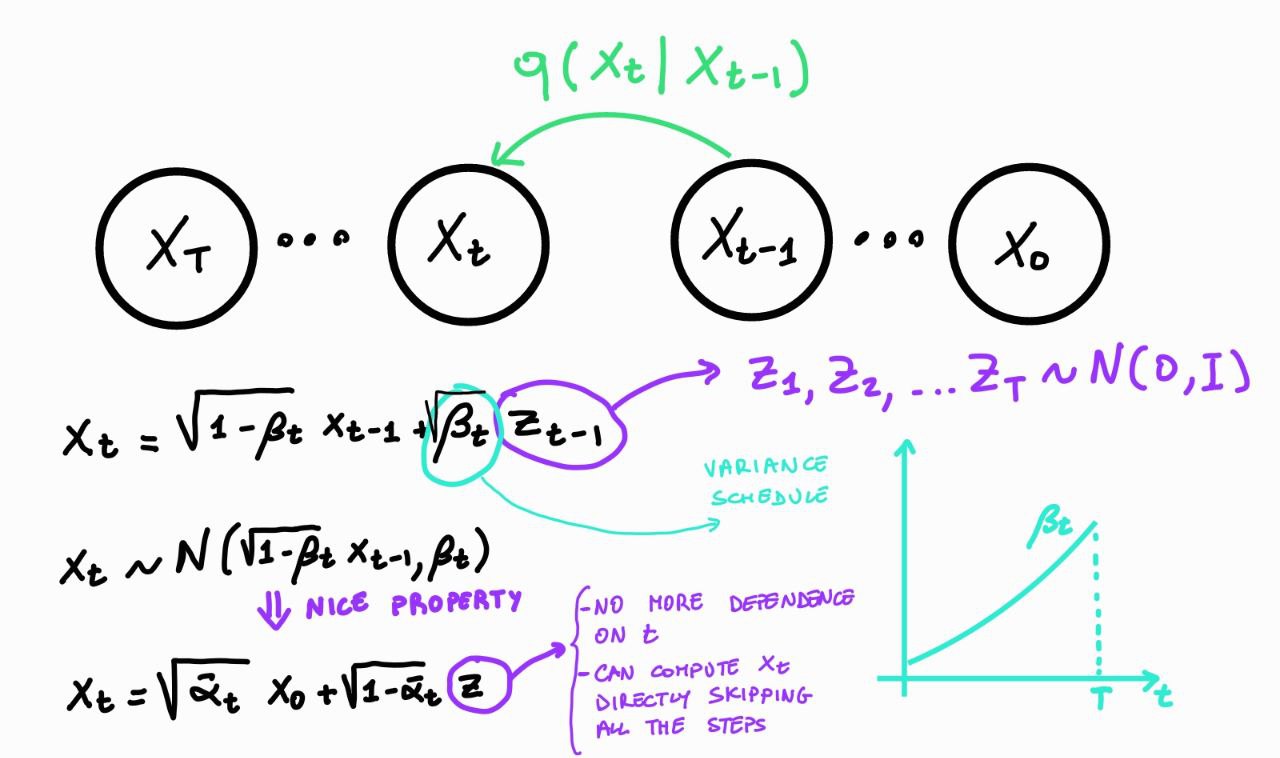 # **Nice property:** Let $\alpha_t = 1 - \beta_t$ and $\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$
#
# \begin{align}
# \boldsymbol{x}_t & = \sqrt{\alpha_t} \boldsymbol{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1} \;\;\; \text{where} \;\boldsymbol{z}_{t-1}, \boldsymbol{z}_{t-2}, \dots, \mathcal{N}(\mathbf{0}, \mathbf{I}).\\
# & = \sqrt{\alpha_t} \lbrack \sqrt{\alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{1- \alpha_{t-1}}\boldsymbol{z}_{t-2} \rbrack + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1}\\
# & = \sqrt{\alpha_t \alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}}\boldsymbol{z}_{t-2} + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1}\\
# & = \sqrt{\alpha_t \alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}}\boldsymbol{\bar{z}}_{t-2} \;\;\; \text{where} \; \boldsymbol{\bar{z}}_{t-2} \; \text{merges two Gaussians}^1 \\
# & = \dots \\
# & = \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\bar{z}_0} \;\;\; \text{where} \; \boldsymbol{\bar{z}_0} = \boldsymbol{z} \\
# q(\boldsymbol{x}_t|\boldsymbol{x}_0) & = \mathcal{N}(\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0, 1 - \bar{\alpha}_t)
# \end{align}
#
# $^1$ the sum of two Gaussian variables $\boldsymbol{z}_1 \sim \mathcal{N}(\mathbf{0}, \sigma_1^2 \mathbf{I})$ and $\boldsymbol{z}_2 \sim \mathcal{N}(\mathbf{0}, \sigma_2^2 \mathbf{I})$ is a new variable $\bar{\boldsymbol{z}} \sim \mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2) \mathbf{I})$. In our case, $\boldsymbol{z}_{t-1} \sim \mathcal{N}(\mathbf{0}, (1-\alpha_t) \mathbf{I})$ and $\boldsymbol{z}_{t-2} \sim \mathcal{N}(\mathbf{0}, (\alpha_t - \alpha_t \alpha_{t-1}) \mathbf{I})$, so $\boldsymbol{\bar{z}}_{t-2} \sim \mathcal{N}(\mathbf{0}, (1 - \alpha_t \alpha_{t-1}) \mathbf{I})$.
# In[1]:
import numpy as np
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
import torch
from torch import nn
import torch.nn.functional as F
import torchvision
# First, we define the scheduler to compute $\beta_t$. The simplest is the linear scheduler, but more advanced schedulers can give better results.
# In[2]:
def linear_beta_schedule(timesteps):
beta_start = 0.0001
beta_end = 0.02
return torch.linspace(beta_start, beta_end, timesteps)
# In[3]:
timesteps = 200
# compute betas
betas = linear_beta_schedule(timesteps=timesteps)
# compute alphas
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
# calculations for the forward diffusion q(x_t | x_{t-1})
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)
# Let's illustrate how noise is added to a sample image at each time step of the diffusion process.
# In[4]:
from PIL import Image
image = Image.open("img/lion_short.png")
image
# Next, we resize the image, rescale it in $[-1, 1]$, and convert it to a PyTorch tensor.
# In[5]:
from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize
image_size = 128
transform = Compose([
Resize(image_size),
ToTensor(), # turn into Numpy array of shape HWC, divide by 255
Lambda(lambda t: (t * 2) - 1), # [0,1] --> [-1,1]
])
x_start = transform(image).unsqueeze(0)
x_start.shape
# We also define the reverse transform, which maps a PyTorch tensor with in $[−1,1]$ back into a PIL image.
# In[6]:
reverse_transform = Compose([
Lambda(lambda t: (t + 1) / 2),
Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC
Lambda(lambda t: t * 255.),
Lambda(lambda t: t.numpy().astype(np.uint8)),
ToPILImage(),
])
reverse_transform(x_start.squeeze())
# We can now define the forward diffusion process.
# In[7]:
# utility function to extract the appropriate t index for a batch of indices.
# e.g., t=[10,11], x_shape=[b,c,h,w] --> a.shape = [2,1,1,1]
# e.g., t=[7,12,15,20], x_shape=[b,h,w] --> a.shape = [4,1,1]
def extract(a, t, x_shape):
batch_size = t.shape[0]
out = a.gather(-1, t.cpu())
return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)
# forward diffusion (using the nice property)
def q_sample(x_start, t, noise=None):
if noise is None:
noise = torch.randn_like(x_start) # z (it does not depend on t!)
# adjust the shape
sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x_start.shape
)
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
# Let's test on a specific time step, $t=20$:
# In[8]:
def get_noisy_image(x_start, t):
x_noisy = q_sample(x_start, t=t) # add noise
noisy_image = reverse_transform(x_noisy.squeeze()) # turn back into PIL image
return noisy_image
# In[9]:
t = torch.tensor([19])
get_noisy_image(x_start[0], t)
# In[10]:
def plot_seq(imgs, with_orig=False, row_title=None, **imshow_kwargs):
if not isinstance(imgs[0], list):
# Make a 2d grid even if there's just 1 row
imgs = [imgs]
num_rows = len(imgs)
num_cols = len(imgs[0]) + with_orig
fig, axs = plt.subplots(figsize=(200,200), nrows=num_rows, ncols=num_cols, squeeze=False)
for row_idx, row in enumerate(imgs):
row = [image] + row if with_orig else row
for col_idx, img in enumerate(row):
ax = axs[row_idx, col_idx]
ax.imshow(np.asarray(img), **imshow_kwargs)
ax.set(xticklabels=[], yticklabels=[], xticks=[], yticks=[])
if with_orig:
axs[0, 0].set(title='Original image')
axs[0, 0].title.set_size(8)
if row_title is not None:
for row_idx in range(num_rows):
axs[row_idx, 0].set(ylabel=row_title[row_idx])
plt.tight_layout()
# In[11]:
plot_seq([get_noisy_image(x_start, torch.tensor([t])) for t in [1, 50, 100, 150, 199]])
# ### Backward process
#
# **Nice property:** Let $\alpha_t = 1 - \beta_t$ and $\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$
#
# \begin{align}
# \boldsymbol{x}_t & = \sqrt{\alpha_t} \boldsymbol{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1} \;\;\; \text{where} \;\boldsymbol{z}_{t-1}, \boldsymbol{z}_{t-2}, \dots, \mathcal{N}(\mathbf{0}, \mathbf{I}).\\
# & = \sqrt{\alpha_t} \lbrack \sqrt{\alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{1- \alpha_{t-1}}\boldsymbol{z}_{t-2} \rbrack + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1}\\
# & = \sqrt{\alpha_t \alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}}\boldsymbol{z}_{t-2} + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1}\\
# & = \sqrt{\alpha_t \alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}}\boldsymbol{\bar{z}}_{t-2} \;\;\; \text{where} \; \boldsymbol{\bar{z}}_{t-2} \; \text{merges two Gaussians}^1 \\
# & = \dots \\
# & = \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\bar{z}_0} \;\;\; \text{where} \; \boldsymbol{\bar{z}_0} = \boldsymbol{z} \\
# q(\boldsymbol{x}_t|\boldsymbol{x}_0) & = \mathcal{N}(\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0, 1 - \bar{\alpha}_t)
# \end{align}
#
# $^1$ the sum of two Gaussian variables $\boldsymbol{z}_1 \sim \mathcal{N}(\mathbf{0}, \sigma_1^2 \mathbf{I})$ and $\boldsymbol{z}_2 \sim \mathcal{N}(\mathbf{0}, \sigma_2^2 \mathbf{I})$ is a new variable $\bar{\boldsymbol{z}} \sim \mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2) \mathbf{I})$. In our case, $\boldsymbol{z}_{t-1} \sim \mathcal{N}(\mathbf{0}, (1-\alpha_t) \mathbf{I})$ and $\boldsymbol{z}_{t-2} \sim \mathcal{N}(\mathbf{0}, (\alpha_t - \alpha_t \alpha_{t-1}) \mathbf{I})$, so $\boldsymbol{\bar{z}}_{t-2} \sim \mathcal{N}(\mathbf{0}, (1 - \alpha_t \alpha_{t-1}) \mathbf{I})$.
# In[1]:
import numpy as np
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
import torch
from torch import nn
import torch.nn.functional as F
import torchvision
# First, we define the scheduler to compute $\beta_t$. The simplest is the linear scheduler, but more advanced schedulers can give better results.
# In[2]:
def linear_beta_schedule(timesteps):
beta_start = 0.0001
beta_end = 0.02
return torch.linspace(beta_start, beta_end, timesteps)
# In[3]:
timesteps = 200
# compute betas
betas = linear_beta_schedule(timesteps=timesteps)
# compute alphas
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
# calculations for the forward diffusion q(x_t | x_{t-1})
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)
# Let's illustrate how noise is added to a sample image at each time step of the diffusion process.
# In[4]:
from PIL import Image
image = Image.open("img/lion_short.png")
image
# Next, we resize the image, rescale it in $[-1, 1]$, and convert it to a PyTorch tensor.
# In[5]:
from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize
image_size = 128
transform = Compose([
Resize(image_size),
ToTensor(), # turn into Numpy array of shape HWC, divide by 255
Lambda(lambda t: (t * 2) - 1), # [0,1] --> [-1,1]
])
x_start = transform(image).unsqueeze(0)
x_start.shape
# We also define the reverse transform, which maps a PyTorch tensor with in $[−1,1]$ back into a PIL image.
# In[6]:
reverse_transform = Compose([
Lambda(lambda t: (t + 1) / 2),
Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC
Lambda(lambda t: t * 255.),
Lambda(lambda t: t.numpy().astype(np.uint8)),
ToPILImage(),
])
reverse_transform(x_start.squeeze())
# We can now define the forward diffusion process.
# In[7]:
# utility function to extract the appropriate t index for a batch of indices.
# e.g., t=[10,11], x_shape=[b,c,h,w] --> a.shape = [2,1,1,1]
# e.g., t=[7,12,15,20], x_shape=[b,h,w] --> a.shape = [4,1,1]
def extract(a, t, x_shape):
batch_size = t.shape[0]
out = a.gather(-1, t.cpu())
return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)
# forward diffusion (using the nice property)
def q_sample(x_start, t, noise=None):
if noise is None:
noise = torch.randn_like(x_start) # z (it does not depend on t!)
# adjust the shape
sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x_start.shape
)
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
# Let's test on a specific time step, $t=20$:
# In[8]:
def get_noisy_image(x_start, t):
x_noisy = q_sample(x_start, t=t) # add noise
noisy_image = reverse_transform(x_noisy.squeeze()) # turn back into PIL image
return noisy_image
# In[9]:
t = torch.tensor([19])
get_noisy_image(x_start[0], t)
# In[10]:
def plot_seq(imgs, with_orig=False, row_title=None, **imshow_kwargs):
if not isinstance(imgs[0], list):
# Make a 2d grid even if there's just 1 row
imgs = [imgs]
num_rows = len(imgs)
num_cols = len(imgs[0]) + with_orig
fig, axs = plt.subplots(figsize=(200,200), nrows=num_rows, ncols=num_cols, squeeze=False)
for row_idx, row in enumerate(imgs):
row = [image] + row if with_orig else row
for col_idx, img in enumerate(row):
ax = axs[row_idx, col_idx]
ax.imshow(np.asarray(img), **imshow_kwargs)
ax.set(xticklabels=[], yticklabels=[], xticks=[], yticks=[])
if with_orig:
axs[0, 0].set(title='Original image')
axs[0, 0].title.set_size(8)
if row_title is not None:
for row_idx in range(num_rows):
axs[row_idx, 0].set(ylabel=row_title[row_idx])
plt.tight_layout()
# In[11]:
plot_seq([get_noisy_image(x_start, torch.tensor([t])) for t in [1, 50, 100, 150, 199]])
# ### Backward process
# 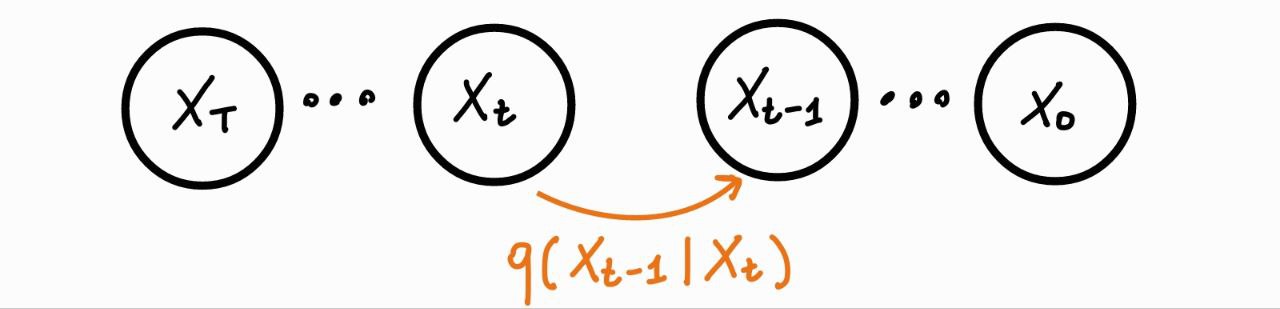 #
# - If $\beta_t$ is small enough, $q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$ will be a Gaussian $\mathcal{N}\big(\tilde{\mu}(\boldsymbol{x}_t), \tilde{\sigma}(\boldsymbol{x}_t)\big)$
# - However, we cannot compute $\tilde{\mu}(\boldsymbol{x}_t)$ and $\tilde{\sigma}(\boldsymbol{x}_t)$ analytically, because requires knowing the true data distribution $p(\boldsymbol{x})$
# $$ q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)q(\boldsymbol{x}_{t-2}|\boldsymbol{x}_{t-1})\dots \rightarrow p(\boldsymbol{x}_0)$$
# - We can use a NN to learn $\tilde{\mu}(\boldsymbol{x}_t)$ and $\tilde{\sigma}(\boldsymbol{x}_t)$
# ### Simplification
#
# Represent $\tilde{\sigma}(\boldsymbol{x}_t)$ with a time dependent constant $\tilde{\beta}_t$
#
# ### Manipulation
#
# Condition on $\boldsymbol{x}_0$ and obtain
# $q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t$ ,
# $\boldsymbol{x}_0$
# $)$
# $ = \mathcal{N} \big( $
# $\tilde{\mu}(\boldsymbol{x}_t, \boldsymbol{x}_0)$ ,
# $\tilde{\beta}_t$
# $\big) = \mathcal{N} \big( $
# $\tilde{\mu}_t$ ,
# $\tilde{\beta}_t$
# $\big)$
#
# where
#
#
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
#
# and
#
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
#
#
# - If $\beta_t$ is small enough, $q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$ will be a Gaussian $\mathcal{N}\big(\tilde{\mu}(\boldsymbol{x}_t), \tilde{\sigma}(\boldsymbol{x}_t)\big)$
# - However, we cannot compute $\tilde{\mu}(\boldsymbol{x}_t)$ and $\tilde{\sigma}(\boldsymbol{x}_t)$ analytically, because requires knowing the true data distribution $p(\boldsymbol{x})$
# $$ q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)q(\boldsymbol{x}_{t-2}|\boldsymbol{x}_{t-1})\dots \rightarrow p(\boldsymbol{x}_0)$$
# - We can use a NN to learn $\tilde{\mu}(\boldsymbol{x}_t)$ and $\tilde{\sigma}(\boldsymbol{x}_t)$
# ### Simplification
#
# Represent $\tilde{\sigma}(\boldsymbol{x}_t)$ with a time dependent constant $\tilde{\beta}_t$
#
# ### Manipulation
#
# Condition on $\boldsymbol{x}_0$ and obtain
# $q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t$ ,
# $\boldsymbol{x}_0$
# $)$
# $ = \mathcal{N} \big( $
# $\tilde{\mu}(\boldsymbol{x}_t, \boldsymbol{x}_0)$ ,
# $\tilde{\beta}_t$
# $\big) = \mathcal{N} \big( $
# $\tilde{\mu}_t$ ,
# $\tilde{\beta}_t$
# $\big)$
#
# where
#
#
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
#
# and
#
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
#  # ### NN Model
#
# - Take a look at
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
# and
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
# - The only thing we do not know is $\boldsymbol{\tilde z}_t$ .
# - We approximate $\boldsymbol{\tilde z}_t$ with a NN.
#
#
#
# ### NN Model
#
# - Take a look at
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
# and
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
# - The only thing we do not know is $\boldsymbol{\tilde z}_t$ .
# - We approximate $\boldsymbol{\tilde z}_t$ with a NN.
#
#
# 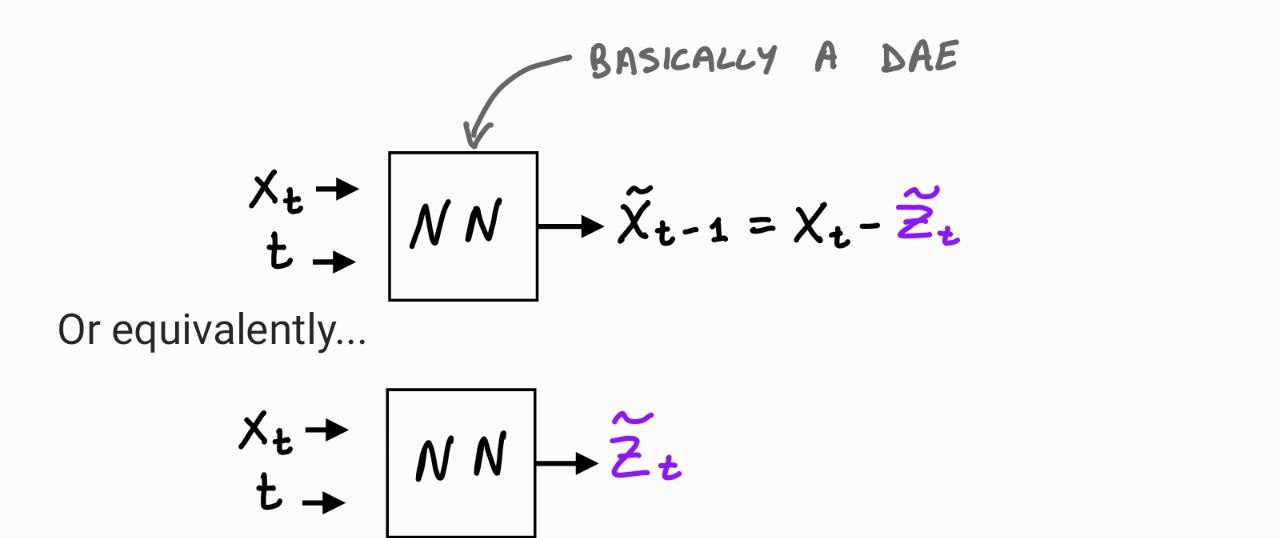 #
# As NN, we use a Unet.
# 
# In[12]:
# Let's look at how the time embeddings look like
from scripts.unet import SinusoidalPositionEmbeddings
time_emb = SinusoidalPositionEmbeddings(100)
t1 = time_emb(torch.tensor([10]))
t2 = time_emb(torch.tensor([12]))
t3 = time_emb(torch.tensor([30]))
fig, ax = plt.subplots(figsize=(5,3))
ax.plot(t1.numpy()[0], label='t=10')
ax.plot(t2.numpy()[0], label='t=12')
ax.plot(t3.numpy()[0], label='t=30')
plt.legend();
# In[13]:
# Let's check the input and output of the U-net
from scripts.unet import Unet
temp_model = Unet(
dim=image_size,
channels=3,
dim_mults=(1, 2, 4,)
)
with torch.no_grad():
out = temp_model(x_start, torch.tensor([40]))
print(f"input shape: {x_start.shape}, output shape: { out.shape}")
# ### Loss
#
#
#
# As NN, we use a Unet.
# 
# In[12]:
# Let's look at how the time embeddings look like
from scripts.unet import SinusoidalPositionEmbeddings
time_emb = SinusoidalPositionEmbeddings(100)
t1 = time_emb(torch.tensor([10]))
t2 = time_emb(torch.tensor([12]))
t3 = time_emb(torch.tensor([30]))
fig, ax = plt.subplots(figsize=(5,3))
ax.plot(t1.numpy()[0], label='t=10')
ax.plot(t2.numpy()[0], label='t=12')
ax.plot(t3.numpy()[0], label='t=30')
plt.legend();
# In[13]:
# Let's check the input and output of the U-net
from scripts.unet import Unet
temp_model = Unet(
dim=image_size,
channels=3,
dim_mults=(1, 2, 4,)
)
with torch.no_grad():
out = temp_model(x_start, torch.tensor([40]))
print(f"input shape: {x_start.shape}, output shape: { out.shape}")
# ### Loss
#
#  #
#
#
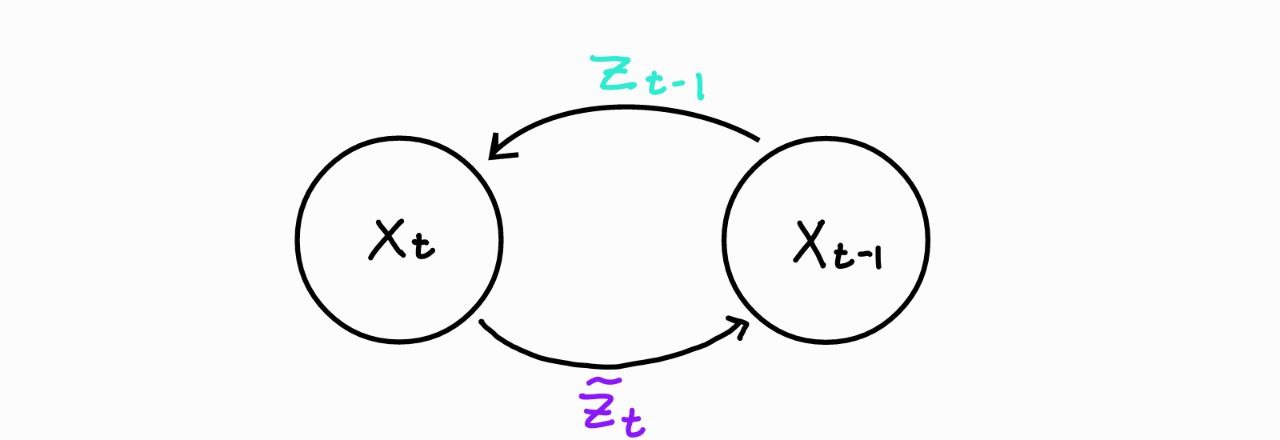
# - Loss: $ \| $ $\boldsymbol{ z}_{t-1}$ - $\boldsymbol{\tilde z}_{t}$ $\|_1 = \| $ $\boldsymbol{ z}_{t-1}$ - NN$(\boldsymbol{x}_t, t)$ $\|_1$
# - $\boldsymbol{ z}_{t-1}$ is the noise used to compute $\boldsymbol{x}_t$ in the forward process
# - Remember that to compute $\boldsymbol{x}_t$ we dropped the time index on $\boldsymbol{z}$ (nice property):
# $$ \boldsymbol{x}_t = \sqrt{\bar \alpha_t} \boldsymbol{x}_0 + \sqrt{1 - \bar \alpha_t} \boldsymbol{z} $$
# - Simply, we can sample $\boldsymbol{z}$ , compute $\boldsymbol{x}_t$, and recover $\boldsymbol{z}$ with the $NN$
# ### Training
#
#
#
#
#
# - Loss: $ \| $ $\boldsymbol{ z}_{t-1}$ - $\boldsymbol{\tilde z}_{t}$ $\|_1 = \| $ $\boldsymbol{ z}_{t-1}$ - NN$(\boldsymbol{x}_t, t)$ $\|_1$
# - $\boldsymbol{ z}_{t-1}$ is the noise used to compute $\boldsymbol{x}_t$ in the forward process
# - Remember that to compute $\boldsymbol{x}_t$ we dropped the time index on $\boldsymbol{z}$ (nice property):
# $$ \boldsymbol{x}_t = \sqrt{\bar \alpha_t} \boldsymbol{x}_0 + \sqrt{1 - \bar \alpha_t} \boldsymbol{z} $$
# - Simply, we can sample $\boldsymbol{z}$ , compute $\boldsymbol{x}_t$, and recover $\boldsymbol{z}$ with the $NN$
# ### Training
#
# 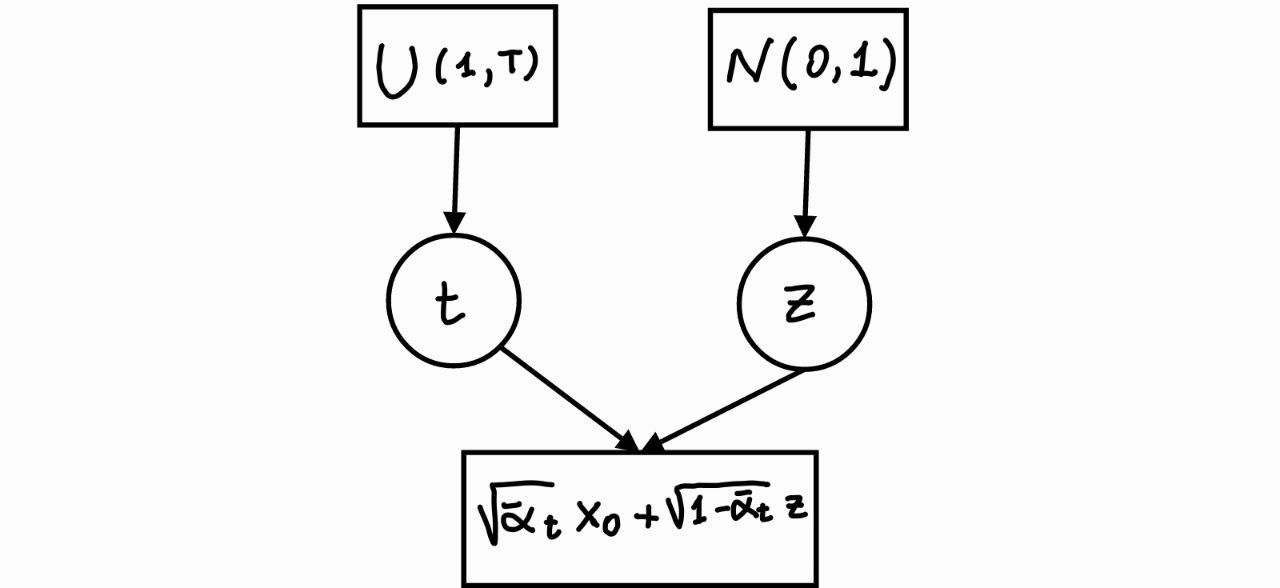 #
# **repeat**
# - Sample an image from the training data
# - $\boldsymbol{x}_0 \sim p(\boldsymbol{x}_0)$
# - Sample $\boldsymbol{ z}$ and $t$ randomly
# - $t \sim \mathcal{U}([1, T])$
# - $\boldsymbol{ z}$ $\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$
# - Take gradient descent step on
# $ \nabla_\theta \|$
# $\boldsymbol{ z}$ -
#
# NN$( \sqrt{\bar \alpha_t} \boldsymbol{x}_0 + \sqrt{1 - \bar \alpha_t}$
#
#
# $\boldsymbol{z}$
#
#
# $)$
#
# $\|_1 $
#
# **until** converged
# In[14]:
def p_losses(denoise_model, x_start, t, loss_type="huber"):
# random sample z
noise = torch.randn_like(x_start)
# compute x_t
x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
# recover z from x_t with the NN
predicted_noise = denoise_model(x_noisy, t)
if loss_type == 'l1':
loss = F.l1_loss(noise, predicted_noise)
elif loss_type == 'l2':
loss = F.mse_loss(noise, predicted_noise)
elif loss_type == "huber":
loss = F.smooth_l1_loss(noise, predicted_noise)
else:
raise NotImplementedError()
return loss
# ### Sampling
#
# We said that
# $\boldsymbol{x}_{t-1} \sim \mathcal{N} \big( $
# $\tilde{\mu}_t$ ,
# $\tilde{\beta}_t$
# $\big)$
# where
#
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
# and
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
#
#
#
# **repeat**
# - Sample an image from the training data
# - $\boldsymbol{x}_0 \sim p(\boldsymbol{x}_0)$
# - Sample $\boldsymbol{ z}$ and $t$ randomly
# - $t \sim \mathcal{U}([1, T])$
# - $\boldsymbol{ z}$ $\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$
# - Take gradient descent step on
# $ \nabla_\theta \|$
# $\boldsymbol{ z}$ -
#
# NN$( \sqrt{\bar \alpha_t} \boldsymbol{x}_0 + \sqrt{1 - \bar \alpha_t}$
#
#
# $\boldsymbol{z}$
#
#
# $)$
#
# $\|_1 $
#
# **until** converged
# In[14]:
def p_losses(denoise_model, x_start, t, loss_type="huber"):
# random sample z
noise = torch.randn_like(x_start)
# compute x_t
x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
# recover z from x_t with the NN
predicted_noise = denoise_model(x_noisy, t)
if loss_type == 'l1':
loss = F.l1_loss(noise, predicted_noise)
elif loss_type == 'l2':
loss = F.mse_loss(noise, predicted_noise)
elif loss_type == "huber":
loss = F.smooth_l1_loss(noise, predicted_noise)
else:
raise NotImplementedError()
return loss
# ### Sampling
#
# We said that
# $\boldsymbol{x}_{t-1} \sim \mathcal{N} \big( $
# $\tilde{\mu}_t$ ,
# $\tilde{\beta}_t$
# $\big)$
# where
#
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
# and
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
#
# 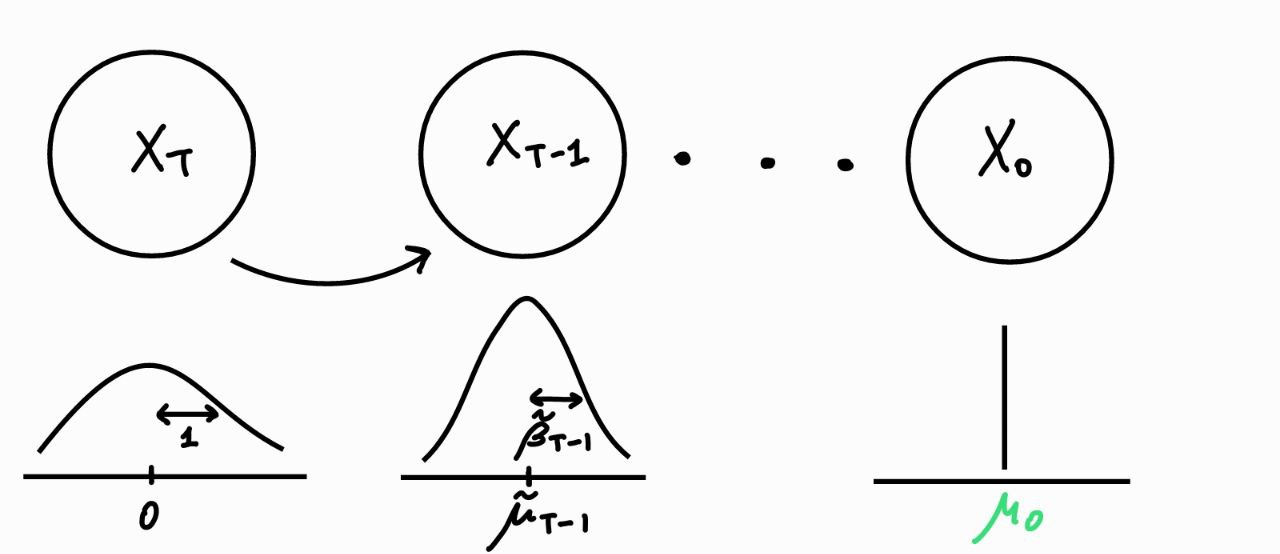 # #### *Sampling algorithm*
# $\boldsymbol{x}_T \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$
#
# **for** $t=T-1, \dots, 0$ **do**
# - $\boldsymbol{z} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ if $t > 1$ else $\boldsymbol{z}=0$
# - $\boldsymbol{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \big( \boldsymbol{x}_{t} - \frac{\beta_t}{\sqrt{1 - \bar{ \alpha}_t}}$ NN$(\boldsymbol{x}_t, t)$ $\big) + \tilde \beta_t \boldsymbol{z}$
#
# **return** $\boldsymbol{x}_{0} = \mu_0$
# In[16]:
# calculations for posterior q(x_{t-1} | x_t, x_0) = q(x_{t-1} | t, x_0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod) # β_t
@torch.no_grad()
def p_sample(model, x, t, t_index):
# adjust shapes
betas_t = extract(betas, t, x.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x.shape
)
sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
# Use the NN to predict the mean
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t)
# Draw the next sample
if t_index == 0:
return model_mean
else:
posterior_variance_t = extract(posterior_variance, t, x.shape) # beta_t
noise = torch.randn_like(x) # z
return model_mean + torch.sqrt(posterior_variance_t) * noise # x_{t-1}
# In[17]:
# Sampling loop
@torch.no_grad()
def p_sample_loop(model, shape):
device = next(model.parameters()).device
# start from pure noise (for each example in the batch)
img = torch.randn(shape, device=device)
imgs = []
for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
img = p_sample(model, img, torch.full((shape[0],), i, device=device, dtype=torch.long), i)
imgs.append(img)
return imgs
@torch.no_grad()
def sample(model, image_size, batch_size=16, channels=3):
return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))
# ### Train the model on Fashion MNIST
#
#
# #### *Sampling algorithm*
# $\boldsymbol{x}_T \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$
#
# **for** $t=T-1, \dots, 0$ **do**
# - $\boldsymbol{z} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ if $t > 1$ else $\boldsymbol{z}=0$
# - $\boldsymbol{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \big( \boldsymbol{x}_{t} - \frac{\beta_t}{\sqrt{1 - \bar{ \alpha}_t}}$ NN$(\boldsymbol{x}_t, t)$ $\big) + \tilde \beta_t \boldsymbol{z}$
#
# **return** $\boldsymbol{x}_{0} = \mu_0$
# In[16]:
# calculations for posterior q(x_{t-1} | x_t, x_0) = q(x_{t-1} | t, x_0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod) # β_t
@torch.no_grad()
def p_sample(model, x, t, t_index):
# adjust shapes
betas_t = extract(betas, t, x.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x.shape
)
sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
# Use the NN to predict the mean
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t)
# Draw the next sample
if t_index == 0:
return model_mean
else:
posterior_variance_t = extract(posterior_variance, t, x.shape) # beta_t
noise = torch.randn_like(x) # z
return model_mean + torch.sqrt(posterior_variance_t) * noise # x_{t-1}
# In[17]:
# Sampling loop
@torch.no_grad()
def p_sample_loop(model, shape):
device = next(model.parameters()).device
# start from pure noise (for each example in the batch)
img = torch.randn(shape, device=device)
imgs = []
for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
img = p_sample(model, img, torch.full((shape[0],), i, device=device, dtype=torch.long), i)
imgs.append(img)
return imgs
@torch.no_grad()
def sample(model, image_size, batch_size=16, channels=3):
return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))
# ### Train the model on Fashion MNIST
#
#  # In[18]:
from datasets import load_dataset
dataset = load_dataset("fashion_mnist")
image_size = 28
channels = 1
batch_size = 128
# Next, we define some basic image preprocessing on-the-fly: random horizontal flips, converstion to tensor, and rescaling in the $[-1,1]$ range.
#
# We use ``with_transform`` to apply the transformations to the elements in the dataset.
# In[19]:
from torchvision import transforms
from torch.utils.data import DataLoader
# define image transformations (e.g. using torchvision)
transform = Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Lambda(lambda t: (t * 2) - 1)
])
# define function
def transforms(examples):
examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]]
del examples["image"]
return examples
transformed_dataset = dataset.with_transform(transforms).remove_columns("label")
# create dataloader
dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)
# In[20]:
from torch.optim import Adam
device = "cuda" if torch.cuda.is_available() else "cpu"
model = Unet(
dim=image_size,
channels=channels,
dim_mults=(1, 2, 4,)
)
model.to(device)
optimizer = Adam(model.parameters(), lr=1e-3)
# In[21]:
from torchvision.utils import save_image
epochs = 10
for epoch in range(epochs):
for step, batch in enumerate(dataloader):
optimizer.zero_grad()
# x0
batch_size = batch["pixel_values"].shape[0]
batch = batch["pixel_values"].to(device)
# sample t from U(0,T)
t = torch.randint(0, timesteps, (batch_size,), device=device).long()
loss = p_losses(model, batch, t)
if step % 100 == 0:
print(f"Epoch: {epoch}, step: {step} -- Loss: {loss.item():.3f}")
loss.backward()
optimizer.step()
# ### Inference
#
# Once trained, we can sample from the model using ``sample`` the function defined above:
# In[22]:
# Generate 64 images
samples = sample(model, image_size=image_size, batch_size=64, channels=channels)
# Get the last sample and normalize it in [0,1]
last_sample = (samples[-1] - samples[-1].min())/(samples[-1].max()-samples[-1].min())
grid_img = torchvision.utils.make_grid(last_sample, nrow=16)
get_ipython().run_line_magic('matplotlib', 'inline')
plt.figure(figsize = (20,10))
plt.imshow(grid_img.permute(1, 2, 0).cpu().numpy(), cmap='gray');
# Visualize the actual denoising process with an animation
# In[25]:
import matplotlib.animation as animation
get_ipython().run_line_magic('matplotlib', 'notebook')
random_index = 6
fig = plt.figure()
ims = []
for i in range(timesteps):
im = plt.imshow(samples[i][random_index].cpu().numpy().reshape(image_size, image_size, channels), cmap="gray", animated=True)
ims.append([im])
animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)
animate.save('diffusion.gif')
plt.show()
# ## Next steps
#
# - Sample generation can be conditioned on inputs such as text (text2img) and images (img2img) [[4](https://arxiv.org/abs/2204.06125)].
# - Besides the mean, learning the standard deviation $\tilde{\sigma}(\boldsymbol{x}_t)$ of the conditional distribution helps in improving performance [[5](https://arxiv.org/abs/2102.09672)].
# - More advanced noise scheduler than the linear one can give better performance and decrease inference time [[6](https://arxiv.org/abs/2010.02502)]
# - Diffusion in the pixel space is slow. Latent diffusion, in the embedding space, can speed-up inference time greatly [[7](https://openaccess.thecvf.com/content/CVPR2022/html/Rombach_High-Resolution_Image_Synthesis_With_Latent_Diffusion_Models_CVPR_2022_paper.html)]
# ## Conditioned generation with diffusion guidance
# ### Score-Based Generative Models
#
# - Different from DDPM, yet equivalent in nature, are the **score-based** methods [[8](https://openreview.net/forum?id=PxTIG12RRHS)]
# - *Score-based generative models* and DDPM are different perspectives of the same model family
# - In this perspective, the desnoising process corresponds to taking steps in the direction of the **score function**
# $$\nabla_x \log{p(x)}$$
# i.e., the direction where the log-likelihood increases the most
# - In the process, noise is added to avoid getting stuck between the modes of the distribution
# - This is called Stochastic Gradient Langevin Dynamics (SGLD)
# 
# ### Conditional models
#
# - In conditional models, we want to model $p(x|y)$
# - In the score-based perspective, it means following during diffusion the score function: $\nabla_x \log{p(x|y)}$
# - By applying Bayes' rule
# $$ p(x|y) = \frac{p(y|x)p(x)}{p(y)}$$
# that gives us
# $$ \nabla_x \log{p(x|y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)} - \nabla_x \log{p(y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)}$$
# - Notice that $p(y|x)$ is exactly what an image classifier tries to fit
# - If the image classifier is a neural net, it is easy to compute $\nabla_x \log{p(y|x)}$
# - We can give different contributions to the score function and the classfier
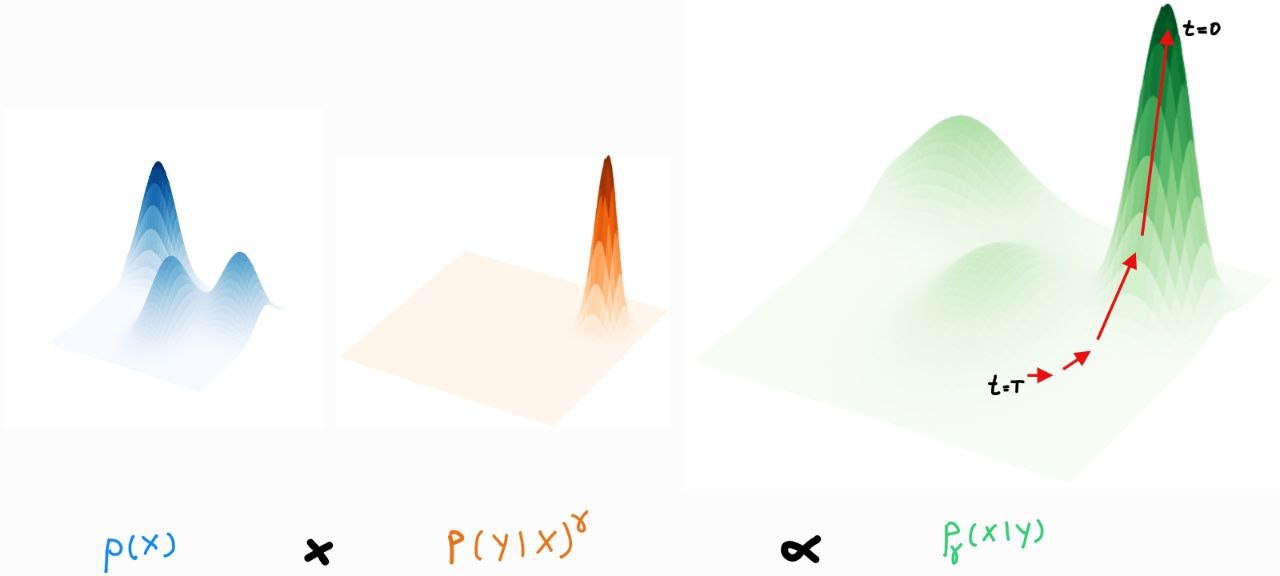
# $$\nabla_x \log{p_\gamma(x|y)} = \nabla_x \log{p(x)} + \gamma \nabla_x \log{p(y|x)},$$ where $\gamma$ is the **guidance scale** [[9](https://proceedings.neurips.cc/paper/2021/file/49ad23d1ec9fa4bd8d77d02681df5cfa-Paper.pdf)]
# - The larger $\gamma$, the larger is the influence of the conditioning signal
# - Reverting the gradient and the logarithm operations, we see that $p_\gamma(x|y) \propto p(x)p(y|x)^\gamma$
# - When $\gamma >1$, this sharpens the distribution and shift probability mass towards the values $x$ that are most likely associated with label $y$
#
#
# In[18]:
from datasets import load_dataset
dataset = load_dataset("fashion_mnist")
image_size = 28
channels = 1
batch_size = 128
# Next, we define some basic image preprocessing on-the-fly: random horizontal flips, converstion to tensor, and rescaling in the $[-1,1]$ range.
#
# We use ``with_transform`` to apply the transformations to the elements in the dataset.
# In[19]:
from torchvision import transforms
from torch.utils.data import DataLoader
# define image transformations (e.g. using torchvision)
transform = Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Lambda(lambda t: (t * 2) - 1)
])
# define function
def transforms(examples):
examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]]
del examples["image"]
return examples
transformed_dataset = dataset.with_transform(transforms).remove_columns("label")
# create dataloader
dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)
# In[20]:
from torch.optim import Adam
device = "cuda" if torch.cuda.is_available() else "cpu"
model = Unet(
dim=image_size,
channels=channels,
dim_mults=(1, 2, 4,)
)
model.to(device)
optimizer = Adam(model.parameters(), lr=1e-3)
# In[21]:
from torchvision.utils import save_image
epochs = 10
for epoch in range(epochs):
for step, batch in enumerate(dataloader):
optimizer.zero_grad()
# x0
batch_size = batch["pixel_values"].shape[0]
batch = batch["pixel_values"].to(device)
# sample t from U(0,T)
t = torch.randint(0, timesteps, (batch_size,), device=device).long()
loss = p_losses(model, batch, t)
if step % 100 == 0:
print(f"Epoch: {epoch}, step: {step} -- Loss: {loss.item():.3f}")
loss.backward()
optimizer.step()
# ### Inference
#
# Once trained, we can sample from the model using ``sample`` the function defined above:
# In[22]:
# Generate 64 images
samples = sample(model, image_size=image_size, batch_size=64, channels=channels)
# Get the last sample and normalize it in [0,1]
last_sample = (samples[-1] - samples[-1].min())/(samples[-1].max()-samples[-1].min())
grid_img = torchvision.utils.make_grid(last_sample, nrow=16)
get_ipython().run_line_magic('matplotlib', 'inline')
plt.figure(figsize = (20,10))
plt.imshow(grid_img.permute(1, 2, 0).cpu().numpy(), cmap='gray');
# Visualize the actual denoising process with an animation
# In[25]:
import matplotlib.animation as animation
get_ipython().run_line_magic('matplotlib', 'notebook')
random_index = 6
fig = plt.figure()
ims = []
for i in range(timesteps):
im = plt.imshow(samples[i][random_index].cpu().numpy().reshape(image_size, image_size, channels), cmap="gray", animated=True)
ims.append([im])
animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)
animate.save('diffusion.gif')
plt.show()
# ## Next steps
#
# - Sample generation can be conditioned on inputs such as text (text2img) and images (img2img) [[4](https://arxiv.org/abs/2204.06125)].
# - Besides the mean, learning the standard deviation $\tilde{\sigma}(\boldsymbol{x}_t)$ of the conditional distribution helps in improving performance [[5](https://arxiv.org/abs/2102.09672)].
# - More advanced noise scheduler than the linear one can give better performance and decrease inference time [[6](https://arxiv.org/abs/2010.02502)]
# - Diffusion in the pixel space is slow. Latent diffusion, in the embedding space, can speed-up inference time greatly [[7](https://openaccess.thecvf.com/content/CVPR2022/html/Rombach_High-Resolution_Image_Synthesis_With_Latent_Diffusion_Models_CVPR_2022_paper.html)]
# ## Conditioned generation with diffusion guidance
# ### Score-Based Generative Models
#
# - Different from DDPM, yet equivalent in nature, are the **score-based** methods [[8](https://openreview.net/forum?id=PxTIG12RRHS)]
# - *Score-based generative models* and DDPM are different perspectives of the same model family
# - In this perspective, the desnoising process corresponds to taking steps in the direction of the **score function**
# $$\nabla_x \log{p(x)}$$
# i.e., the direction where the log-likelihood increases the most
# - In the process, noise is added to avoid getting stuck between the modes of the distribution
# - This is called Stochastic Gradient Langevin Dynamics (SGLD)
# 
# ### Conditional models
#
# - In conditional models, we want to model $p(x|y)$
# - In the score-based perspective, it means following during diffusion the score function: $\nabla_x \log{p(x|y)}$
# - By applying Bayes' rule
# $$ p(x|y) = \frac{p(y|x)p(x)}{p(y)}$$
# that gives us
# $$ \nabla_x \log{p(x|y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)} - \nabla_x \log{p(y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)}$$
# - Notice that $p(y|x)$ is exactly what an image classifier tries to fit
# - If the image classifier is a neural net, it is easy to compute $\nabla_x \log{p(y|x)}$
# - We can give different contributions to the score function and the classfier
# $$\nabla_x \log{p_\gamma(x|y)} = \nabla_x \log{p(x)} + \gamma \nabla_x \log{p(y|x)},$$ where $\gamma$ is the **guidance scale** [[9](https://proceedings.neurips.cc/paper/2021/file/49ad23d1ec9fa4bd8d77d02681df5cfa-Paper.pdf)]
# - The larger $\gamma$, the larger is the influence of the conditioning signal
# - Reverting the gradient and the logarithm operations, we see that $p_\gamma(x|y) \propto p(x)p(y|x)^\gamma$
# - When $\gamma >1$, this sharpens the distribution and shift probability mass towards the values $x$ that are most likely associated with label $y$
#
#  # - ⚠️ Important: the diffusion model is trained as before and *only* at inference time is conditioned by a (pre-trained) classifier
# - Similar to train a powerful unconditional NLP model and adapt it to downstream tasks via few-shot learning
# **Limitations**
#
# ❌ Pre-trained classifiers cannot deal with noise
# - The classifier used for guidance needs to cope with high noise to provide a useful signal through the sampling process
# - This usually requires training the classifier specifically for the purpose of guidance
# - At that point, it might be easier to train a traditional conditional generative model end-to-end...
#
# ❌ Classifiers take shortcuts
# - Most of the information in the input $x$ is not accounted in predicting $y$
# - As result, taking the gradient of the classifier w.r.t. its input can yield arbitrary directions in input space
# ### Classifier-free guidance (cfg)
#
# - We said that $\nabla_x \log{p(x|y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)}$
# - Now, let's express the conditioning term as a function of the conditional and unconditional score functions, both of which our diffusion model provides
# $$ \nabla_x \log{p(y|x)} = \nabla_x \log{p(x|y)} - \nabla_x \log{p(x)}$$
#
# - Then, we substitute this into the formula for classifier guidance:
# $$ \nabla_x \log{p_\gamma(x|y)} = \nabla_x \log{p(x)} + \gamma \big[ \nabla_x \log{p(x|y)} - \nabla_x \log{p(x)} \big]$$
# - We expressed the conditional score function as a combination of the conditional and the unconditional score function itself
# - We no longer need a classifier!
# - cfg is implemented by removing the conditioning signal 10-20\% of times while training (**conditioning dropout**)[[11](https://arxiv.org/abs/2112.10741)]
# - In practice, one replaces $y$ with a special input value representing the absence of conditioning information (e.g., ``""``)
# - The resulting model is now able to function both as a conditional model $p(x|y)$ and as an unconditional model $p(x)$, depending on whether the conditioning signal is provided
#
# Example: "*A stained glass window of a panda eating bamboo.*" with classifier guidance (left) and with cfg (right)
#
# 
# Why cfg is better than classifier guidance?
# - cfg replaces the guidance from a standard classifier $\nabla_x \log{p(y|x)}$ with a "classifier" built from a generative model $\nabla_x \log{p(x|y)} - \nabla_x \log{p(x)}$.
# - Standard classifiers can take shortcuts and ignore most of the input $x$ while still obtaining competitive classification results
# - Instead, generative models are forced to consider the whole data distribution, making the gradient much more robust
# - In addtion, we only have to train a single (generative) model, and conditioning dropout is trivial to implement
#
# Limitation:
# - cfg dramatically improves adherence to the conditioning signal and the overall sample quality at the cost of diversity
# - This is a tipycal trade-off in generative models
# ### References
#
#
# [[1](https://proceedings.neurips.cc/paper/2020/file/4c5bcfec8584af0d967f1ab10179ca4b-Paper.pdf)] Ho, J., Jain, A., Abbeel, P., (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems.
#
# [[2](https://huggingface.co/blog/annotated-diffusion)] Rogge, N., Rasul, K., (2022). The Annotated Diffusion Model.
#
# [[3](https://benanne.github.io/2022/05/26/guidance.html)] Dieleman, S., (2022). Guidance: a cheat code for diffusion models.
#
# [[4](https://arxiv.org/abs/2204.06125)] Ramesh, A., Dhariwal, P., Nichol, A., Chu, C., & Chen, M. (2022). Hierarchical text-conditional image generation with clip latents.
#
# [[5](https://arxiv.org/abs/2102.09672)] Nichol, A. Q., & Dhariwal, P. (2021). Improved denoising diffusion probabilistic models. In International Conference on Machine Learning.
#
# [[6](https://arxiv.org/abs/2010.02502)] Song, J., Meng, C., & Ermon, S. (2020). Denoising diffusion implicit models.
#
# [[7](https://openaccess.thecvf.com/content/CVPR2022/html/Rombach_High-Resolution_Image_Synthesis_With_Latent_Diffusion_Models_CVPR_2022_paper.html)] Rombach, R., Blattmann, A., Lorenz, D., Esser, P., & Ommer, B. (2022). High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition.
#
# [[8](https://openreview.net/forum?id=PxTIG12RRHS)] Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2021). Score-Based Generative Modeling through Stochastic Differential Equations. International Conference on Learning Representations.
#
# [[9](https://proceedings.neurips.cc/paper/2021/file/49ad23d1ec9fa4bd8d77d02681df5cfa-Paper.pdf)] Dhariwal, P., & Nichol, A. (2021). Diffusion models beat gans on image synthesis. Advances in Neural Information Processing Systems.
#
# [[10](https://lilianweng.github.io/posts/2021-07-11-diffusion-models/)] Weng, L., (2021). What are diffusion models?
#
# [[11](https://arxiv.org/abs/2112.10741)] Nichol, A., Dhariwal, P., Ramesh, A., Shyam, P., Mishkin, P., McGrew, B., ... & Chen, M. (2021). Glide: Towards photorealistic image generation and editing with text-guided diffusion models.
#
# - ⚠️ Important: the diffusion model is trained as before and *only* at inference time is conditioned by a (pre-trained) classifier
# - Similar to train a powerful unconditional NLP model and adapt it to downstream tasks via few-shot learning
# **Limitations**
#
# ❌ Pre-trained classifiers cannot deal with noise
# - The classifier used for guidance needs to cope with high noise to provide a useful signal through the sampling process
# - This usually requires training the classifier specifically for the purpose of guidance
# - At that point, it might be easier to train a traditional conditional generative model end-to-end...
#
# ❌ Classifiers take shortcuts
# - Most of the information in the input $x$ is not accounted in predicting $y$
# - As result, taking the gradient of the classifier w.r.t. its input can yield arbitrary directions in input space
# ### Classifier-free guidance (cfg)
#
# - We said that $\nabla_x \log{p(x|y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)}$
# - Now, let's express the conditioning term as a function of the conditional and unconditional score functions, both of which our diffusion model provides
# $$ \nabla_x \log{p(y|x)} = \nabla_x \log{p(x|y)} - \nabla_x \log{p(x)}$$
#
# - Then, we substitute this into the formula for classifier guidance:
# $$ \nabla_x \log{p_\gamma(x|y)} = \nabla_x \log{p(x)} + \gamma \big[ \nabla_x \log{p(x|y)} - \nabla_x \log{p(x)} \big]$$
# - We expressed the conditional score function as a combination of the conditional and the unconditional score function itself
# - We no longer need a classifier!
# - cfg is implemented by removing the conditioning signal 10-20\% of times while training (**conditioning dropout**)[[11](https://arxiv.org/abs/2112.10741)]
# - In practice, one replaces $y$ with a special input value representing the absence of conditioning information (e.g., ``""``)
# - The resulting model is now able to function both as a conditional model $p(x|y)$ and as an unconditional model $p(x)$, depending on whether the conditioning signal is provided
#
# Example: "*A stained glass window of a panda eating bamboo.*" with classifier guidance (left) and with cfg (right)
#
# 
# Why cfg is better than classifier guidance?
# - cfg replaces the guidance from a standard classifier $\nabla_x \log{p(y|x)}$ with a "classifier" built from a generative model $\nabla_x \log{p(x|y)} - \nabla_x \log{p(x)}$.
# - Standard classifiers can take shortcuts and ignore most of the input $x$ while still obtaining competitive classification results
# - Instead, generative models are forced to consider the whole data distribution, making the gradient much more robust
# - In addtion, we only have to train a single (generative) model, and conditioning dropout is trivial to implement
#
# Limitation:
# - cfg dramatically improves adherence to the conditioning signal and the overall sample quality at the cost of diversity
# - This is a tipycal trade-off in generative models
# ### References
#
#
# [[1](https://proceedings.neurips.cc/paper/2020/file/4c5bcfec8584af0d967f1ab10179ca4b-Paper.pdf)] Ho, J., Jain, A., Abbeel, P., (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems.
#
# [[2](https://huggingface.co/blog/annotated-diffusion)] Rogge, N., Rasul, K., (2022). The Annotated Diffusion Model.
#
# [[3](https://benanne.github.io/2022/05/26/guidance.html)] Dieleman, S., (2022). Guidance: a cheat code for diffusion models.
#
# [[4](https://arxiv.org/abs/2204.06125)] Ramesh, A., Dhariwal, P., Nichol, A., Chu, C., & Chen, M. (2022). Hierarchical text-conditional image generation with clip latents.
#
# [[5](https://arxiv.org/abs/2102.09672)] Nichol, A. Q., & Dhariwal, P. (2021). Improved denoising diffusion probabilistic models. In International Conference on Machine Learning.
#
# [[6](https://arxiv.org/abs/2010.02502)] Song, J., Meng, C., & Ermon, S. (2020). Denoising diffusion implicit models.
#
# [[7](https://openaccess.thecvf.com/content/CVPR2022/html/Rombach_High-Resolution_Image_Synthesis_With_Latent_Diffusion_Models_CVPR_2022_paper.html)] Rombach, R., Blattmann, A., Lorenz, D., Esser, P., & Ommer, B. (2022). High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition.
#
# [[8](https://openreview.net/forum?id=PxTIG12RRHS)] Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2021). Score-Based Generative Modeling through Stochastic Differential Equations. International Conference on Learning Representations.
#
# [[9](https://proceedings.neurips.cc/paper/2021/file/49ad23d1ec9fa4bd8d77d02681df5cfa-Paper.pdf)] Dhariwal, P., & Nichol, A. (2021). Diffusion models beat gans on image synthesis. Advances in Neural Information Processing Systems.
#
# [[10](https://lilianweng.github.io/posts/2021-07-11-diffusion-models/)] Weng, L., (2021). What are diffusion models?
#
# [[11](https://arxiv.org/abs/2112.10741)] Nichol, A., Dhariwal, P., Ramesh, A., Shyam, P., Mishkin, P., McGrew, B., ... & Chen, M. (2021). Glide: Towards photorealistic image generation and editing with text-guided diffusion models.
#
 # ### Forward process
#
# ### Forward process
#  # **Nice property:** Let $\alpha_t = 1 - \beta_t$ and $\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$
#
# \begin{align}
# \boldsymbol{x}_t & = \sqrt{\alpha_t} \boldsymbol{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1} \;\;\; \text{where} \;\boldsymbol{z}_{t-1}, \boldsymbol{z}_{t-2}, \dots, \mathcal{N}(\mathbf{0}, \mathbf{I}).\\
# & = \sqrt{\alpha_t} \lbrack \sqrt{\alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{1- \alpha_{t-1}}\boldsymbol{z}_{t-2} \rbrack + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1}\\
# & = \sqrt{\alpha_t \alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}}\boldsymbol{z}_{t-2} + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1}\\
# & = \sqrt{\alpha_t \alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}}\boldsymbol{\bar{z}}_{t-2} \;\;\; \text{where} \; \boldsymbol{\bar{z}}_{t-2} \; \text{merges two Gaussians}^1 \\
# & = \dots \\
# & = \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\bar{z}_0} \;\;\; \text{where} \; \boldsymbol{\bar{z}_0} = \boldsymbol{z} \\
# q(\boldsymbol{x}_t|\boldsymbol{x}_0) & = \mathcal{N}(\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0, 1 - \bar{\alpha}_t)
# \end{align}
#
# $^1$ the sum of two Gaussian variables $\boldsymbol{z}_1 \sim \mathcal{N}(\mathbf{0}, \sigma_1^2 \mathbf{I})$ and $\boldsymbol{z}_2 \sim \mathcal{N}(\mathbf{0}, \sigma_2^2 \mathbf{I})$ is a new variable $\bar{\boldsymbol{z}} \sim \mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2) \mathbf{I})$. In our case, $\boldsymbol{z}_{t-1} \sim \mathcal{N}(\mathbf{0}, (1-\alpha_t) \mathbf{I})$ and $\boldsymbol{z}_{t-2} \sim \mathcal{N}(\mathbf{0}, (\alpha_t - \alpha_t \alpha_{t-1}) \mathbf{I})$, so $\boldsymbol{\bar{z}}_{t-2} \sim \mathcal{N}(\mathbf{0}, (1 - \alpha_t \alpha_{t-1}) \mathbf{I})$.
# In[1]:
import numpy as np
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
import torch
from torch import nn
import torch.nn.functional as F
import torchvision
# First, we define the scheduler to compute $\beta_t$. The simplest is the linear scheduler, but more advanced schedulers can give better results.
# In[2]:
def linear_beta_schedule(timesteps):
beta_start = 0.0001
beta_end = 0.02
return torch.linspace(beta_start, beta_end, timesteps)
# In[3]:
timesteps = 200
# compute betas
betas = linear_beta_schedule(timesteps=timesteps)
# compute alphas
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
# calculations for the forward diffusion q(x_t | x_{t-1})
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)
# Let's illustrate how noise is added to a sample image at each time step of the diffusion process.
# In[4]:
from PIL import Image
image = Image.open("img/lion_short.png")
image
# Next, we resize the image, rescale it in $[-1, 1]$, and convert it to a PyTorch tensor.
# In[5]:
from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize
image_size = 128
transform = Compose([
Resize(image_size),
ToTensor(), # turn into Numpy array of shape HWC, divide by 255
Lambda(lambda t: (t * 2) - 1), # [0,1] --> [-1,1]
])
x_start = transform(image).unsqueeze(0)
x_start.shape
# We also define the reverse transform, which maps a PyTorch tensor with in $[−1,1]$ back into a PIL image.
# In[6]:
reverse_transform = Compose([
Lambda(lambda t: (t + 1) / 2),
Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC
Lambda(lambda t: t * 255.),
Lambda(lambda t: t.numpy().astype(np.uint8)),
ToPILImage(),
])
reverse_transform(x_start.squeeze())
# We can now define the forward diffusion process.
# In[7]:
# utility function to extract the appropriate t index for a batch of indices.
# e.g., t=[10,11], x_shape=[b,c,h,w] --> a.shape = [2,1,1,1]
# e.g., t=[7,12,15,20], x_shape=[b,h,w] --> a.shape = [4,1,1]
def extract(a, t, x_shape):
batch_size = t.shape[0]
out = a.gather(-1, t.cpu())
return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)
# forward diffusion (using the nice property)
def q_sample(x_start, t, noise=None):
if noise is None:
noise = torch.randn_like(x_start) # z (it does not depend on t!)
# adjust the shape
sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x_start.shape
)
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
# Let's test on a specific time step, $t=20$:
# In[8]:
def get_noisy_image(x_start, t):
x_noisy = q_sample(x_start, t=t) # add noise
noisy_image = reverse_transform(x_noisy.squeeze()) # turn back into PIL image
return noisy_image
# In[9]:
t = torch.tensor([19])
get_noisy_image(x_start[0], t)
# In[10]:
def plot_seq(imgs, with_orig=False, row_title=None, **imshow_kwargs):
if not isinstance(imgs[0], list):
# Make a 2d grid even if there's just 1 row
imgs = [imgs]
num_rows = len(imgs)
num_cols = len(imgs[0]) + with_orig
fig, axs = plt.subplots(figsize=(200,200), nrows=num_rows, ncols=num_cols, squeeze=False)
for row_idx, row in enumerate(imgs):
row = [image] + row if with_orig else row
for col_idx, img in enumerate(row):
ax = axs[row_idx, col_idx]
ax.imshow(np.asarray(img), **imshow_kwargs)
ax.set(xticklabels=[], yticklabels=[], xticks=[], yticks=[])
if with_orig:
axs[0, 0].set(title='Original image')
axs[0, 0].title.set_size(8)
if row_title is not None:
for row_idx in range(num_rows):
axs[row_idx, 0].set(ylabel=row_title[row_idx])
plt.tight_layout()
# In[11]:
plot_seq([get_noisy_image(x_start, torch.tensor([t])) for t in [1, 50, 100, 150, 199]])
# ### Backward process
#
# **Nice property:** Let $\alpha_t = 1 - \beta_t$ and $\bar{\alpha}_t = \prod_{i=1}^t \alpha_i$
#
# \begin{align}
# \boldsymbol{x}_t & = \sqrt{\alpha_t} \boldsymbol{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1} \;\;\; \text{where} \;\boldsymbol{z}_{t-1}, \boldsymbol{z}_{t-2}, \dots, \mathcal{N}(\mathbf{0}, \mathbf{I}).\\
# & = \sqrt{\alpha_t} \lbrack \sqrt{\alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{1- \alpha_{t-1}}\boldsymbol{z}_{t-2} \rbrack + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1}\\
# & = \sqrt{\alpha_t \alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}}\boldsymbol{z}_{t-2} + \sqrt{1 - \alpha_t}\boldsymbol{z}_{t-1}\\
# & = \sqrt{\alpha_t \alpha_{t-1}} \boldsymbol{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}}\boldsymbol{\bar{z}}_{t-2} \;\;\; \text{where} \; \boldsymbol{\bar{z}}_{t-2} \; \text{merges two Gaussians}^1 \\
# & = \dots \\
# & = \sqrt{\bar{\alpha}_t} \boldsymbol{x}_0 + \sqrt{1 - \bar{\alpha}_t} \boldsymbol{\bar{z}_0} \;\;\; \text{where} \; \boldsymbol{\bar{z}_0} = \boldsymbol{z} \\
# q(\boldsymbol{x}_t|\boldsymbol{x}_0) & = \mathcal{N}(\sqrt{\bar{\alpha}_t} \boldsymbol{x}_0, 1 - \bar{\alpha}_t)
# \end{align}
#
# $^1$ the sum of two Gaussian variables $\boldsymbol{z}_1 \sim \mathcal{N}(\mathbf{0}, \sigma_1^2 \mathbf{I})$ and $\boldsymbol{z}_2 \sim \mathcal{N}(\mathbf{0}, \sigma_2^2 \mathbf{I})$ is a new variable $\bar{\boldsymbol{z}} \sim \mathcal{N}(\mathbf{0}, (\sigma_1^2 + \sigma_2^2) \mathbf{I})$. In our case, $\boldsymbol{z}_{t-1} \sim \mathcal{N}(\mathbf{0}, (1-\alpha_t) \mathbf{I})$ and $\boldsymbol{z}_{t-2} \sim \mathcal{N}(\mathbf{0}, (\alpha_t - \alpha_t \alpha_{t-1}) \mathbf{I})$, so $\boldsymbol{\bar{z}}_{t-2} \sim \mathcal{N}(\mathbf{0}, (1 - \alpha_t \alpha_{t-1}) \mathbf{I})$.
# In[1]:
import numpy as np
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
import torch
from torch import nn
import torch.nn.functional as F
import torchvision
# First, we define the scheduler to compute $\beta_t$. The simplest is the linear scheduler, but more advanced schedulers can give better results.
# In[2]:
def linear_beta_schedule(timesteps):
beta_start = 0.0001
beta_end = 0.02
return torch.linspace(beta_start, beta_end, timesteps)
# In[3]:
timesteps = 200
# compute betas
betas = linear_beta_schedule(timesteps=timesteps)
# compute alphas
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
# calculations for the forward diffusion q(x_t | x_{t-1})
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)
# Let's illustrate how noise is added to a sample image at each time step of the diffusion process.
# In[4]:
from PIL import Image
image = Image.open("img/lion_short.png")
image
# Next, we resize the image, rescale it in $[-1, 1]$, and convert it to a PyTorch tensor.
# In[5]:
from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize
image_size = 128
transform = Compose([
Resize(image_size),
ToTensor(), # turn into Numpy array of shape HWC, divide by 255
Lambda(lambda t: (t * 2) - 1), # [0,1] --> [-1,1]
])
x_start = transform(image).unsqueeze(0)
x_start.shape
# We also define the reverse transform, which maps a PyTorch tensor with in $[−1,1]$ back into a PIL image.
# In[6]:
reverse_transform = Compose([
Lambda(lambda t: (t + 1) / 2),
Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC
Lambda(lambda t: t * 255.),
Lambda(lambda t: t.numpy().astype(np.uint8)),
ToPILImage(),
])
reverse_transform(x_start.squeeze())
# We can now define the forward diffusion process.
# In[7]:
# utility function to extract the appropriate t index for a batch of indices.
# e.g., t=[10,11], x_shape=[b,c,h,w] --> a.shape = [2,1,1,1]
# e.g., t=[7,12,15,20], x_shape=[b,h,w] --> a.shape = [4,1,1]
def extract(a, t, x_shape):
batch_size = t.shape[0]
out = a.gather(-1, t.cpu())
return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)
# forward diffusion (using the nice property)
def q_sample(x_start, t, noise=None):
if noise is None:
noise = torch.randn_like(x_start) # z (it does not depend on t!)
# adjust the shape
sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x_start.shape
)
return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise
# Let's test on a specific time step, $t=20$:
# In[8]:
def get_noisy_image(x_start, t):
x_noisy = q_sample(x_start, t=t) # add noise
noisy_image = reverse_transform(x_noisy.squeeze()) # turn back into PIL image
return noisy_image
# In[9]:
t = torch.tensor([19])
get_noisy_image(x_start[0], t)
# In[10]:
def plot_seq(imgs, with_orig=False, row_title=None, **imshow_kwargs):
if not isinstance(imgs[0], list):
# Make a 2d grid even if there's just 1 row
imgs = [imgs]
num_rows = len(imgs)
num_cols = len(imgs[0]) + with_orig
fig, axs = plt.subplots(figsize=(200,200), nrows=num_rows, ncols=num_cols, squeeze=False)
for row_idx, row in enumerate(imgs):
row = [image] + row if with_orig else row
for col_idx, img in enumerate(row):
ax = axs[row_idx, col_idx]
ax.imshow(np.asarray(img), **imshow_kwargs)
ax.set(xticklabels=[], yticklabels=[], xticks=[], yticks=[])
if with_orig:
axs[0, 0].set(title='Original image')
axs[0, 0].title.set_size(8)
if row_title is not None:
for row_idx in range(num_rows):
axs[row_idx, 0].set(ylabel=row_title[row_idx])
plt.tight_layout()
# In[11]:
plot_seq([get_noisy_image(x_start, torch.tensor([t])) for t in [1, 50, 100, 150, 199]])
# ### Backward process
#  #
# - If $\beta_t$ is small enough, $q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$ will be a Gaussian $\mathcal{N}\big(\tilde{\mu}(\boldsymbol{x}_t), \tilde{\sigma}(\boldsymbol{x}_t)\big)$
# - However, we cannot compute $\tilde{\mu}(\boldsymbol{x}_t)$ and $\tilde{\sigma}(\boldsymbol{x}_t)$ analytically, because requires knowing the true data distribution $p(\boldsymbol{x})$
# $$ q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)q(\boldsymbol{x}_{t-2}|\boldsymbol{x}_{t-1})\dots \rightarrow p(\boldsymbol{x}_0)$$
# - We can use a NN to learn $\tilde{\mu}(\boldsymbol{x}_t)$ and $\tilde{\sigma}(\boldsymbol{x}_t)$
# ### Simplification
#
# Represent $\tilde{\sigma}(\boldsymbol{x}_t)$ with a time dependent constant $\tilde{\beta}_t$
#
# ### Manipulation
#
# Condition on $\boldsymbol{x}_0$ and obtain
# $q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t$ ,
# $\boldsymbol{x}_0$
# $)$
# $ = \mathcal{N} \big( $
# $\tilde{\mu}(\boldsymbol{x}_t, \boldsymbol{x}_0)$ ,
# $\tilde{\beta}_t$
# $\big) = \mathcal{N} \big( $
# $\tilde{\mu}_t$ ,
# $\tilde{\beta}_t$
# $\big)$
#
# where
#
#
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
#
# and
#
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
#
#
# - If $\beta_t$ is small enough, $q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)$ will be a Gaussian $\mathcal{N}\big(\tilde{\mu}(\boldsymbol{x}_t), \tilde{\sigma}(\boldsymbol{x}_t)\big)$
# - However, we cannot compute $\tilde{\mu}(\boldsymbol{x}_t)$ and $\tilde{\sigma}(\boldsymbol{x}_t)$ analytically, because requires knowing the true data distribution $p(\boldsymbol{x})$
# $$ q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t)q(\boldsymbol{x}_{t-2}|\boldsymbol{x}_{t-1})\dots \rightarrow p(\boldsymbol{x}_0)$$
# - We can use a NN to learn $\tilde{\mu}(\boldsymbol{x}_t)$ and $\tilde{\sigma}(\boldsymbol{x}_t)$
# ### Simplification
#
# Represent $\tilde{\sigma}(\boldsymbol{x}_t)$ with a time dependent constant $\tilde{\beta}_t$
#
# ### Manipulation
#
# Condition on $\boldsymbol{x}_0$ and obtain
# $q(\boldsymbol{x}_{t-1}|\boldsymbol{x}_t$ ,
# $\boldsymbol{x}_0$
# $)$
# $ = \mathcal{N} \big( $
# $\tilde{\mu}(\boldsymbol{x}_t, \boldsymbol{x}_0)$ ,
# $\tilde{\beta}_t$
# $\big) = \mathcal{N} \big( $
# $\tilde{\mu}_t$ ,
# $\tilde{\beta}_t$
# $\big)$
#
# where
#
#
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
#
# and
#
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
#  # ### NN Model
#
# - Take a look at
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
# and
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
# - The only thing we do not know is $\boldsymbol{\tilde z}_t$ .
# - We approximate $\boldsymbol{\tilde z}_t$ with a NN.
#
#
#
# ### NN Model
#
# - Take a look at
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
# and
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
# - The only thing we do not know is $\boldsymbol{\tilde z}_t$ .
# - We approximate $\boldsymbol{\tilde z}_t$ with a NN.
#
#
#  #
# As NN, we use a Unet.
# 
# In[12]:
# Let's look at how the time embeddings look like
from scripts.unet import SinusoidalPositionEmbeddings
time_emb = SinusoidalPositionEmbeddings(100)
t1 = time_emb(torch.tensor([10]))
t2 = time_emb(torch.tensor([12]))
t3 = time_emb(torch.tensor([30]))
fig, ax = plt.subplots(figsize=(5,3))
ax.plot(t1.numpy()[0], label='t=10')
ax.plot(t2.numpy()[0], label='t=12')
ax.plot(t3.numpy()[0], label='t=30')
plt.legend();
# In[13]:
# Let's check the input and output of the U-net
from scripts.unet import Unet
temp_model = Unet(
dim=image_size,
channels=3,
dim_mults=(1, 2, 4,)
)
with torch.no_grad():
out = temp_model(x_start, torch.tensor([40]))
print(f"input shape: {x_start.shape}, output shape: { out.shape}")
# ### Loss
#
#
#
# As NN, we use a Unet.
# 
# In[12]:
# Let's look at how the time embeddings look like
from scripts.unet import SinusoidalPositionEmbeddings
time_emb = SinusoidalPositionEmbeddings(100)
t1 = time_emb(torch.tensor([10]))
t2 = time_emb(torch.tensor([12]))
t3 = time_emb(torch.tensor([30]))
fig, ax = plt.subplots(figsize=(5,3))
ax.plot(t1.numpy()[0], label='t=10')
ax.plot(t2.numpy()[0], label='t=12')
ax.plot(t3.numpy()[0], label='t=30')
plt.legend();
# In[13]:
# Let's check the input and output of the U-net
from scripts.unet import Unet
temp_model = Unet(
dim=image_size,
channels=3,
dim_mults=(1, 2, 4,)
)
with torch.no_grad():
out = temp_model(x_start, torch.tensor([40]))
print(f"input shape: {x_start.shape}, output shape: { out.shape}")
# ### Loss
#
#  #
#
#
# - Loss: $ \| $ $\boldsymbol{ z}_{t-1}$ - $\boldsymbol{\tilde z}_{t}$ $\|_1 = \| $ $\boldsymbol{ z}_{t-1}$ - NN$(\boldsymbol{x}_t, t)$ $\|_1$
# - $\boldsymbol{ z}_{t-1}$ is the noise used to compute $\boldsymbol{x}_t$ in the forward process
# - Remember that to compute $\boldsymbol{x}_t$ we dropped the time index on $\boldsymbol{z}$ (nice property):
# $$ \boldsymbol{x}_t = \sqrt{\bar \alpha_t} \boldsymbol{x}_0 + \sqrt{1 - \bar \alpha_t} \boldsymbol{z} $$
# - Simply, we can sample $\boldsymbol{z}$ , compute $\boldsymbol{x}_t$, and recover $\boldsymbol{z}$ with the $NN$
# ### Training
#
#
#
#
#
# - Loss: $ \| $ $\boldsymbol{ z}_{t-1}$ - $\boldsymbol{\tilde z}_{t}$ $\|_1 = \| $ $\boldsymbol{ z}_{t-1}$ - NN$(\boldsymbol{x}_t, t)$ $\|_1$
# - $\boldsymbol{ z}_{t-1}$ is the noise used to compute $\boldsymbol{x}_t$ in the forward process
# - Remember that to compute $\boldsymbol{x}_t$ we dropped the time index on $\boldsymbol{z}$ (nice property):
# $$ \boldsymbol{x}_t = \sqrt{\bar \alpha_t} \boldsymbol{x}_0 + \sqrt{1 - \bar \alpha_t} \boldsymbol{z} $$
# - Simply, we can sample $\boldsymbol{z}$ , compute $\boldsymbol{x}_t$, and recover $\boldsymbol{z}$ with the $NN$
# ### Training
#
#  #
# **repeat**
# - Sample an image from the training data
# - $\boldsymbol{x}_0 \sim p(\boldsymbol{x}_0)$
# - Sample $\boldsymbol{ z}$ and $t$ randomly
# - $t \sim \mathcal{U}([1, T])$
# - $\boldsymbol{ z}$ $\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$
# - Take gradient descent step on
# $ \nabla_\theta \|$
# $\boldsymbol{ z}$ -
#
# NN$( \sqrt{\bar \alpha_t} \boldsymbol{x}_0 + \sqrt{1 - \bar \alpha_t}$
#
#
# $\boldsymbol{z}$
#
#
# $)$
#
# $\|_1 $
#
# **until** converged
# In[14]:
def p_losses(denoise_model, x_start, t, loss_type="huber"):
# random sample z
noise = torch.randn_like(x_start)
# compute x_t
x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
# recover z from x_t with the NN
predicted_noise = denoise_model(x_noisy, t)
if loss_type == 'l1':
loss = F.l1_loss(noise, predicted_noise)
elif loss_type == 'l2':
loss = F.mse_loss(noise, predicted_noise)
elif loss_type == "huber":
loss = F.smooth_l1_loss(noise, predicted_noise)
else:
raise NotImplementedError()
return loss
# ### Sampling
#
# We said that
# $\boldsymbol{x}_{t-1} \sim \mathcal{N} \big( $
# $\tilde{\mu}_t$ ,
# $\tilde{\beta}_t$
# $\big)$
# where
#
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
# and
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
#
#
#
# **repeat**
# - Sample an image from the training data
# - $\boldsymbol{x}_0 \sim p(\boldsymbol{x}_0)$
# - Sample $\boldsymbol{ z}$ and $t$ randomly
# - $t \sim \mathcal{U}([1, T])$
# - $\boldsymbol{ z}$ $\sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$
# - Take gradient descent step on
# $ \nabla_\theta \|$
# $\boldsymbol{ z}$ -
#
# NN$( \sqrt{\bar \alpha_t} \boldsymbol{x}_0 + \sqrt{1 - \bar \alpha_t}$
#
#
# $\boldsymbol{z}$
#
#
# $)$
#
# $\|_1 $
#
# **until** converged
# In[14]:
def p_losses(denoise_model, x_start, t, loss_type="huber"):
# random sample z
noise = torch.randn_like(x_start)
# compute x_t
x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
# recover z from x_t with the NN
predicted_noise = denoise_model(x_noisy, t)
if loss_type == 'l1':
loss = F.l1_loss(noise, predicted_noise)
elif loss_type == 'l2':
loss = F.mse_loss(noise, predicted_noise)
elif loss_type == "huber":
loss = F.smooth_l1_loss(noise, predicted_noise)
else:
raise NotImplementedError()
return loss
# ### Sampling
#
# We said that
# $\boldsymbol{x}_{t-1} \sim \mathcal{N} \big( $
# $\tilde{\mu}_t$ ,
# $\tilde{\beta}_t$
# $\big)$
# where
#
# $\tilde{\beta}_t = \frac{1 - \bar \alpha_{t-1}}{1 - \bar \alpha_{t}} \beta_t$
#
# and
#
# $\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \Big(\boldsymbol{x}_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}}$
#
#
# $\boldsymbol{\tilde z}_t$
#
#
# $\Big)$
#
#
#  # #### *Sampling algorithm*
# $\boldsymbol{x}_T \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$
#
# **for** $t=T-1, \dots, 0$ **do**
# - $\boldsymbol{z} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ if $t > 1$ else $\boldsymbol{z}=0$
# - $\boldsymbol{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \big( \boldsymbol{x}_{t} - \frac{\beta_t}{\sqrt{1 - \bar{ \alpha}_t}}$ NN$(\boldsymbol{x}_t, t)$ $\big) + \tilde \beta_t \boldsymbol{z}$
#
# **return** $\boldsymbol{x}_{0} = \mu_0$
# In[16]:
# calculations for posterior q(x_{t-1} | x_t, x_0) = q(x_{t-1} | t, x_0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod) # β_t
@torch.no_grad()
def p_sample(model, x, t, t_index):
# adjust shapes
betas_t = extract(betas, t, x.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x.shape
)
sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
# Use the NN to predict the mean
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t)
# Draw the next sample
if t_index == 0:
return model_mean
else:
posterior_variance_t = extract(posterior_variance, t, x.shape) # beta_t
noise = torch.randn_like(x) # z
return model_mean + torch.sqrt(posterior_variance_t) * noise # x_{t-1}
# In[17]:
# Sampling loop
@torch.no_grad()
def p_sample_loop(model, shape):
device = next(model.parameters()).device
# start from pure noise (for each example in the batch)
img = torch.randn(shape, device=device)
imgs = []
for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
img = p_sample(model, img, torch.full((shape[0],), i, device=device, dtype=torch.long), i)
imgs.append(img)
return imgs
@torch.no_grad()
def sample(model, image_size, batch_size=16, channels=3):
return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))
# ### Train the model on Fashion MNIST
#
#
# #### *Sampling algorithm*
# $\boldsymbol{x}_T \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$
#
# **for** $t=T-1, \dots, 0$ **do**
# - $\boldsymbol{z} \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I})$ if $t > 1$ else $\boldsymbol{z}=0$
# - $\boldsymbol{x}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \big( \boldsymbol{x}_{t} - \frac{\beta_t}{\sqrt{1 - \bar{ \alpha}_t}}$ NN$(\boldsymbol{x}_t, t)$ $\big) + \tilde \beta_t \boldsymbol{z}$
#
# **return** $\boldsymbol{x}_{0} = \mu_0$
# In[16]:
# calculations for posterior q(x_{t-1} | x_t, x_0) = q(x_{t-1} | t, x_0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod) # β_t
@torch.no_grad()
def p_sample(model, x, t, t_index):
# adjust shapes
betas_t = extract(betas, t, x.shape)
sqrt_one_minus_alphas_cumprod_t = extract(
sqrt_one_minus_alphas_cumprod, t, x.shape
)
sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
# Use the NN to predict the mean
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t)
# Draw the next sample
if t_index == 0:
return model_mean
else:
posterior_variance_t = extract(posterior_variance, t, x.shape) # beta_t
noise = torch.randn_like(x) # z
return model_mean + torch.sqrt(posterior_variance_t) * noise # x_{t-1}
# In[17]:
# Sampling loop
@torch.no_grad()
def p_sample_loop(model, shape):
device = next(model.parameters()).device
# start from pure noise (for each example in the batch)
img = torch.randn(shape, device=device)
imgs = []
for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
img = p_sample(model, img, torch.full((shape[0],), i, device=device, dtype=torch.long), i)
imgs.append(img)
return imgs
@torch.no_grad()
def sample(model, image_size, batch_size=16, channels=3):
return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))
# ### Train the model on Fashion MNIST
#
#  # In[18]:
from datasets import load_dataset
dataset = load_dataset("fashion_mnist")
image_size = 28
channels = 1
batch_size = 128
# Next, we define some basic image preprocessing on-the-fly: random horizontal flips, converstion to tensor, and rescaling in the $[-1,1]$ range.
#
# We use ``with_transform`` to apply the transformations to the elements in the dataset.
# In[19]:
from torchvision import transforms
from torch.utils.data import DataLoader
# define image transformations (e.g. using torchvision)
transform = Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Lambda(lambda t: (t * 2) - 1)
])
# define function
def transforms(examples):
examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]]
del examples["image"]
return examples
transformed_dataset = dataset.with_transform(transforms).remove_columns("label")
# create dataloader
dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)
# In[20]:
from torch.optim import Adam
device = "cuda" if torch.cuda.is_available() else "cpu"
model = Unet(
dim=image_size,
channels=channels,
dim_mults=(1, 2, 4,)
)
model.to(device)
optimizer = Adam(model.parameters(), lr=1e-3)
# In[21]:
from torchvision.utils import save_image
epochs = 10
for epoch in range(epochs):
for step, batch in enumerate(dataloader):
optimizer.zero_grad()
# x0
batch_size = batch["pixel_values"].shape[0]
batch = batch["pixel_values"].to(device)
# sample t from U(0,T)
t = torch.randint(0, timesteps, (batch_size,), device=device).long()
loss = p_losses(model, batch, t)
if step % 100 == 0:
print(f"Epoch: {epoch}, step: {step} -- Loss: {loss.item():.3f}")
loss.backward()
optimizer.step()
# ### Inference
#
# Once trained, we can sample from the model using ``sample`` the function defined above:
# In[22]:
# Generate 64 images
samples = sample(model, image_size=image_size, batch_size=64, channels=channels)
# Get the last sample and normalize it in [0,1]
last_sample = (samples[-1] - samples[-1].min())/(samples[-1].max()-samples[-1].min())
grid_img = torchvision.utils.make_grid(last_sample, nrow=16)
get_ipython().run_line_magic('matplotlib', 'inline')
plt.figure(figsize = (20,10))
plt.imshow(grid_img.permute(1, 2, 0).cpu().numpy(), cmap='gray');
# Visualize the actual denoising process with an animation
# In[25]:
import matplotlib.animation as animation
get_ipython().run_line_magic('matplotlib', 'notebook')
random_index = 6
fig = plt.figure()
ims = []
for i in range(timesteps):
im = plt.imshow(samples[i][random_index].cpu().numpy().reshape(image_size, image_size, channels), cmap="gray", animated=True)
ims.append([im])
animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)
animate.save('diffusion.gif')
plt.show()
# ## Next steps
#
# - Sample generation can be conditioned on inputs such as text (text2img) and images (img2img) [[4](https://arxiv.org/abs/2204.06125)].
# - Besides the mean, learning the standard deviation $\tilde{\sigma}(\boldsymbol{x}_t)$ of the conditional distribution helps in improving performance [[5](https://arxiv.org/abs/2102.09672)].
# - More advanced noise scheduler than the linear one can give better performance and decrease inference time [[6](https://arxiv.org/abs/2010.02502)]
# - Diffusion in the pixel space is slow. Latent diffusion, in the embedding space, can speed-up inference time greatly [[7](https://openaccess.thecvf.com/content/CVPR2022/html/Rombach_High-Resolution_Image_Synthesis_With_Latent_Diffusion_Models_CVPR_2022_paper.html)]
# ## Conditioned generation with diffusion guidance
# ### Score-Based Generative Models
#
# - Different from DDPM, yet equivalent in nature, are the **score-based** methods [[8](https://openreview.net/forum?id=PxTIG12RRHS)]
# - *Score-based generative models* and DDPM are different perspectives of the same model family
# - In this perspective, the desnoising process corresponds to taking steps in the direction of the **score function**
# $$\nabla_x \log{p(x)}$$
# i.e., the direction where the log-likelihood increases the most
# - In the process, noise is added to avoid getting stuck between the modes of the distribution
# - This is called Stochastic Gradient Langevin Dynamics (SGLD)
# 
# ### Conditional models
#
# - In conditional models, we want to model $p(x|y)$
# - In the score-based perspective, it means following during diffusion the score function: $\nabla_x \log{p(x|y)}$
# - By applying Bayes' rule
# $$ p(x|y) = \frac{p(y|x)p(x)}{p(y)}$$
# that gives us
# $$ \nabla_x \log{p(x|y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)} - \nabla_x \log{p(y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)}$$
# - Notice that $p(y|x)$ is exactly what an image classifier tries to fit
# - If the image classifier is a neural net, it is easy to compute $\nabla_x \log{p(y|x)}$
# - We can give different contributions to the score function and the classfier
# $$\nabla_x \log{p_\gamma(x|y)} = \nabla_x \log{p(x)} + \gamma \nabla_x \log{p(y|x)},$$ where $\gamma$ is the **guidance scale** [[9](https://proceedings.neurips.cc/paper/2021/file/49ad23d1ec9fa4bd8d77d02681df5cfa-Paper.pdf)]
# - The larger $\gamma$, the larger is the influence of the conditioning signal
# - Reverting the gradient and the logarithm operations, we see that $p_\gamma(x|y) \propto p(x)p(y|x)^\gamma$
# - When $\gamma >1$, this sharpens the distribution and shift probability mass towards the values $x$ that are most likely associated with label $y$
#
#
# In[18]:
from datasets import load_dataset
dataset = load_dataset("fashion_mnist")
image_size = 28
channels = 1
batch_size = 128
# Next, we define some basic image preprocessing on-the-fly: random horizontal flips, converstion to tensor, and rescaling in the $[-1,1]$ range.
#
# We use ``with_transform`` to apply the transformations to the elements in the dataset.
# In[19]:
from torchvision import transforms
from torch.utils.data import DataLoader
# define image transformations (e.g. using torchvision)
transform = Compose([
transforms.RandomHorizontalFlip(),
transforms.ToTensor(),
transforms.Lambda(lambda t: (t * 2) - 1)
])
# define function
def transforms(examples):
examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]]
del examples["image"]
return examples
transformed_dataset = dataset.with_transform(transforms).remove_columns("label")
# create dataloader
dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)
# In[20]:
from torch.optim import Adam
device = "cuda" if torch.cuda.is_available() else "cpu"
model = Unet(
dim=image_size,
channels=channels,
dim_mults=(1, 2, 4,)
)
model.to(device)
optimizer = Adam(model.parameters(), lr=1e-3)
# In[21]:
from torchvision.utils import save_image
epochs = 10
for epoch in range(epochs):
for step, batch in enumerate(dataloader):
optimizer.zero_grad()
# x0
batch_size = batch["pixel_values"].shape[0]
batch = batch["pixel_values"].to(device)
# sample t from U(0,T)
t = torch.randint(0, timesteps, (batch_size,), device=device).long()
loss = p_losses(model, batch, t)
if step % 100 == 0:
print(f"Epoch: {epoch}, step: {step} -- Loss: {loss.item():.3f}")
loss.backward()
optimizer.step()
# ### Inference
#
# Once trained, we can sample from the model using ``sample`` the function defined above:
# In[22]:
# Generate 64 images
samples = sample(model, image_size=image_size, batch_size=64, channels=channels)
# Get the last sample and normalize it in [0,1]
last_sample = (samples[-1] - samples[-1].min())/(samples[-1].max()-samples[-1].min())
grid_img = torchvision.utils.make_grid(last_sample, nrow=16)
get_ipython().run_line_magic('matplotlib', 'inline')
plt.figure(figsize = (20,10))
plt.imshow(grid_img.permute(1, 2, 0).cpu().numpy(), cmap='gray');
# Visualize the actual denoising process with an animation
# In[25]:
import matplotlib.animation as animation
get_ipython().run_line_magic('matplotlib', 'notebook')
random_index = 6
fig = plt.figure()
ims = []
for i in range(timesteps):
im = plt.imshow(samples[i][random_index].cpu().numpy().reshape(image_size, image_size, channels), cmap="gray", animated=True)
ims.append([im])
animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)
animate.save('diffusion.gif')
plt.show()
# ## Next steps
#
# - Sample generation can be conditioned on inputs such as text (text2img) and images (img2img) [[4](https://arxiv.org/abs/2204.06125)].
# - Besides the mean, learning the standard deviation $\tilde{\sigma}(\boldsymbol{x}_t)$ of the conditional distribution helps in improving performance [[5](https://arxiv.org/abs/2102.09672)].
# - More advanced noise scheduler than the linear one can give better performance and decrease inference time [[6](https://arxiv.org/abs/2010.02502)]
# - Diffusion in the pixel space is slow. Latent diffusion, in the embedding space, can speed-up inference time greatly [[7](https://openaccess.thecvf.com/content/CVPR2022/html/Rombach_High-Resolution_Image_Synthesis_With_Latent_Diffusion_Models_CVPR_2022_paper.html)]
# ## Conditioned generation with diffusion guidance
# ### Score-Based Generative Models
#
# - Different from DDPM, yet equivalent in nature, are the **score-based** methods [[8](https://openreview.net/forum?id=PxTIG12RRHS)]
# - *Score-based generative models* and DDPM are different perspectives of the same model family
# - In this perspective, the desnoising process corresponds to taking steps in the direction of the **score function**
# $$\nabla_x \log{p(x)}$$
# i.e., the direction where the log-likelihood increases the most
# - In the process, noise is added to avoid getting stuck between the modes of the distribution
# - This is called Stochastic Gradient Langevin Dynamics (SGLD)
# 
# ### Conditional models
#
# - In conditional models, we want to model $p(x|y)$
# - In the score-based perspective, it means following during diffusion the score function: $\nabla_x \log{p(x|y)}$
# - By applying Bayes' rule
# $$ p(x|y) = \frac{p(y|x)p(x)}{p(y)}$$
# that gives us
# $$ \nabla_x \log{p(x|y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)} - \nabla_x \log{p(y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)}$$
# - Notice that $p(y|x)$ is exactly what an image classifier tries to fit
# - If the image classifier is a neural net, it is easy to compute $\nabla_x \log{p(y|x)}$
# - We can give different contributions to the score function and the classfier
# $$\nabla_x \log{p_\gamma(x|y)} = \nabla_x \log{p(x)} + \gamma \nabla_x \log{p(y|x)},$$ where $\gamma$ is the **guidance scale** [[9](https://proceedings.neurips.cc/paper/2021/file/49ad23d1ec9fa4bd8d77d02681df5cfa-Paper.pdf)]
# - The larger $\gamma$, the larger is the influence of the conditioning signal
# - Reverting the gradient and the logarithm operations, we see that $p_\gamma(x|y) \propto p(x)p(y|x)^\gamma$
# - When $\gamma >1$, this sharpens the distribution and shift probability mass towards the values $x$ that are most likely associated with label $y$
#
#  # - ⚠️ Important: the diffusion model is trained as before and *only* at inference time is conditioned by a (pre-trained) classifier
# - Similar to train a powerful unconditional NLP model and adapt it to downstream tasks via few-shot learning
# **Limitations**
#
# ❌ Pre-trained classifiers cannot deal with noise
# - The classifier used for guidance needs to cope with high noise to provide a useful signal through the sampling process
# - This usually requires training the classifier specifically for the purpose of guidance
# - At that point, it might be easier to train a traditional conditional generative model end-to-end...
#
# ❌ Classifiers take shortcuts
# - Most of the information in the input $x$ is not accounted in predicting $y$
# - As result, taking the gradient of the classifier w.r.t. its input can yield arbitrary directions in input space
# ### Classifier-free guidance (cfg)
#
# - We said that $\nabla_x \log{p(x|y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)}$
# - Now, let's express the conditioning term as a function of the conditional and unconditional score functions, both of which our diffusion model provides
# $$ \nabla_x \log{p(y|x)} = \nabla_x \log{p(x|y)} - \nabla_x \log{p(x)}$$
#
# - Then, we substitute this into the formula for classifier guidance:
# $$ \nabla_x \log{p_\gamma(x|y)} = \nabla_x \log{p(x)} + \gamma \big[ \nabla_x \log{p(x|y)} - \nabla_x \log{p(x)} \big]$$
# - We expressed the conditional score function as a combination of the conditional and the unconditional score function itself
# - We no longer need a classifier!
# - cfg is implemented by removing the conditioning signal 10-20\% of times while training (**conditioning dropout**)[[11](https://arxiv.org/abs/2112.10741)]
# - In practice, one replaces $y$ with a special input value representing the absence of conditioning information (e.g., ``""``)
# - The resulting model is now able to function both as a conditional model $p(x|y)$ and as an unconditional model $p(x)$, depending on whether the conditioning signal is provided
#
# Example: "*A stained glass window of a panda eating bamboo.*" with classifier guidance (left) and with cfg (right)
#
# 
# Why cfg is better than classifier guidance?
# - cfg replaces the guidance from a standard classifier $\nabla_x \log{p(y|x)}$ with a "classifier" built from a generative model $\nabla_x \log{p(x|y)} - \nabla_x \log{p(x)}$.
# - Standard classifiers can take shortcuts and ignore most of the input $x$ while still obtaining competitive classification results
# - Instead, generative models are forced to consider the whole data distribution, making the gradient much more robust
# - In addtion, we only have to train a single (generative) model, and conditioning dropout is trivial to implement
#
# Limitation:
# - cfg dramatically improves adherence to the conditioning signal and the overall sample quality at the cost of diversity
# - This is a tipycal trade-off in generative models
# ### References
#
#
# [[1](https://proceedings.neurips.cc/paper/2020/file/4c5bcfec8584af0d967f1ab10179ca4b-Paper.pdf)] Ho, J., Jain, A., Abbeel, P., (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems.
#
# [[2](https://huggingface.co/blog/annotated-diffusion)] Rogge, N., Rasul, K., (2022). The Annotated Diffusion Model.
#
# [[3](https://benanne.github.io/2022/05/26/guidance.html)] Dieleman, S., (2022). Guidance: a cheat code for diffusion models.
#
# [[4](https://arxiv.org/abs/2204.06125)] Ramesh, A., Dhariwal, P., Nichol, A., Chu, C., & Chen, M. (2022). Hierarchical text-conditional image generation with clip latents.
#
# [[5](https://arxiv.org/abs/2102.09672)] Nichol, A. Q., & Dhariwal, P. (2021). Improved denoising diffusion probabilistic models. In International Conference on Machine Learning.
#
# [[6](https://arxiv.org/abs/2010.02502)] Song, J., Meng, C., & Ermon, S. (2020). Denoising diffusion implicit models.
#
# [[7](https://openaccess.thecvf.com/content/CVPR2022/html/Rombach_High-Resolution_Image_Synthesis_With_Latent_Diffusion_Models_CVPR_2022_paper.html)] Rombach, R., Blattmann, A., Lorenz, D., Esser, P., & Ommer, B. (2022). High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition.
#
# [[8](https://openreview.net/forum?id=PxTIG12RRHS)] Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2021). Score-Based Generative Modeling through Stochastic Differential Equations. International Conference on Learning Representations.
#
# [[9](https://proceedings.neurips.cc/paper/2021/file/49ad23d1ec9fa4bd8d77d02681df5cfa-Paper.pdf)] Dhariwal, P., & Nichol, A. (2021). Diffusion models beat gans on image synthesis. Advances in Neural Information Processing Systems.
#
# [[10](https://lilianweng.github.io/posts/2021-07-11-diffusion-models/)] Weng, L., (2021). What are diffusion models?
#
# [[11](https://arxiv.org/abs/2112.10741)] Nichol, A., Dhariwal, P., Ramesh, A., Shyam, P., Mishkin, P., McGrew, B., ... & Chen, M. (2021). Glide: Towards photorealistic image generation and editing with text-guided diffusion models.
#
# - ⚠️ Important: the diffusion model is trained as before and *only* at inference time is conditioned by a (pre-trained) classifier
# - Similar to train a powerful unconditional NLP model and adapt it to downstream tasks via few-shot learning
# **Limitations**
#
# ❌ Pre-trained classifiers cannot deal with noise
# - The classifier used for guidance needs to cope with high noise to provide a useful signal through the sampling process
# - This usually requires training the classifier specifically for the purpose of guidance
# - At that point, it might be easier to train a traditional conditional generative model end-to-end...
#
# ❌ Classifiers take shortcuts
# - Most of the information in the input $x$ is not accounted in predicting $y$
# - As result, taking the gradient of the classifier w.r.t. its input can yield arbitrary directions in input space
# ### Classifier-free guidance (cfg)
#
# - We said that $\nabla_x \log{p(x|y)} = \nabla_x \log{p(y|x)} + \nabla_x \log{p(x)}$
# - Now, let's express the conditioning term as a function of the conditional and unconditional score functions, both of which our diffusion model provides
# $$ \nabla_x \log{p(y|x)} = \nabla_x \log{p(x|y)} - \nabla_x \log{p(x)}$$
#
# - Then, we substitute this into the formula for classifier guidance:
# $$ \nabla_x \log{p_\gamma(x|y)} = \nabla_x \log{p(x)} + \gamma \big[ \nabla_x \log{p(x|y)} - \nabla_x \log{p(x)} \big]$$
# - We expressed the conditional score function as a combination of the conditional and the unconditional score function itself
# - We no longer need a classifier!
# - cfg is implemented by removing the conditioning signal 10-20\% of times while training (**conditioning dropout**)[[11](https://arxiv.org/abs/2112.10741)]
# - In practice, one replaces $y$ with a special input value representing the absence of conditioning information (e.g., ``""``)
# - The resulting model is now able to function both as a conditional model $p(x|y)$ and as an unconditional model $p(x)$, depending on whether the conditioning signal is provided
#
# Example: "*A stained glass window of a panda eating bamboo.*" with classifier guidance (left) and with cfg (right)
#
# 
# Why cfg is better than classifier guidance?
# - cfg replaces the guidance from a standard classifier $\nabla_x \log{p(y|x)}$ with a "classifier" built from a generative model $\nabla_x \log{p(x|y)} - \nabla_x \log{p(x)}$.
# - Standard classifiers can take shortcuts and ignore most of the input $x$ while still obtaining competitive classification results
# - Instead, generative models are forced to consider the whole data distribution, making the gradient much more robust
# - In addtion, we only have to train a single (generative) model, and conditioning dropout is trivial to implement
#
# Limitation:
# - cfg dramatically improves adherence to the conditioning signal and the overall sample quality at the cost of diversity
# - This is a tipycal trade-off in generative models
# ### References
#
#
# [[1](https://proceedings.neurips.cc/paper/2020/file/4c5bcfec8584af0d967f1ab10179ca4b-Paper.pdf)] Ho, J., Jain, A., Abbeel, P., (2020). Denoising diffusion probabilistic models. Advances in Neural Information Processing Systems.
#
# [[2](https://huggingface.co/blog/annotated-diffusion)] Rogge, N., Rasul, K., (2022). The Annotated Diffusion Model.
#
# [[3](https://benanne.github.io/2022/05/26/guidance.html)] Dieleman, S., (2022). Guidance: a cheat code for diffusion models.
#
# [[4](https://arxiv.org/abs/2204.06125)] Ramesh, A., Dhariwal, P., Nichol, A., Chu, C., & Chen, M. (2022). Hierarchical text-conditional image generation with clip latents.
#
# [[5](https://arxiv.org/abs/2102.09672)] Nichol, A. Q., & Dhariwal, P. (2021). Improved denoising diffusion probabilistic models. In International Conference on Machine Learning.
#
# [[6](https://arxiv.org/abs/2010.02502)] Song, J., Meng, C., & Ermon, S. (2020). Denoising diffusion implicit models.
#
# [[7](https://openaccess.thecvf.com/content/CVPR2022/html/Rombach_High-Resolution_Image_Synthesis_With_Latent_Diffusion_Models_CVPR_2022_paper.html)] Rombach, R., Blattmann, A., Lorenz, D., Esser, P., & Ommer, B. (2022). High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition.
#
# [[8](https://openreview.net/forum?id=PxTIG12RRHS)] Song, Y., Sohl-Dickstein, J., Kingma, D. P., Kumar, A., Ermon, S., & Poole, B. (2021). Score-Based Generative Modeling through Stochastic Differential Equations. International Conference on Learning Representations.
#
# [[9](https://proceedings.neurips.cc/paper/2021/file/49ad23d1ec9fa4bd8d77d02681df5cfa-Paper.pdf)] Dhariwal, P., & Nichol, A. (2021). Diffusion models beat gans on image synthesis. Advances in Neural Information Processing Systems.
#
# [[10](https://lilianweng.github.io/posts/2021-07-11-diffusion-models/)] Weng, L., (2021). What are diffusion models?
#
# [[11](https://arxiv.org/abs/2112.10741)] Nichol, A., Dhariwal, P., Ramesh, A., Shyam, P., Mishkin, P., McGrew, B., ... & Chen, M. (2021). Glide: Towards photorealistic image generation and editing with text-guided diffusion models.
#