#!/usr/bin/env python
# coding: utf-8

# # Recursión
# 
# ## Definición
# 
# La recursividad se puede definir como la capacidad de una función para construir su respuesta usándose a si misma. La RAE define ``recursivo`` de la siguiente manera:
# 
# <center>Dicho especialmente de un proceso: Que se aplica de nuevo al resultado de haberlo aplicado previamente</center>
# 
# La recursión es una técnica de programación y matemática, se usa para problemas con la siguiente estructura: [Teoria](http://nbviewer.jupyter.org/github/ProgramacionCompetitivaUNI/ProgramacionCompetitivaUNI/blob/master/no-fiis/clase-09/clase-09.ipynb)
# 
# ![](pictures/Recursion.jpg)
# 
# ## Recursión Matemática
# 
# Toda recursión matemática debe estar compuesta por 2 elementos principales:
# 
# - Conjunto de parámetros: Elementos con los cuales se trabaja para hallar la respuesta
# - Definición de la recursión: Proceso que se sigue para hallar la respuesta
# 
# Inclusive, la **definición** de la recursión tiene 2 subelementos:
# 
# - Casos base: Casos que ya no necesitan de la función para dar su respuesta
# - Predicado y recursión: Explicación de la función a resolver y la manera en cómo se logra hacerlo.
# 
# Por ahora todo parece relativamente confuso, pero veamos el caso más simple de recursión: **El factorial**.
# 
# La función factorial (que se expresa como "$x!$ se lee como factorial de x") está definida de la siguiente forma para los números enteros no negativos:
# 
# $$ n! = \left\{   \begin{array}{cc}            1 &n=0 \\            n\cdot (n-1)! &\text{en otro caso} \\        \end{array}    \right. $$
# 
# En este caso, ``f(x) = x!`` (donde $x$ es el conjunto de parámetros), siendo $f(0) = 1$ como caso base y $f(n) = n\cdot f(n-1)$ nuestra recursión para $n \geq 1$. Además, a pesar de ser obvio, el predicado de $f$ es "$f(x)$ da como respuesta el producto de los numeros naturales entre el 1 y $x$".
# 
# 
# ### Las Torres de Hanoi
# 
# Para introducir una manera un poco más formal de analizar las recursiones, veremos el conocido problema de las torres de hanoi, el cual señala lo siguiente:
# 
# - Tenemos 3 postes fijos.
# 
# - En uno de los postes hay 64 discos colocados con un tamaño descreciente desde la base hasta el tope.
# 
# - En un movimiento, podemos llevar un disco del tope de alguno de los postes a otro poste que esté vacio o que el tamaño del primer disco de este sea mayor que el que moveremos.
# 
# - El problema pide mover la torre de discos inicial y colocarlos de esa manera en otro poste.
# 
# La idea es resolver este problema en la menor cantidad de tiempo posible, por lo que debemos determinar la mínima cantidad de movimientos posibles.
# 
# Para resolver recursiones, siempre es bueno ver los casos pequeños para buscar un patrón. En este caso, vamos a generalizar: En vez de 64 discos, supongamos que hay $n$ discos.
# 
# Entoncs, definimos la función $T(n)$ que nos dará la cantidad mínima de movimientos que se deben usar para resolver el problema con $n$ discos.
# 
# Claramente, los casos más pequeños y lógicos serían:
# 
# - $T(0) = 0$, no hay necesidad de movimientos si no hay discos
# 
# - $T(1) = 1$, basta con colocar directamente el disco en el poste deseado
# 
# - $T(2) = 3$, disco 1 -> poste 2, disco 2 -> poste 3, disco 1 -> poste 3
# 
# Ahora, esta función poco a poco toma cierta forma, pero veamos matemáticamente los límites de la función $T$:
# 
# Para mover $n$ discos a otro poste, por la naturaleza del problema, debemos mover la torre de $n-1$ discos superiores antes del $n$-ésimo disco a otro poste, luego movemos este disco al poste deseado y finalmente movemos los otros $n-1$ discos a la torre deseada. Esto se puede denotar como:
# 
# <center>$ T(n) \leq T(n-1) + 1 + T(n-1) $</center>
# 
# <center>$ T(n) \leq 2T(n-1) + 1 $</center>
# 
# Ahora probamos el límite superior; pero si nos damos cuenta, la única situación en la que no se hacen movimientos innecesarios es la explicada anteriormente, pues necesitamos:
# 
# 1) Al menos un poste esté libre
# 
# 2) Salida sin problemas para el $n$-ésimo disco
# 
# Por lo que esto se logra solamente si todos los otros $n-1$ discos están en un poste diferente al original, y por las condiciones, deben estar en forma de torre decreciente de la base al tope, entonces llegamos a que:
# 
# $$ T(n) \geq T(n-1) + 1 + T(n-1) $$
# 
# $$ T(n) \geq 2T(n-1) + 1 $$
# 
# Juntando ambas desigualdades y el caso base $T(0)=0$, llegamos a que:
# 
# $$ T(0) = 0 $$
# 
# 
# 
# $$ T(n) = 2T(n-1)+1, n\geq 1 $$
# 
# Esta recursión se ve similar a la función $f(n) = 2^{n}-1$, pero no estamos completamente seguros a menos que demostremos su veracidad. Probemos por inducción:
# 
# 1) $T(0) = f(0) = 2^{0}-1 = 0$
# 
# 2) $T(n) = f(n) = 2^{n}-1$
# 
# 3) $T(n+1) = 2T(n) + 1 = 2(2^{n}-1)+1 = 2^{n+1}-2+1 = 2^{n+1}-1$ -> Probamos la igualdad de ambas funciones.
# 
# Sin embargo, la meta de las recursiones no es adivinar la relación, sino ser más precisos y obtener conclusiones sin tener que jugar con nuestra suerte. Para evitar ello, plantearemos una manera más sencilla de analizar las recursiones separando por casos más adelante.
# 
# ### Problema de Josephus
# 
# Este problema señala que se colocarán $n$ personas en un círculo, de manera horaria, y en una ronda se eliminan cada 2 personas de las que están presentes. Se repiten las rondas hasta que solo quede una persona. Debemos determinar el número de la persona que queda.
# 
# Una idea intuitiva, para empezar, es que la respuesta nunca será un número par, pues todos ellos son eliminados en la primera ronda.
# 
# Definamos la función $J(n)$ como la que nos dará la respuesta para $n$ personas.
# 
# Ahora, veamos los casos más pequeños:
# 
# | n    | 1 | 2 | 3 | 4 | 5 | 6 |
# |------|---|---|---|---|---|---|
# | J(n) | 1 | 1 | 3 | 1 | 3 | 5 |
# 
# Ciertamente, no parece que haya un patrón estricto, tal vez es una repetición de 1 -> 1,3 -> 1,3,5 -> 1,3,5,7 -> ..., pero esto no nos ayuda a darle forma matemática al problema.
# 
# Veamos el caso para $n=2k$:
# 
# - Hay $2k$ personas inicialmente.
# 
# - En la siguiente ronda han sido eliminadas todas las personas $2i$ y quedan las que tienen numeros $2i+1$.
# 
# - Observación 1: La cantidad de personas ha sido reducida a $k$.
# 
# - Observación 2: Ahora hay $k$ personas, pero sus números son 1,3,5,7,...,2i-1, por lo que la posición de la persona que se salva es igual a $J(k)$ pero su número para $J(2k)$ será $2J(k)-1$ por la biyección que se puede plantear.
# 
# Con lo anterior, llegamos a que:
# 
# $$ J(2k) = 2J(k)-1, k\geq 1 $$
# 
# Ahora, supongamos $n=2k+1$:
# 
# - Hay $2k+1$ personas inicialmente.
# 
# - En la siguiente ronda han sido eliminadas todas las personas $2i$, pero con un paso más se elimina también la persona con número $1$ luego de la persona $2k$.
# 
# - Observación 1: La cantidad de personas ha sido reducida a $k$.
# 
# - Observación 2: Ahora hay $k$ personas, pero sus números son 3,5,7,...,2i+1, por lo que la posición de la persona que se salva es igual a $J(k)$, pero su número para $J(2k+1)$ será $2J(k)+1$.
# 
# Con lo anterior, llegamos a que:
# 
# $$ J(2k+1) = 2J(k)+1, k\geq 1 $$
# 
# Entonces, con el caso base $J(1) = 1$ tenemos:
# 
# $$ J(n) = \left\{ \begin{array}{cc} 1 &n=1 \\ 2J(k)-1 &n=2k, k > 0 \\ 2J(k)+1 &n=2k+1, k > 0 \end{array} \right. $$
# 
# 
# Aun no parece muy clara la recursión, veamos (ahora que nos es más sencillo) varios de los casos pequeños:
# 
# | n    | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
# |------|---|---|---|---|---|---|---|---|---|----|----|----|----|----|----|
# | J(n) | 1 | 1 | 3 | 1 | 3 | 5 | 7 | 1 | 3 | 5  | 7  | 9  | 11 | 13 | 15 |
# 
# Se ve claramente que se va tomando los primeros $2^{i}$ numeros impares y se repite el proceso aumentando $i$ en 1.
# 
# Ahora, notemos que siempre la respuesta es 1 cuando $n = 2^{k}$, y por lo que nos hemos dado cuenta sobre las respuestas, el último número que no tendrá respuesta igual a 1 y que sea mayor que $n$ es precisamente $m=2^{k+1}-1$, pues para llegar al siguiente 1 aumentaríamos $2^{k}$, y basta con restar 1 para obtener el anterior. Entonces, se da la secuencia de los $2^{k}$ primeros números impares desde $n=2^{k}$ hasta $m=2^{k+1}-1$.
# 
# Ahora, si nos damos cuenta, la secuencia de respuestas y sus parámetros están ordenadas, y además lo único que tienen diferente todos los números desde el $n$ hasta el $m$ son los bits hasta el de orden $k-1$. Ahora se nos puede ocurrir pensar en algo como que:
# 
# Si $n = 2^{m} + l$, entonces su respuesta es la posición $l$ (con indexación desde 0) de los primeros impares, la cual sería $2l+1$, con $0 \leq l < 2^{m}$.
# 
# Esto parece tener sentido debido al patrón y a nuestras observaciones, pero demostremos inductivamente que de verdad es la solución:
# 
# - $J(1) = f(2^{0}+0) = 2(0)+1 = 1$.
# 
# - $J(2^{m}+l) = 2l+1$.
# 
# - Supongamos para $n=2^{m}+2k$ par:
# 
#     1) $J(n) = 2J(\frac{n}{2})-1 = 2(2^{m-1}+k)-1 = 2(2k+1)-1 = 4k+1 = 2(2k)+1$, cumple cuando $l$ es par.
# 
# - Supongamos para $n=2^{m}+2k+1$ impar:
#     
#     1) $J(n) = 2J(\frac{n}{2})+1 = 2(2^{m-1}+k)+1 = 2(2k+1)+1 = 4k+3 = 2(2k+1)+1$, cumple cuando $l$ es impar.
# 
# 
# ### Problemas propuestos
# 
# 1) ¿Cuál es la máxima cantidad de regiones que se pueden formar colocando $n$ rectas en un plano?
# 
# 2) Igual que el problema 1, pero esta vez no son rectas, sino lineas infinitas en forma de zig-zag (Como una V rotada e infinita en extensión) 
# 
# 3) Halle la solución para las Torres de Hanoi pero si se da que los movimientos directamente del poste $A$ (original) al $C$ (deseado) no son válidos.
# 
# ## Fractales
# 
# Los fractales son estructuras matemáticas cuya construcción se define por una profundidad como parámetro y un proceso recursivo.
# 
# Son un área de estudio relativamente reciente en las matemáticas, y por su comportamiento, inspira la curiosidad de muchas personas. Este caso no es diferente para programación competitiva, pues existen una cantidad considerable de problemas relacionados con estos.
# 
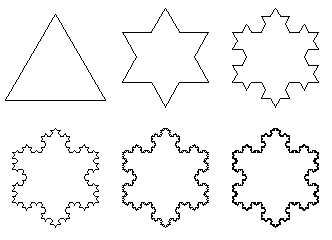
# ### Copo de nieve de Koch
# 
# 1) Se toma un segmento
# 
# 2) Dividir cada segmento en 3 partes iguales, reemplazar la parte central por dos partes iguales formando un ángulo de 60 grados. Repetir hasta llegar a la profundidad deseada
# 
# ![](pictures/Koch.gif)
# 
# Los problemas principalmente tratarán de construir un fractal dado su procedimiento o de intentar analizar cada uno de sus pasos.
# 
# Veamos estos 4 problemas de recursión.
# 
# - [Fit Squares in Triangle - Easy](https://www.codechef.com/problems/TRISQ)
# 
# - [Fractal - Easy](http://www.spoj.com/problems/URJC2_F/)
# 
# - [All Squares - Easy/Medium](https://uva.onlinejudge.org/index.php?option=onlinejudge&page=show_problem&problem=91)
# 
# - [Connecting Soldiers - Medium](https://www.codechef.com/problems/NOKIA)
# 
# ## Fast Exponentiation
# 
# Esta es una manera de optimizar una exponenciación, la cual naturalmente se haría en $O(b)$ siendo $a$ la base y $b$ el exponente, para lograrla en $O(\log{b})$. La idea principalmente es barrer los bits de $b$:
# 
# Supongamos que la representación binaria de $b$ es la siguiente:
# 
# $$ b = b_{k}b_{k-1}\ldots b_{2}b_{1}b_{0} $$
# 
# Entonces podemos representar:
# 
# $$ a^{b} = a^{b_{k}\cdot2^{k} + b_{k-1}\cdot2^{k-1} + \ldots + 2\cdot b_{1} + b_{0}} $$
# 
# Por lo cual podemos plantear lo siguiente:
# 
# $$ a^{b} = a^{b_{0}}\cdot \left(a^{2}\right)^{b_{k}b_{k-1}\ldots b_{2}b_{1}} $$
# 
# Entonces definimos la función $fast\_exp(a,b)$ como la que nos dará el resultado de $a^{b}$:
# 
# $$ fast\_exp(a,b) = a^{b} $$
# 
# Pero por lo que planteamos hace un momento, debemos ver el siguiente patrón:
# 
# $$ fast\_exp(a,b) = a^{b mod 2} \cdot fast\_exp(a^{2},b/2) $$
# 
# Donde $b/2$ es el cociente entero de la división de $b$ entre 2.
# 
# De esta recursión, recordando además que $fast\_exp(a,0) = 1$, podemos plantear el siguiente código:
# 
# ```Cpp
# long long fast_exp(long long a, int b){
#     if(b == 0) return 1LL; // Caso base
#     if(b % 2 == 0) return fast_exp(a*a,b/2); // Si el bit de orden 0 está apagado
#     return a*fast_exp(a*a,b/2); // Si el bit de orden 0 esta prendido
# }
# ```
# 
# Algo beneficioso de esta función es que se puede aplicar a cualquier operación que sea asociativa en repetición, como la suma, coseno de la suma de dos angulos, etc.
# 
# ## Maximo Comun Divisor
# 
# La idea instintiva para hallar el MCD de dos numeros $a$ y $b$ es iterar desde 1 hasta el minimo entre ambos y actualizar cada vez que encontramos un numero que divida a ambos, pero esto tiene una complejidad de $O(min(a,b))$, lo cual no es muy eficiente si usamos números hasta $10^{18}$. Para solucionar este problema, usaremos el algoritmo de Euclides, el cual usa la siguiente recusión (considerando $a \geq b$):
# 
# $$ gcd(a,0) = a $$
# $$ gcd(a,b) = gcd(b,a mod b) $$
# 
# Ahora, la veracidad del funcionamiento del algoritmo está demostrada, pero ¿Qué hay de su complejidad?.
# 
# Para hallar un estimado de su complejidad debemos hallar lo que sucede en cada paso:
# 
# $$ gcd(a,b) \rightarrow (a,b) $$
# $$ gcd(b,a mod b) \rightarrow (b,q),\text{ si } a = bk+q $$
# 
# Y así se da de manera consecutiva. Sin embargo, notemos que el peor de los casos se debería dar cuando $a$ se reduce en lo mínimo posible; y al ser $a \geq b$, se da cuando $a = b+q$. De manera similar, $b = q+r$ y así consecutivamente. Si lo colocamos de una manera más fácil de ver, sería:
# 
# Si fijamos la solución final:
# 
# $$ 0 \rightarrow m \rightarrow n=m \rightarrow s=m+n \rightarrow \cdots \rightarrow b=q+r \rightarrow a=b+q $$
# 
# Notamos que si colocamos la recursión de esta manera (tal que cada paso es tomar dos numeros consecutivos y colocarlos adecuadamente en los parámetros), se parece muchísimo a la sucessión de **Fibonacci**.
# 
# Ciertamente, el peor de los casos se dará cuando $a$ y $b$ son números de Fibonacci consecutivos, en cuyo caso, si $a = F_{n}$ y $b = F_{n-1}$, la siguiente llamada a la función dará $a=F_{n-1}$ y $b=F_{n-2}$ como parámetros, realizando unas $n-1$ iteraciones con la función.
# 
# Con lo anterior, tenemos que $gcd(F_{n},F_{n-1}) = \Theta(n)$ y para cualquier número $a$, $gcd(a,F_{n-1}) = O(n)$. Dado que $F_{n-1} = \Theta(\varphi^{n})$, esto implica aproximadamente que $gcd(a,b) = O(\log_{\varphi}{b})$ pero al ser $\varphi > 2$, entonces también se da que $gcd(a,b) = O(\log_{2}{b})$