#!/usr/bin/env python
# coding: utf-8
# ***
# ***
#
#
# # Introduction to Gradient Descent
#
# The Idea Behind Gradient Descent 梯度下降
#
# ***
# ***
#
#
#  #
#  #
#
# **如何找到最快下山的路?**
# - 假设此时山上的浓雾很大,下山的路无法确定;
# - 假设你摔不死!
#
# - 你只能利用自己周围的信息去找到下山的路径。
# - 以你当前的位置为基准,寻找这个位置最陡峭的方向,从这个方向向下走。
#
#
#
#
# **如何找到最快下山的路?**
# - 假设此时山上的浓雾很大,下山的路无法确定;
# - 假设你摔不死!
#
# - 你只能利用自己周围的信息去找到下山的路径。
# - 以你当前的位置为基准,寻找这个位置最陡峭的方向,从这个方向向下走。
#
#  # **Gradient is the vector of partial derivatives**
#
# One approach to maximizing a function is to
# - pick a random starting point,
# - compute the gradient,
# - take a small step in the direction of the gradient, and
# - repeat with a new staring point.
#
#
#
#
#
# **Gradient is the vector of partial derivatives**
#
# One approach to maximizing a function is to
# - pick a random starting point,
# - compute the gradient,
# - take a small step in the direction of the gradient, and
# - repeat with a new staring point.
#
#
#
#
# 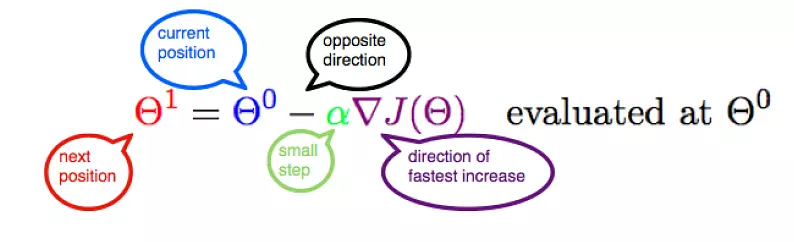 # Let's represent parameters as $\Theta$, learning rate as $\alpha$, and gradient as $\bigtriangledown J(\Theta)$,
# To the find the best model is an optimization problem
# - “minimizes the error of the model”
# - “maximizes the likelihood of the data.”
# We’ll frequently need to maximize (or minimize) functions.
# - to find the input vector v that produces the largest (or smallest) possible value.
#
# # Mathematics behind Gradient Descent
#
# A simple mathematical intuition behind one of the commonly used optimisation algorithms in Machine Learning.
#
# https://www.douban.com/note/713353797/
# The cost or loss function:
#
# $$Cost = \frac{1}{N} \sum_{i = 1}^N (Y' -Y)^2$$
#
#
#
# Let's represent parameters as $\Theta$, learning rate as $\alpha$, and gradient as $\bigtriangledown J(\Theta)$,
# To the find the best model is an optimization problem
# - “minimizes the error of the model”
# - “maximizes the likelihood of the data.”
# We’ll frequently need to maximize (or minimize) functions.
# - to find the input vector v that produces the largest (or smallest) possible value.
#
# # Mathematics behind Gradient Descent
#
# A simple mathematical intuition behind one of the commonly used optimisation algorithms in Machine Learning.
#
# https://www.douban.com/note/713353797/
# The cost or loss function:
#
# $$Cost = \frac{1}{N} \sum_{i = 1}^N (Y' -Y)^2$$
#
#
#  # Parameters with small changes:
# $$ m_1 = m_0 - \delta m, b_1 = b_0 - \delta b$$
#
# The cost function J is a function of m and b:
#
# $$J_{m, b} = \frac{1}{N} \sum_{i = 1}^N (Y' -Y)^2 = \frac{1}{N} \sum_{i = 1}^N Error_i^2$$
# $$\frac{\partial J}{\partial m} = 2 Error \frac{\partial}{\partial m}Error$$
#
# $$\frac{\partial J}{\partial b} = 2 Error \frac{\partial}{\partial b}Error$$
# Let's fit the data with linear regression:
#
# $$\frac{\partial}{\partial m}Error = \frac{\partial}{\partial m}(Y' - Y) = \frac{\partial}{\partial m}(mX + b - Y)$$
#
# Since $X, b, Y$ are constant:
#
# $$\frac{\partial}{\partial m}Error = X$$
# $$\frac{\partial}{\partial b}Error = \frac{\partial}{\partial b}(Y' - Y) = \frac{\partial}{\partial b}(mX + b - Y)$$
#
# Since $X, m, Y$ are constant:
#
# $$\frac{\partial}{\partial m}Error = 1$$
# Thus:
#
# $$\frac{\partial J}{\partial m} = 2 * Error * X$$
# $$\frac{\partial J}{\partial b} = 2 * Error$$
# Let's get rid of the constant 2 and multiplying the learning rate $\alpha$, who determines how large a step to take:
#
# $$\frac{\partial J}{\partial m} = Error * X * \alpha$$
# $$\frac{\partial J}{\partial b} = Error * \alpha$$
#
# Since $ m_1 = m_0 - \delta m, b_1 = b_0 - \delta b$:
#
# $$ m_1 = m_0 - Error * X * \alpha$$
#
# $$b_1 = b_0 - Error * \alpha$$
#
# **Notice** that the slope b can be viewed as the beta value for X = 1. Thus, the above two equations are in essence the same.
#
# Let's represent parameters as $\Theta$, learning rate as $\alpha$, and gradient as $\bigtriangledown J(\Theta)$, we have:
#
#
# $$\Theta_1 = \Theta_0 - \alpha \bigtriangledown J(\Theta)$$
#
#
#
#
# Parameters with small changes:
# $$ m_1 = m_0 - \delta m, b_1 = b_0 - \delta b$$
#
# The cost function J is a function of m and b:
#
# $$J_{m, b} = \frac{1}{N} \sum_{i = 1}^N (Y' -Y)^2 = \frac{1}{N} \sum_{i = 1}^N Error_i^2$$
# $$\frac{\partial J}{\partial m} = 2 Error \frac{\partial}{\partial m}Error$$
#
# $$\frac{\partial J}{\partial b} = 2 Error \frac{\partial}{\partial b}Error$$
# Let's fit the data with linear regression:
#
# $$\frac{\partial}{\partial m}Error = \frac{\partial}{\partial m}(Y' - Y) = \frac{\partial}{\partial m}(mX + b - Y)$$
#
# Since $X, b, Y$ are constant:
#
# $$\frac{\partial}{\partial m}Error = X$$
# $$\frac{\partial}{\partial b}Error = \frac{\partial}{\partial b}(Y' - Y) = \frac{\partial}{\partial b}(mX + b - Y)$$
#
# Since $X, m, Y$ are constant:
#
# $$\frac{\partial}{\partial m}Error = 1$$
# Thus:
#
# $$\frac{\partial J}{\partial m} = 2 * Error * X$$
# $$\frac{\partial J}{\partial b} = 2 * Error$$
# Let's get rid of the constant 2 and multiplying the learning rate $\alpha$, who determines how large a step to take:
#
# $$\frac{\partial J}{\partial m} = Error * X * \alpha$$
# $$\frac{\partial J}{\partial b} = Error * \alpha$$
#
# Since $ m_1 = m_0 - \delta m, b_1 = b_0 - \delta b$:
#
# $$ m_1 = m_0 - Error * X * \alpha$$
#
# $$b_1 = b_0 - Error * \alpha$$
#
# **Notice** that the slope b can be viewed as the beta value for X = 1. Thus, the above two equations are in essence the same.
#
# Let's represent parameters as $\Theta$, learning rate as $\alpha$, and gradient as $\bigtriangledown J(\Theta)$, we have:
#
#
# $$\Theta_1 = \Theta_0 - \alpha \bigtriangledown J(\Theta)$$
#
#
#
#  # Hence,to solve for the gradient, we iterate through our data points using our new $m$ and $b$ values and compute the partial derivatives.
#
# This new gradient tells us
# - the slope of our cost function at our current position
# - the direction we should move to update our parameters.
#
# - The size of our update is controlled by the learning rate.
# In[17]:
import numpy as np
# Size of the points dataset.
m = 20
# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))
# Points y-coordinate
y = np.array([3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21]).reshape(m, 1)
# The Learning Rate alpha.
alpha = 0.01
# In[18]:
def error_function(theta, X, y):
'''Error function J definition.'''
diff = np.dot(X, theta) - y
return (1./2*m) * np.dot(np.transpose(diff), diff)
def gradient_function(theta, X, y):
'''Gradient of the function J definition.'''
diff = np.dot(X, theta) - y
return (1./m) * np.dot(np.transpose(X), diff)
def gradient_descent(X, y, alpha):
'''Perform gradient descent.'''
theta = np.array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, y)
while not np.all(np.absolute(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, y)
return theta
# source:https://www.jianshu.com/p/c7e642877b0e
# In[23]:
optimal = gradient_descent(X, y, alpha)
print('Optimal parameters Theta:', optimal[0][0], optimal[1][0])
print('Error function:', error_function(optimal, X, y)[0,0])
# # This is the End!
# # Estimating the Gradient
# If f is a function of one variable, its derivative at a point x measures how f(x) changes when we make a very small change to x.
#
# > It is defined as the limit of the difference quotients:
#
#
# 差商(difference quotient)就是因变量的改变量与自变量的改变量两者相除的商。
# In[2]:
def difference_quotient(f, x, h):
return (f(x + h) - f(x)) / h
# For many functions it’s easy to exactly calculate derivatives.
#
# For example, the square function:
#
# def square(x):
# return x * x
#
# has the derivative:
#
# def derivative(x):
# return 2 * x
# In[3]:
def square(x):
return x * x
def derivative(x):
return 2 * x
derivative_estimate = lambda x: difference_quotient(square, x, h=0.00001)
# In[9]:
def sum_of_squares(v):
"""computes the sum of squared elements in v"""
return sum(v_i ** 2 for v_i in v)
# In[12]:
# plot to show they're basically the same
import matplotlib.pyplot as plt
x = range(-10,10)
plt.plot(x, list(map(derivative, x)), 'rx') # red x
plt.plot(x, list(map(derivative_estimate, x)), 'b+') # blue +
plt.show()
# When f is a function of many variables, it has multiple partial derivatives.
# In[5]:
def partial_difference_quotient(f, v, i, h):
# add h to just the i-th element of v
w = [v_j + (h if j == i else 0)
for j, v_j in enumerate(v)]
return (f(w) - f(v)) / h
def estimate_gradient(f, v, h=0.00001):
return [partial_difference_quotient(f, v, i, h)
for i, _ in enumerate(v)]
# # Using the Gradient
# In[6]:
def step(v, direction, step_size):
"""move step_size in the direction from v"""
return [v_i + step_size * direction_i
for v_i, direction_i in zip(v, direction)]
def sum_of_squares_gradient(v):
return [2 * v_i for v_i in v]
# In[38]:
from collections import Counter
from linear_algebra import distance, vector_subtract, scalar_multiply
from functools import reduce
import math, random
# In[42]:
print("using the gradient")
# generate 3 numbers
v = [random.randint(-10,10) for i in range(3)]
print(v)
tolerance = 0.0000001
n = 0
while True:
gradient = sum_of_squares_gradient(v) # compute the gradient at v
if n%50 ==0:
print(v, sum_of_squares(v))
next_v = step(v, gradient, -0.01) # take a negative gradient step
if distance(next_v, v) < tolerance: # stop if we're converging
break
v = next_v # continue if we're not
n += 1
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# # Choosing the Right Step Size
# Although the rationale for moving against the gradient is clear,
# - how far to move is not.
# - Indeed, choosing the right step size is more of an art than a science.
# Methods:
# 1. Using a fixed step size
# 1. Gradually shrinking the step size over time
# 1. At each step, choosing the step size that minimizes the value of the objective function
# In[13]:
step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
# It is possible that certain step sizes will result in invalid inputs for our function.
#
# So we’ll need to create a “safe apply” function
# - returns infinity for invalid inputs:
# - which should never be the minimum of anything
# In[14]:
def safe(f):
"""define a new function that wraps f and return it"""
def safe_f(*args, **kwargs):
try:
return f(*args, **kwargs)
except:
return float('inf') # this means "infinity" in Python
return safe_f
# # Putting It All Together
# - **target_fn** that we want to minimize
# - **gradient_fn**.
#
# For example, the target_fn could represent the errors in a model as a function of its parameters,
#
# To choose a starting value for the parameters `theta_0`.
# In[15]:
def minimize_batch(target_fn, gradient_fn, theta_0, tolerance=0.000001):
"""use gradient descent to find theta that minimizes target function"""
step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
theta = theta_0 # set theta to initial value
target_fn = safe(target_fn) # safe version of target_fn
value = target_fn(theta) # value we're minimizing
while True:
gradient = gradient_fn(theta)
next_thetas = [step(theta, gradient, -step_size)
for step_size in step_sizes]
# choose the one that minimizes the error function
next_theta = min(next_thetas, key=target_fn)
next_value = target_fn(next_theta)
# stop if we're "converging"
if abs(value - next_value) < tolerance:
return theta
else:
theta, value = next_theta, next_value
# In[16]:
# minimize_batch"
v = [random.randint(-10,10) for i in range(3)]
v = minimize_batch(sum_of_squares, sum_of_squares_gradient, v)
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# Sometimes we’ll instead want to maximize a function, which we can do by minimizing its negative
# In[19]:
def negate(f):
"""return a function that for any input x returns -f(x)"""
return lambda *args, **kwargs: -f(*args, **kwargs)
def negate_all(f):
"""the same when f returns a list of numbers"""
return lambda *args, **kwargs: [-y for y in f(*args, **kwargs)]
def maximize_batch(target_fn, gradient_fn, theta_0, tolerance=0.000001):
return minimize_batch(negate(target_fn),
negate_all(gradient_fn),
theta_0,
tolerance)
# Using the batch approach, each gradient step requires us to make a prediction and compute the gradient for the whole data set, which makes each step take a long time.
# Error functions are additive
# - The predictive error on the whole data set is simply the sum of the predictive errors for each data point.
#
# When this is the case, we can instead apply a technique called **stochastic gradient descent**
# - which computes the gradient (and takes a step) for only one point at a time.
# - It cycles over our data repeatedly until it reaches a stopping point.
# # Stochastic Gradient Descent
# During each cycle, we’ll want to iterate through our data in a random order:
# In[20]:
def in_random_order(data):
"""generator that returns the elements of data in random order"""
indexes = [i for i, _ in enumerate(data)] # create a list of indexes
random.shuffle(indexes) # shuffle them
for i in indexes: # return the data in that order
yield data[i]
# This approach avoids circling around near a minimum forever
# - whenever we stop getting improvements we’ll decrease the step size and eventually quit.
# In[25]:
def minimize_stochastic(target_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
data = list(zip(x, y))
theta = theta_0 # initial guess
alpha = alpha_0 # initial step size
min_theta, min_value = None, float("inf") # the minimum so far
iterations_with_no_improvement = 0
# if we ever go 100 iterations with no improvement, stop
while iterations_with_no_improvement < 100:
value = sum( target_fn(x_i, y_i, theta) for x_i, y_i in data )
if value < min_value:
# if we've found a new minimum, remember it
# and go back to the original step size
min_theta, min_value = theta, value
iterations_with_no_improvement = 0
alpha = alpha_0
else:
# otherwise we're not improving, so try shrinking the step size
iterations_with_no_improvement += 1
alpha *= 0.9
# and take a gradient step for each of the data points
for x_i, y_i in in_random_order(data):
gradient_i = gradient_fn(x_i, y_i, theta)
theta = vector_subtract(theta, scalar_multiply(alpha, gradient_i))
return min_theta
# In[26]:
def maximize_stochastic(target_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
return minimize_stochastic(negate(target_fn),
negate_all(gradient_fn),
x, y, theta_0, alpha_0)
# In[ ]:
print("using minimize_stochastic_batch")
x = list(range(101))
y = [3*x_i + random.randint(-10, 20) for x_i in x]
theta_0 = random.randint(-10,10)
v = minimize_stochastic(sum_of_squares, sum_of_squares_gradient, x, y, theta_0)
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# Scikit-learn has a Stochastic Gradient Descent module http://scikit-learn.org/stable/modules/sgd.html
# In[ ]:
# Hence,to solve for the gradient, we iterate through our data points using our new $m$ and $b$ values and compute the partial derivatives.
#
# This new gradient tells us
# - the slope of our cost function at our current position
# - the direction we should move to update our parameters.
#
# - The size of our update is controlled by the learning rate.
# In[17]:
import numpy as np
# Size of the points dataset.
m = 20
# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))
# Points y-coordinate
y = np.array([3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21]).reshape(m, 1)
# The Learning Rate alpha.
alpha = 0.01
# In[18]:
def error_function(theta, X, y):
'''Error function J definition.'''
diff = np.dot(X, theta) - y
return (1./2*m) * np.dot(np.transpose(diff), diff)
def gradient_function(theta, X, y):
'''Gradient of the function J definition.'''
diff = np.dot(X, theta) - y
return (1./m) * np.dot(np.transpose(X), diff)
def gradient_descent(X, y, alpha):
'''Perform gradient descent.'''
theta = np.array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, y)
while not np.all(np.absolute(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, y)
return theta
# source:https://www.jianshu.com/p/c7e642877b0e
# In[23]:
optimal = gradient_descent(X, y, alpha)
print('Optimal parameters Theta:', optimal[0][0], optimal[1][0])
print('Error function:', error_function(optimal, X, y)[0,0])
# # This is the End!
# # Estimating the Gradient
# If f is a function of one variable, its derivative at a point x measures how f(x) changes when we make a very small change to x.
#
# > It is defined as the limit of the difference quotients:
#
#
# 差商(difference quotient)就是因变量的改变量与自变量的改变量两者相除的商。
# In[2]:
def difference_quotient(f, x, h):
return (f(x + h) - f(x)) / h
# For many functions it’s easy to exactly calculate derivatives.
#
# For example, the square function:
#
# def square(x):
# return x * x
#
# has the derivative:
#
# def derivative(x):
# return 2 * x
# In[3]:
def square(x):
return x * x
def derivative(x):
return 2 * x
derivative_estimate = lambda x: difference_quotient(square, x, h=0.00001)
# In[9]:
def sum_of_squares(v):
"""computes the sum of squared elements in v"""
return sum(v_i ** 2 for v_i in v)
# In[12]:
# plot to show they're basically the same
import matplotlib.pyplot as plt
x = range(-10,10)
plt.plot(x, list(map(derivative, x)), 'rx') # red x
plt.plot(x, list(map(derivative_estimate, x)), 'b+') # blue +
plt.show()
# When f is a function of many variables, it has multiple partial derivatives.
# In[5]:
def partial_difference_quotient(f, v, i, h):
# add h to just the i-th element of v
w = [v_j + (h if j == i else 0)
for j, v_j in enumerate(v)]
return (f(w) - f(v)) / h
def estimate_gradient(f, v, h=0.00001):
return [partial_difference_quotient(f, v, i, h)
for i, _ in enumerate(v)]
# # Using the Gradient
# In[6]:
def step(v, direction, step_size):
"""move step_size in the direction from v"""
return [v_i + step_size * direction_i
for v_i, direction_i in zip(v, direction)]
def sum_of_squares_gradient(v):
return [2 * v_i for v_i in v]
# In[38]:
from collections import Counter
from linear_algebra import distance, vector_subtract, scalar_multiply
from functools import reduce
import math, random
# In[42]:
print("using the gradient")
# generate 3 numbers
v = [random.randint(-10,10) for i in range(3)]
print(v)
tolerance = 0.0000001
n = 0
while True:
gradient = sum_of_squares_gradient(v) # compute the gradient at v
if n%50 ==0:
print(v, sum_of_squares(v))
next_v = step(v, gradient, -0.01) # take a negative gradient step
if distance(next_v, v) < tolerance: # stop if we're converging
break
v = next_v # continue if we're not
n += 1
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# # Choosing the Right Step Size
# Although the rationale for moving against the gradient is clear,
# - how far to move is not.
# - Indeed, choosing the right step size is more of an art than a science.
# Methods:
# 1. Using a fixed step size
# 1. Gradually shrinking the step size over time
# 1. At each step, choosing the step size that minimizes the value of the objective function
# In[13]:
step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
# It is possible that certain step sizes will result in invalid inputs for our function.
#
# So we’ll need to create a “safe apply” function
# - returns infinity for invalid inputs:
# - which should never be the minimum of anything
# In[14]:
def safe(f):
"""define a new function that wraps f and return it"""
def safe_f(*args, **kwargs):
try:
return f(*args, **kwargs)
except:
return float('inf') # this means "infinity" in Python
return safe_f
# # Putting It All Together
# - **target_fn** that we want to minimize
# - **gradient_fn**.
#
# For example, the target_fn could represent the errors in a model as a function of its parameters,
#
# To choose a starting value for the parameters `theta_0`.
# In[15]:
def minimize_batch(target_fn, gradient_fn, theta_0, tolerance=0.000001):
"""use gradient descent to find theta that minimizes target function"""
step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
theta = theta_0 # set theta to initial value
target_fn = safe(target_fn) # safe version of target_fn
value = target_fn(theta) # value we're minimizing
while True:
gradient = gradient_fn(theta)
next_thetas = [step(theta, gradient, -step_size)
for step_size in step_sizes]
# choose the one that minimizes the error function
next_theta = min(next_thetas, key=target_fn)
next_value = target_fn(next_theta)
# stop if we're "converging"
if abs(value - next_value) < tolerance:
return theta
else:
theta, value = next_theta, next_value
# In[16]:
# minimize_batch"
v = [random.randint(-10,10) for i in range(3)]
v = minimize_batch(sum_of_squares, sum_of_squares_gradient, v)
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# Sometimes we’ll instead want to maximize a function, which we can do by minimizing its negative
# In[19]:
def negate(f):
"""return a function that for any input x returns -f(x)"""
return lambda *args, **kwargs: -f(*args, **kwargs)
def negate_all(f):
"""the same when f returns a list of numbers"""
return lambda *args, **kwargs: [-y for y in f(*args, **kwargs)]
def maximize_batch(target_fn, gradient_fn, theta_0, tolerance=0.000001):
return minimize_batch(negate(target_fn),
negate_all(gradient_fn),
theta_0,
tolerance)
# Using the batch approach, each gradient step requires us to make a prediction and compute the gradient for the whole data set, which makes each step take a long time.
# Error functions are additive
# - The predictive error on the whole data set is simply the sum of the predictive errors for each data point.
#
# When this is the case, we can instead apply a technique called **stochastic gradient descent**
# - which computes the gradient (and takes a step) for only one point at a time.
# - It cycles over our data repeatedly until it reaches a stopping point.
# # Stochastic Gradient Descent
# During each cycle, we’ll want to iterate through our data in a random order:
# In[20]:
def in_random_order(data):
"""generator that returns the elements of data in random order"""
indexes = [i for i, _ in enumerate(data)] # create a list of indexes
random.shuffle(indexes) # shuffle them
for i in indexes: # return the data in that order
yield data[i]
# This approach avoids circling around near a minimum forever
# - whenever we stop getting improvements we’ll decrease the step size and eventually quit.
# In[25]:
def minimize_stochastic(target_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
data = list(zip(x, y))
theta = theta_0 # initial guess
alpha = alpha_0 # initial step size
min_theta, min_value = None, float("inf") # the minimum so far
iterations_with_no_improvement = 0
# if we ever go 100 iterations with no improvement, stop
while iterations_with_no_improvement < 100:
value = sum( target_fn(x_i, y_i, theta) for x_i, y_i in data )
if value < min_value:
# if we've found a new minimum, remember it
# and go back to the original step size
min_theta, min_value = theta, value
iterations_with_no_improvement = 0
alpha = alpha_0
else:
# otherwise we're not improving, so try shrinking the step size
iterations_with_no_improvement += 1
alpha *= 0.9
# and take a gradient step for each of the data points
for x_i, y_i in in_random_order(data):
gradient_i = gradient_fn(x_i, y_i, theta)
theta = vector_subtract(theta, scalar_multiply(alpha, gradient_i))
return min_theta
# In[26]:
def maximize_stochastic(target_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
return minimize_stochastic(negate(target_fn),
negate_all(gradient_fn),
x, y, theta_0, alpha_0)
# In[ ]:
print("using minimize_stochastic_batch")
x = list(range(101))
y = [3*x_i + random.randint(-10, 20) for x_i in x]
theta_0 = random.randint(-10,10)
v = minimize_stochastic(sum_of_squares, sum_of_squares_gradient, x, y, theta_0)
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# Scikit-learn has a Stochastic Gradient Descent module http://scikit-learn.org/stable/modules/sgd.html
# In[ ]:
 #
#  #
#
# **如何找到最快下山的路?**
# - 假设此时山上的浓雾很大,下山的路无法确定;
# - 假设你摔不死!
#
# - 你只能利用自己周围的信息去找到下山的路径。
# - 以你当前的位置为基准,寻找这个位置最陡峭的方向,从这个方向向下走。
#
#
#
#
# **如何找到最快下山的路?**
# - 假设此时山上的浓雾很大,下山的路无法确定;
# - 假设你摔不死!
#
# - 你只能利用自己周围的信息去找到下山的路径。
# - 以你当前的位置为基准,寻找这个位置最陡峭的方向,从这个方向向下走。
#
#  # **Gradient is the vector of partial derivatives**
#
# One approach to maximizing a function is to
# - pick a random starting point,
# - compute the gradient,
# - take a small step in the direction of the gradient, and
# - repeat with a new staring point.
#
#
#
#
#
# **Gradient is the vector of partial derivatives**
#
# One approach to maximizing a function is to
# - pick a random starting point,
# - compute the gradient,
# - take a small step in the direction of the gradient, and
# - repeat with a new staring point.
#
#
#
#
#  # Let's represent parameters as $\Theta$, learning rate as $\alpha$, and gradient as $\bigtriangledown J(\Theta)$,
# To the find the best model is an optimization problem
# - “minimizes the error of the model”
# - “maximizes the likelihood of the data.”
# We’ll frequently need to maximize (or minimize) functions.
# - to find the input vector v that produces the largest (or smallest) possible value.
#
# # Mathematics behind Gradient Descent
#
# A simple mathematical intuition behind one of the commonly used optimisation algorithms in Machine Learning.
#
# https://www.douban.com/note/713353797/
# The cost or loss function:
#
# $$Cost = \frac{1}{N} \sum_{i = 1}^N (Y' -Y)^2$$
#
#
#
# Let's represent parameters as $\Theta$, learning rate as $\alpha$, and gradient as $\bigtriangledown J(\Theta)$,
# To the find the best model is an optimization problem
# - “minimizes the error of the model”
# - “maximizes the likelihood of the data.”
# We’ll frequently need to maximize (or minimize) functions.
# - to find the input vector v that produces the largest (or smallest) possible value.
#
# # Mathematics behind Gradient Descent
#
# A simple mathematical intuition behind one of the commonly used optimisation algorithms in Machine Learning.
#
# https://www.douban.com/note/713353797/
# The cost or loss function:
#
# $$Cost = \frac{1}{N} \sum_{i = 1}^N (Y' -Y)^2$$
#
#
#  # Parameters with small changes:
# $$ m_1 = m_0 - \delta m, b_1 = b_0 - \delta b$$
#
# The cost function J is a function of m and b:
#
# $$J_{m, b} = \frac{1}{N} \sum_{i = 1}^N (Y' -Y)^2 = \frac{1}{N} \sum_{i = 1}^N Error_i^2$$
# $$\frac{\partial J}{\partial m} = 2 Error \frac{\partial}{\partial m}Error$$
#
# $$\frac{\partial J}{\partial b} = 2 Error \frac{\partial}{\partial b}Error$$
# Let's fit the data with linear regression:
#
# $$\frac{\partial}{\partial m}Error = \frac{\partial}{\partial m}(Y' - Y) = \frac{\partial}{\partial m}(mX + b - Y)$$
#
# Since $X, b, Y$ are constant:
#
# $$\frac{\partial}{\partial m}Error = X$$
# $$\frac{\partial}{\partial b}Error = \frac{\partial}{\partial b}(Y' - Y) = \frac{\partial}{\partial b}(mX + b - Y)$$
#
# Since $X, m, Y$ are constant:
#
# $$\frac{\partial}{\partial m}Error = 1$$
# Thus:
#
# $$\frac{\partial J}{\partial m} = 2 * Error * X$$
# $$\frac{\partial J}{\partial b} = 2 * Error$$
# Let's get rid of the constant 2 and multiplying the learning rate $\alpha$, who determines how large a step to take:
#
# $$\frac{\partial J}{\partial m} = Error * X * \alpha$$
# $$\frac{\partial J}{\partial b} = Error * \alpha$$
#
# Since $ m_1 = m_0 - \delta m, b_1 = b_0 - \delta b$:
#
# $$ m_1 = m_0 - Error * X * \alpha$$
#
# $$b_1 = b_0 - Error * \alpha$$
#
# **Notice** that the slope b can be viewed as the beta value for X = 1. Thus, the above two equations are in essence the same.
#
# Let's represent parameters as $\Theta$, learning rate as $\alpha$, and gradient as $\bigtriangledown J(\Theta)$, we have:
#
#
# $$\Theta_1 = \Theta_0 - \alpha \bigtriangledown J(\Theta)$$
#
#
#
#
# Parameters with small changes:
# $$ m_1 = m_0 - \delta m, b_1 = b_0 - \delta b$$
#
# The cost function J is a function of m and b:
#
# $$J_{m, b} = \frac{1}{N} \sum_{i = 1}^N (Y' -Y)^2 = \frac{1}{N} \sum_{i = 1}^N Error_i^2$$
# $$\frac{\partial J}{\partial m} = 2 Error \frac{\partial}{\partial m}Error$$
#
# $$\frac{\partial J}{\partial b} = 2 Error \frac{\partial}{\partial b}Error$$
# Let's fit the data with linear regression:
#
# $$\frac{\partial}{\partial m}Error = \frac{\partial}{\partial m}(Y' - Y) = \frac{\partial}{\partial m}(mX + b - Y)$$
#
# Since $X, b, Y$ are constant:
#
# $$\frac{\partial}{\partial m}Error = X$$
# $$\frac{\partial}{\partial b}Error = \frac{\partial}{\partial b}(Y' - Y) = \frac{\partial}{\partial b}(mX + b - Y)$$
#
# Since $X, m, Y$ are constant:
#
# $$\frac{\partial}{\partial m}Error = 1$$
# Thus:
#
# $$\frac{\partial J}{\partial m} = 2 * Error * X$$
# $$\frac{\partial J}{\partial b} = 2 * Error$$
# Let's get rid of the constant 2 and multiplying the learning rate $\alpha$, who determines how large a step to take:
#
# $$\frac{\partial J}{\partial m} = Error * X * \alpha$$
# $$\frac{\partial J}{\partial b} = Error * \alpha$$
#
# Since $ m_1 = m_0 - \delta m, b_1 = b_0 - \delta b$:
#
# $$ m_1 = m_0 - Error * X * \alpha$$
#
# $$b_1 = b_0 - Error * \alpha$$
#
# **Notice** that the slope b can be viewed as the beta value for X = 1. Thus, the above two equations are in essence the same.
#
# Let's represent parameters as $\Theta$, learning rate as $\alpha$, and gradient as $\bigtriangledown J(\Theta)$, we have:
#
#
# $$\Theta_1 = \Theta_0 - \alpha \bigtriangledown J(\Theta)$$
#
#
#
#  # Hence,to solve for the gradient, we iterate through our data points using our new $m$ and $b$ values and compute the partial derivatives.
#
# This new gradient tells us
# - the slope of our cost function at our current position
# - the direction we should move to update our parameters.
#
# - The size of our update is controlled by the learning rate.
# In[17]:
import numpy as np
# Size of the points dataset.
m = 20
# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))
# Points y-coordinate
y = np.array([3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21]).reshape(m, 1)
# The Learning Rate alpha.
alpha = 0.01
# In[18]:
def error_function(theta, X, y):
'''Error function J definition.'''
diff = np.dot(X, theta) - y
return (1./2*m) * np.dot(np.transpose(diff), diff)
def gradient_function(theta, X, y):
'''Gradient of the function J definition.'''
diff = np.dot(X, theta) - y
return (1./m) * np.dot(np.transpose(X), diff)
def gradient_descent(X, y, alpha):
'''Perform gradient descent.'''
theta = np.array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, y)
while not np.all(np.absolute(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, y)
return theta
# source:https://www.jianshu.com/p/c7e642877b0e
# In[23]:
optimal = gradient_descent(X, y, alpha)
print('Optimal parameters Theta:', optimal[0][0], optimal[1][0])
print('Error function:', error_function(optimal, X, y)[0,0])
# # This is the End!
# # Estimating the Gradient
# If f is a function of one variable, its derivative at a point x measures how f(x) changes when we make a very small change to x.
#
# > It is defined as the limit of the difference quotients:
#
#
# 差商(difference quotient)就是因变量的改变量与自变量的改变量两者相除的商。
# In[2]:
def difference_quotient(f, x, h):
return (f(x + h) - f(x)) / h
# For many functions it’s easy to exactly calculate derivatives.
#
# For example, the square function:
#
# def square(x):
# return x * x
#
# has the derivative:
#
# def derivative(x):
# return 2 * x
# In[3]:
def square(x):
return x * x
def derivative(x):
return 2 * x
derivative_estimate = lambda x: difference_quotient(square, x, h=0.00001)
# In[9]:
def sum_of_squares(v):
"""computes the sum of squared elements in v"""
return sum(v_i ** 2 for v_i in v)
# In[12]:
# plot to show they're basically the same
import matplotlib.pyplot as plt
x = range(-10,10)
plt.plot(x, list(map(derivative, x)), 'rx') # red x
plt.plot(x, list(map(derivative_estimate, x)), 'b+') # blue +
plt.show()
# When f is a function of many variables, it has multiple partial derivatives.
# In[5]:
def partial_difference_quotient(f, v, i, h):
# add h to just the i-th element of v
w = [v_j + (h if j == i else 0)
for j, v_j in enumerate(v)]
return (f(w) - f(v)) / h
def estimate_gradient(f, v, h=0.00001):
return [partial_difference_quotient(f, v, i, h)
for i, _ in enumerate(v)]
# # Using the Gradient
# In[6]:
def step(v, direction, step_size):
"""move step_size in the direction from v"""
return [v_i + step_size * direction_i
for v_i, direction_i in zip(v, direction)]
def sum_of_squares_gradient(v):
return [2 * v_i for v_i in v]
# In[38]:
from collections import Counter
from linear_algebra import distance, vector_subtract, scalar_multiply
from functools import reduce
import math, random
# In[42]:
print("using the gradient")
# generate 3 numbers
v = [random.randint(-10,10) for i in range(3)]
print(v)
tolerance = 0.0000001
n = 0
while True:
gradient = sum_of_squares_gradient(v) # compute the gradient at v
if n%50 ==0:
print(v, sum_of_squares(v))
next_v = step(v, gradient, -0.01) # take a negative gradient step
if distance(next_v, v) < tolerance: # stop if we're converging
break
v = next_v # continue if we're not
n += 1
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# # Choosing the Right Step Size
# Although the rationale for moving against the gradient is clear,
# - how far to move is not.
# - Indeed, choosing the right step size is more of an art than a science.
# Methods:
# 1. Using a fixed step size
# 1. Gradually shrinking the step size over time
# 1. At each step, choosing the step size that minimizes the value of the objective function
# In[13]:
step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
# It is possible that certain step sizes will result in invalid inputs for our function.
#
# So we’ll need to create a “safe apply” function
# - returns infinity for invalid inputs:
# - which should never be the minimum of anything
# In[14]:
def safe(f):
"""define a new function that wraps f and return it"""
def safe_f(*args, **kwargs):
try:
return f(*args, **kwargs)
except:
return float('inf') # this means "infinity" in Python
return safe_f
# # Putting It All Together
# - **target_fn** that we want to minimize
# - **gradient_fn**.
#
# For example, the target_fn could represent the errors in a model as a function of its parameters,
#
# To choose a starting value for the parameters `theta_0`.
# In[15]:
def minimize_batch(target_fn, gradient_fn, theta_0, tolerance=0.000001):
"""use gradient descent to find theta that minimizes target function"""
step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
theta = theta_0 # set theta to initial value
target_fn = safe(target_fn) # safe version of target_fn
value = target_fn(theta) # value we're minimizing
while True:
gradient = gradient_fn(theta)
next_thetas = [step(theta, gradient, -step_size)
for step_size in step_sizes]
# choose the one that minimizes the error function
next_theta = min(next_thetas, key=target_fn)
next_value = target_fn(next_theta)
# stop if we're "converging"
if abs(value - next_value) < tolerance:
return theta
else:
theta, value = next_theta, next_value
# In[16]:
# minimize_batch"
v = [random.randint(-10,10) for i in range(3)]
v = minimize_batch(sum_of_squares, sum_of_squares_gradient, v)
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# Sometimes we’ll instead want to maximize a function, which we can do by minimizing its negative
# In[19]:
def negate(f):
"""return a function that for any input x returns -f(x)"""
return lambda *args, **kwargs: -f(*args, **kwargs)
def negate_all(f):
"""the same when f returns a list of numbers"""
return lambda *args, **kwargs: [-y for y in f(*args, **kwargs)]
def maximize_batch(target_fn, gradient_fn, theta_0, tolerance=0.000001):
return minimize_batch(negate(target_fn),
negate_all(gradient_fn),
theta_0,
tolerance)
# Using the batch approach, each gradient step requires us to make a prediction and compute the gradient for the whole data set, which makes each step take a long time.
# Error functions are additive
# - The predictive error on the whole data set is simply the sum of the predictive errors for each data point.
#
# When this is the case, we can instead apply a technique called **stochastic gradient descent**
# - which computes the gradient (and takes a step) for only one point at a time.
# - It cycles over our data repeatedly until it reaches a stopping point.
# # Stochastic Gradient Descent
# During each cycle, we’ll want to iterate through our data in a random order:
# In[20]:
def in_random_order(data):
"""generator that returns the elements of data in random order"""
indexes = [i for i, _ in enumerate(data)] # create a list of indexes
random.shuffle(indexes) # shuffle them
for i in indexes: # return the data in that order
yield data[i]
# This approach avoids circling around near a minimum forever
# - whenever we stop getting improvements we’ll decrease the step size and eventually quit.
# In[25]:
def minimize_stochastic(target_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
data = list(zip(x, y))
theta = theta_0 # initial guess
alpha = alpha_0 # initial step size
min_theta, min_value = None, float("inf") # the minimum so far
iterations_with_no_improvement = 0
# if we ever go 100 iterations with no improvement, stop
while iterations_with_no_improvement < 100:
value = sum( target_fn(x_i, y_i, theta) for x_i, y_i in data )
if value < min_value:
# if we've found a new minimum, remember it
# and go back to the original step size
min_theta, min_value = theta, value
iterations_with_no_improvement = 0
alpha = alpha_0
else:
# otherwise we're not improving, so try shrinking the step size
iterations_with_no_improvement += 1
alpha *= 0.9
# and take a gradient step for each of the data points
for x_i, y_i in in_random_order(data):
gradient_i = gradient_fn(x_i, y_i, theta)
theta = vector_subtract(theta, scalar_multiply(alpha, gradient_i))
return min_theta
# In[26]:
def maximize_stochastic(target_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
return minimize_stochastic(negate(target_fn),
negate_all(gradient_fn),
x, y, theta_0, alpha_0)
# In[ ]:
print("using minimize_stochastic_batch")
x = list(range(101))
y = [3*x_i + random.randint(-10, 20) for x_i in x]
theta_0 = random.randint(-10,10)
v = minimize_stochastic(sum_of_squares, sum_of_squares_gradient, x, y, theta_0)
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# Scikit-learn has a Stochastic Gradient Descent module http://scikit-learn.org/stable/modules/sgd.html
# In[ ]:
# Hence,to solve for the gradient, we iterate through our data points using our new $m$ and $b$ values and compute the partial derivatives.
#
# This new gradient tells us
# - the slope of our cost function at our current position
# - the direction we should move to update our parameters.
#
# - The size of our update is controlled by the learning rate.
# In[17]:
import numpy as np
# Size of the points dataset.
m = 20
# Points x-coordinate and dummy value (x0, x1).
X0 = np.ones((m, 1))
X1 = np.arange(1, m+1).reshape(m, 1)
X = np.hstack((X0, X1))
# Points y-coordinate
y = np.array([3, 4, 5, 5, 2, 4, 7, 8, 11, 8, 12,
11, 13, 13, 16, 17, 18, 17, 19, 21]).reshape(m, 1)
# The Learning Rate alpha.
alpha = 0.01
# In[18]:
def error_function(theta, X, y):
'''Error function J definition.'''
diff = np.dot(X, theta) - y
return (1./2*m) * np.dot(np.transpose(diff), diff)
def gradient_function(theta, X, y):
'''Gradient of the function J definition.'''
diff = np.dot(X, theta) - y
return (1./m) * np.dot(np.transpose(X), diff)
def gradient_descent(X, y, alpha):
'''Perform gradient descent.'''
theta = np.array([1, 1]).reshape(2, 1)
gradient = gradient_function(theta, X, y)
while not np.all(np.absolute(gradient) <= 1e-5):
theta = theta - alpha * gradient
gradient = gradient_function(theta, X, y)
return theta
# source:https://www.jianshu.com/p/c7e642877b0e
# In[23]:
optimal = gradient_descent(X, y, alpha)
print('Optimal parameters Theta:', optimal[0][0], optimal[1][0])
print('Error function:', error_function(optimal, X, y)[0,0])
# # This is the End!
# # Estimating the Gradient
# If f is a function of one variable, its derivative at a point x measures how f(x) changes when we make a very small change to x.
#
# > It is defined as the limit of the difference quotients:
#
#
# 差商(difference quotient)就是因变量的改变量与自变量的改变量两者相除的商。
# In[2]:
def difference_quotient(f, x, h):
return (f(x + h) - f(x)) / h
# For many functions it’s easy to exactly calculate derivatives.
#
# For example, the square function:
#
# def square(x):
# return x * x
#
# has the derivative:
#
# def derivative(x):
# return 2 * x
# In[3]:
def square(x):
return x * x
def derivative(x):
return 2 * x
derivative_estimate = lambda x: difference_quotient(square, x, h=0.00001)
# In[9]:
def sum_of_squares(v):
"""computes the sum of squared elements in v"""
return sum(v_i ** 2 for v_i in v)
# In[12]:
# plot to show they're basically the same
import matplotlib.pyplot as plt
x = range(-10,10)
plt.plot(x, list(map(derivative, x)), 'rx') # red x
plt.plot(x, list(map(derivative_estimate, x)), 'b+') # blue +
plt.show()
# When f is a function of many variables, it has multiple partial derivatives.
# In[5]:
def partial_difference_quotient(f, v, i, h):
# add h to just the i-th element of v
w = [v_j + (h if j == i else 0)
for j, v_j in enumerate(v)]
return (f(w) - f(v)) / h
def estimate_gradient(f, v, h=0.00001):
return [partial_difference_quotient(f, v, i, h)
for i, _ in enumerate(v)]
# # Using the Gradient
# In[6]:
def step(v, direction, step_size):
"""move step_size in the direction from v"""
return [v_i + step_size * direction_i
for v_i, direction_i in zip(v, direction)]
def sum_of_squares_gradient(v):
return [2 * v_i for v_i in v]
# In[38]:
from collections import Counter
from linear_algebra import distance, vector_subtract, scalar_multiply
from functools import reduce
import math, random
# In[42]:
print("using the gradient")
# generate 3 numbers
v = [random.randint(-10,10) for i in range(3)]
print(v)
tolerance = 0.0000001
n = 0
while True:
gradient = sum_of_squares_gradient(v) # compute the gradient at v
if n%50 ==0:
print(v, sum_of_squares(v))
next_v = step(v, gradient, -0.01) # take a negative gradient step
if distance(next_v, v) < tolerance: # stop if we're converging
break
v = next_v # continue if we're not
n += 1
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# # Choosing the Right Step Size
# Although the rationale for moving against the gradient is clear,
# - how far to move is not.
# - Indeed, choosing the right step size is more of an art than a science.
# Methods:
# 1. Using a fixed step size
# 1. Gradually shrinking the step size over time
# 1. At each step, choosing the step size that minimizes the value of the objective function
# In[13]:
step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
# It is possible that certain step sizes will result in invalid inputs for our function.
#
# So we’ll need to create a “safe apply” function
# - returns infinity for invalid inputs:
# - which should never be the minimum of anything
# In[14]:
def safe(f):
"""define a new function that wraps f and return it"""
def safe_f(*args, **kwargs):
try:
return f(*args, **kwargs)
except:
return float('inf') # this means "infinity" in Python
return safe_f
# # Putting It All Together
# - **target_fn** that we want to minimize
# - **gradient_fn**.
#
# For example, the target_fn could represent the errors in a model as a function of its parameters,
#
# To choose a starting value for the parameters `theta_0`.
# In[15]:
def minimize_batch(target_fn, gradient_fn, theta_0, tolerance=0.000001):
"""use gradient descent to find theta that minimizes target function"""
step_sizes = [100, 10, 1, 0.1, 0.01, 0.001, 0.0001, 0.00001]
theta = theta_0 # set theta to initial value
target_fn = safe(target_fn) # safe version of target_fn
value = target_fn(theta) # value we're minimizing
while True:
gradient = gradient_fn(theta)
next_thetas = [step(theta, gradient, -step_size)
for step_size in step_sizes]
# choose the one that minimizes the error function
next_theta = min(next_thetas, key=target_fn)
next_value = target_fn(next_theta)
# stop if we're "converging"
if abs(value - next_value) < tolerance:
return theta
else:
theta, value = next_theta, next_value
# In[16]:
# minimize_batch"
v = [random.randint(-10,10) for i in range(3)]
v = minimize_batch(sum_of_squares, sum_of_squares_gradient, v)
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# Sometimes we’ll instead want to maximize a function, which we can do by minimizing its negative
# In[19]:
def negate(f):
"""return a function that for any input x returns -f(x)"""
return lambda *args, **kwargs: -f(*args, **kwargs)
def negate_all(f):
"""the same when f returns a list of numbers"""
return lambda *args, **kwargs: [-y for y in f(*args, **kwargs)]
def maximize_batch(target_fn, gradient_fn, theta_0, tolerance=0.000001):
return minimize_batch(negate(target_fn),
negate_all(gradient_fn),
theta_0,
tolerance)
# Using the batch approach, each gradient step requires us to make a prediction and compute the gradient for the whole data set, which makes each step take a long time.
# Error functions are additive
# - The predictive error on the whole data set is simply the sum of the predictive errors for each data point.
#
# When this is the case, we can instead apply a technique called **stochastic gradient descent**
# - which computes the gradient (and takes a step) for only one point at a time.
# - It cycles over our data repeatedly until it reaches a stopping point.
# # Stochastic Gradient Descent
# During each cycle, we’ll want to iterate through our data in a random order:
# In[20]:
def in_random_order(data):
"""generator that returns the elements of data in random order"""
indexes = [i for i, _ in enumerate(data)] # create a list of indexes
random.shuffle(indexes) # shuffle them
for i in indexes: # return the data in that order
yield data[i]
# This approach avoids circling around near a minimum forever
# - whenever we stop getting improvements we’ll decrease the step size and eventually quit.
# In[25]:
def minimize_stochastic(target_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
data = list(zip(x, y))
theta = theta_0 # initial guess
alpha = alpha_0 # initial step size
min_theta, min_value = None, float("inf") # the minimum so far
iterations_with_no_improvement = 0
# if we ever go 100 iterations with no improvement, stop
while iterations_with_no_improvement < 100:
value = sum( target_fn(x_i, y_i, theta) for x_i, y_i in data )
if value < min_value:
# if we've found a new minimum, remember it
# and go back to the original step size
min_theta, min_value = theta, value
iterations_with_no_improvement = 0
alpha = alpha_0
else:
# otherwise we're not improving, so try shrinking the step size
iterations_with_no_improvement += 1
alpha *= 0.9
# and take a gradient step for each of the data points
for x_i, y_i in in_random_order(data):
gradient_i = gradient_fn(x_i, y_i, theta)
theta = vector_subtract(theta, scalar_multiply(alpha, gradient_i))
return min_theta
# In[26]:
def maximize_stochastic(target_fn, gradient_fn, x, y, theta_0, alpha_0=0.01):
return minimize_stochastic(negate(target_fn),
negate_all(gradient_fn),
x, y, theta_0, alpha_0)
# In[ ]:
print("using minimize_stochastic_batch")
x = list(range(101))
y = [3*x_i + random.randint(-10, 20) for x_i in x]
theta_0 = random.randint(-10,10)
v = minimize_stochastic(sum_of_squares, sum_of_squares_gradient, x, y, theta_0)
print("minimum v", v)
print("minimum value", sum_of_squares(v))
# Scikit-learn has a Stochastic Gradient Descent module http://scikit-learn.org/stable/modules/sgd.html
# In[ ]: