#!/usr/bin/env python
# coding: utf-8
# # Trees
#  #
# http://openbookproject.net/thinkcs/python/english3e/trees.html
# - like linked lists, trees are made up of nodes
#
# ## Binary Tree
# - is a commonly used tree in which each node contains a reference to atmost two other nodes (possibly None)
# - these references are referred to as the left and right subtrees
# - like the node of linked list, each node also contains data/cargo
# - like linked lists, trees are recursive data structures that are defined recursively:
# 1. the empty tree, represented by None, or
# 2. a node that contains a data and two tree references (left and right subtree)
# ## Building trees
# - similar to building linked-list
# In[1]:
class Tree:
def __init__(self, data, left=None, right=None):
self.cargo = data
self.left = left
self.right = right
def __str__(self):
return "{}".format(self.cargo)
# ### bottom-up way to build-trees
# - first create children and link them to the parent
# In[4]:
left = Tree(2)
right = Tree(3)
tree = Tree(1, left, right)
# In[5]:
tree1 = Tree(10, Tree(20), Tree(30))
# In[6]:
print(tree)
# In[7]:
print(tree1)
# ## traversing tree
# - natural way to traverse a tree is recursively!
# In[8]:
def findSum(tree):
if not tree:
return 0
return tree.cargo + findSum(tree.left) + findSum(tree.right)
# In[9]:
findSum(tree)
# In[10]:
findSum(tree1)
# ## Expression trees
# - trees are natural way to represent the structure of an expression unambigigously.
# - infix expression 1 + 2 * 3 is ambigious unless we know the order of operation that * happens before +
# - we can use tree to represent the same expression
# - operands are leaf nodes
# - operator nodes contain references to their operands; operators are binary (two operands)
#
#
#
# http://openbookproject.net/thinkcs/python/english3e/trees.html
# - like linked lists, trees are made up of nodes
#
# ## Binary Tree
# - is a commonly used tree in which each node contains a reference to atmost two other nodes (possibly None)
# - these references are referred to as the left and right subtrees
# - like the node of linked list, each node also contains data/cargo
# - like linked lists, trees are recursive data structures that are defined recursively:
# 1. the empty tree, represented by None, or
# 2. a node that contains a data and two tree references (left and right subtree)
# ## Building trees
# - similar to building linked-list
# In[1]:
class Tree:
def __init__(self, data, left=None, right=None):
self.cargo = data
self.left = left
self.right = right
def __str__(self):
return "{}".format(self.cargo)
# ### bottom-up way to build-trees
# - first create children and link them to the parent
# In[4]:
left = Tree(2)
right = Tree(3)
tree = Tree(1, left, right)
# In[5]:
tree1 = Tree(10, Tree(20), Tree(30))
# In[6]:
print(tree)
# In[7]:
print(tree1)
# ## traversing tree
# - natural way to traverse a tree is recursively!
# In[8]:
def findSum(tree):
if not tree:
return 0
return tree.cargo + findSum(tree.left) + findSum(tree.right)
# In[9]:
findSum(tree)
# In[10]:
findSum(tree1)
# ## Expression trees
# - trees are natural way to represent the structure of an expression unambigigously.
# - infix expression 1 + 2 * 3 is ambigious unless we know the order of operation that * happens before +
# - we can use tree to represent the same expression
# - operands are leaf nodes
# - operator nodes contain references to their operands; operators are binary (two operands)
#
# 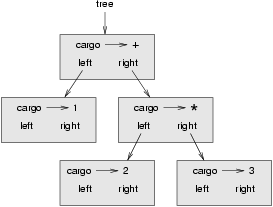 #
# - applications:
# - translate expressions to postfix, prefix, and infix
# - compilers use expression trees to parse, optimize, and translate programs
#
# - three ways to traverse trees: pre-order, in-order and post-order
# In[18]:
expression = Tree('+', Tree(1), Tree('*', Tree(2), Tree(3)))
# ### pre-order tree traversal
# - contents of the root appear before the contents of the children
# - recursive algorithm:
# - visit the node
# - visit left subtree
# - visit right subtree
# In[19]:
def preorder(tree):
if not tree:
return
print(tree.cargo, end=' ')
preorder(tree.left)
preorder(tree.right)
# In[20]:
preorder(expression)
# ### in-order tree traversal
# - contents of the tree appear in order
# - recursive algorithm:
# - visit left subtree
# - visit node
# - visit right subtree
# In[21]:
def inorder(tree):
if not tree:
return
inorder(tree.left)
print(tree.cargo, end=' ')
inorder(tree.right)
# In[22]:
inorder(expression)
# In[29]:
def inorderIndented(tree, level=0):
if not tree:
return
inorderIndented(tree.right, level+1)
print(' '*level + str(tree.cargo))
inorderIndented(tree.left, level+1)
# In[30]:
inorderIndented(expression)
# ### post-order traversal
# - recursive algorithm:
# 1. visit left subtree
# 2. visit right subtree
# 3. visit node
# In[33]:
def postorder(tree):
if not tree:
return
postorder(tree.left)
postorder(tree.right)
print(tree.cargo, end=' ')
# In[34]:
postorder(expression)
# ## building an expression tree
# - parse an infix expression and build the corresponding expression tree
# - e.g., (3 + 7) * 9 yields the following tree:
#
#
# - applications:
# - translate expressions to postfix, prefix, and infix
# - compilers use expression trees to parse, optimize, and translate programs
#
# - three ways to traverse trees: pre-order, in-order and post-order
# In[18]:
expression = Tree('+', Tree(1), Tree('*', Tree(2), Tree(3)))
# ### pre-order tree traversal
# - contents of the root appear before the contents of the children
# - recursive algorithm:
# - visit the node
# - visit left subtree
# - visit right subtree
# In[19]:
def preorder(tree):
if not tree:
return
print(tree.cargo, end=' ')
preorder(tree.left)
preorder(tree.right)
# In[20]:
preorder(expression)
# ### in-order tree traversal
# - contents of the tree appear in order
# - recursive algorithm:
# - visit left subtree
# - visit node
# - visit right subtree
# In[21]:
def inorder(tree):
if not tree:
return
inorder(tree.left)
print(tree.cargo, end=' ')
inorder(tree.right)
# In[22]:
inorder(expression)
# In[29]:
def inorderIndented(tree, level=0):
if not tree:
return
inorderIndented(tree.right, level+1)
print(' '*level + str(tree.cargo))
inorderIndented(tree.left, level+1)
# In[30]:
inorderIndented(expression)
# ### post-order traversal
# - recursive algorithm:
# 1. visit left subtree
# 2. visit right subtree
# 3. visit node
# In[33]:
def postorder(tree):
if not tree:
return
postorder(tree.left)
postorder(tree.right)
print(tree.cargo, end=' ')
# In[34]:
postorder(expression)
# ## building an expression tree
# - parse an infix expression and build the corresponding expression tree
# - e.g., (3 + 7) * 9 yields the following tree:
# 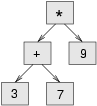 # 1. tokenize expression into python list? How (left as an exercise)
# - (3 + 7) * 9 = ["(", 3, "+", 7, ")", "*", 9, "end"]
# 2. "end" token is useful for preventing the parser from reading pas the end of the list
# In[31]:
def get_token(token_list, expected):
if token_list[0] == expected:
del token_list[0]
return True
return False
# In[36]:
# handles operands
def get_number(token_list):
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None) # leaf node
# In[37]:
token_list = [9, 11, 'end']
x = get_number(token_list)
postorder(x)
# In[38]:
print(token_list)
# In[39]:
def get_product(token_list):
a = get_number(token_list)
if get_token(token_list, '*'):
b = get_number(token_list)
return Tree('*', a, b)
return a
# In[40]:
token_list = [9, '*', 11, 'end']
tree = get_product(token_list)
# In[42]:
postorder(tree)
# In[44]:
token_list = [9, '+', 11, 'end']
tree = get_product(token_list)
postorder(tree)
# In[45]:
# adapt the function for compound product such as 3 * (5 * (7 * 9))
def get_product(token_list):
a = get_number(token_list)
if get_token(token_list, '*'):
b = get_product(token_list)
return Tree('*', a, b)
return a
# In[46]:
token_list = [2, "*", 3, "*", 5 , "*", 7, "end"]
tree = get_product(token_list)
postorder(tree)
# In[47]:
# a sum can be a tree with + at the root, a product on the left, and a sum on the right.
# Or, a sum can be just a product.
def get_sum(token_list):
a = get_product(token_list)
if get_token(token_list, "+"):
b = get_sum(token_list)
return Tree("+", a, b)
return a
# In[48]:
token_list = [9, "*", 11, "+", 5, "*", 7, "end"]
tree = get_sum(token_list)
# In[49]:
postorder(tree)
# In[52]:
# handle parenthesis
def get_number(token_list):
if get_token(token_list, "("):
x = get_sum(token_list) # Get the subexpression
get_token(token_list, ")") # Remove the closing parenthesis
return x
else:
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None)
# In[53]:
# 9 * (11 + 5) * 7
token_list = [9, "*", "(", 11, "+", 5, ")", "*", 7, "end"]
tree = get_sum(token_list)
postorder(tree)
# ## handling errors on malformed expressions
# In[54]:
# handle parenthesis
def get_number(token_list):
if get_token(token_list, "("):
x = get_sum(token_list) # Get the subexpression
if not get_token(token_list, ")"): # Remove the closing parenthesis
raise ValueError('Missing close parenthesis!')
return x
else:
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None)
# In[55]:
token_list = [9, "*", "(", 11, "+", 5, "*", 7, "end"]
tree = get_sum(token_list)
postorder(tree)
# ## exercises:
# 1. Modify inorder function so that it puts parentheses around every operator and pair of operands. Is the output correct and unambiguous? Are the parentheses always necessary?
# 2. Write a function that takes an expression string and returns a token list.
# 3. Find other places in the expression tree functions where errors can occur and add appropriate raise statements. Test your code with improperly formed expressions.
# In[ ]:
# 1. tokenize expression into python list? How (left as an exercise)
# - (3 + 7) * 9 = ["(", 3, "+", 7, ")", "*", 9, "end"]
# 2. "end" token is useful for preventing the parser from reading pas the end of the list
# In[31]:
def get_token(token_list, expected):
if token_list[0] == expected:
del token_list[0]
return True
return False
# In[36]:
# handles operands
def get_number(token_list):
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None) # leaf node
# In[37]:
token_list = [9, 11, 'end']
x = get_number(token_list)
postorder(x)
# In[38]:
print(token_list)
# In[39]:
def get_product(token_list):
a = get_number(token_list)
if get_token(token_list, '*'):
b = get_number(token_list)
return Tree('*', a, b)
return a
# In[40]:
token_list = [9, '*', 11, 'end']
tree = get_product(token_list)
# In[42]:
postorder(tree)
# In[44]:
token_list = [9, '+', 11, 'end']
tree = get_product(token_list)
postorder(tree)
# In[45]:
# adapt the function for compound product such as 3 * (5 * (7 * 9))
def get_product(token_list):
a = get_number(token_list)
if get_token(token_list, '*'):
b = get_product(token_list)
return Tree('*', a, b)
return a
# In[46]:
token_list = [2, "*", 3, "*", 5 , "*", 7, "end"]
tree = get_product(token_list)
postorder(tree)
# In[47]:
# a sum can be a tree with + at the root, a product on the left, and a sum on the right.
# Or, a sum can be just a product.
def get_sum(token_list):
a = get_product(token_list)
if get_token(token_list, "+"):
b = get_sum(token_list)
return Tree("+", a, b)
return a
# In[48]:
token_list = [9, "*", 11, "+", 5, "*", 7, "end"]
tree = get_sum(token_list)
# In[49]:
postorder(tree)
# In[52]:
# handle parenthesis
def get_number(token_list):
if get_token(token_list, "("):
x = get_sum(token_list) # Get the subexpression
get_token(token_list, ")") # Remove the closing parenthesis
return x
else:
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None)
# In[53]:
# 9 * (11 + 5) * 7
token_list = [9, "*", "(", 11, "+", 5, ")", "*", 7, "end"]
tree = get_sum(token_list)
postorder(tree)
# ## handling errors on malformed expressions
# In[54]:
# handle parenthesis
def get_number(token_list):
if get_token(token_list, "("):
x = get_sum(token_list) # Get the subexpression
if not get_token(token_list, ")"): # Remove the closing parenthesis
raise ValueError('Missing close parenthesis!')
return x
else:
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None)
# In[55]:
token_list = [9, "*", "(", 11, "+", 5, "*", 7, "end"]
tree = get_sum(token_list)
postorder(tree)
# ## exercises:
# 1. Modify inorder function so that it puts parentheses around every operator and pair of operands. Is the output correct and unambiguous? Are the parentheses always necessary?
# 2. Write a function that takes an expression string and returns a token list.
# 3. Find other places in the expression tree functions where errors can occur and add appropriate raise statements. Test your code with improperly formed expressions.
# In[ ]:
 #
# - applications:
# - translate expressions to postfix, prefix, and infix
# - compilers use expression trees to parse, optimize, and translate programs
#
# - three ways to traverse trees: pre-order, in-order and post-order
# In[18]:
expression = Tree('+', Tree(1), Tree('*', Tree(2), Tree(3)))
# ### pre-order tree traversal
# - contents of the root appear before the contents of the children
# - recursive algorithm:
# - visit the node
# - visit left subtree
# - visit right subtree
# In[19]:
def preorder(tree):
if not tree:
return
print(tree.cargo, end=' ')
preorder(tree.left)
preorder(tree.right)
# In[20]:
preorder(expression)
# ### in-order tree traversal
# - contents of the tree appear in order
# - recursive algorithm:
# - visit left subtree
# - visit node
# - visit right subtree
# In[21]:
def inorder(tree):
if not tree:
return
inorder(tree.left)
print(tree.cargo, end=' ')
inorder(tree.right)
# In[22]:
inorder(expression)
# In[29]:
def inorderIndented(tree, level=0):
if not tree:
return
inorderIndented(tree.right, level+1)
print(' '*level + str(tree.cargo))
inorderIndented(tree.left, level+1)
# In[30]:
inorderIndented(expression)
# ### post-order traversal
# - recursive algorithm:
# 1. visit left subtree
# 2. visit right subtree
# 3. visit node
# In[33]:
def postorder(tree):
if not tree:
return
postorder(tree.left)
postorder(tree.right)
print(tree.cargo, end=' ')
# In[34]:
postorder(expression)
# ## building an expression tree
# - parse an infix expression and build the corresponding expression tree
# - e.g., (3 + 7) * 9 yields the following tree:
#
#
# - applications:
# - translate expressions to postfix, prefix, and infix
# - compilers use expression trees to parse, optimize, and translate programs
#
# - three ways to traverse trees: pre-order, in-order and post-order
# In[18]:
expression = Tree('+', Tree(1), Tree('*', Tree(2), Tree(3)))
# ### pre-order tree traversal
# - contents of the root appear before the contents of the children
# - recursive algorithm:
# - visit the node
# - visit left subtree
# - visit right subtree
# In[19]:
def preorder(tree):
if not tree:
return
print(tree.cargo, end=' ')
preorder(tree.left)
preorder(tree.right)
# In[20]:
preorder(expression)
# ### in-order tree traversal
# - contents of the tree appear in order
# - recursive algorithm:
# - visit left subtree
# - visit node
# - visit right subtree
# In[21]:
def inorder(tree):
if not tree:
return
inorder(tree.left)
print(tree.cargo, end=' ')
inorder(tree.right)
# In[22]:
inorder(expression)
# In[29]:
def inorderIndented(tree, level=0):
if not tree:
return
inorderIndented(tree.right, level+1)
print(' '*level + str(tree.cargo))
inorderIndented(tree.left, level+1)
# In[30]:
inorderIndented(expression)
# ### post-order traversal
# - recursive algorithm:
# 1. visit left subtree
# 2. visit right subtree
# 3. visit node
# In[33]:
def postorder(tree):
if not tree:
return
postorder(tree.left)
postorder(tree.right)
print(tree.cargo, end=' ')
# In[34]:
postorder(expression)
# ## building an expression tree
# - parse an infix expression and build the corresponding expression tree
# - e.g., (3 + 7) * 9 yields the following tree:
#  # 1. tokenize expression into python list? How (left as an exercise)
# - (3 + 7) * 9 = ["(", 3, "+", 7, ")", "*", 9, "end"]
# 2. "end" token is useful for preventing the parser from reading pas the end of the list
# In[31]:
def get_token(token_list, expected):
if token_list[0] == expected:
del token_list[0]
return True
return False
# In[36]:
# handles operands
def get_number(token_list):
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None) # leaf node
# In[37]:
token_list = [9, 11, 'end']
x = get_number(token_list)
postorder(x)
# In[38]:
print(token_list)
# In[39]:
def get_product(token_list):
a = get_number(token_list)
if get_token(token_list, '*'):
b = get_number(token_list)
return Tree('*', a, b)
return a
# In[40]:
token_list = [9, '*', 11, 'end']
tree = get_product(token_list)
# In[42]:
postorder(tree)
# In[44]:
token_list = [9, '+', 11, 'end']
tree = get_product(token_list)
postorder(tree)
# In[45]:
# adapt the function for compound product such as 3 * (5 * (7 * 9))
def get_product(token_list):
a = get_number(token_list)
if get_token(token_list, '*'):
b = get_product(token_list)
return Tree('*', a, b)
return a
# In[46]:
token_list = [2, "*", 3, "*", 5 , "*", 7, "end"]
tree = get_product(token_list)
postorder(tree)
# In[47]:
# a sum can be a tree with + at the root, a product on the left, and a sum on the right.
# Or, a sum can be just a product.
def get_sum(token_list):
a = get_product(token_list)
if get_token(token_list, "+"):
b = get_sum(token_list)
return Tree("+", a, b)
return a
# In[48]:
token_list = [9, "*", 11, "+", 5, "*", 7, "end"]
tree = get_sum(token_list)
# In[49]:
postorder(tree)
# In[52]:
# handle parenthesis
def get_number(token_list):
if get_token(token_list, "("):
x = get_sum(token_list) # Get the subexpression
get_token(token_list, ")") # Remove the closing parenthesis
return x
else:
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None)
# In[53]:
# 9 * (11 + 5) * 7
token_list = [9, "*", "(", 11, "+", 5, ")", "*", 7, "end"]
tree = get_sum(token_list)
postorder(tree)
# ## handling errors on malformed expressions
# In[54]:
# handle parenthesis
def get_number(token_list):
if get_token(token_list, "("):
x = get_sum(token_list) # Get the subexpression
if not get_token(token_list, ")"): # Remove the closing parenthesis
raise ValueError('Missing close parenthesis!')
return x
else:
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None)
# In[55]:
token_list = [9, "*", "(", 11, "+", 5, "*", 7, "end"]
tree = get_sum(token_list)
postorder(tree)
# ## exercises:
# 1. Modify inorder function so that it puts parentheses around every operator and pair of operands. Is the output correct and unambiguous? Are the parentheses always necessary?
# 2. Write a function that takes an expression string and returns a token list.
# 3. Find other places in the expression tree functions where errors can occur and add appropriate raise statements. Test your code with improperly formed expressions.
# In[ ]:
# 1. tokenize expression into python list? How (left as an exercise)
# - (3 + 7) * 9 = ["(", 3, "+", 7, ")", "*", 9, "end"]
# 2. "end" token is useful for preventing the parser from reading pas the end of the list
# In[31]:
def get_token(token_list, expected):
if token_list[0] == expected:
del token_list[0]
return True
return False
# In[36]:
# handles operands
def get_number(token_list):
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None) # leaf node
# In[37]:
token_list = [9, 11, 'end']
x = get_number(token_list)
postorder(x)
# In[38]:
print(token_list)
# In[39]:
def get_product(token_list):
a = get_number(token_list)
if get_token(token_list, '*'):
b = get_number(token_list)
return Tree('*', a, b)
return a
# In[40]:
token_list = [9, '*', 11, 'end']
tree = get_product(token_list)
# In[42]:
postorder(tree)
# In[44]:
token_list = [9, '+', 11, 'end']
tree = get_product(token_list)
postorder(tree)
# In[45]:
# adapt the function for compound product such as 3 * (5 * (7 * 9))
def get_product(token_list):
a = get_number(token_list)
if get_token(token_list, '*'):
b = get_product(token_list)
return Tree('*', a, b)
return a
# In[46]:
token_list = [2, "*", 3, "*", 5 , "*", 7, "end"]
tree = get_product(token_list)
postorder(tree)
# In[47]:
# a sum can be a tree with + at the root, a product on the left, and a sum on the right.
# Or, a sum can be just a product.
def get_sum(token_list):
a = get_product(token_list)
if get_token(token_list, "+"):
b = get_sum(token_list)
return Tree("+", a, b)
return a
# In[48]:
token_list = [9, "*", 11, "+", 5, "*", 7, "end"]
tree = get_sum(token_list)
# In[49]:
postorder(tree)
# In[52]:
# handle parenthesis
def get_number(token_list):
if get_token(token_list, "("):
x = get_sum(token_list) # Get the subexpression
get_token(token_list, ")") # Remove the closing parenthesis
return x
else:
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None)
# In[53]:
# 9 * (11 + 5) * 7
token_list = [9, "*", "(", 11, "+", 5, ")", "*", 7, "end"]
tree = get_sum(token_list)
postorder(tree)
# ## handling errors on malformed expressions
# In[54]:
# handle parenthesis
def get_number(token_list):
if get_token(token_list, "("):
x = get_sum(token_list) # Get the subexpression
if not get_token(token_list, ")"): # Remove the closing parenthesis
raise ValueError('Missing close parenthesis!')
return x
else:
x = token_list[0]
if not isinstance(x, int):
return None
del token_list[0]
return Tree(x, None, None)
# In[55]:
token_list = [9, "*", "(", 11, "+", 5, "*", 7, "end"]
tree = get_sum(token_list)
postorder(tree)
# ## exercises:
# 1. Modify inorder function so that it puts parentheses around every operator and pair of operands. Is the output correct and unambiguous? Are the parentheses always necessary?
# 2. Write a function that takes an expression string and returns a token list.
# 3. Find other places in the expression tree functions where errors can occur and add appropriate raise statements. Test your code with improperly formed expressions.
# In[ ]: