#!/usr/bin/env python
# coding: utf-8

# ---   
#  <img align="left" width="75" height="75"  src="https://upload.wikimedia.org/wikipedia/en/c/c8/University_of_the_Punjab_logo.png"> 
# 
# <h1 align="center">Department of Data Science</h1>
# <h1 align="center">Course: Tools and Techniques for Data Science</h1>
# 
# ---
# <h3><div align="right">Instructor: Muhammad Arif Butt, Ph.D.</div></h3>    

# <h1 align="center">Lecture 3.5 (NumPy-05)</h1>

# <a href="https://colab.research.google.com/github/arifpucit/data-science/blob/master/Section-3-Python-for-Data-Scientists/Lec-3.05(NumPy-05-BroadcastingandReshaping).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>

# # _Broadcasting, Reshaping, Sorting and Iterating NumPy Arrays.ipynb_

# <img align="center" width="600" height="600"  src="images/reshapingbroadcasting.png" > 

# In[ ]:





# # Learning agenda of this notebook
# 1. Broadcasting NumPy Arrays
# 2. Reshaping NumPy Arrays
#     - Use `shape` attribute (in-place operation)
#     - Use `np.reshape()` method (shallow copy)
#     - Use `np.resize()` method (deep copy)
#     - Use `ndarray.transpose()` method (shallow copy)
#     - Use `np.swapaxes()`method (shallow copy)
#     - Use `np.flatten()` method (deep copy)
# 3. Sorting Arrays using `np.sort()` Method
# 4. Iterating NumPy Arrays

# In[ ]:


# To install this library in Jupyter notebook
#import sys
#!{sys.executable} -m pip install numpy


# In[1]:


import numpy as np
np.__version__ , np.__path__


# In[ ]:





# ## 1. Broadcasting numPy Arrays
# - Numpy arrays also support **broadcasting**, allowing arithmetic operations between two arrays with different numbers of dimensions but compatible shapes. 
# - Subject to certain constraints, the smaller array is “broadcast” across the larger array so that they have compatible shapes.
# - Two dimensions are compatible when
#     - they are equal, or
#     - one of them is 1

# >**Review of Arithmetic operations with numPy arrays of same shape:**

# In[2]:


import numpy as np
# Create two 1-D arrays each having 4 random integers from 1 to 9
arr1 = np.random.randint(1,50, size=5)
arr2 = np.random.randint(1,10, size=5)
print("arr1: ", arr1)
print("arr2: ", arr2)

# After the operation a new `ndarray` is returned
print("arr1 + arr2 = ",      arr1 + arr2)    
print("arr1 / arr2 = ", arr1 / arr2)    
print("arr1 // arr2 = ",   arr1  // arr2)  
print("arr1 ** arr2 = ",      arr1  ** arr2)   


# In[ ]:





# ### a. Arithmetic of 1-Dimensional Array with a Scalar Value

# In[3]:


# Consider adding a scalar value 'a' to a 1-D numPy array
arr1 = np.array([1, 2, 3, 4])
print("arr1: ", arr1)
print("arr1.shape: ", arr1.shape)
a = 2
print("a: ", a)


# In[4]:


# The scalar value is replicated to match the shape of arr1 before the operation
#   [2  2  2  2] 

arr2 = arr1 + a 
print("arr2: \n", arr2)


# In[ ]:





# ### b. Arithmetic of 2-Dimensional Array with a Scalar Value

# In[5]:


# Consider adding a scalar value 'a' to a 2-D numPy array
arr1 = np.array([[1, 2, 3], [1, 2, 3]])
print("arr1:\n", arr1)
print("arr1.shape: ", arr1.shape)
a = 2
print("a: ", a)


# In[6]:


# The scalar value is replicated to match the shape of arr1 before the operation
#   2  2  2 
#   2  2  2 

arr2 = arr1 + a 
print("arr2: \n", arr2)


# In[ ]:





# ### c. Arithmetic of 1-Dimensional Array with a 2-Dimensional Array

# **Example 1:** Consider adding a 2-D array (3x4) to a 1-D array with 4 values

# In[9]:


arr1 = np.array([[1, 2, 3, 4], [3, 4, 5, 6], [2, 7, 8, 9]])
arr2 = np.array([4, 2, 3, 2])
print("arr1:\n", arr1)
print("arr1.shape: ", arr1.shape)
print("arr2:\n", arr2)
print("arr2.shape: ", arr2.shape)


# In[8]:


# The only row of arr2 is replicated twice before the operation
#   4  2  3  5
#   4  2  3  5
#   4  2  3  5

arr3 = arr1 + arr2 

print("arr3: \n", arr3)


# **Example 2:** Consider adding a 2-D array (4x2) to a 1-D array with 2 values

# In[ ]:


arr1 = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
print("arr1:\n", arr1)
print("arr1.shape: ", arr1.shape)

arr2 = np.array([4, 5])
print("arr2:\n", arr2)
print("arr2.shape: ", arr2.shape)


# In[ ]:


# The only row of arr2 is replicated three times before the operation
#   4  5
#   4  5
#   4  5
#   4  5
arr3 = arr2 + arr1 

print("arr3: \n", arr3)


# ### d. Arithmetic of two 2-Dimensional Arrays

# **Example 1:** Consider adding elements of a 2-D array (2x3) with another 2-D array (3x1)

# In[ ]:


arr1 = np.array([[5, 3, 2],[3, 4, 5], [7, 1, 4]])
print("arr1:\n", arr1)
print("arr1.shape: ", arr1.shape)

arr2 = np.array([[100], [200], [300]])
print("arr2:\n", arr2)
print("arr2.shape: ", arr2.shape)


# In[ ]:


# The only column of arr2 is replicated twice before the operation
#   100   100   100
#   200   200   300
#   300   300   300

arr3 = arr1 + arr2 

print("arr3: \n", arr3)


# **Points to Ponder in Arithmetic and Broadcasting:**
# >- Arithmetic between elements of two numPy arrays works fine if both the arrays are of same shape.
# >- Arithmetic between a numPy array and a scalar value works fine due to broadcasting.
# >- Arithmetic between elements of two numPy arrays with different dimensions will work, if and only if the array with smaller dimension can be replicated to match the shape of other array (as in above examples)

# **Example 1: Broadcast Error**

# In[10]:


# Consider adding a 2-D array (2x3) to a 1-D array with 2 values
arr1 = np.array([[1, 2, 3], [1, 2, 3]])
arr2 = np.array([1,2])
print("arr1:\n", arr1)
print("arr1.shape: ", arr1.shape)
print("arr2:\n", arr2)
print("arr2.shape: ", arr2.shape)


# In[11]:


# Since arr2 cannot be replicated to match the shape of arr1,
# (last dimension of `arr1` i.e., 3 does not match with the first dimension of `arr2` i.e., 2)
# therefore, broadcasting is unsuccessful and will flag an error
arr3 = arr1 + arr2 

print("arr3: \n", arr3)


# In[ ]:





# **Example 2: Broadcast Error**

# In[15]:


# Consider adding a 2-D array (2x3) to a 1-D array with 2 values
arr1 = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
print("arr1:\n", arr1)
print("arr1.shape: ", arr1.shape)


arr2 = np.array([[4], [5], [6], [5]])
print("arr2:\n", arr2)
print("arr2.shape: ", arr2.shape)


# In[16]:


# Since arr2 cannot be replicated to match the shape of arr1,
# (last dimension of `arr1` i.e., 2 does not match with the first dimension of `arr2` i.e., 3)
# therefore, broadcasting is unsuccessful and will flag an error
try:
    arr3 = arr1 + arr2 
    print("arr3: \n", arr3)
except ValueError as e:
    print(e)


# **Example 3: Broadcast Error**

# In[ ]:


arr1 = np.array([[5, 3, 2],[3, 4, 5], [7, 1, 4]])
print("arr1:\n", arr1)
print("arr1.shape: ", arr1.shape)

arr2 = np.array([[100], [200]])
print("arr2:\n", arr2)
print("arr2.shape: ", arr2.shape)


# In[ ]:


# Since arr2 cannot be replicated to match the shape of arr1,
# (last dimension of `arr1` i.e., 3 does not match with the first dimension of `arr2` i.e., 2)
# therefore, broadcasting is unsuccessful and will flag an error
try:
    arr3 = arr1 + arr2 
    print("arr3: \n", arr3)
except ValueError as e:
    print(e)


# ## 2. Reshaping Arrays
# - Reshaping numpy array simply means changing the shape of the given array, shape basically tells the number of elements and dimension of array.
# - By reshaping an array we can add or remove dimensions or change number of elements in each dimension.
# - There are different ways that reshape numPy arrays:
#     - Changing the `shape` attribute (in-place operation)
#     - Use `np.reshape()` method (shallow copy)
#     - Use `np.resize()` method (deep copy)
#     - Use `ndarray.transpose()` method (shallow copy)
#     - Use `np.swapaxes()`method (shallow copy)
#     - Use `ndarray.flatten()` method (deep copy)

# In[ ]:





# In[ ]:





# ### a. Change the `np.shape` Attribute
# - Changing the shape of an `ndarray` is as simple as setting its `shape` attribute. However, the array's size must remain the same.
# - No new array is created, rather the change of shape occurs in-place.

# In[17]:


import numpy as np
arr1 = np.arange(24)
print("arr1:", arr1)
print("Dimensions:", arr1.ndim)
print("Shape:", arr1.shape)
print("Strides:", arr1.strides)


# In[18]:


#Changing the shape attribute (array size must remain same)
arr1.shape = (6, 4)
print("arr1: \n", arr1)
print("Dimensions:", arr1.ndim)
print("Shape:", arr1.shape)
print("Strides:", arr1.strides)


# In[ ]:


#Changing the shape attribute (array size must remain same)
arr1.shape = (2, 4, 3)
print("arr1: \n", arr1)
print("Dimensions:", arr1.ndim)
print("Shape:", arr1.shape)
print("Strides:", arr1.strides)


# ### b. Use the `np.reshape()` Method
# <img align="right" width="400" height="400"  src="images/reshapecf.png" > 
# 
# ```
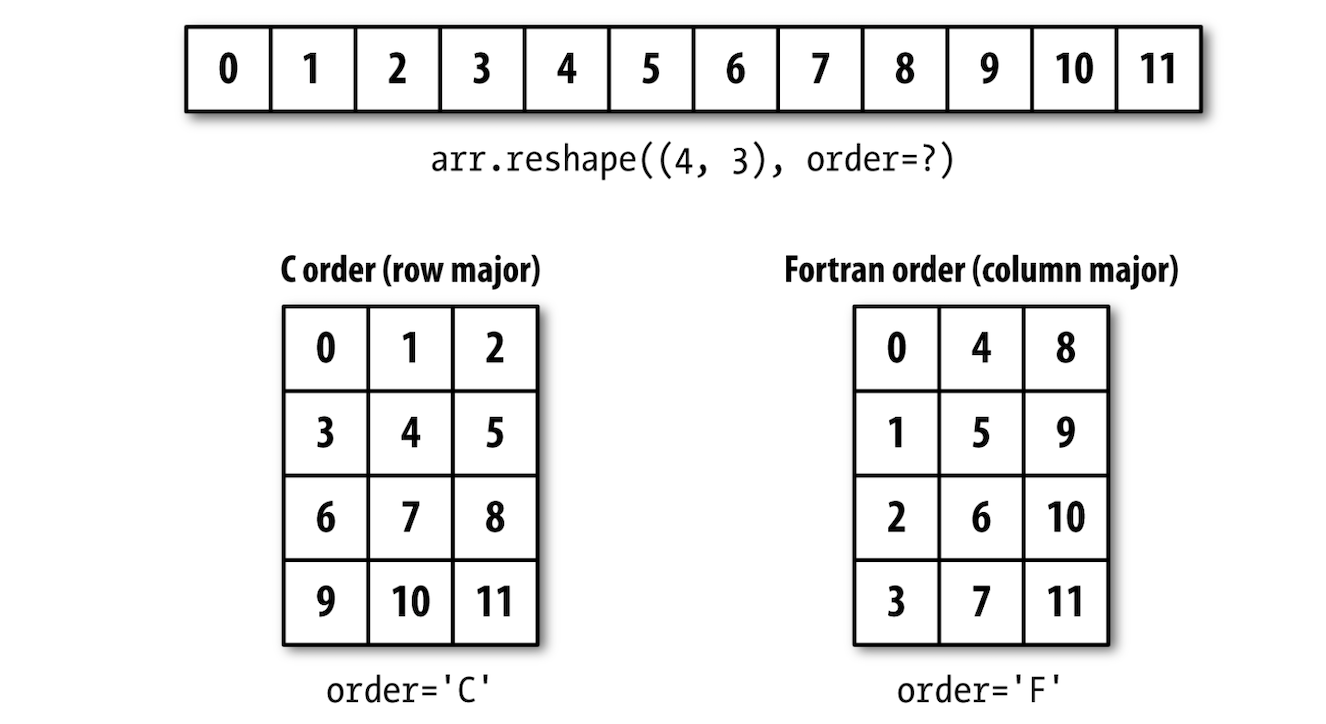# np.reshape(arr, newshape)
# ```
# 
# - The `np.reshape()` method takes the input array, then a tuple that defines the shape of the new array and returns a new array, which shares the same memory as the original array. You can think it as shallow copy in Python, where if you change the data in one array, the corresponding data in the other array is also modified.

# **Example 1:** Reshaping from 1-D numPy Arrays to 2-D numPy Arrays

# In[19]:


arr1 = np.array([1, 2, 3, 4, 5, 6])
print("Original Array: ", arr1, "\nShape: ", arr1.shape)


# In[22]:


# Changing the dimension of array using reshape()
arr2 = np.reshape(arr1, (2, 3))
print("Reshaped Array: \n", arr2, "\nShape: ", arr2.shape)


# In[ ]:


# make change in one of the arrays, the change is reflected in both
arr2[0][0] = 99
print("Original Array: ", arr1)
print("Reshaped Array: \n", arr2)
print("id(arr1): ", id(arr1))
print("id(arr2): ",id(arr2))


# **Example 2:** Reshaping from 1-D numPy Arrays to 3-D numPy Arrays

# In[ ]:


arr1 = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
print("Original Array: ", arr1, "\nShape: ", arr1.shape)

arr2 = np.reshape(arr1, (2, 2, 3))
print("\nReshaped Array: \n", arr2, "\nShape: ", arr2.shape)


# In[ ]:





# **Example 3:** Flattening Arrays. You can convert an array of an unknown dimension to a 1D array using `np.reshape(-1) `

# In[ ]:


arr1 = np.array([[1, 2, 3], [6, 7, 8], [4, 5, 6], [11, 14, 10]])
print("Original Array: \n", arr1, "\nShape: ", arr1.shape)

arr2 = np.reshape(arr1, (-1))
print("\nReshaped Array: \n", arr2, "\nShape: ", arr2.shape)


# **Example 4:** Reshaping an array back to its original dimensions. If you applied the `np.reshape()` method to an array and you want to get the original shape of the array back, you can call the reshape method on that array again.

# In[ ]:


arr1 = np.array([[1, 2, 3], [6, 7, 8], [4, 5, 6], [11, 14, 10]])
print("Original Array: \n", arr1, "\nShape: ", arr1.shape)

arr2 = np.reshape(arr1, (2, 6))
print("\nReshaped Array: \n", arr2, "\nShape: ", arr2.shape)

# covert the array into original shape again
arr3 = np.reshape(arr2, (4,3))
print("\nReshaped to Original Shape: \n", arr3, "\nShape: ", arr3.shape)


# **Example 5:** You can reshape to any shape, the only requirement is that the total elements in both the arrays should be same

# In[ ]:


arr1 = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
arr2 = np.reshape(arr1, (3, 2))
arr2


# ### c.  Use `np.resize()` Method
# ```
# np.resize(arr, newshape)
# ```
# - Like `np.reshape()` method, the `np.resize()` method also takes the input array and a tuple that defines the shape of the array, with one main difference and that is:
#     - If the `newshape` argument mismatch with the size of `arr`, it do not raise error. The new array is formed from the data in the old array, repeated if necessary to fill out the required number of elements.  

# **Example 1:** Resizing from 1-D numPy Arrays to 2-D numPy Arrays. The new array doesn’t share the same memory with the original array. The data change in one array is not mapped to the other.

# In[23]:


arr1 = np.array([1, 2, 3, 4, 5, 6])
print("Original Array: ", arr1, "\nShape: ", arr1.shape)


# In[25]:


# Changing the dimension of array using reshape()
arr2 = np.resize(arr1, (2, 3))
print("Resized Array: \n", arr2, "\nShape: ", arr2.shape)


# In[26]:


# make change in one of the arrays, the change is NOT reflected in both
arr2[0][0] = 99
print("Original Array: ", arr1)
print("Resized Array: \n", arr2)
print("id(arr1): ", id(arr1))
print("id(arr2): ",id(arr2))


# **Example 2:** The `np.resize()` method allows you to resize an array to a new array having larger size than the original array. In this scenario, it fills the remaining array with repeated copies of original array elements

# In[ ]:


arr1 = np.array([1, 2, 3, 4, 5, 6])
print("Original Array: ", arr1, "\nShape: ", arr1.shape)


# In[ ]:


arr2 = np.resize(arr1, (4,4))
print("\nResized Array: \n", arr2, "\nShape: ", arr2.shape)


# In[ ]:





# In[ ]:





# **Example 3:** The `np.resize()` method allows you to resize an array to a new array having smaller size than the original array.

# In[ ]:


arr1 = np.array([1, 2, 3, 4, 5, 6, 7, 8])
print("Original Array: ", arr1, "\nShape: ", arr1.shape)


# In[ ]:


arr2 = np.resize(arr1, (3, 2))
print("\nResized Array: \n", arr2, "\nShape: ", arr2.shape)


# ### d. The `ndarray.transpose()` Method
# ```
# ndarray.transpose()
# ```
# - It has no impact on 1-D array
# - For a 2-D array, this is a standard matrix transpose.
# - For an n-D array, if axes are given, their order indicates how the axes are permuted
# - Returns a view of the array with axes transposed, so this is an in-place operation.

# In[ ]:


arr1 = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print("Original Array: \n", arr1, "\nShape: ", arr1.shape)

#Reshape array using transpose method
arr2 = arr1.transpose()
print("\nTransposed array: \n", arr2,  "\nShape: ", arr2.shape)

## make change in one of the arrays, the change is reflected in both
arr2[1][1] = 99
print("\nOriginal Array: \n", arr1)
print("Transposed Array: \n", arr2)


# ### e. The `np.swapaxes()` Method
# - The `np.swapaxes()` method is used to interchange two axes of an array.
# ```
# np.swapaxes(arr, axis1, axis2)
# ```
#     - `arr`: Input array whose axes are to be swapped
#     - `axis1`: First axis
#     - `axis2`: Second axis
# 
# - For NumPy >= 1.10.0, if `arr` is an ndarray, then a view of `arr` is returned.

# **Example 1:** Swapping axes of a 2-D array

# In[ ]:


arr1 = np.arange(8).reshape(2,4) 
print("Original Array: \n", arr1, "\nShape: ", arr1.shape)


# In[ ]:


#Reshape array using swapaxes() method
arr2 = np.swapaxes(arr1,0, 1)
print("\nNew array: \n", arr2,  "\nShape: ", arr2.shape)


# In[ ]:


## make change in one of the arrays, the change is reflected in both
arr2[1][1] = 99
print("\nOriginal Array: \n", arr1)
print("\nNew Array: \n", arr2)


# **Example 2:** Swapping axes of a 3-D array

# In[ ]:


arr1 = np.arange(8).reshape(2,2,2) 
print("Original Array: \n", arr1, "\nShape: ", arr1.shape)


# In[ ]:


#Reshape array using swapaxes() method
arr2 = np.swapaxes(arr1,1, 2)
print("\nNew array: \n", arr2,  "\nShape: ", arr2.shape)


# ### f. The `ndarray.flatten()` Method
# - The `ndarry.flatten()` method is used to flatten a Multi-Dimensional array/matrix to one dimension. 
# ```
# ndarray.flatten(order= 'C')
# ```
#    - Default order is 'C’, means to flatten in row-major order. 
#    - You can pass ‘F’ (FORTRAN) means to flatten in column-major.
# - Returns a copy of the array, flattened to one dimension.

# In[27]:


arr1 = np.arange(12).reshape(4,3) 
print("Original Array: \n", arr1, "\nDimensions: ", arr1.ndim)


# In[28]:


# flatten the array in row-major order
arr2 = arr1.flatten(order = 'C')
print("\nFlattened array in row major order \n", arr2, "\nDimensions: ", arr2.ndim)

# flatten the array in column-major order
arr3 = arr1.flatten(order = 'F')
print("\nFlattened array in cloumn major order \n", arr3, "\nDimensions: ", arr3.ndim)


# In[ ]:





# ## 3. Sorting Arrays using `np.sort()` Method
# - The `np.sort()` method returns a sorted copy of an array.
# - If axis is not specified, values can be of any shape and will be flattened before use
# ```
# np.sort(arr1, axis=-1, kind=None)
# ```
#     - `arr` : Array to be sorted.
#     - `axis` : Axis along which we need array to be started. The default is -1, which sorts along the last axis. 0 stands for sorting along first axis. If metioned None, the array is flattened before sorting.
#     - `kind` : default is 'quicksort', others can be 'mergesort', 'heapsort'

# ### a. Sorting a 1-D Array

# In[35]:


import numpy as np
arr1 = np.random.randint(low = 1, high = 100, size = 5)
print("arr1 = ", arr1)


# In[ ]:


arr2 = np.sort(arr1)
print("arr2 = ", arr2)


# ### b. Sorting a 2-D Array

# **Example 1:** Sorting a 2-D array with `axis=None`, array is flattened before sorting

# In[29]:


arr1 = np.random.randint(low = 1, high = 100, size = (3,3))
print("arr1: \n", arr1)


# In[30]:


arr2 = np.sort(arr1, axis = None)        
print ("\nSorting along axis=None: \n", arr2)


# **Example 2:** Sorting a 2-D array with `axis=0`, vertical axis, top to bottom

# In[31]:


arr1 = np.random.randint(low = 1, high = 10, size = (3,3))
print("arr1 = \n", arr1)


# In[32]:


arr2 = np.sort(arr1, axis = 0)        
print ("\nSorting along axis=0: \n", arr2)      


# **Example 3:** Sorting a 2-D array with `axis=1`, horizontal axis, left to right

# In[33]:


arr1 = np.random.randint(low = 1, high = 10, size = (3,3))
print("arr1 = \n", arr1)


# In[34]:


arr2 = np.sort(arr1, axis = 1)        
print ("\nSorting along axis=1: \n", arr2) 


# ## 4. Iterating numPy Arrays
# - Iterating over `ndarrays` is very similar to iterating over regular python arrays. 
# - Remember, iterating over multidimensional arrays is done with respect to the first axis.

# **Example 1:** Iterating over 1-D numPy array

# In[ ]:


arr1 = np.arange(12)
arr1


# In[ ]:


for value in arr1:
    print(value, end=' ')


# In[ ]:





# **Example 2:** Iterating over 2-D numPy array is done w.r.t first axis, i.e., zero axis (column wise). In simple words in the first iteration you will get the first row, in second iteration you will get the 2nd row and so on...

# In[ ]:


arr1 = np.arange(12).reshape(4, 3)
print("arr1: \n",arr1)


# In[ ]:


for zero_axis in arr1:
    print("Iteration:")
    print(zero_axis)


# **Example 3:** Iterating over 2-D numPy array

# In[ ]:


arr1 = np.arange(8).reshape(2, 4)
print("arr1: \n",arr1)


# In[ ]:


for zero_axis in arr1:
    print("Iteration:")
    print(zero_axis)


# In[ ]:





# **Example 4:** Iterating over 3-D numPy array is done w.r.t first axis, i.e., zero axis (level wise). In simple words in the first iteration you will get the first row, in second iteration you will get the 2nd row and so on...

# In[ ]:


arr1 = np.arange(24).reshape(2, 3, 4)
print("arr1: \n",arr1)


# In[ ]:


for zero_axis in arr1:
    print("Iteration:")
    print(zero_axis)


# **Example 5:** If you want to iterate on *all* elements in the `ndarray`, simply iterate over the `flat` attribute:

# In[ ]:


arr1 = np.arange(12).reshape(3, 4)
print("arr1: \n",arr1)


# In[ ]:


for i in arr1.flat:
    print(i, end=' ')


# In[ ]: