#!/usr/bin/env python
# coding: utf-8
# # Riskfolio-Lib Tutorial:
#
#
#

#
 #
#
#
__[Financionerioncios](https://financioneroncios.wordpress.com)__
#
__[Orenji](https://www.linkedin.com/company/orenj-i)__
#
__[Riskfolio-Lib](https://riskfolio-lib.readthedocs.io/en/latest/)__
#
__[Dany Cajas](https://www.linkedin.com/in/dany-cajas/)__
#
# ## Tutorial 13: Riskfolio-Lib and Xlwings
#
# ## 1. Downloading the data:
# In[ ]:
import numpy as np
import pandas as pd
import yfinance as yf
import warnings
warnings.filterwarnings("ignore")
pd.options.display.float_format = '{:.4%}'.format
# Date range
start = '2016-01-01'
end = '2019-12-30'
# Tickers of assets
assets = ['JCI', 'TGT', 'CMCSA', 'CPB', 'MO', 'APA', 'MMC', 'JPM',
'ZION', 'PSA', 'BAX', 'BMY', 'LUV', 'PCAR', 'TXT', 'TMO',
'DE', 'MSFT', 'HPQ', 'SEE', 'VZ', 'CNP', 'NI', 'T', 'BA']
assets.sort()
# Downloading data
data = yf.download(assets, start = start, end = end, auto_adjust=False)
data = data.loc[:,('Adj Close', slice(None))]
data.columns = assets
# In[2]:
# Calculating returns
Y = data[assets].pct_change().dropna()
display(Y.head())
# ## 2. Estimating Mean Variance Portfolios
#
# ### 2.1 Calculating the portfolio that maximizes Sharpe ratio.
# In[3]:
import riskfolio as rp
# Building the portfolio object
port = rp.Portfolio(returns=Y)
# Calculating optimal portfolio
# Select method and estimate input parameters:
method_mu='hist' # Method to estimate expected returns based on historical data.
method_cov='hist' # Method to estimate covariance matrix based on historical data.
port.assets_stats(method_mu=method_mu, method_cov=method_cov)
# Estimate optimal portfolio:
model='Classic' # Could be Classic (historical), BL (Black Litterman) or FM (Factor Model)
rm = 'MV' # Risk measure used, this time will be variance
obj = 'Sharpe' # Objective function, could be MinRisk, MaxRet, Utility or Sharpe
hist = True # Use historical scenarios for risk measures that depend on scenarios
rf = 0 # Risk free rate
l = 0 # Risk aversion factor, only useful when obj is 'Utility'
w = port.optimization(model=model, rm=rm, obj=obj, rf=rf, l=l, hist=hist)
display(w.T)
# ### 2.2 Plotting portfolio composition
# In[4]:
import matplotlib.pyplot as plt
# Plotting the composition of the portfolio
fig_1, ax_1 = plt.subplots(figsize=(10,6))
ax_1 = rp.plot_pie(w=w, title='Sharpe Mean Variance', others=0.05, nrow=25, cmap = "tab20",
height=6, width=10, ax=ax_1)
# ### 2.3 Calculate efficient frontier
# In[5]:
points = 50 # Number of points of the frontier
frontier = port.efficient_frontier(model=model, rm=rm, points=points, rf=rf, hist=hist)
display(frontier.T.head())
# In[6]:
# Plotting the efficient frontier
label = 'Max Risk Adjusted Return Portfolio' # Title of point
mu = port.mu # Expected returns
cov = port.cov # Covariance matrix
returns = port.returns # Returns of the assets
fig_2, ax_2 = plt.subplots(figsize=(10,6))
rp.plot_frontier(w_frontier=frontier, mu=mu, cov=cov, returns=returns, rm=rm,
rf=rf, alpha=0.01, cmap='viridis', w=w, label=label,
marker='*', s=16, c='r', height=6, width=10, ax=ax_2)
# In[7]:
# Plotting efficient frontier composition
fig_3, ax_3 = plt.subplots(figsize=(10,6))
rp.plot_frontier_area(w_frontier=frontier, cmap="tab20", height=6, width=10, ax=ax_3)
# ## 3. Combining Riskfolio-Lib and Xlwings
#
# ### 3.1 Creating an Empty Excel Workbook
# In[8]:
import xlwings as xw
# Creating an empty Excel Workbook
wb = xw.Book()
sheet1 = wb.sheets[0]
sheet1.name = 'Charts'
sheet2 = wb.sheets.add('Frontier')
sheet3 = wb.sheets.add('Optimal Weights')
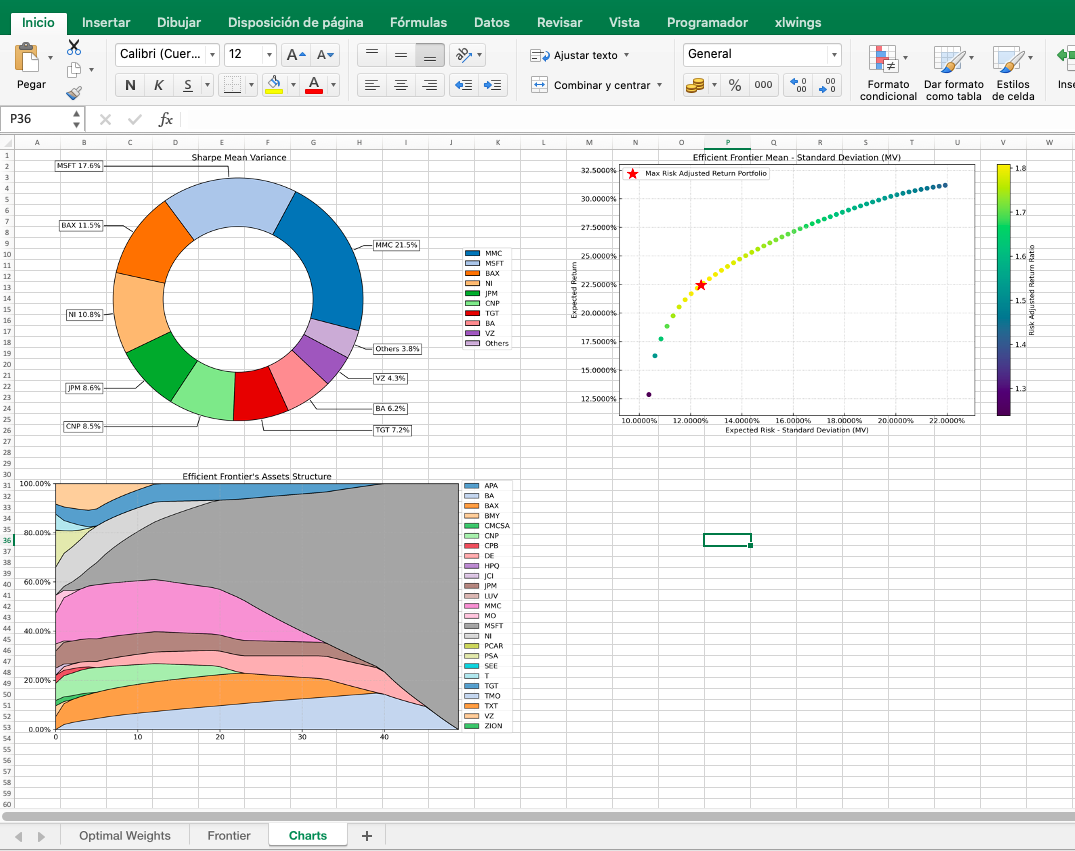
# ### 3.2 Adding Pictures to Sheet 1
# In[9]:
sheet1.pictures.add(fig_1, name = "Weights",
update = True,
top = sheet1.range("A1").top,
left = sheet1.range("A1").left)
sheet1.pictures.add(fig_2, name = "Frontier",
update = True,
top = sheet1.range("M1").top,
left = sheet1.range("M1").left)
sheet1.pictures.add(fig_3, name = "Composition",
update = True,
top = sheet1.range("A30").top,
left = sheet1.range("A30").left)
#  # ### 3.2 Adding Data to Sheet 2 and Sheet 3
# In[10]:
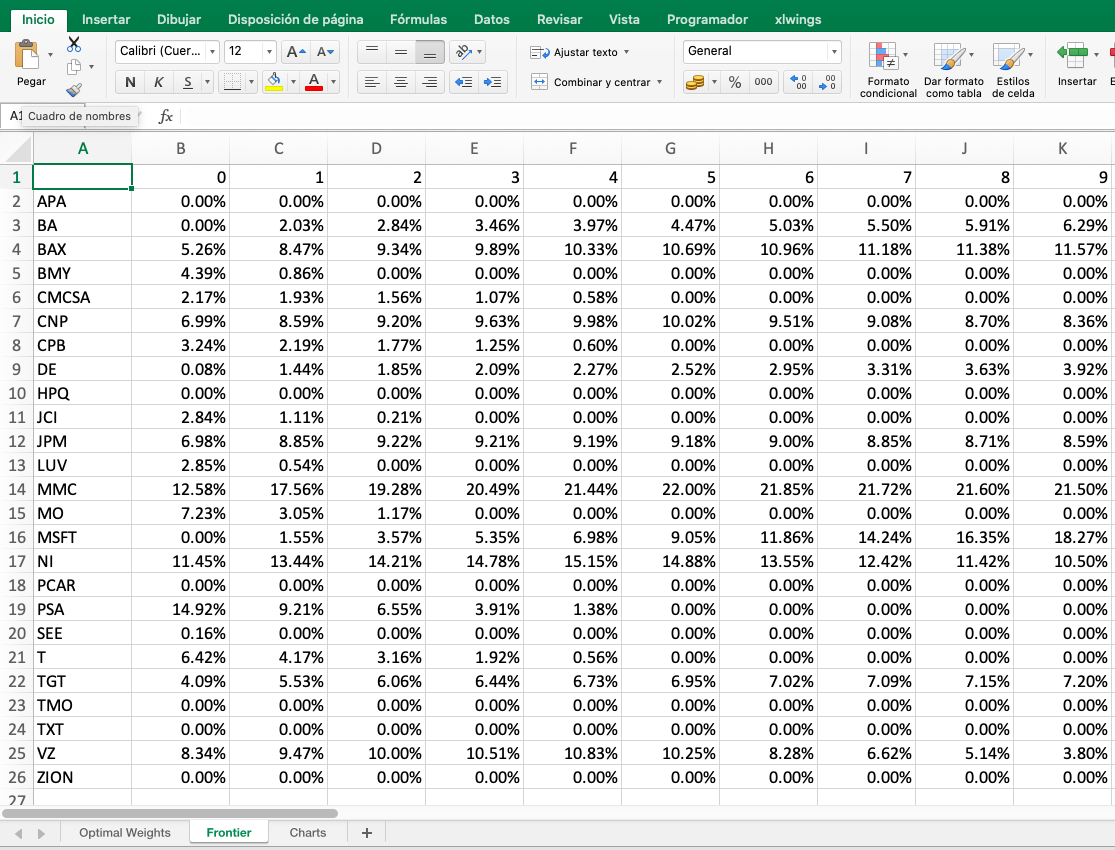
# Writing the weights of the frontier in the Excel Workbook
sheet2.range('A1').value = frontier.applymap('{:.6%}'.format)
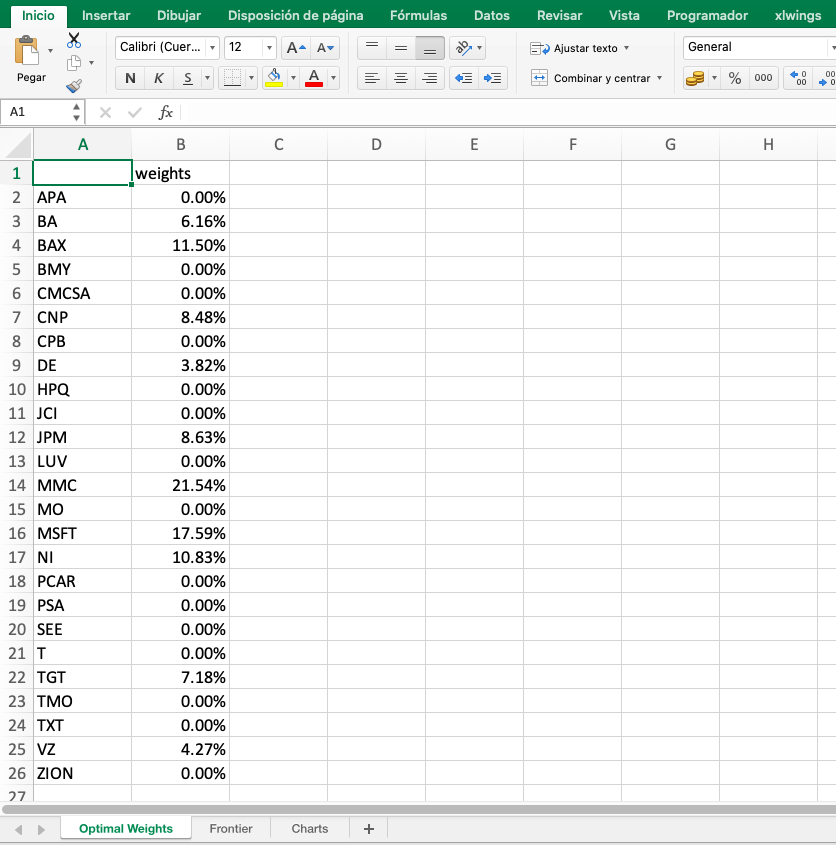
# Writing the optimal weights in the Excel Workbook
sheet3.range('A1').value = w.applymap('{:.6%}'.format)
#
# ### 3.2 Adding Data to Sheet 2 and Sheet 3
# In[10]:
# Writing the weights of the frontier in the Excel Workbook
sheet2.range('A1').value = frontier.applymap('{:.6%}'.format)
# Writing the optimal weights in the Excel Workbook
sheet3.range('A1').value = w.applymap('{:.6%}'.format)
#  #
# 
 # ### 3.2 Adding Data to Sheet 2 and Sheet 3
# In[10]:
# Writing the weights of the frontier in the Excel Workbook
sheet2.range('A1').value = frontier.applymap('{:.6%}'.format)
# Writing the optimal weights in the Excel Workbook
sheet3.range('A1').value = w.applymap('{:.6%}'.format)
#
# ### 3.2 Adding Data to Sheet 2 and Sheet 3
# In[10]:
# Writing the weights of the frontier in the Excel Workbook
sheet2.range('A1').value = frontier.applymap('{:.6%}'.format)
# Writing the optimal weights in the Excel Workbook
sheet3.range('A1').value = w.applymap('{:.6%}'.format)
#  #
# 