#!/usr/bin/env python
# coding: utf-8

# # "Implement Markowitz Portfolio Optimization in Only 3 Lines of Code"
# > "Use fastquant to maximize the returns of your stock portfolio given its overall risk profile"
# 
# - toc: true
# - branch: master
# - badges: true
# - comments: true
# - author: Benjamin Cabalona, Jerome de Leon
# - categories: [portfolio, optimization]

# In[1]:


# uncomment to install in colab
# !pip3 install fastquant


# <a href="https://colab.research.google.com/github/enzoampil/fastquant/blob/master/examples/2020-06-20-basic_portfolio.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>

# # Some Basic Ideas
# 
#  **Stock or Share** is a unit of ownership in a company. When you invest in the stock market, (stock market is basically a place for buying or selling stocks) there are 2 main ways of earning:
#  
# - **Dividend** - This is an amount paid to you by a company for your investment. 
# - **Stock Trading** - The profit that you make for buying/selling stocks.
# - **Portfolio** - A combination of assets of an individual / investor.
# 
# Fundamentally, you can earn money by buying some stocks, in the hope that it's price will increase in the future. 
# 
# There are actually clever ways on how to earn even if you predict that a stock price will decline, but that's outside the scope of this lecture.
# 
# So in this lecture, we'll oversimplify and what we want is to **buy a stock cheap, and sell it when its price has increased** because that way we will make a profit. Otherwise we will incur a loss, if we decided to sell a stock at a cheaper price.

# 
# # Modern Portfolio Theory (Markowitz Model)
# 
# As mentioned above, investing in the stock market can result in either profit or loss. 
# 
# In a nutshell, Modern Portfolio Theory is a way of maximizing return for a given risk. We will define what *return* and *risk* means shortly.
# 
# Let's understand this by using an example.
# 
# Suppose you wanted to invest in the stock market. After completing your research, you decided to invest in the following companies:
# 
# - MEG
# - MAXS
# - JFC
# - ALI
# 
# We will download the data for this using a python library called fastquant. It was actually developed by a fellow Filipino Data Scientist. It aims to democratize data-driven investments for everyone.
# 
# 
# **NOTE** The model we'll be using relies on the assumption that returns are normally distributed. Therefore, it helps if we have large number of data points.

# In[2]:


import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings

import scipy.optimize as optimization
from fastquant import get_stock_data
warnings.filterwarnings('ignore')
get_ipython().run_line_magic('matplotlib', 'inline')


# In[3]:


stocks = ['MEG', 'MAXS', 'JFC', 'ALI']
datas = []
for i in stocks:
    df = get_stock_data(i, "2017-01-01", "2020-01-01")
    df = df.reset_index()
    df.columns = ['DATE',i]
    df = df[['DATE',i]]
    datas.append(df)
datas1 = pd.merge(datas[0],datas[1],on=['DATE'])
datas2 = pd.merge(datas[2],datas[3],on=['DATE'])
data = pd.merge(datas1,datas2,on=['DATE'])
data.index = data['DATE']
data.drop('DATE',axis=1,inplace=True)


# The table below shows the first 5 entries in our dataset. The values here are *closing prices*. A *closing price* is a price of a stock at the end of a given trading day.

# In[4]:


data.head()


# Now, let's ask ourselves. Why don't we invest in a single company, instead of investing in multiple companies?
# 
# Modern Portfolio Theory tells us that we can *minimize* our loss thru diversification. Let's understand this with an example.
# 
# Suppose you decided to invest on January 2017. For illustraton purposes, let's consider the period January 2017 - May 2018.
# 
# - Case 1: You invested solely on MAXS
# - Case 2: You decided to invest 50% to MAXS and the other 50% to JFC
# 
# If you decided to go with case 1, it would be clear that you could immediately lose some money (as the chart shows a decreasing trend). If you instead decided to go with Case 2, your loss could have been mitigated since the price for JFC is increasing during that period.
# 
# Of course you could argue that "why not invest all of my money in JFC", well my counter argument to that would be, when JFC is experiencing a decline in it's price, there would be some other company that's actually experiencing an increase in it's price.
# 
# ## Key Takeaway 
# 
# - Invest in multiple stocks as much as possible, to minimize your loss. (Technically uncorrelated or negatively correlated)

# In[5]:


data['MAXS'].plot(figsize=(12,5),legend=True)


# In[6]:


data['JFC'].plot(figsize=(12,5),legend=True,color='r')


# Now, let's define what a return is. Intuitively, we can define return as :
# 
# *The stock price today minus the stock price yesterday. Divide the difference by the stock price yesterday*
# 
# More formally,
# 
# The *return* $R_{t,t+1}$ from time $t$ to time ${t+1}$ is given by:
# 
# $$ R_{t,t+1} = \frac{P_{t+1}-P_{t}}{P_{t}} $$
# 
# where $P_i$ is the price of the stock for a given time point.

# In[7]:


returns = data.pct_change()
returns


# The mean of the returns is called the **Expected Return**. 
# 
# Similarly, the **Risk or Volatility** is the standard deviation of the returns.
# 
# (This is different from the expected return and volatility of a portfolio, this is for a single stock)

# In[8]:


returns.mean()


# In[9]:


returns.std()


# We'll only plot MAXS and MEG to emphasize that the return for MEG is more volatile.

# In[10]:


returns[['MAXS','MEG']].plot(figsize=(12,5))


# ## Expected Return and Risk of a Portfolio
# 
# Suppose your portfolio consists of returns $R_1, R_2, R_3, ... ,R_n$. Then, the expected return of a portfolio is given by:
# 
# $E(R) = w_1E(R_1) + w_2E(R_2) + w_3E(R_3) + ... + w_nE(R_n) $
# 
# where $w_i$ is the $i$th component of an $n-dimensional$  vector, and $\Sigma w_i = 1.$

# In[11]:


weights = np.random.random(len(stocks))
weights /= np.sum(weights)
weights


# In[12]:


returns.mean()


# In[13]:


def calculate_portfolio_return(returns, weights):
    portfolio_return = np.sum(returns.mean()*weights)*252
    print("Expected Portfolio Return:", portfolio_return)


# In[14]:


calculate_portfolio_return(returns,weights)


# If you had a course in Probability, you might recall that expectation of a random variable is linear while the variance is not. That's the same argument why the formula for the variance of a portfolio is quite more complicated.
# 
# $Var(R) = \bf{w^{T}}\Sigma \textbf{w}$
# 
# where $\Sigma$ is the covariance matrix of $R_i$

# In[15]:


returns.cov()


# In[16]:


np.sqrt(returns.cov())


# In[17]:


returns.std()


# In[18]:


def calculate_portfolio_risk(returns, weights):
    portfolio_variance = np.sqrt(np.dot(weights.T, np.dot(returns.cov()*252,weights)))
    print("Expected Risk:", portfolio_variance)


# In[19]:


calculate_portfolio_risk(returns,weights)


# ## Sharpe Ratio
# 
# 
# Remember, what we want is to find the best possible weight vector $\bf{w}$ that would give us the best possible return, with a minimal risk. Therefore, we will introduce a new metric called the *sharpe ratio*. It's simply equal to 
# 
# $$S.R. = \frac{E(R) - R_f}{\sqrt{Var(R)}}$$
# 
# where $R_f$ is the *risk free return*. Since we're only limiting ourselves to risky assets (stocks) therefore, the formula becomes
# 
# $$S.R. = \frac{E(R) - 0}{\sqrt{Var(R)}} = \frac{E(R)}{\sqrt{Var(R)}}$$

# In[20]:


def generate_portfolios(weights, returns):

    preturns = []
    pvariances = []


    for i in range(10000):
        weights = np.random.random(len(stocks))
        weights/=np.sum(weights)
        preturns.append(np.sum(returns.mean()*weights)*252)
        pvariances.append(np.sqrt(np.dot(weights.T,np.dot(returns.cov()*252,weights))))

    preturns = np.array(preturns)
    pvariances = np.array(pvariances)
    return preturns,pvariances

def plot_portfolios(returns, variances):
    plt.figure(figsize=(10,6))
    plt.scatter(variances,returns,c=returns/variances,marker='o')
    plt.grid(True)
    plt.xlabel('Expected Volatility')
    plt.ylabel('Expected Return')
    plt.colorbar(label='Sharpe Ratio')
    plt.show()


# In[21]:


preturns, pvariances = generate_portfolios(weights,returns)


# ## Monte - Carlo Simulation
# 
# Here, we simulated 10,000 possible weight allocations, and computed their respective expected return, risk and sharpe ratio.

# In[22]:


plot_portfolios(preturns, pvariances)


# # Finding and plotting the Optimal Weights (the hard way)
# 
# At a high level, we would want to run an optimization algorithm that would 
# 
# 
# $$maximize\  \frac{E(R)-R_f}{\sqrt{Var(R)}}$$
# 
# $$s.t. \forall w_i, w_i\geq0\ and\ \Sigma w_i=1$$
# 
# Full details of the mathematics behind this can be found on resources.

# In[23]:


def statistics(weights, returns):
    portfolio_return=np.sum(returns.mean()*weights)*252
    portfolio_volatility=np.sqrt(np.dot(weights.T,np.dot(returns.cov()*252,weights)))
    return np.array([portfolio_return,portfolio_volatility,portfolio_return/portfolio_volatility])


def min_func_sharpe(weights,returns):
    return -statistics(weights,returns)[2] 


def optimize_portfolio(weights,returns):
    constraints = ({'type':'eq','fun': lambda x: np.sum(x)-1}) 
    bounds = tuple((0,1) for x in range(len(stocks))) 
    optimum=optimization.minimize(fun=min_func_sharpe,x0=weights,args=returns,method='SLSQP',bounds=bounds,constraints=constraints) 
    return optimum


def print_optimal_portfolio(optimum, returns):
    print("Optimal weights:", optimum['x'].round(3))
    print("Expected return, volatility and Sharpe ratio:", statistics(optimum['x'].round(3),returns))

def show_optimal_portfolio(optimum, returns, preturns, pvariances):
    plt.figure(figsize=(10,6))
    plt.scatter(pvariances,preturns,c=preturns/pvariances,marker='o')
    plt.grid(True)
    plt.xlabel('Expected Volatility')
    plt.ylabel('Expected Return')
    plt.colorbar(label='Sharpe Ratio')
    plt.plot(statistics(optimum['x'],returns)[1],statistics(optimum['x'],returns)[0],'g*',markersize=20.0)
    plt.show()


# In[24]:


optimum=optimize_portfolio(weights,returns)
print_optimal_portfolio(optimum, returns)
show_optimal_portfolio(optimum, returns, preturns, pvariances)


# # Finding and plotting the Optimal Weights (the fastquant way)
# 
# Since our goal is to promote data driven investments by making quantitative analysis in finance accessible to everyone, the markowitz model is also implemented in fastquant. All it takes is a few lines of code as shown below.

# In[25]:


from fastquant import Portfolio


# In[26]:


stock_list = ['MEG', 'MAXS', 'JFC', 'ALI']
p = Portfolio(stock_list,"2017-01-01", "2020-01-01")

axs = p.data.plot(subplots=True, figsize=(15,10))
fig = p.plot_portfolio(N=1000)


# # Bonus Section : Interactive Charts
# 
# This section is expected to **NOT** render in github, but does in fastpages.
# 
# It is expected to look like the image below, and in addition, the tooltip is interactive.
# 
#  <img src="chart.png"  width="700" height="700"> 
# 
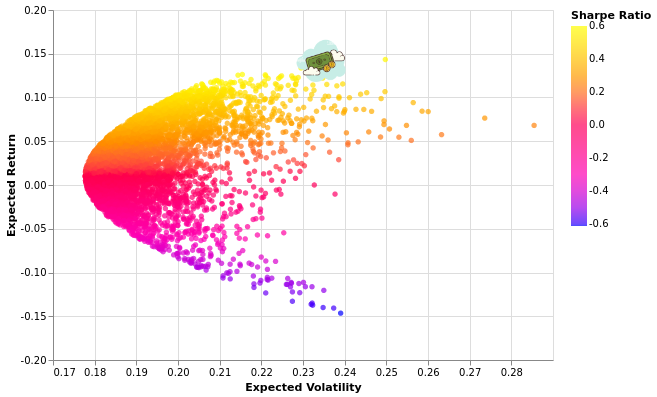# Refer to this link https://altair-viz.github.io/getting_started/installation.html for altair's installation, but most likely
# 
# ```python
# !pip3 install altair
# ```
# 
# should do the trick.

# In[27]:


import altair as alt
alt.renderers.set_embed_options(actions=False)


# In[28]:


weights = pd.DataFrame(optimum['x'].round(2),columns=['weights'])
weights['Symbols'] = stocks


# In[29]:


returns,variances = p.generate_portfolios(N=5000)
portfolios = pd.DataFrame()
portfolios['Expected Return'] = returns
portfolios['Expected Volatility'] = variances
portfolios['Sharpe Ratio'] = portfolios['Expected Return'] / portfolios['Expected Volatility']
minimumX = portfolios['Expected Volatility'].min()
maximumX = portfolios['Expected Volatility'].max()
minimumY = portfolios['Expected Return'].min()
maximumY = portfolios['Expected Return'].max()


optimum = p.calculate_statistics(p.optimum_weights)
optimal = pd.DataFrame()
optimal['Expected Return'] = [optimum[0]]
optimal['Expected Volatility'] = [optimum[1]]
optimal['Sharpe Ratio'] = [optimum[2]]
optimal['img'] = "https://img.icons8.com/clouds/100/000000/us-dollar--v1.png"


# In[30]:


# uncomment if N > 5000
# alt.data_transformers.enable('json')


# In[31]:


chart = alt.Chart(portfolios).mark_circle().encode(
    x = alt.X('Expected Volatility',scale=alt.Scale(domain=[minimumX,maximumX])),
    y = alt.X('Expected Return',scale=alt.Scale(domain=[minimumY,maximumY])),
    color = alt.Color('Sharpe Ratio',scale=alt.Scale(range=['blue','yellow'])),
    tooltip = ['Sharpe Ratio']

).properties(height=350,width=500)

optimal_chart = alt.Chart(optimal).mark_image(height=60,width=60).encode(
    x = alt.X('Expected Volatility',scale=alt.Scale(domain=[minimumX,maximumX])),
    y = alt.X('Expected Return',scale=alt.Scale(domain=[minimumY,maximumY])),
    color = alt.Color('Sharpe Ratio',scale=alt.Scale(range=['blue','yellow'])),
    tooltip = ['Sharpe Ratio'],
    url = 'img'

).properties(height=350,width=500)

visualization = chart+optimal_chart

visualization


# Resources:
# 
# - Financial Mathematics
#     - https://www.springer.com/gp/book/9780857290816
# - General Investing
#     - https://www.ig.com/en/learn-to-trade/ig-academy