#!/usr/bin/env python
# coding: utf-8

# # 10. Implementing QR Factorization

# We used QR factorization in computing eigenvalues and to compute least squares regression. It is an important building block in numerical linear algebra.
# 
# "One algorithm in numerical linear algebra is more important than all the others: QR factorization." --Trefethen, page 48
# 
# Recall that for any matrix $A$, $A = QR$ where $Q$ is orthogonal and $R$ is upper-triangular.

# **Reminder**: The *QR algorithm*, which we looked at in the last lesson, uses the *QR decomposition*, but don't confuse the two.

# ### In Numpy ###

# In[5]:


import numpy as np

np.set_printoptions(suppress=True, precision=4)


# In[6]:


n = 5
A = np.random.rand(n,n)
npQ, npR = np.linalg.qr(A)


# Check that Q is orthogonal:

# In[7]:


np.allclose(np.eye(n), npQ @ npQ.T), np.allclose(np.eye(n), npQ.T @ npQ)


# Check that R is triangular

# In[8]:


npR


# ### Linear Algebra Review: Projections

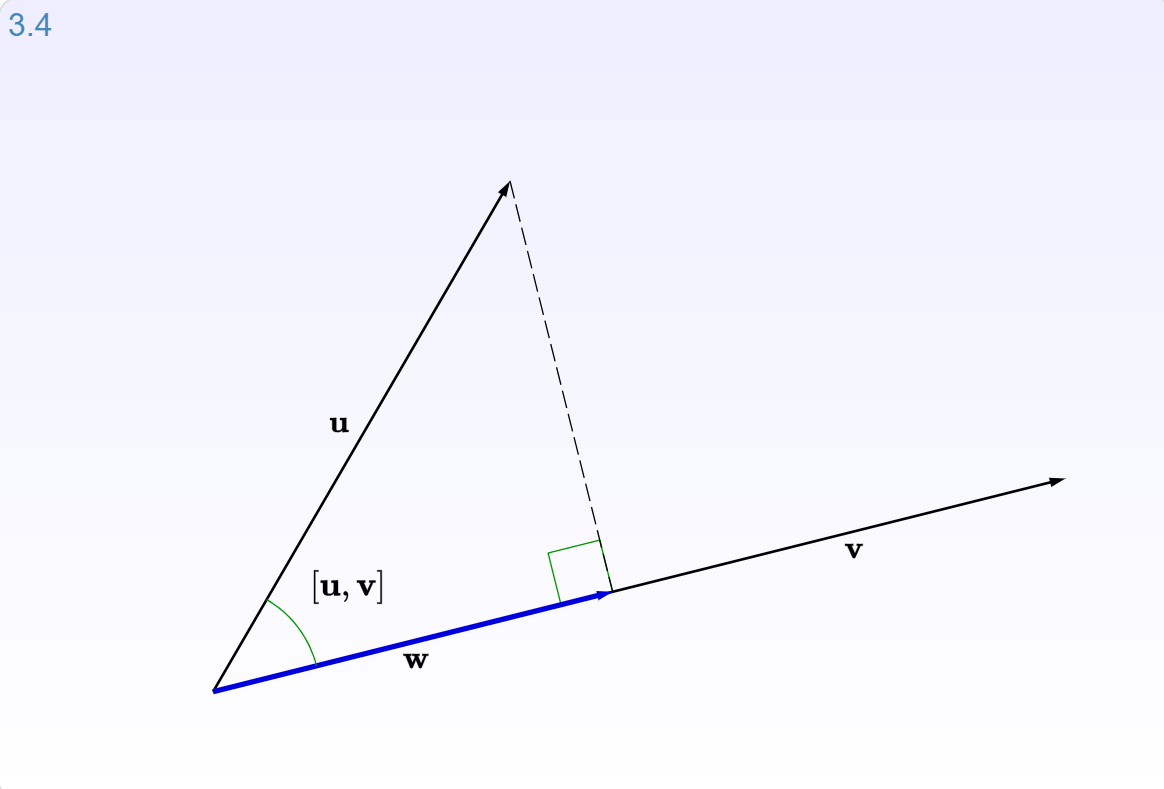
# When vector $\mathbf{b}$ is projected onto a line $\mathbf{a}$, its projection $\mathbf{p}$ is the part of $\mathbf{b}$ along that line $\mathbf{a}$.
# 
# Let's look at interactive graphic (3.4) for [section 3.2.2: Projections](http://immersivemath.com/ila/ch03_dotproduct/ch03.html) of the [Immersive Linear Algebra online book](http://immersivemath.com/ila/index.html).
# 
# <img src="images/projection_line.png" alt="projection" style="width: 70%"/>
# (source: [Immersive Math](http://immersivemath.com/ila/ch03_dotproduct/ch03.html))
# 
# And here is what it looks like to project a vector onto a plane:
# 
# <img src="images/projection.png" alt="projection" style="width: 70%"/>
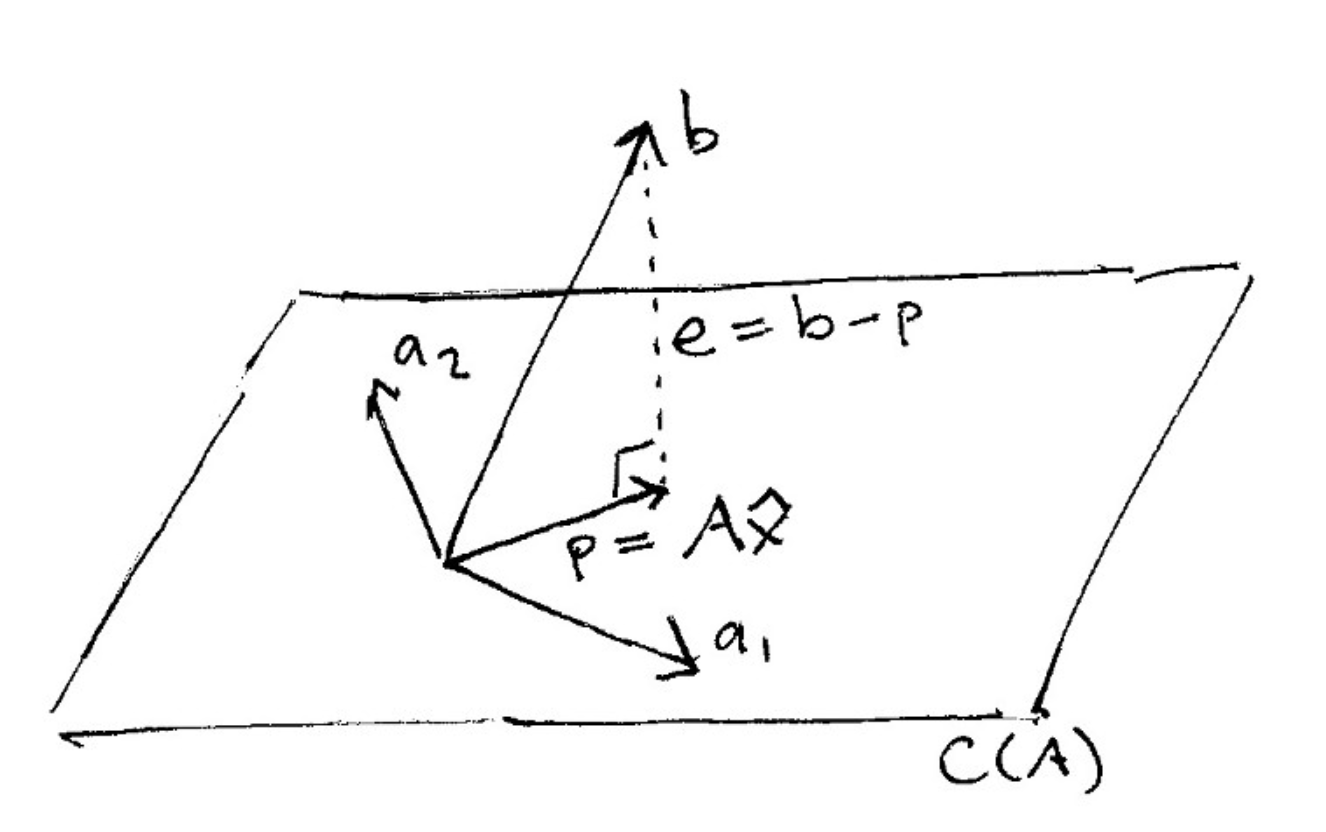# (source: [The Linear Algebra View of Least-Squares Regression](https://medium.com/@andrew.chamberlain/the-linear-algebra-view-of-least-squares-regression-f67044b7f39b))
# 
# When vector $\mathbf{b}$ is projected onto a line $\mathbf{a}$, its projection $\mathbf{p}$ is the part of $\mathbf{b}$ along that line $\mathbf{a}$.  So $\mathbf{p}$ is some multiple of $\mathbf{a}$. Let $\mathbf{p} = \hat{x}\mathbf{a}$ where $\hat{x}$ is a scalar.

# #### Orthogonality

# **The key to projection is orthogonality:** The line *from* $\mathbf{b}$ to $\mathbf{p}$ (which can be written $\mathbf{b} - \hat{x}\mathbf{a}$) is perpendicular to $\mathbf{a}$.
# 
# This means that $$ \mathbf{a} \cdot (\mathbf{b} -  \hat{x}\mathbf{a}) = 0 $$
# 
# and so $$\hat{x} = \frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{a} \cdot \mathbf{a}} $$

# ## Gram-Schmidt ##

# ### Classical Gram-Schmidt (unstable) ###

# For each $j$, calculate a single projection $$v_j = P_ja_j$$ where $P_j$ projects onto the space orthogonal to the span of $q_1,\ldots,q_{j-1}$.

# In[10]:


def cgs(A):
    m, n = A.shape
    Q = np.zeros([m,n], dtype=np.float64)
    R = np.zeros([n,n], dtype=np.float64)
    for j in range(n):
        v = A[:,j]
        for i in range(j):
            R[i,j] = np.dot(Q[:,i], A[:,j])
            v = v - (R[i,j] * Q[:,i])
        R[j,j] = np.linalg.norm(v)
        Q[:, j] = v / R[j,j]
    return Q, R


# In[190]:


Q, R = cgs(A)


# In[191]:


np.allclose(A, Q @ R)


# Check if Q is unitary:

# In[109]:


np.allclose(np.eye(len(Q)), Q.dot(Q.T))


# In[115]:


np.allclose(npQ, -Q)


# In[192]:


R


# Gram-Schmidt should remind you a bit of the Arnoldi Iteration (used to transform a matrix to Hessenberg form) since it is also a structured orthogonalization.

# ### Modified Gram-Schmidt ###

# Classical (unstable) Gram-Schmidt: for each $j$, calculate a single projection $$v_j = P_ja_j$$ where $P_j$ projects onto the space orthogonal to the span of $q_1,\ldots,q_{j-1}$.
# 
# Modified Gram-Schmidt: for each $j$, calculate $j-1$ projections $$P_j = P_{\perp q_{j-1}\cdots\perp q_{2}\perp q_{1}}$$

# In[30]:


import numpy as np
n = 3
A = np.random.rand(n,n).astype(np.float64)


# In[10]:


def cgs(A):
    m, n = A.shape
    Q = np.zeros([m,n], dtype=np.float64)
    R = np.zeros([n,n], dtype=np.float64)
    for j in range(n):
        v = A[:,j]
        for i in range(j):
            R[i,j] = np.dot(Q[:,i], A[:,j])
            v = v - (R[i,j] * Q[:,i])
        R[j,j] = np.linalg.norm(v)
        Q[:, j] = v / R[j,j]
    return Q, R


# In[33]:


def mgs(A):
    V = A.copy()
    m, n = A.shape
    Q = np.zeros([m,n], dtype=np.float64)
    R = np.zeros([n,n], dtype=np.float64)
    for i in range(n):
        R[i,i] = np.linalg.norm(V[:,i])
        Q[:,i] = V[:,i] / R[i,i]
        for j in range(i, n):
            R[i,j] = np.dot(Q[:,i],V[:,j])
            V[:,j] = V[:,j] - R[i,j]*Q[:,i]
    return Q, R


# In[34]:


Q, R = mgs(A)


# In[35]:


np.allclose(np.eye(len(Q)), Q.dot(Q.T.conj()))


# In[36]:


np.allclose(A, np.matmul(Q,R))


# ## Householder

# ### Intro

# \begin{array}{ l | l | c }
# \hline
# Gram-Schmidt & Triangular\, Orthogonalization & A R_1 R_2 \cdots R_n = Q  \\
# Householder  & Orthogonal\, Triangularization & Q_n \cdots Q_2 Q_1 A = R  \\
# \hline
# \end{array}

# Householder reflections lead to a more nearly orthogonal matrix Q with rounding errors
# 
# Gram-Schmidt can be stopped part-way, leaving a reduced QR of 1st n columns of A

# ### Initialization

# In[113]:


import numpy as np
n = 4
A = np.random.rand(n,n).astype(np.float64)

Q = np.zeros([n,n], dtype=np.float64)
R = np.zeros([n,n], dtype=np.float64)


# In[114]:


A


# In[115]:


from scipy.linalg import block_diag


# In[116]:


np.set_printoptions(5)


# ### Algorithm

# I added more computations and more info than needed, since it's illustrative of how the algorithm works.  This version returns the *Householder Reflectors* as well.

# In[117]:


def householder_lots(A):
    m, n = A.shape
    R = np.copy(A)
    V = []
    Fs = []
    for k in range(n):
        v = np.copy(R[k:,k])
        v = np.reshape(v, (n-k, 1))
        v[0] += np.sign(v[0]) * np.linalg.norm(v)
        v /= np.linalg.norm(v)
        R[k:,k:] = R[k:,k:] - 2*np.matmul(v, np.matmul(v.T, R[k:,k:]))
        V.append(v)
        F = np.eye(n-k) - 2 * np.matmul(v, v.T)/np.matmul(v.T, v)
        Fs.append(F)
    return R, V, Fs


# Check that R is upper triangular:

# In[121]:


R


# As a check, we will calculate $Q^T$ and $R$ using the block matrices $F$.  The matrices $F$ are *the householder reflectors*.
# 
# Note that this is not a computationally efficient way of working with $Q$.  In most cases, you do not actually need $Q$.  For instance, if you are using QR to solve least squares, you just need $Q^*b$.
# 
# - See page 74 of Trefethen for techniques to implicitly calculate the product $Q^*b$ or $Qx$.
# - See [these lecture notes](http://www.cs.cornell.edu/~bindel/class/cs6210-f09/lec18.pdf) for a different implementation of Householder that calculates Q simultaneously as part of R. 

# In[175]:


QT = np.matmul(block_diag(np.eye(3), F[3]), 
               np.matmul(block_diag(np.eye(2), F[2]), 
                         np.matmul(block_diag(np.eye(1), F[1]), F[0])))


# In[178]:


F[1]


# In[177]:


block_diag(np.eye(1), F[1])


# In[193]:


block_diag(np.eye(2), F[2])


# In[194]:


block_diag(np.eye(3), F[3])


# In[176]:


np.matmul(block_diag(np.eye(1), F[1]), F[0])


# In[123]:


QT


# In[124]:


R2 = np.matmul(block_diag(np.eye(3), F[3]), 
               np.matmul(block_diag(np.eye(2), F[2]),
                         np.matmul(block_diag(np.eye(1), F[1]), 
                                   np.matmul(F[0], A))))


# In[125]:


np.allclose(A, np.matmul(np.transpose(QT), R2))


# In[126]:


np.allclose(R, R2)


# Here's a concise version of Householder (although I do create a new R, instead of overwriting A and computing it in place).

# In[179]:


def householder(A):
    m, n = A.shape
    R = np.copy(A)
    Q = np.eye(m)
    V = []
    for k in range(n):
        v = np.copy(R[k:,k])
        v = np.reshape(v, (n-k, 1))
        v[0] += np.sign(v[0]) * np.linalg.norm(v)
        v /= np.linalg.norm(v)
        R[k:,k:] = R[k:,k:] - 2 * v @ v.T @ R[k:,k:]
        V.append(v)
    return R, V


# In[157]:


RH, VH = householder(A)


# Check that R is diagonal:

# In[129]:


RH


# In[130]:


VH


# In[131]:


np.allclose(R, RH)


# In[132]:


def implicit_Qx(V,x):
    n = len(x)
    for k in range(n-1,-1,-1):
        x[k:n] -= 2*np.matmul(v[-k], np.matmul(v[-k], x[k:n]))


# In[133]:


A


# Both classical and modified Gram-Schmidt require $2mn^2$ flops.

# ### Gotchas

# Some things to be careful about:
# - when you've copied values vs. when you have two variables pointing to the same memory location
# - the difference between a vector of length n and a 1 x n matrix (np.matmul deals with them differently)

# ## Analogy

# |                              | $A = QR$     | $A = QHQ^*$ |
# |------------------------------|--------------|-------------|
# | orthogonal structuring       | Householder  | Householder |
# | structured orthogonalization | Gram-Schmidt | Arnoldi     |
# 
# **Gram-Schmidt and Arnoldi**: succession of triangular operations, can be stopped part way and first $n$ columns are correct
# 
# **Householder**: succession of orthogoal operations.  Leads to more nearly orthogonal A in presence of rounding errors.
# 
# Note that to compute a Hessenberg reduction $A = QHQ^*$, Householder reflectors are applied to two sides of A, rather than just one.

# # Examples

# The following examples are taken from Lecture 9 of Trefethen and Bau, although translated from MATLAB into Python

# ### Ex: Classical vs Modified Gram-Schmidt ###

# This example is experiment 2 from section 9 of Trefethen. We want to construct a square matrix A with random singular vectors and widely varying singular values spaced by factors of 2 between $2^{-1}$ and $2^{-(n+1)}$

# In[68]:


import matplotlib.pyplot as plt
from matplotlib import rcParams
get_ipython().run_line_magic('matplotlib', 'inline')


# In[183]:


n = 100
U, X = np.linalg.qr(np.random.randn(n,n))   # set U to a random orthogonal matrix
V, X = np.linalg.qr(np.random.randn(n,n))   # set V to a random orthogonal matrix
S = np.diag(np.power(2,np.arange(-1,-(n+1),-1), dtype=float))  # Set S to a diagonal matrix w/ exp 
                                                              # values between 2^-1 and 2^-(n+1)


# In[184]:


A = np.matmul(U,np.matmul(S,V))


# In[188]:


QC, RC = cgs(A)
QM, RM = mgs(A)


# In[189]:


plt.figure(figsize=(10,10))
plt.semilogy(np.diag(S), 'r.', basey=2, label="True Singular Values")
plt.semilogy(np.diag(RM), 'go', basey=2, label="Modified Gram-Shmidt")
plt.semilogy(np.diag(RC), 'bx', basey=2, label="Classic Gram-Shmidt")
plt.legend()
rcParams.update({'font.size': 18})


# In[94]:


type(A[0,0]), type(RC[0,0]), type(S[0,0])


# In[92]:


eps = np.finfo(np.float64).eps; eps


# In[93]:


np.log2(eps), np.log2(np.sqrt(eps))


# ### Ex: Numerical loss of orthogonality

# This example is experiment 3 from section 9 of Trefethen.

# In[197]:


A = np.array([[0.70000, 0.70711], [0.70001, 0.70711]])


# In[198]:


A


# Gram-Schmidt:

# In[96]:


Q1, R1 = mgs(A)


# Householder:

# In[105]:


R2, V, F = householder_lots(A)
Q2T = np.matmul(block_diag(np.eye(1), F[1]), F[0])


# Numpy's Householder:

# In[106]:


Q3, R3 = np.linalg.qr(A)


# Check that all the QR factorizations work:

# In[107]:


np.matmul(Q1, R1)


# In[108]:


np.matmul(Q2T.T, R2)


# In[109]:


np.matmul(Q3, R3)


# Check how close Q is to being perfectly orthonormal:

# In[110]:


np.linalg.norm(np.matmul(Q1.T, Q1) - np.eye(2))  # Modified Gram-Schmidt


# In[111]:


np.linalg.norm(np.matmul(Q2T.T, Q2T) - np.eye(2))  # Our implementation of Householder


# In[112]:


np.linalg.norm(np.matmul(Q3.T, Q3) - np.eye(2))  # Numpy (which uses Householder)


# GS (Q1) is less stable than Householder (Q2T, Q3)

# # End