#!/usr/bin/env python
# coding: utf-8

# ### Introduction 
# 
# Controlling what a generative model produces is still a significant challenge. Diffusion models have introduced an unprecedented level of control compared to earlier approaches, but the process is far from perfect. You might generate an image, attempt a minor change, and find that the entire scene shifts just because you slightly adjusted the prompt.
# 
# There has been considerable effort toward enabling more precise and user-friendly image editing methods that are more targeted and stable. In this post, I aim to tell the story of how these techniques have rapidly evolved over the last few years.
# 

# ### Contents
# 
# 1. [Prompt-to-Prompt Image Editing with Cross-Attention Control (ICLR 2023)](#prompt-to-prompt-image-editing-with-cross-attention-control-iclr-2023)
# 2. [InstructPix2Pix: Learning to Follow Image Editing Instructions (CVPR 2023)](#instructpix2pix-learning-to-follow-image-editing-instructions-cvpr-2023)
# 3. [Null-text Inversion for Editing Real Images using Guided Diffusion Models (CVPR 2023)](#null-text-inversion-for-editing-real-images-using-guided-diffusion-models-cvpr-2023)
# 

# ### Prompt-to-Prompt Image Editing with Cross-Attention Control (ICLR 2023)
# 
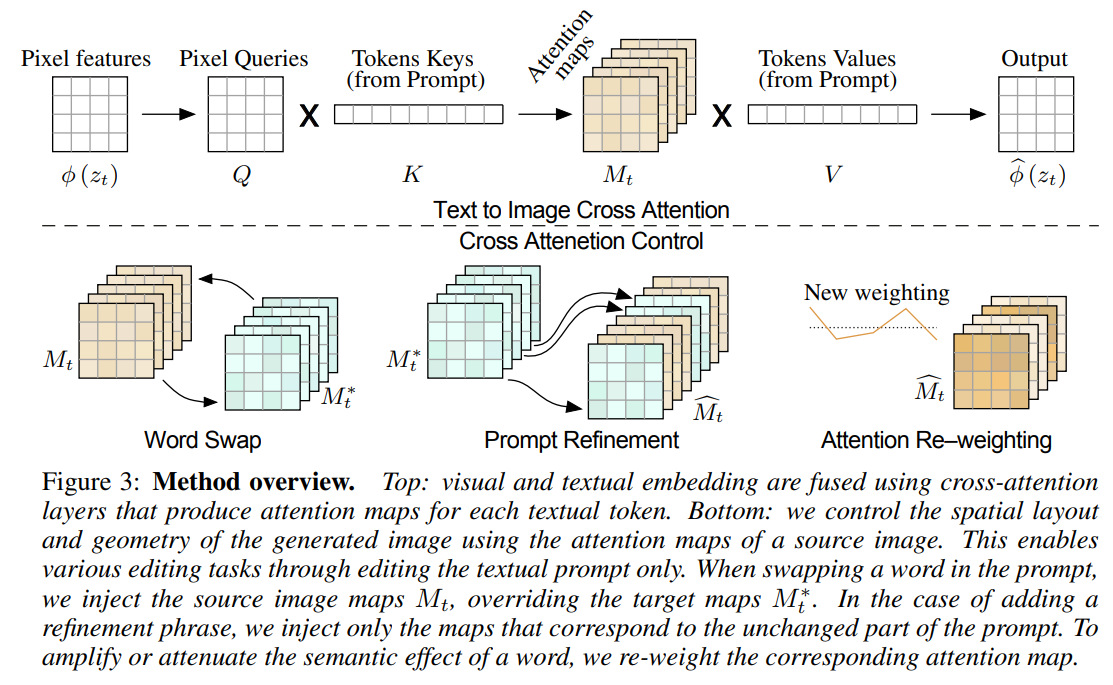
# It often happens that you generate an image but want to modify certain aspects without changing the entire scene. However, if you try to make that change by slightly adjusting the prompt in a text-to-image model (such as Stable Diffusion), you will likely end up with a completely different image.
# 
# The goal of this paper is to provide more control during image editing, allowing you to make targeted changes to specific parts of the generated image while keeping the rest intact. Here is an example from the paper:

# <div style="text-align: center;">
#   <img src="blog_pics/prompt2prompt_1.png" alt="" width="400">
# </div>
# 

# Recent methods in text-to-image generation often inject contextual information into the generated image using cross-attention. Typically, the text embeddings provide the keys and values (text → $k$, $v$), while the image features provide the queries (image → $q$).
# 
# The cross-attention mechanism can be written as:
# 
# $$
# \text{Attention}(q, k, v) = \text{softmax}\left( \frac{q k^\top}{\sqrt{d}} \right) v
# $$
# 
# Where:
# - $q \in \mathbb{R}^{N_q \times d}$: queries from image features
# - $k, v \in \mathbb{R}^{N_k \times d}$: keys and values from text embeddings
# - $d$: dimensionality of the embeddings
# - $N_q$: number of image query tokens (e.g., spatial positions in the image)
# - $N_k$: number of text tokens
# 
# This allows the model to attend to relevant parts of the text when updating each spatial location in the image. Following the notation from authors, I will refer to $\text{softmax}\left( \frac{q k^\top}{\sqrt{d}} \right)$ as attention map $M$.

# As we have seen, the attention map determines how the generated image responds to the input text. But why does changing just a single word in the prompt often result in a completely different image?
# 
# This is largely due to the stochastic nature of the denoising process in diffusion models. As the model gradually transforms noise into a coherent image, even small changes in the prompt can lead to significant change in the final output. Although the word embeddings for the unchanged parts of the prompt remain the same, the image-side queries ($q$) are regenerated at each timestep and can differ, leading to new attention maps and thus different visual content.
# 
# To mitigate this issue, the authors propose this nice idea: when only part of the prompt is updated, the cross-attention maps for the unchanged tokens should be preserved. This ensures that only the parts of the image corresponding to the modified text are affected, while the rest remains stable.
# 
# The figure below helps illustrate this idea:
# 

# <div style="text-align: center;">
#   <img src="blog_pics/prompt2prompt_2.png" alt="" width="600">
# </div>
# 

# Check out the [project page](https://prompt-to-prompt.github.io/), they showcase some really impressive results, along with a nice interactive [notebook](https://github.com/google/prompt-to-prompt/blob/main/prompt-to-prompt_stable.ipynb) you can try out yourself. To summarize, this method gives us a way to edit a generated image when slightly modifying the prompt, without causing the entire scene to change.
# 

# ### InstructPix2Pix: Learning to Follow Image Editing Instructions (CVPR 2023)
# 
# Prompt-to-Prompt is a powerful technique, but it comes with certain limitations. It works well when we are generating an image from a prompt and want to make small modifications by slightly changing the prompt. In this way, we can edit the generated image while preserving most of its structure. However, a key limitation is that the prompt changes need to be minimal. Moreover, Prompt-to-Prompt does not support editing **real** images, it only applies to images generated by the model itself. 
# 
# This is where InstructPix2Pix comes in. It leverages advances in prompt-to-promt method and large language models to enable image editing based on natural language instructions. This allows for more flexible edits, and it works on both synthetic and real images. See an example from the paper:
# 

# <div style="text-align: center;">
#   <img src="blog_pics/instruct_1.png" alt="" width="400">
# </div>

# The approach proposed by the authors is actually quite intuitive. They construct a dataset that consists of (instruction, input image, edited image) triplets, where the edited image reflects the instruction applied to the input image. Assuming we have this dataset, the model can be trained using standard conditional diffusion practices. As such, the model itself is a modified diffusion model that takes two conditioning signals:
# 1. The input image, which is added as an extra channel to the U-Net.
# 2. The instruction, which is encoded and used in cross-attention layers.
# 
# However, the challenge is that such a dataset does not exist. To solve this, the authors generate it automatically using Stable Diffusion, GPT-3 and Prompt-to-Prompt. Here's how the dataset is built:
# - Start with an input caption.
# - Use GPT-3 to generate:
#   - An edited caption (reflecting the desired change).
#   - An instruction describing how to get from the input to the edited caption.
# - Generate the input image from the input caption using Stable Diffusion.
# - Generate the edited image using the Prompt-to-Prompt method applied to the input and edited captions.
# 
# Finally, the model is trained to map from (input image + instruction) → edited image.
# Nice! See the figure below from the paper for clarification:
# 

# <div style="text-align: center;">
#   <img src="blog_pics/instruct_2.png" alt="" width="600">
# </div>
# 

# Note that, although the model is trained on syntheitc data, the authors show zero shot generalization to real images. Also see this [project](https://huggingface.co/blog/instruction-tuning-sd) generating nice results using this technique.

# ### Null-text Inversion for Editing Real Images using Guided Diffusion Models (CVPR 2023)
# 
# This paper introduces an approach for editing real images using the Prompt-to-Prompt method within guided diffusion models. The core idea is to associate a real image with a descriptive caption and then estimate a diffusion trajectory that could have produced this image from noise conditioned on that caption.
# 
# Think of it this way: if the image were synthetically generated, we would already have access to the initial latent variable and the diffusion trajectory. This would allow us to edit the image by modifying the prompt, using the Prompt-to-Prompt. However, since the image is real, we don’t have access to the original latent or its trajectory.
# 
# To solve this, the paper proposes a method for estimating the latent diffusion trajectory that maps the real image back into the noisy latent space. Once this trajectory is estimated, we can apply Prompt-to-Prompt editing just like with synthetic images. Check the figure below from the paper to see what the paper is about:
# 

# <div style="text-align: center;">
#   <img src="blog_pics/null_1.png" alt="" width="700">
# </div>
# 

# To understand this paper better, let's briefly recap two key concepts: **DDIM inversion** and **classifier-free guidance**.
# 
# **DDIM** (Denoising Diffusion Implicit Models) is an efficient sampling method used in diffusion models. It enables image generation from pure noise using significantly fewer steps than the original DDPM. Unlike DDPM, which is stochastic, DDIM provides a deterministic mapping from noise to image:
# $$
# z_{t-1} = \sqrt{\frac{\alpha_{t-1}}{\alpha_t}} z_t + \sqrt{\alpha_{t-1}} \left( \sqrt{\frac{1}{\alpha_{t-1}} - 1} - \sqrt{\frac{1}{\alpha_t} - 1} \right) \cdot \varepsilon_\theta(z_t)
# $$
# - $z_t$: the latent variable (e.g., noisy image) at timestep $t$
# - $z_{t-1}$: the denoised latent at the previous timestep
# - $\alpha_t$: the noise schedule coefficient at timestep $t$
# - $\varepsilon_\theta(z_t)$: the predicted noise at timestep $t$, estimated by the neural network $\theta$

# **DDIM inversion** is the reverse process of DDIM sampling. It maps a real image back into the latent space of the diffusion model:
# $$
# z_{t+1} = \sqrt{\frac{\alpha_{t+1}}{\alpha_t}} z_t + \sqrt{\alpha_{t+1}} \left( \sqrt{\frac{1}{\alpha_{t+1}} - 1} - \sqrt{\frac{1}{\alpha_t} - 1} \right) \cdot \varepsilon_\theta(z_t)
# $$
# 
# - $z_t$: the latent variable at timestep $t$ (obtained from the image)
# - $z_{t+1}$: the predicted latent at the next timestep
# - $\alpha_t$: the noise schedule coefficient at timestep $t$
# - $\varepsilon_\theta(z_t)$: the estimated noise from the model given $z_t$
# 
# Imagine we have generated an image using DDIM and want to modify it a bit. We could use DDIM inversion to go back to the latent, and regenerate the image using an updated prompt. It does not work so well, but still, it allows for some level of editing.

# 
# **Classifier-free guidance** is a technique that improves the alignment of the generated image with the given prompt. During sampling, it generates two outputs: one conditioned on the prompt (the *conditional* prediction) and another using an empty or "null" prompt (the *unconditional* prediction). The final result is a weighted combination of these two predictions, allowing control over how strongly the model follows the conditioning signal:
# 
# $$
# \tilde{\varepsilon}_\theta(z_t, t, \mathcal{C}, \emptyset) = w \cdot \varepsilon_\theta(z_t, t, \mathcal{C}) + (1 - w) \cdot \varepsilon_\theta(z_t, t, \emptyset)
# $$
# 
# - $z_t$: latent variable at timestep $t$
# - $t$: current timestep
# - $\mathcal{C}$: conditioning input (e.g., a text prompt)
# - $\emptyset$: null prompt
# - $w$: guidance scale parameter that controls the strength of conditioning
# - $\varepsilon_\theta(\cdot)$: the predicted noise by the model
# - $\tilde{\varepsilon}_\theta(\cdot)$: the guided noise prediction combining conditional and unconditional terms
# 
# By increasing $w$, the model gives more importance to the conditional prediction, enhancing prompt fidelity.
# 

# Now, I'm going to talk about the concepts a bit to help make things clearer. If we were to apply deterministic DDIM inversion to a *synthetic* image, we could recover the exact latent representation, since we have access to the full diffusion trajectory. However, in the case of a *real* image, we can only *estimate* the corresponding latent. In the figure above (under "DDIM Inversion"), you can see that the reconstruction is not perfect which is due to this issue. 
# 
# Nevertheless, the authors suggest that this estimated latent and its corresponding diffusion trajectory provide a good **starting point** or **pivot** for further editing using guided diffusion methods.
# 

# Another important point is that DDIM inversion has mostly been explored in the **unconditional** setting. However, when generating **conditional** samples, for example, using Stable Diffusion, we typically set the guidance scale to $w = 7.5$ to ensure the output aligns with the prompt. So, to estimate the reverse diffusion trajectory in a conditional setting, it might seem reasonable to also use $w > 1$. But the authors observe that doing so amplifies estimation errors and deteriorates the reconstruction quality. Refer back to the DDIM inversion formula: the noise prediction $\varepsilon_\theta$ is an estimate and inherently imperfect. When we scale it with $w > 1$, the error also gets amplified. As a result, the estimated noise vector may no longer follow a Gaussian distribution.  This is problematic because non-Gaussian noise lies outside the assumptions of our generative framework, meaning the resulting latent may no longer be editable via diffusion processes.
# 
# To summarize:
# - **$w = 1$** gives a meaningful and editable trajectory, but it's not optimal for achieving strong prompt alignment.
# - **$w > 1$** increases fidelity to the prompt, but may result in non-Gaussian noise that is difficult or impossible to edit.

# What is the solution then? First, they find a pivot trajectory $z^*$ using classifier-free guidance with $w = 1$. While $z^*$ may not be optimal for conditional generation, it provides a meaningful and editable starting point. So, they use this $z^*$ as an anchor. Next, they perform conditional sampling (e.g., with your prompt and classifier-free guidance using $w > 1$) and try to bring each latent step closer to $z^*$. This is formulated as an MSE objective, minimizing the distance between the conditional denoised latents and the pivot trajectory $z^*$ at each timestep.
# 
# But what’s being tuned here? Not the model itself (too expensive). Instead, the authors **tune the null-text embedding** (i.e., the embedding used when the prompt is empty). This allows the denoising path to be guided more precisely toward the pivot trajectory without altering the model weights. Check the method overview and algorithm from the paper for further clarification.

# <div style="text-align: center;">
#   <img src="blog_pics/null_2.png" alt="" width="500">
# </div>
# 

# <div style="text-align: center;">
#   <img src="blog_pics/null_3.png" alt="" width="500">
# </div>
# 

# Alright, I’ll stop here for now, there’s more to cover, so stay tuned for part 2!

# ### References
# - [Prompt-to-Prompt Image Editing with Cross-Attention Control (ICLR 2023)](https://arxiv.org/abs/2208.01626)
# - [InstructPix2Pix: Learning to Follow Image Editing Instructions (CVPR 2023)](https://arxiv.org/abs/2211.09800)
# - [Null-text Inversion for Editing Real Images using Guided Diffusion Models (CVPR 2023)](https://arxiv.org/abs/2211.09794)
# - [Hugging Face Diffusers Documentation](https://huggingface.co/docs/diffusers/en/index)
# - [Hugging Face Diffusion Course](https://huggingface.co/learn/diffusion-course/unit1/1)
#