#!/usr/bin/env python
# coding: utf-8
# # CS579: Lecture 05
# ** Community Detection **
#
# *[Dr. Aron Culotta](http://cs.iit.edu/~culotta)*
# *[Illinois Institute of Technology](http://iit.edu)*
#
# (Many figures come from [Mining of Massive Datasets](http://www.mmds.org/), Jure Leskovec, Anand Rajaraman, Jeff Ullman)
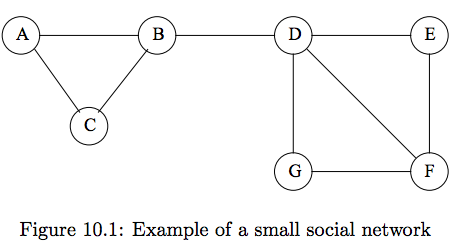
# 
#
# - **Why do we want to identify communities?**
# - **What are the "communities" in this graph?**
# - **Why did you choose these communities?**
#
#
# **A bad solution: Agglomerative clustering**
#
# - Let distance function $d(A,B)$ be the shortest path between nodes $A$ and $B$
# - Let $C_i$ and $C_j$ be two clusters of nodes. Then, let the distance between two clusters be the minimum distance of any two nodes: $d(C_i, C_j) = \min_{X \in C_i, Y \in C_j} \hspace{.1cm} d(X, Y)$
# - Greedy agglomerative clustering iterative merges the closest two clusters
#
#  # **What would agglomerative clustering do on this network? **
#
# 
#
# $d(A,B) = d(A,C) = d(B, C) = d(B,D) = d(D,E) = d(D,F) = d(D,G) = d(E,F) = d(G,F) = 1$
#
# $d(A,D) = d(C,D) ... = 2$
#
#
# **What would agglomerative clustering do on this network? **
#
# 
#
# $d(A,B) = d(A,C) = d(B, C) = d(B,D) = d(D,E) = d(D,F) = d(D,G) = d(E,F) = d(G,F) = 1$
#
# $d(A,D) = d(C,D) ... = 2$
#
#
# First merge: sample randomly from all nodes with distance == 1.
#
#
#
# So, $\frac{1}{9}$ chance we merge $B$ and $D$ in first merge.
#
# Not desireable...any other ideas?
#
# What makes the edge between $B$ and $D$ special?
#
#
# **Betweenness:** The betweenness of an edge $(A, B)$ is the number of shortest paths between any nodes $X$ and $Y$ that include edge $(A, B)$.
#
# High betweenness $\rightarrow$ $A$ and $B$ belong in different communities.
# 
#
#
# What is **betweenness** of $(B,D)$?
#
#
#
# > $(B,D)$ is on all shortest paths connecting any of $\{A,B,C\}$ to any of $\{D,E,F,G\}$.
#
# > Thus, total number of shortest paths = number passing through $(B,D)$ = $3 * 4 = \mathbf{12}.$. So, $bt(B,D) = 12$
#
#
#
# What is **betweenness** of $(D,F)$?
#
#
#
# > $(D,F)$ is on shortest paths from $\{A,B,C,D\}$ to $\{F\}$.
#
# > Thus, betweenness is $4 * 1 = \mathbf{4}.$
#
#
#
# Consider this graph:
#
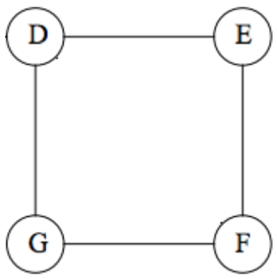
# 
#
# What is **betweenness** of $(D,G)$?
#
#
#
# > $(D,G)$ is on the shortest path from $D$ to $G$.
# > $(D,G)$ is also on one of the two shortest paths from $D$ to $F$ and $E$ to $G$.
#
# > Since there can be several shortest paths between two nodes, an edge (a, b) is credited with the fraction of those shortest paths that include the edge (a, b).
#
# > Thus, betweenness is $\frac{1}{2} + \frac{1}{2} + 1 = \mathbf{2}.$
# Formally:
#
# $$
# bt(e) =\sum_{s,t \in V} \frac{\sigma(s, t|e)}{\sigma(s, t)}
# $$
# where
#
# - $V$ is the set of nodes
# - $\sigma(s, t)$ is the number of shortest paths between nodes $s$ and $t$
# - $\sigma(s, t|e)$ is the number of those paths passing through some edge $e$
#
# If $s = t$, $\sigma(s, t) = 1$
#
# So, if there are two shortest paths between $s$ and $t$, but only one goes through $e$, betweenness only increases by 0.5.
#
#
#
# In[15]:
import networkx as nx
get_ipython().run_line_magic('matplotlib', 'inline')
def create_example_graph():
graph = nx.Graph()
graph.add_edges_from([('A', 'B'), ('A', 'C'), ('B', 'C'),
('B', 'D'), ('D', 'E'), ('D', 'F'),
('D', 'G'), ('E', 'F'), ('G', 'F')])
return graph
graph = create_example_graph()
nx.draw(graph, with_labels=True)
# In[16]:
# We'll use networkx's built-in betweenness computation in this example.
nx.edge_betweenness_centrality(graph, normalized=False)
# nx.edge_betweenness_centrality(graph, normalized=True)
# normalized between 0-1
# ** How to compute shortest path in undirected graph? **
#
#
# 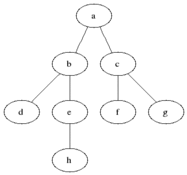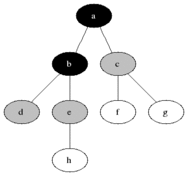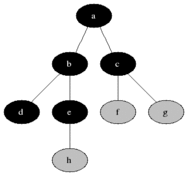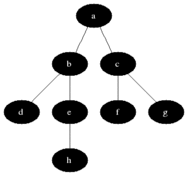 #
# [source](https://en.wikipedia.org/wiki/File:Animated_BFS.gif)
#
# ** Breadth first search: ** Given a sourse node $s$, compute the shortest paths to each of its neighbors. Proceed
# In[4]:
from collections import deque
# double ended queue
# stored as a doubly linked list
q = deque()
q.append(1)
print(q)
q.append(2)
print(q)
q.append(3)
print(q)
print('popleft returns: %d' % q.popleft())
print(q)
print('pop returns: %d' % q.pop())
print(q)
# In[5]:
# compare with:
a = [1,2,3]
print(a.pop(0))
#print(a.pop())
a
# **What is running time to remove first element of a dynamic array with $n$ elements (a list in Python)?**
#
#
#
# [source](https://en.wikipedia.org/wiki/File:Animated_BFS.gif)
#
# ** Breadth first search: ** Given a sourse node $s$, compute the shortest paths to each of its neighbors. Proceed
# In[4]:
from collections import deque
# double ended queue
# stored as a doubly linked list
q = deque()
q.append(1)
print(q)
q.append(2)
print(q)
q.append(3)
print(q)
print('popleft returns: %d' % q.popleft())
print(q)
print('pop returns: %d' % q.pop())
print(q)
# In[5]:
# compare with:
a = [1,2,3]
print(a.pop(0))
#print(a.pop())
a
# **What is running time to remove first element of a dynamic array with $n$ elements (a list in Python)?**
#
#
#
# $O(n)$: Need to shift all elements to the left.
#
#
#
# **What is the running time to remove first element of a doubly linked list $n$ elements (a deque in Python)?**
#
#
#
# $O(1)$
#
# See more:
# https://wiki.python.org/moin/TimeComplexity
#
# In[6]:
# Sample implementation of doubly linked list.
class Node:
def __init__(self, val):
self.val = val
self.prev = None # previous node
self.next = None # next node
self.head = self
def display(self):
node = self.head
vals = []
while node:
vals.append(node.val)
node = node.next
print(vals)
def popleft(self):
"""
Remove leftmost element of list.
"""
v = self.head.val
self.next.prev = None
self.head = self.next
return v
n1 = Node(1)
n2 = Node(2)
n3 = Node(3)
n1.next = n2
n2.prev = n1
n2.next = n3
n3.prev = n2
mylist = n1
mylist.display()
print(mylist.popleft())
print(mylist.popleft())
# In[17]:
# to get the neighbors of a node:
list(graph.neighbors('A'))
# vs
#graph.neighbors('A')
# In[8]:
nx.draw(graph, with_labels=True)
# In[9]:
def bfs(graph, start):
"""
Return the order in which nodes are visited in a breadth-first
traversal, starting with the given node.
"""
q = deque()
q.append(start)
seen = set() # nodes we have already visited.
res = []
while len(q) > 0: # while more to visit
n = q.popleft()
if n not in seen:
res.append(n)
seen.add(n)
for nn in graph.neighbors(n):
if nn not in seen:
q.append(nn)
return res
bfs(graph, 'D')
# To get all shortest paths from a node, perform BFS, while keeping track of the depth of the search.
# In[18]:
for s in graph.nodes():
paths = nx.single_source_shortest_path(graph, s)
print('\nshortest paths for %s' % s)
print(paths)
# # Girvan-Newman Algorithm
#
# **Input:** Graph $G$; desired number of clusters $k$
#
# **Output:** A hierarchical clustering of nodes, based on edge betweenness
#
# - **While** number of clusters $< k$:
# - Compute the betweenness of all edges in $G$
# - Remove edge with highest betweenness
#
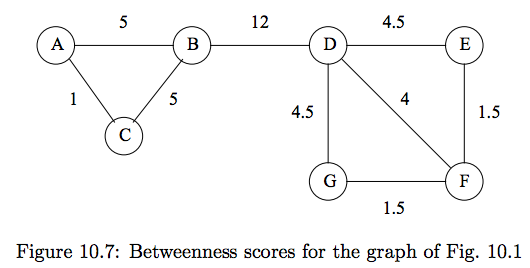
# 
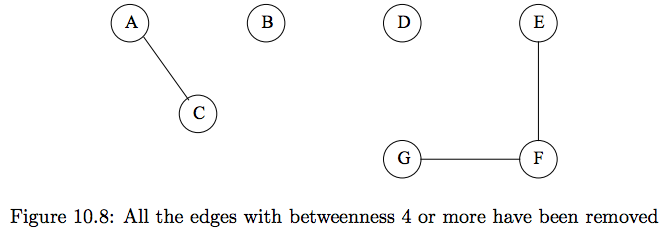
# 
# ## Computing betweenness of all edges
#
# - All pairs-shortest-paths, but need to store the paths.
# - How can we reduce redundant computation?
# ## Computing betweenness of all edges
#
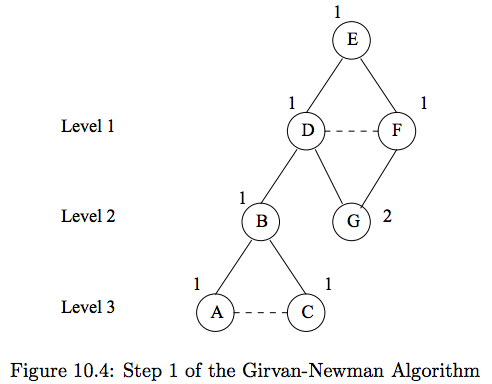
# 
#
# 1.) Do breadth-first search starting at node $E$.
# - Each level is length of shortest path from $E$ to that node
# - Edges within the same level cannot be part of a shortest path from $E$ to some target.
#
# 2.) Label each node by the number of shortest paths that reach it from the root.
# - Start by labeling the root ($E$). Then, each child node is the sum of its parents.
# - E.g., $G = D + F$
#
# ## Computing betweenness of all edges
#
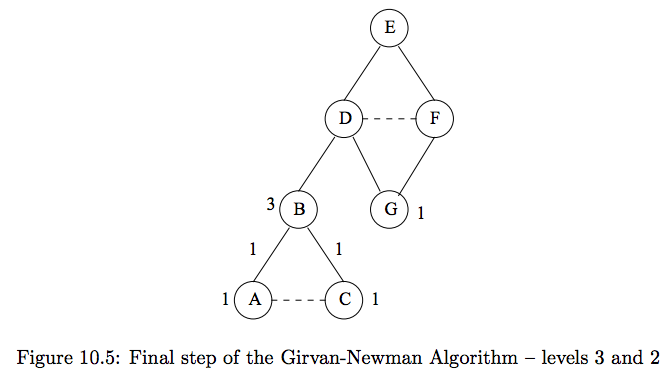
# 
#
# 3.) Compute fraction of shortest paths through each edge (bottom up).
# - leaf nodes get credit 1
# - non-leaf nodes get credit of 1 + credits for edges to nodes at level below
# - edges to level above gets credit proportional to fraction of shortest paths that go through it.
#
# E.g. Level 3:
# - $A$ and $C$ are given credit 1 (they are leaf nodes)
#
# Level 2:
# - $B$ gets credit $3$ ($A + C + 1$)
# - All shortest paths from $\{E\}$ to $\{A, B, C\}$ go through B.
# - $G$ gets credit 1 (leaf)
#
# ## Computing betweenness of all edges
#
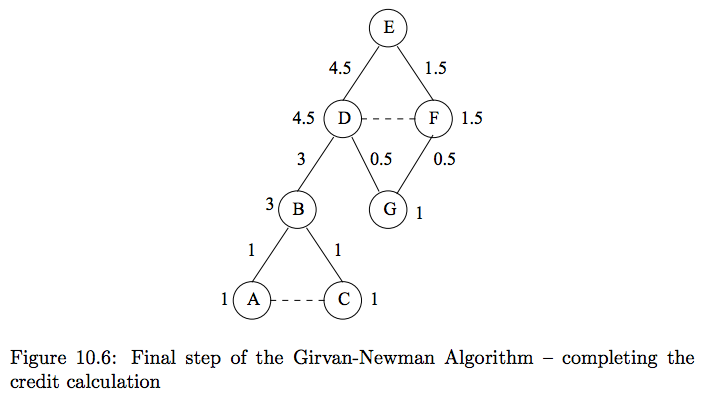
# 
#
# Level 1 Edges:
# - $D,B$ edge gets all credit from node $B$ (3)
# - $G$ has two parents, so edges $(D,G)$, $(F,G)$ share the credit from $G$
# - From step 1, $D$ and $F$ each have credit 1, so shared equally. $(\frac{1}{1+1} = .5)$
# - What if $D=5$, $F=3$? $\frac{5}{8}$, $\frac{3}{8}$
#
#
# Level 1 Nodes:
# - $D = 1 + 3 + .5 = 4.5$
# - $F = 1 + .5 = 1.5$
# ## Computing betweenness of all edges
#
# 
#
# - What if $D=5$, $F=3$?
#
# ## Computing betweenness of all edges
#
# 
#
# - What if $D=5$, $F=3$?
# $(D,G) = \frac{5}{8}$, $(F,G) = \frac{3}{8}$
# Final steps:
#
# - Repeat for each node as source
# - Divide total by 2 (since each shortest path found twice, once in each direction)
#
# 
# **More detailed example for edge (D,E):**
#
# For each root node, we report the value computed for edge (D,E) for Girvan Newman:
#
# | root node | value for (D,E)|
# |-----------|----------------|
# | A | 1 |
# | B | 1 |
# | C | 1 |
# | D | 1 |
# | E | 4.5 |
# | F | 0 |
# | G | .5 |
# | **total** | 9 |
#
# We then divide by 2 to get the final betweenness of (D,E), 4.5.
#
#
# The reason the value is $1$ when the root node is one of ${A,B,C}$ is that $E$ will be a leaf node for each of these. (Shortest paths to $F$ or $G$ from $A,B,C$ will never traverse edge $(D,E)$). The value is 0.5 for $G$ as source, becasue half credit is given as there are two shortest paths of length 2 from $G$ to $E$, but only one traverses $(D,E)$. No other shortest path from root $G$ traverses $(D,E)$.
#
# In[11]:
nx.edge_betweenness_centrality(graph, normalized=False)
# In[12]:
def girvan_newman(G, depth=0):
""" Recursive implementation of the girvan_newman algorithm.
See http://www-rohan.sdsu.edu/~gawron/python_for_ss/course_core/book_draft/Social_Networks/Networkx.html
Args:
G.....a networkx graph
Returns:
A list of all discovered communities,
a list of lists of nodes. """
if G.order() == 1:
return [G.nodes()]
def find_best_edge(G0):
eb = nx.edge_betweenness_centrality(G0)
# eb is dict of (edge, score) pairs, where higher is better
# Return the edge with the highest score.
return sorted(eb.items(), key=lambda x: x[1], reverse=True)[0][0]
# Each component is a separate community. We cluster each of these.
components = [c for c in nx.connected_component_subgraphs(G)]
indent = ' ' * depth # for printing
while len(components) == 1:
edge_to_remove = find_best_edge(G)
print(indent + 'removing ' + str(edge_to_remove))
G.remove_edge(*edge_to_remove)
components = [c for c in nx.connected_component_subgraphs(G)]
result = [c.nodes() for c in components]
print(indent + 'components=' + str(result))
for c in components:
result.extend(girvan_newman(c, depth + 1))
return result
# In[13]:
result = girvan_newman(create_example_graph())
# In[14]:
result
# In[1]:
from IPython.core.display import HTML
HTML(open('../custom.css').read())
 #
# [source](https://en.wikipedia.org/wiki/File:Animated_BFS.gif)
#
# ** Breadth first search: ** Given a sourse node $s$, compute the shortest paths to each of its neighbors. Proceed
# In[4]:
from collections import deque
# double ended queue
# stored as a doubly linked list
q = deque()
q.append(1)
print(q)
q.append(2)
print(q)
q.append(3)
print(q)
print('popleft returns: %d' % q.popleft())
print(q)
print('pop returns: %d' % q.pop())
print(q)
# In[5]:
# compare with:
a = [1,2,3]
print(a.pop(0))
#print(a.pop())
a
# **What is running time to remove first element of a dynamic array with $n$ elements (a list in Python)?**
#
#
#
# [source](https://en.wikipedia.org/wiki/File:Animated_BFS.gif)
#
# ** Breadth first search: ** Given a sourse node $s$, compute the shortest paths to each of its neighbors. Proceed
# In[4]:
from collections import deque
# double ended queue
# stored as a doubly linked list
q = deque()
q.append(1)
print(q)
q.append(2)
print(q)
q.append(3)
print(q)
print('popleft returns: %d' % q.popleft())
print(q)
print('pop returns: %d' % q.pop())
print(q)
# In[5]:
# compare with:
a = [1,2,3]
print(a.pop(0))
#print(a.pop())
a
# **What is running time to remove first element of a dynamic array with $n$ elements (a list in Python)?**
#
#