#!/usr/bin/env python
# coding: utf-8

# # CS579: Lecture 12  
# 
# ** Demographic Inference I**
# 
# *[Dr. Aron Culotta](http://cs.iit.edu/~culotta)*  
# *[Illinois Institute of Technology](http://iit.edu)*

# **dem·o·graph·ics**
# 
# statistical data relating to the population and particular groups within it.
# 
# E.g., age, ethnicity, gender, income, ...

# # Why Demographics?
# 
# - Marketing
#   - Who are my customers?
#   - Who are my competitors' customers?
#   - E.g., [DemographicsPro](http://www.demographicspro.com/samples#c=%40FamilyGuyonFOX)
#   
# - Social Media as Surveys
#   - E.g., 45% of tweets express positive sentiment toward Pres. Obama
#   - Who wrote those tweets?
#   
# - Health
#   - 2% of Facebook users are expressing flu-like symptoms
#   - Are they representative of the full population?
# 
# 

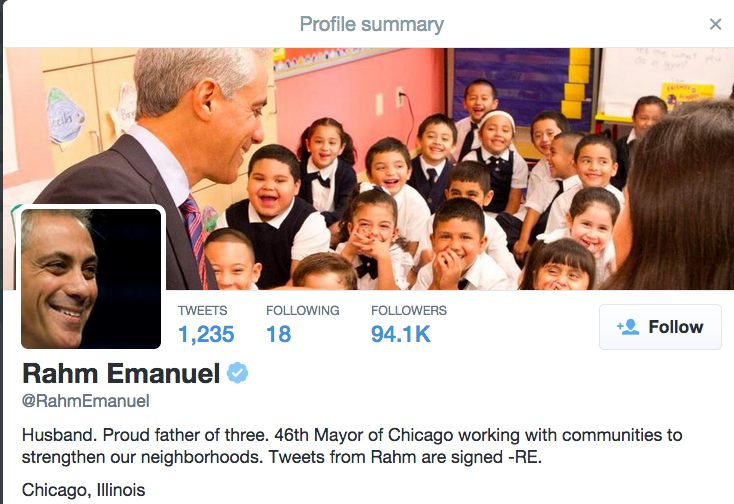
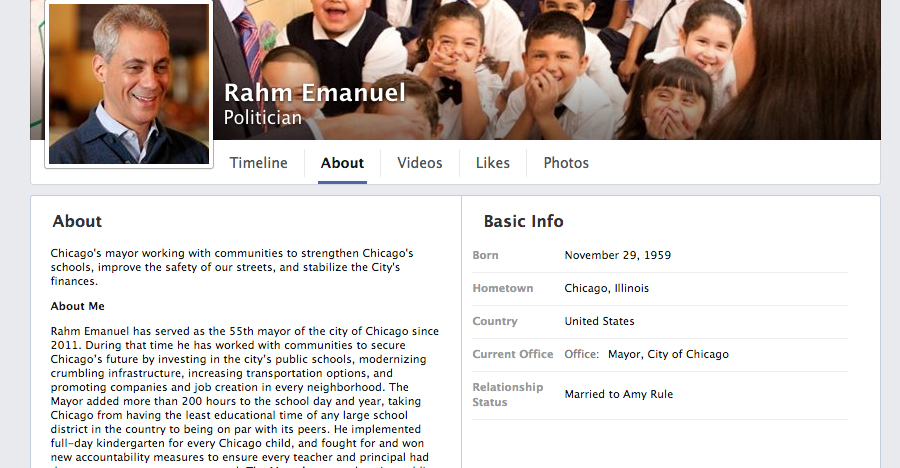
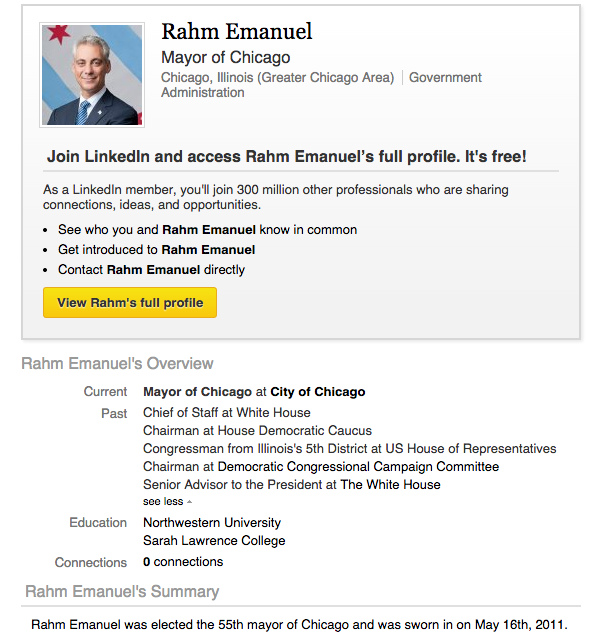
# ** User profiles vary from site to site. **

# ![rahm](rahm.png)

# ![rahm-fb](rahm-fb.png)

# ![rahm-li](rahm-li.png)

# # Approaches
# 
# - Clever use of external data
#   - E.g., U.S. Census name lists for gender
# - Look for keywords in profile
#   - "African American Male"
#   - "Happy 21st birthday to me"
# - Machine Learning

# In[2]:


# Guessing gender
# Collect 1000 tweets matching query "i"
import configparser
import sys
from TwitterAPI import TwitterAPI

def get_twitter(config_file):
    """ Read the config_file and construct an instance of TwitterAPI.
    Args:
      config_file ... A config file in ConfigParser format with Twitter credentials
    Returns:
      An instance of TwitterAPI.
    """
    config = configparser.ConfigParser()
    config.read(config_file)
    twitter = TwitterAPI(
                   config.get('twitter', 'consumer_key'),
                   config.get('twitter', 'consumer_secret'),
                   config.get('twitter', 'access_token'),
                   config.get('twitter', 'access_token_secret'))
    return twitter

twitter = get_twitter('twitter.cfg')
tweets = []
n_tweets=1000
for r in twitter.request('statuses/filter', {'track': 'i'}):
    tweets.append(r)
    if len(tweets) % 100 == 0:
        print('%d tweets' % len(tweets))
    if len(tweets) >= n_tweets:
        break
print('fetched %d tweets' % len(tweets))


# In[3]:


# not all tweets are returned
# https://dev.twitter.com/streaming/overview/messages-types#limit_notices
[t for t in tweets if 'user' not in t][:6]


# In[4]:


# restrict to actual tweets
# (remove "deleted" tweets)
tweets = [t for t in tweets if 'user' in t]
print('fetched %d tweets' % len(tweets))


# In[5]:


# Print last 10 names.
names = [t['user']['name'] for t in tweets]
names[-10:]


# In[6]:


# Fetch census name data from:
# http://www2.census.gov/topics/genealogy/1990surnames/
import requests
from pprint import pprint
males_url = 'http://www2.census.gov/topics/genealogy/' + \
            '1990surnames/dist.male.first'
females_url = 'http://www2.census.gov/topics/genealogy/' + \
              '1990surnames/dist.female.first'
males = requests.get(males_url).text.split('\n')
females = requests.get(females_url).text.split('\n')
print('males:')
pprint(males[:10])
print('females:')
pprint(females[:10])


# In[7]:


# Get names. 
male_names = set([m.split()[0].lower() for m in males if m])
female_names = set([f.split()[0].lower() for f in females if f])
print('%d male and %d female names' % (len(male_names), len(female_names)))
print('males:\n' + '\n'.join(list(male_names)[:10]))
print('\nfemales:\n' + '\n'.join(list(female_names)[:10]))


# In[8]:


# Initialize gender of all tweets to unknown.
for t in tweets:
    t['gender'] = 'unknown'


# In[9]:


# label a Twitter user's gender by matching name list.
import re
def gender_by_name(tweets, male_names, female_names):
    for t in tweets:
        name = t['user']['name']
        if name:
            # remove punctuation.
            name_parts = re.findall('\w+', name.split()[0].lower())
            if len(name_parts) > 0:
                first = name_parts[0].lower()
                if first in male_names:
                    t['gender'] = 'male'
                elif first in female_names:
                    t['gender'] = 'female'
                else:
                    t['gender'] = 'unknown'

gender_by_name(tweets, male_names, female_names)
# What's wrong with this approach?


# In[10]:


from collections import Counter

def print_genders(tweets):
    counts = Counter([t['gender'] for t in tweets])
    print('%.2f of accounts are labeled with gender' % 
          ((counts['male'] + counts['female']) / sum(counts.values())))
    print('gender counts:\n', counts)
    for t in tweets[:20]:
        print(t['gender'], t['user']['name'])
    
print_genders(tweets)


# In[11]:


# What about ambiguous names?
def print_ambiguous_names(male_names, female_names):
    ambiguous = [n for n in male_names if n in female_names]  # names on both lists
    print('found %d ambiguous names:\n'% len(ambiguous))
    print('\n'.join(ambiguous[:20]))
    
print_ambiguous_names(male_names, female_names)


# In[12]:


# Keep names that are more frequent in one gender than the other.
def get_percents(name_list):
    # parse raw data to extract, e.g., the percent of males names John.
    return dict([(n.split()[0].lower(), float(n.split()[1]))
                  for n in name_list if n])

males_pct = get_percents(males)
females_pct = get_percents(females)

# Assign a name as male if it is more common among males than femals.
male_names = set([m for m in male_names if m not in female_names or
              males_pct[m] > females_pct[m]])
female_names = set([f for f in female_names if f not in male_names or
              females_pct[f] > males_pct[f]])

print_ambiguous_names(male_names, female_names)
print('%d male and %d female names' % (len(male_names), len(female_names)))


# In[13]:


# Relabel twitter users (compare with above)
gender_by_name(tweets, male_names, female_names)
print_genders(tweets)


# In[14]:


# Who are the unknowns?
# "Filtered" data can have big impact on analysis.
unknown_names = Counter(t['user']['name']
                        for t in tweets if t['gender'] == 'unknown')
unknown_names.most_common(20)


# In[28]:


# How do the profiles of male Twitter users differ from
# those of female users?

male_profiles = [t['user']['description'] for t in tweets
                if t['gender'] == 'male']

female_profiles = [t['user']['description'] for t in tweets
                if t['gender'] == 'female']
#male_profiles = [t['text'] for t in tweets
#                if t['gender'] == 'male']

#female_profiles = [t['text'] for t in tweets
#                if t['gender'] == 'female']

import re
def tokenize(s):
    return re.sub('\W+', ' ', s).lower().split() if s else []

male_words = Counter()
female_words = Counter()

for p in male_profiles:
    male_words.update(Counter(tokenize(p)))
                      
for p in female_profiles:
    female_words.update(Counter(tokenize(p)))

print('Most Common Male Terms:')
pprint(male_words.most_common(10))
    
print('\nMost Common Female Terms:')
pprint(female_words.most_common(10))


# In[29]:


print(len(male_words))
print(len(female_words))


# In[30]:


# Compute difference
diff_counts = dict([(w, female_words[w] - male_words[w])
                    for w in
                    set(female_words.keys()) | set(male_words.keys())])

sorted_diffs = sorted(diff_counts.items(), key=lambda x: x[1])

print('Top Male Terms (diff):')
pprint(sorted_diffs[:10])

print('\nTop Female Terms (diff):')
pprint(sorted_diffs[-10:])


# ** A problem with difference of counts:**
# 
# <br><br><br><br>
# What if we have more male than female words in total?
# 
# <br><br><br><br>
# Instead, consider "the probability that a male user writes the word **w**"
# 
# <br><br><br><br>
# 
# $$p(w|male) = \frac{freq(w, male)}
# {\sum_i freq(w_i, male)} $$

# ** Odds Ratio (OR)**
# 
# The ratio of the probabilities for a word from each class:
# 
# $$ OR(w) = \frac{p(w|female)}{p(w|male)} $$
# 
# 
# - High values --> more likely to be written by females
# - Low values --> more likely to be written by males
# 

# In[31]:


def counts_to_probs(gender_words):
    """ Compute probability of each term according to the frequency
    in a gender. """
    total = sum(gender_words.values())
    return dict([(word, count / total)
                 for word, count in gender_words.items()])

male_probs = counts_to_probs(male_words)
female_probs = counts_to_probs(female_words)

print('p(w|male)')
pprint(sorted(male_probs.items(), key=lambda x: -x[1])[:10])

print('\np(w|female)')
pprint(sorted(female_probs.items(), key=lambda x: -x[1])[:10])


# In[32]:


def odds_ratios(male_probs, female_probs):
    return dict([(w, female_probs[w] / male_probs[w])
                 for w in
                 set(male_probs) | set(female_probs)])

ors = odds_ratios(male_probs, female_probs)


# In[38]:


print(len(male_probs))
print(len(female_probs))
female_but_not_male = set(female_probs) - set(male_probs)
print('%d words in female_probs but not in male_probs' % len(female_but_not_male))
fem_word = list(female_but_not_male)[-10]
print(fem_word)
print(female_probs[fem_word])
#'selfcare' in male_probs


# ** How to deal with 0-probabilities? **
# 
# $$p(w|male) = \frac{freq(w, male)}
# {\sum_i freq(w_i, male)} $$
# 
# $freq(w, male) = 0$
# 
# Do we really believe there is **0** probability of a male using this term?
# 
# (Recall over-fitting discussion.)
# <br><br><br><br>

# ** Additive Smoothing **
# 
# Reserve small amount of counts (e.g., 1) for unseen observations.
# 
# E.g., assume we've seen each word at least once in each class.
# 
# $$p(w|male) = \frac{1 + freq(w, male)}
# {|W| + \sum_i freq(w_i, male)} $$
# 
# $|W|$: number of unique words.

# In[39]:


# Additive smoothing. Add count of 1 for all words.
all_words = set(male_words) | set(female_words)
male_words.update(all_words)  
female_words.update(all_words)

male_probs = counts_to_probs(male_words)
female_probs = counts_to_probs(female_words)
print('\n'.join(str(x) for x in 
                sorted(male_probs.items(), key=lambda x: -x[1])[:10]))


# In[41]:


# Even though word doesn't appear, has non-zero probability.
print(male_probs[fem_word])


# In[42]:


ors = odds_ratios(male_probs, female_probs)

sorted_ors = sorted(ors.items(), key=lambda x: -x[1])

print('Top Female Terms (OR):')
pprint(sorted_ors[:20])

print('\nTop Male Terms (OR):')
pprint(sorted_ors[-20:])