#!/usr/bin/env python
# coding: utf-8

# This notebook is meant to be viewed as a [RISE](https://github.com/damianavila/RISE) slideshow. When run, a custom stylesheet will be applied:
# * *italic* text will be shown in *blue*,
# * **bold** text will be showin in **red**, and
# * ~~strikethrough~~ text will be shown in ~~green~~.
# 
# The code below is meant to be run before the presentation to ensure that Sage and its dependencies are properly initialized, so no waiting is required during the presentation.

# In[ ]:


import drg
p = [[[1, 0, 0, 0], [0, 6, 0, 0], [0, 0, 3, 0], [0, 0, 0, 6]],
     [[0, 1, 0, 0], [1, 2, 1, 2], [0, 1, 0, 2], [0, 2, 2, 2]],
     [[0, 0, 1, 0], [0, 2, 0, 4], [1, 0, 2, 0], [0, 4, 0, 2]],
     [[0, 0, 0, 1], [0, 2, 2, 2], [0, 2, 0, 1], [1, 2, 1, 2]]]
scheme = drg.ASParameters(p)
scheme.kreinParameters()


# # Computing distance-regular graph and association scheme parameters in SageMath with [`sage-drg`](https://github.com/jaanos/sage-drg)
# 
# ### Janoš Vidali
# #### University of Ljubljana
# 
# <br />
# 
# <img src="qrcode.png" align="right" />
# 
# <br />
# 
# [Live slides](https://mybinder.org/v2/gh/jaanos/sage-drg/master?filepath=jupyter/2019-07-04-fpsac/FPSAC-sage-drg.ipynb) on [Binder](https://mybinder.org)
# 
# https://github.com/jaanos/sage-drg

# ## Association schemes
# 
# * **Association schemes** were defined by *Bose* and *Shimamoto* in *1952* as a theory underlying **experimental design**.
# * They provide a ~~unified approach~~ to many topics, such as
#   - *combinatorial designs*,
#   - *coding theory*,
#   - generalizing *groups*, and
#   - *strongly regular* and *distance-regular graphs*.

# ## Examples
# 
# * *Hamming schemes*: **$X = \mathbb{Z}_n^d$**, **$x \ R_i \ y \Leftrightarrow \operatorname{weight}(x-y) = i$**
# * *Johnson schemes*: **$X = \{S \subseteq \mathbb{Z}_n \;|\; |S| = d\}$** ($2d \le n$), **$x \ R_i \ y \Leftrightarrow |x \cap y| = d-i$**
# 
# <center><img src="as.png" /></center>

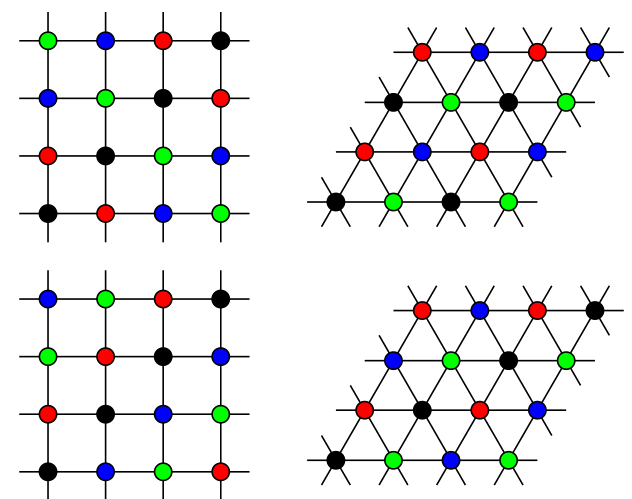# ## Definition
# 
# * Let **$X$** be a set of *vertices* and **$\mathcal{R} = \{R_0 = \operatorname{id}_X, R_1, \dots, R_D\}$** a set of *symmetric relations* partitioning *$X^2$*.
# 
# * **$(X, \mathcal{R})$** is said to be a **$D$-class association scheme** if there exist numbers **$p^h_{ij}$** ($0 \le h, i, j \le D$) such that, for any *$x, y \in X$*,
# **$$
# x \ R_h \ y \Rightarrow |\{z \in X \;|\; x \ R_i \ z \ R_j \ y\}| = p^h_{ij}
# $$**
# 
# * We call the numbers **$p^h_{ij}$** ($0 \le h, i, j \le D$) **intersection numbers**.

# ## Main problem
# 
# * Does an association scheme with given parameters ~~exist~~?
#   - If so, is it ~~unique~~?
#   - Can we determine ~~all~~ such schemes?
# * ~~Lists~~ of feasible parameter sets have been compiled for [**strongly regular**](https://www.win.tue.nl/~aeb/graphs/srg/srgtab.html) and [**distance-regular graphs**](https://www.win.tue.nl/~aeb/drg/drgtables.html).
# * Recently, lists have also been compiled for some [**$Q$-polynomial association schemes**](http://www.uwyo.edu/jwilliford/).
# * Computer software allows us to *efficiently* compute parameters and check for *existence conditions*, and also to obtain new information which would be helpful in the ~~construction~~ of new examples.

# ## Bose-Mesner algebra
# 
# * Let **$A_i$** be the *binary matrix* corresponding to the relation *$R_i$* ($0 \le i \le D$).
# 
# * The vector space **$\mathcal{M}$** over *$\mathbb{R}$* spanned by *$A_i$* ($0 \le i \le D$) is called the **Bose-Mesner algebra**.
# 
# * *$\mathcal{M}$* has a second basis ~~$\{E_0, E_1, \dots, E_D\}$~~ consisting of *projectors* to the *common eigenspaces* of *$A_i$* ($0 \le i \le D$).
# 
# * There are ~~nonnegative~~ constants **$q^h_{ij}$**, called **Krein parameters**, such that
# **$$
# E_i \circ E_j = {1 \over |X|} \sum_{h=0}^d q^h_{ij} E_h ,
# $$**
# where **$\circ$** is the *entrywise matrix product*.

# ## Parameter computation: general association schemes

# In[ ]:


get_ipython().run_line_magic('display', 'latex')
import drg
p = [[[1, 0, 0, 0], [0, 6, 0, 0], [0, 0, 3, 0], [0, 0, 0, 6]],
     [[0, 1, 0, 0], [1, 2, 1, 2], [0, 1, 0, 2], [0, 2, 2, 2]],
     [[0, 0, 1, 0], [0, 2, 0, 4], [1, 0, 2, 0], [0, 4, 0, 2]],
     [[0, 0, 0, 1], [0, 2, 2, 2], [0, 2, 0, 1], [1, 2, 1, 2]]]
scheme = drg.ASParameters(p)
scheme.kreinParameters()


# ## Metric and cometric schemes
# 
# * If **$p^h_{ij} \ne 0$** (resp. **$q^h_{ij} \ne 0$**) implies **$|i-j| \le h \le i+j$**, then the association scheme is said to be **metric** (resp. **cometric**).
# 
# * The *parameters* of a *metric* association scheme can be ~~determined~~ from the **intersection array**
# *$$
# \{b_0, b_1, \dots, b_{D-1}; c_1, c_2, \dots, c_D\}
# \quad (b_i = p^i_{1,i+1}, c_i = p^i_{1,i-1}).
# $$*
# 
# * The *parameters* of a *cometric* association scheme can be ~~determined~~ from the **Krein array**
# *$$
# \{b^*_0, b^*_1, \dots, b^*_{D-1}; c^*_1, c^*_2, \dots, c^*_D\}
# \quad (b^*_i = q^i_{1,i+1}, c^*_i = q^i_{1,i-1}).
# $$*
# 
# * *Metric* association schemes correspond to *distance-regular graphs*.

# ## Parameter computation: metric and cometric schemes

# In[ ]:


from drg import DRGParameters
syl = DRGParameters([5, 4, 2], [1, 1, 4])
syl


# In[ ]:


syl.order()


# In[ ]:


from drg import QPolyParameters
q225 = QPolyParameters([24, 20, 36/11], [1, 30/11, 24])
q225


# In[ ]:


q225.order()


# In[ ]:


syl.pTable()


# In[ ]:


syl.kreinParameters()


# In[ ]:


syl.distancePartition()


# In[ ]:


syl.distancePartition(1)


# ## Parameter computation: parameters with variables
# 
# Let us define a *one-parametric family* of *intersection arrays*.

# In[ ]:


r = var("r")
f = DRGParameters([2*r^2*(2*r+1), (2*r-1)*(2*r^2+r+1), 2*r^2], [1, 2*r^2, r*(4*r^2-1)])
f


# In[ ]:


f1 = f.subs(r == 1)
f1


# The parameters of `f1` are known to ~~uniquely determine~~ the *Hamming scheme $H(3, 3)$*.

# In[ ]:


f2 = f.subs(r == 2)
f2


# ## Feasibility checking
# 
# A parameter set is called **feasible** if it passes all known *existence conditions*.

# Let us verify that *$H(3, 3)$* is feasible.

# In[ ]:


f1.check_feasible()


# No error has occured, since all existence conditions are met.

# Let us now check whether the second member of the family is feasible.

# In[ ]:


f2.check_feasible()


# In this case, ~~nonexistence~~ has been shown by *matching* the parameters against a list of **nonexistent families**.

# ## Triple intersection numbers
# 
# * In some cases, **triple intersection numbers** can be computed.
# * ~~Nonexistence~~ of some *$Q$-polynomial* association schemes has been proven by obtaining a *contradiction* in *double counting* with triple intersection numbers.

# In[ ]:


q225.check_quadruples()


# *Integer linear programming* has been used to find solutions to multiple systems of *linear Diophantine equations*,
# *eliminating* inconsistent solutions.