#!/usr/bin/env python
# coding: utf-8

# <div>
# <img src="https://discuss.pytorch.org/uploads/default/original/2X/3/35226d9fbc661ced1c5d17e374638389178c3176.png" width="400" style="margin: 50px auto; display: block; position: relative; left: -30px;" />
# </div>
# 
# <!--NAVIGATION-->
# # < [Optimization](4-Optimization.ipynb) | Modules | [CNN](6-CNN.ipynb) >

# ### PyTorch Modules
# 
# Modules are a way to build re-usable model components and to manage model parameters.
# PyTorch has many built-in modules for common operations like convolutions, recurrent neural networks, max pooling, common activation functions, etc.
# You can also build your own modules.
# 
# This notenook introduces modules, and you will build a small neural network to perform image classification on MNIST.
# 
# ### Table of Contents
# #### 1. [Modules](#Modules)
# #### 2. [Building and Training a Neural Network](#Building-and-Training-a-Neural-Network)

# ---

# In[ ]:


import torch
import matplotlib.pyplot as plt


# ---

# # Modules

# ## Modules and parameters
# 
# They help to
# - keep track of the parameters in your model.
# - save/load of your model.
# - reset gradients (with `model.zero_grad()`)
# - move all parameters to the gpu (with `model.to(device)`)
# 
# The module's parameters are represented by `torch.nn.Parameter` objects.  
# A `Parameter` is a tensor:
# - with `requires_grad` set to `True` by default,
# - which is automatically added to the list of parameters when used within a module.
# 
# If you are interested, you can have a look at the [torch.nn.Parameter documentation](https://pytorch.org/docs/stable/_modules/torch/nn/parameter.html).

# **Example**  
# A `torch.nn.Linear` module has two parameters `weight` and `bias` .  
# You can access the parameters with their names:

# In[ ]:


module = torch.nn.Linear(5, 2)  # 5 input dimensions, 2 output dimensions


# In[ ]:


print("weight:", module.weight)
print("\nbias:", module.bias)


# You can also get a list of all the parameters of the network using the `.parameters()` function.  

# In[ ]:


for param in module.parameters():
    print("\n", param)


# Each instance of a model has its own parameters.  
# The parameters are initialized randomly when the model is instantiated.

# In[ ]:


linear_regression_model = torch.nn.Linear(5, 2)
linear_regression_model.weight  # each time you run this cell, you'll see different outputs


# **Exercice**  
# Explore the parameters of the `torch.nn.Conv1D` module.

# In[ ]:


# YOUR TURN


# ---
# 

# ## Basic usage
# 

# In[ ]:


linear_model = torch.nn.Linear(5, 2)  # 5 input dimensions, 2 output dimensions


# **Working with batches**  
# Modules always operate on __batches__ of data. If a module is designed to operate on datapoints with 5 features, the shape of the module's inputs will be `(batch, 5)`. This allows us to process multiple datapoints in parallel and increase efficiency.

# In[ ]:


batch_size = 3
feature_size = 5

x = torch.randn(batch_size, feature_size)
print("x = {}".format(x))


# **Calling the model**  
# You can __call__ the model on an input (forward pass) using the `module(input)` syntax.  
# This evaluation uses the current model parameters.

# In[ ]:


predicted_y = linear_model(x)

print(predicted_y)


# ---

# ## Composing modules with `torch.nn.Sequential`
# 
# If the model you want to build is a simple chain of other modules, you can compose them using `torch.nn.Sequential`:

# In[ ]:


neural_net = torch.nn.Sequential(
    torch.nn.Linear(5, 10),
    torch.nn.ReLU(),
    torch.nn.Linear(10, 2),
)

# Run the model:
neural_net(x)


# In[ ]:


for name, tensor in neural_net.named_parameters():  # Here we use a sligtly different version of the parameters() function
    print("{:10s} shape = {}".format(name, tensor.shape))  # which also returns the parameter name


# ---

# ## Custom modules

# A module has to implement two functions:
# 
# - the `__init__` function, where you define all the sub-components that have learnable parameters. This makes sure that your module becomes aware all its parameters. The sub-components (layers) do not need to be defined in order of execution or connceted together. Don't forget to initialize the parent class `torch.nn.Module` with `super().__init__()`.
# 
# 
# - the `forward` function, which is the method that defines what has to be executed during the forward pass and especially how the layers are connected. This is where you call the layers that you defined inside `__init__`.
# 

# In[ ]:


# This is the most basic form of a custom module:
class MySimpleModule(torch.nn.Module):
    def __init__(self, input_size, num_classes):
        super().__init__()
        
        # Define sub-modules or parameters
        # torch.nn.Module takes care of adding their parameters to your new module
        self.linear = torch.nn.Linear(input_size, num_classes)
        self.relu = torch.nn.ReLU()
    
    def forward(self, x):
        out = self.linear(x)
        out_relu = self.relu(out)
        return out_relu


# You can use the `print` function to list a module's submodules:

# In[ ]:


model = MySimpleModule(input_size=20, num_classes=5)
print(model)


# ---

# # Building and Training a Neural Network

# It's time to implement a neural network now. In this section, you will learn to classify handwritten digits from the widely known MNIST dataset.
# The dataset consists of 60,000 training images of size 28x28, and another 10,000 images for evaluating the quality of the trained model.

# ![MNIST](figures/mnist.jpeg)

# ## Loading the dataset
# 
# MNIST is widely used and a dataset and it is available in the `torchvision` library.

# In[ ]:


import torchvision

# MNIST Dataset (Images and Labels)
train_dataset = torchvision.datasets.MNIST(
    root='./data',
    train=True,
    transform=torchvision.transforms.ToTensor(),
    download=True
)
test_dataset = torchvision.datasets.MNIST(
    root='./data',
    train=False,
    transform=torchvision.transforms.ToTensor(),
    download=True
)


# __Exercise__<br>
# Verify how many images there are in the training dataset. How is one training example represented? What is the type and shape of an entry from the dataset?

# In[ ]:


# YOUR TURN


# When we train a model, we make multiple passes - called epoch - through all the examples in the training set.  
# Each pass, the data points are shuffled and batched together. For this purpose, we use a `DataLoader`.
# 
# The `DataLoader` support multi-threading to optize your data-loading pipeline.

# In[ ]:


# Dataset Loader (Input Batcher)
batch_size = 100
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=batch_size, shuffle=False)


# #### Let's visualize some of the training samples

# In[ ]:


plt.figure(figsize=(16,9))
data, target = next(iter(train_loader))
for i in range(10):
    img = data.squeeze(1)[i]
    plt.subplot(1, 10, i+1)
    plt.imshow(img, cmap="gray", interpolation="none")
    plt.xlabel(target[i].item(), fontsize=18)
    plt.xticks([])
    plt.yticks([])


# ## Defining the model

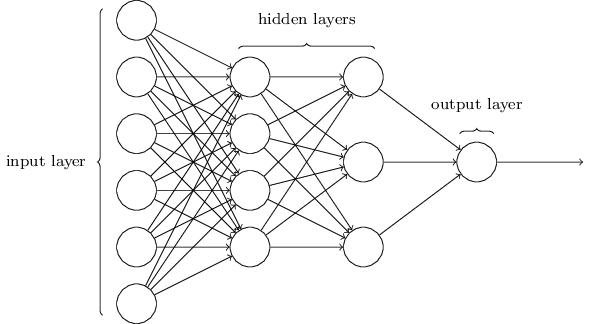
# A fully-connected neural network consists of layers that contain a number of values (neurons) computed as linear combinations of the neurons in the layer before. The first layer contains the network's input (your features), and the last layer contains the prediction. In our case, the last layer contains 10 neurons that are trained to be large when an input image is of the corresponding digit (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
# 
# The parameters of this model that are optimized (trained), are the weights that connect the neurons. These are drawn as edges in the illustration below.

# ![](https://raw.githubusercontent.com/ledell/sldm4-h2o/master/mlp_network.png)

# To make sure that neural networks can approximate non-linear functions, each neuron's value is transformed with some non-linear transformation function $\sigma(\cdot)$, often called an ‘activation function’ before being fed as input to the next layer. 
# 
# To be precise, the neurons $\vec x_{i+1}$ in layer $i+1$ are computed from the neurons $\vec x_i$ in layer $i$ as 
# 
# $$ \vec x_{i+1} = \sigma\left(W_{i+1} \vec x_i + \vec b_{i+1} \right) $$
# 
# where $W_{i+1}$ encodes the network parameters between each pair of input/output neurons in layer $i+1$, and $\vec b_{i+1}$ contains 'bias terms'. $\sigma$ operates element-wise.
# 
# A layer like that can be implemented using `torch.nn.Linear` followed by an activation function such as `torch.nn.ReLU` or `torch.nn.Sigmoid`.

# ---
# 
# __Exercise__<br>
# Implement a multi-layer fully-connected neural network with two hidden layers and the following numbers of neurons in each layer:
# 
# - Input-size: *input_size*
# - 1st hidden layer: 75
# - 2nd hidden layer: 50
# - Output layer: *num_classes*
# 
# Use `ReLU`s as ‘activation functions’ in between each pair of layers, but not after the last layer.

# In[ ]:


import torch.nn.functional as F  # provides some helper functions like Relu's, Sigmoids, Tanh, etc.

class MyNeuralNetwork(torch.nn.Module):
    def __init__(self, input_size, num_classes):
        super().__init__()
        
        self.input_size = input_size
        self.num_classes = num_classes
        
        self.linear_1 = torch.nn.Linear(input_size, 75)
        self.linear_2 = # YOUR TURN
        self.linear_3 = # YOUR TURN
        
    
    def forward(self, x):
        out = F.relu(self.linear_1(x))
        out = # YOUR TURN
        out = # YOUR TURN
        return out


# Now feed an input to your network:

# In[ ]:


x = torch.rand(16, 28 * 28)  # the first dimension is reserved for the 'batch_size'
model = MyNeuralNetwork(input_size=28 * 28, num_classes=10)
out = model(x)  # this calls model.forward(x)
out[0]


# __Exercise__ <br>
# What does `out[0, :]` above represent?

# ---

# ## Training the model
# 
# Most of the functions to train a model follow a similar pattern in PyTorch.
# In most of the cases in consists of the following steps:
# - Loop over data (in batches)
# - Create a prediction (forward pass)
# - Clear previous gradients (!)
# - Compute gradients (backward pass)
# - Parameter update (using an optimizer)

# In[ ]:


device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')


# Copy all model parameters to the GPU
model.to(device)


# Define the Loss function and Optimizer that you want to use
criterion = torch.nn.CrossEntropyLoss()  
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)  # NOTE: model.parameters()


# One epoch is a pass over the whole dataset
for epoch in range(5):
    total_loss = 0.0
    
    # Loop over batches in the training set
    for (inputs, labels) in train_loader:
        
        # Move inputs from CPU memory to GPU memory
        inputs = inputs.to(device)
        labels = labels.to(device)

        # The pixels in our images have a square 28x28 structure, but the network
        # accepts a *vector* of inputs. We therefore reshape it.
        # -1 is a special number that indicates 'whatever is left'
        # BS x 1 x 28 x 28 => BS x (28x28) 
        inputs = inputs.view(-1, 28*28)

        # Do a forward pass, loss computation, compute gradient, and optimize
        outputs = model(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()

        # Add up training losses so we can compute an average later
        total_loss += loss.item()
        
    print("Epoch %d, Loss=%.4f" % (epoch+1, total_loss/len(train_loader)))


# Note:
# - We can use the `.to` function on the model directly. Indeed, since PyTorch knows all the model parameters, it can put all the parameters on the correct device.
# - We use `model.parameters()` to get all the parameters of the model and we can instantiate an optimizer that will optimize these parameters `torch.optim.SGD(model.parameters())`.
# - To apply the forward function of the module, we write `model(input)`. In most cases, `model.forward(inputs)` would also work, but there is a slight difference : PyTorch allows you to register hook functions for a model that are automatically called when you do a forward pass on your model. Using `model(input)` will call these hooks and then call the forward function, while using `model.forward(inputs)` will just silently ignore them.
# 
# Do you see the convenience of Modules?

# ### Assessing model performance 
# This function loops over another `data_loader` (usually containing test/validation data) and computes the model's accuracy on it.

# In[ ]:


def accuracy(model, data_loader, device):
    with torch.no_grad(): # during model evaluation, we don't need the autograd mechanism (speeds things up)
        correct = 0
        total = 0
        for inputs, labels in data_loader:
            inputs = inputs.to(device)     
            inputs = inputs.view(-1, 28*28)
            
            outputs = model(inputs)
            _, predicted = outputs.max(1)
            
            correct += (predicted.cpu() == labels).sum().item()
            total += labels.size(0)
            
    acc = correct / total
    return acc


# In[ ]:


accuracy(model, train_loader, device)  # look at: accuracy(model, train_loader, device)


# In[ ]:


accuracy(model, test_loader, device)  # look at: accuracy(model, train_loader, device)


# ### We get an accuracy of around 97%. Can you improve this?

# ---

# ## Storing and loading models

# ### The easy way

# You can use `torch.load` and `torch.save` to load/save tensors and modules to disk.

# In[ ]:


torch.save(model, "my_model.pt")


# In[ ]:


my_model_loaded = torch.load("my_model.pt")


# In[ ]:


print(model.linear_3.bias)
print(my_model_loaded.linear_3.bias)


# ### The recommended way

# The recommended way is to save a dictionary containing all the parameters of the network.  
# To get this dictionary, you can use the `.state_dict()` function on the model.

# In[ ]:


torch.save(model.state_dict(), "my_model_state_dict.pt")


# In[ ]:


my_model_loaded = MyNeuralNetwork(28*28, 10)
my_model_loaded = model.load_state_dict(torch.load("my_model_state_dict"))


# In[ ]:


print(model.linear_3.bias)
print(my_model_loaded.linear_3.bias)


# ___
# 
# This intro to modules used [this medium post](https://medium.com/deeplearningbrasilia/deep-learning-introduction-to-pytorch-5bd39421c84) as a resource.

# <!--NAVIGATION-->
# # < [Optimization](4-Optimization.ipynb) | Modules | [CNN](6-CNN.ipynb) >