#!/usr/bin/env python
# coding: utf-8
# $$
# \newcommand{\mat}[1]{\boldsymbol {#1}}
# \newcommand{\mattr}[1]{\boldsymbol {#1}^\top}
# \newcommand{\matinv}[1]{\boldsymbol {#1}^{-1}}
# \newcommand{\vec}[1]{\boldsymbol {#1}}
# \newcommand{\vectr}[1]{\boldsymbol {#1}^\top}
# \newcommand{\rvar}[1]{\mathrm {#1}}
# \newcommand{\rvec}[1]{\boldsymbol{\mathrm{#1}}}
# \newcommand{\diag}{\mathop{\mathrm {diag}}}
# \newcommand{\set}[1]{\mathbb {#1}}
# \newcommand{\norm}[1]{\left\lVert#1\right\rVert}
# \newcommand{\pderiv}[2]{\frac{\partial #1}{\partial #2}}
# \newcommand{\bb}[1]{\boldsymbol{#1}}
# $$
#
#
# # CS236781: Deep Learning
# # Tutorial 3: Convolutional Neural Networks
# ## Introduction
#
# In this tutorial, we will cover:
#
# - Convolutional layers
# - Pooling layers
# - Network architecture
# - Spatial classification with fully-convolutional nets
# - Residual nets
# In[1]:
# Setup
get_ipython().run_line_magic('matplotlib', 'inline')
import os
import sys
import torch
import torchvision
import matplotlib.pyplot as plt
# In[2]:
plt.rcParams['font.size'] = 20
data_dir = os.path.expanduser('~/.pytorch-datasets')
# ## Theory Reminders
# ### Multilayer Perceptron (MLP)
# #### Model
#
#  # Composed of multiple **layers**.
#
# Each layer $j$ consists of $n_j$ regular perceptrons ("neurons") which calculate:
# $$
# \vec{y}_j = \varphi\left( \mat{W}_j \vec{y}_{j-1} + \vec{b}_j \right),~
# \mat{W}_j\in\set{R}^{n_{j}\times n_{j-1}},~ \vec{b}_j\in\set{R}^{n_j}.
# $$
#
# - Note that both input and output are **vectors**. We can think of the above equation as describing a layer of **multiple perceptrons**.
# - We'll henceforth refer to such layers as **fully-connected** or FC layers.
#
# Given an input sample $\vec{x}^i$, the computed function of an $L$-layer MLP is:
# $$
# \vec{y}_L^i= \varphi \left(
# \mat{W}_L \varphi \left( \cdots
# \varphi \left( \mat{W}_1 \vec{x}^i + \vec{b}_1 \right)
# \cdots \right)
# + \vec{b}_L \right)
# $$
# **Potent hypothesis class**: An MLP with $L>1$, can approximate virtually any continuous function given enough parameters (Cybenko, 1989).
# #### Limitations of MLPs for image classification
# Number of parameters increases quadratically with image size due to connectivity.
# - 28x28 MNIST image: 784 weights per neuron in the first layer
# - 1000x1000x3 color image: 3M weights **per neuron**
#
#
# Composed of multiple **layers**.
#
# Each layer $j$ consists of $n_j$ regular perceptrons ("neurons") which calculate:
# $$
# \vec{y}_j = \varphi\left( \mat{W}_j \vec{y}_{j-1} + \vec{b}_j \right),~
# \mat{W}_j\in\set{R}^{n_{j}\times n_{j-1}},~ \vec{b}_j\in\set{R}^{n_j}.
# $$
#
# - Note that both input and output are **vectors**. We can think of the above equation as describing a layer of **multiple perceptrons**.
# - We'll henceforth refer to such layers as **fully-connected** or FC layers.
#
# Given an input sample $\vec{x}^i$, the computed function of an $L$-layer MLP is:
# $$
# \vec{y}_L^i= \varphi \left(
# \mat{W}_L \varphi \left( \cdots
# \varphi \left( \mat{W}_1 \vec{x}^i + \vec{b}_1 \right)
# \cdots \right)
# + \vec{b}_L \right)
# $$
# **Potent hypothesis class**: An MLP with $L>1$, can approximate virtually any continuous function given enough parameters (Cybenko, 1989).
# #### Limitations of MLPs for image classification
# Number of parameters increases quadratically with image size due to connectivity.
# - 28x28 MNIST image: 784 weights per neuron in the first layer
# - 1000x1000x3 color image: 3M weights **per neuron**
#
#  # * Not enough compute
#
# * Overfitting
#
# Fully-connected layers are highly sensitivity to translation, while image features are inherently translation-invariant.
#
#
# * Not enough compute
#
# * Overfitting
#
# Fully-connected layers are highly sensitivity to translation, while image features are inherently translation-invariant.
#
#  # Despite all these limitations we still want to use deep neural nets because they allow us to learn hierarchical,
# non-linear transformations of the input.
# ## Convolutional Layers
# We'll explain how convolutional layers work in using three different "views", from the most non-formal to the most formal.
# ### Structural view
# Just for intuition, a convolutional layer **can be viewed** as a composition of neurons (as in an FC layer) but with three important distinctions.
# 1. The neurons can be thought of as stacked in a **3D** grid (insead of 1D).
# 1. Neurons that are at the same depth in the grid **share the same weights** (parameters $\mat{W},~\vec{b}$) (represented by color).
# 1. Each neuron is only **connected to a small region** of the previous layer's output (represented by location).
#
#
#
# Despite all these limitations we still want to use deep neural nets because they allow us to learn hierarchical,
# non-linear transformations of the input.
# ## Convolutional Layers
# We'll explain how convolutional layers work in using three different "views", from the most non-formal to the most formal.
# ### Structural view
# Just for intuition, a convolutional layer **can be viewed** as a composition of neurons (as in an FC layer) but with three important distinctions.
# 1. The neurons can be thought of as stacked in a **3D** grid (insead of 1D).
# 1. Neurons that are at the same depth in the grid **share the same weights** (parameters $\mat{W},~\vec{b}$) (represented by color).
# 1. Each neuron is only **connected to a small region** of the previous layer's output (represented by location).
#
#
#  # Crucially, each neuron is spatially local, but operates on the **full depth** dimension of its input layer.
#
#
# Crucially, each neuron is spatially local, but operates on the **full depth** dimension of its input layer.
#
#  # ### Filter-based view
# Since each neuron in a given depth-slice of operates on a small region of the input layer, we can think of the combined **output of that depth-slice** as a **filtered version of the input volume**.
#
#
# ### Filter-based view
# Since each neuron in a given depth-slice of operates on a small region of the input layer, we can think of the combined **output of that depth-slice** as a **filtered version of the input volume**.
#
#  # Imagine sliding the filter along the input and computing an inner product at each point.
#
#
# Imagine sliding the filter along the input and computing an inner product at each point.
#
#  #
# Since we have multiple depth-slices per convolutional layer, the layer computes multiple convolutions of the same input with different kernels (filters).
#
# Each 2D slice of an input and output volume is known as **feature map** or a **channel**.
# ### Formal definitions
# Given an input tensor $\vec{x}$ of shape $(C_{\text{in}}, H_{\text{in}}, W_{\text{in}})$,
# a convolutional layer produces an output tensor $\vec{y}$ of shape $(C_{\text{out}}, H_{\text{out}}, W_{\text{out}})$,
# such that:
# $$
# \vec{y}^j = \sum_{i=1}^{C_\text{in}} \vec{w}^{ij}\ast\vec{x}^i+b^j;\ j=1,2,\dots,C_\text{out}
# $$
# is the $j$-th feature map (or channel) of the output tensor $\vec{y}$, the $\ast$ denotes convolution, and $x^i$ is the $i$-th input feature map.
# Recall the definition of the convolution operator:
# $$
# \left\{\vec{g}\ast\vec{f}\right\}_j = \sum_{i} g_{j-i} f_{i}.
# $$
#
#
#
# Since we have multiple depth-slices per convolutional layer, the layer computes multiple convolutions of the same input with different kernels (filters).
#
# Each 2D slice of an input and output volume is known as **feature map** or a **channel**.
# ### Formal definitions
# Given an input tensor $\vec{x}$ of shape $(C_{\text{in}}, H_{\text{in}}, W_{\text{in}})$,
# a convolutional layer produces an output tensor $\vec{y}$ of shape $(C_{\text{out}}, H_{\text{out}}, W_{\text{out}})$,
# such that:
# $$
# \vec{y}^j = \sum_{i=1}^{C_\text{in}} \vec{w}^{ij}\ast\vec{x}^i+b^j;\ j=1,2,\dots,C_\text{out}
# $$
# is the $j$-th feature map (or channel) of the output tensor $\vec{y}$, the $\ast$ denotes convolution, and $x^i$ is the $i$-th input feature map.
# Recall the definition of the convolution operator:
# $$
# \left\{\vec{g}\ast\vec{f}\right\}_j = \sum_{i} g_{j-i} f_{i}.
# $$
#
#  #
# Note that in practice, correlation is used instead of convolution, as there's no need to "flip" a learned filter.
# Convolution is a **linear** and **shift-equivariant** operator.
# Linear means it can be represented simply as a matrix multiplication.
#
# Shift-equivariance means that a shifted input will result in an output shifted by the same amount.
# Due to this property, the matrix representing a convolution is always a **Toeplitz** matrix.
#
#
#
# Note that in practice, correlation is used instead of convolution, as there's no need to "flip" a learned filter.
# Convolution is a **linear** and **shift-equivariant** operator.
# Linear means it can be represented simply as a matrix multiplication.
#
# Shift-equivariance means that a shifted input will result in an output shifted by the same amount.
# Due to this property, the matrix representing a convolution is always a **Toeplitz** matrix.
#
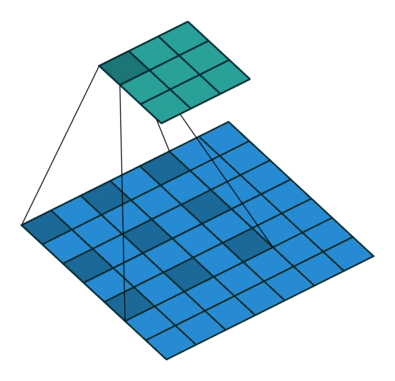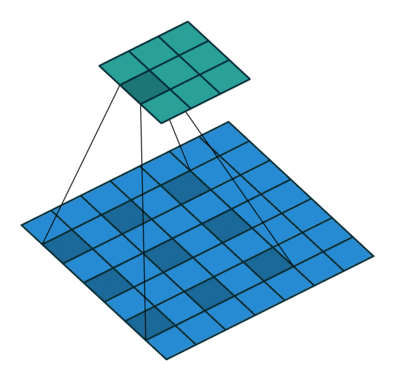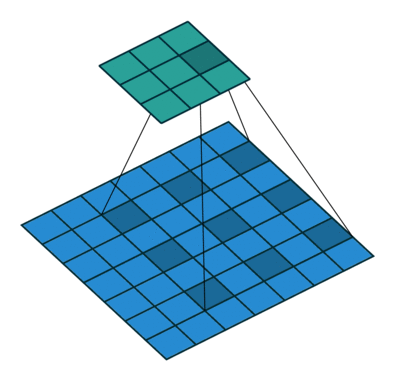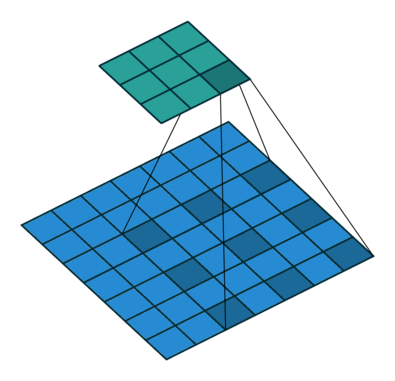
#  # ### Hyperparameters & dimentions
#
# Assume an input volume of shape $(C_{\mathrm{in}}, H_{\mathrm{in}}, W_{\mathrm{in}})$, i.e. channels, height, width.
# Define,
#
# 1. Number of kernels, $K \geq 1$.
# 2. Spatial extent (size) of each kernel, $F \geq 1$.
# 3. Stride $S\geq 1$: spatial distance between consecutive applications of a kernel.
# 4. Padding $P\geq 0$: Number of "pixels" to zero-pad around each input feature map.
# 5. Dilation $D \geq 1$: Spacing between kernel elements when applying to input.
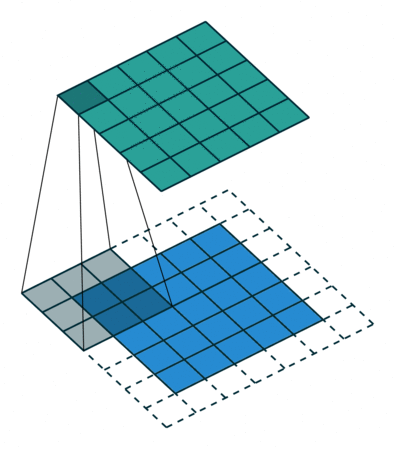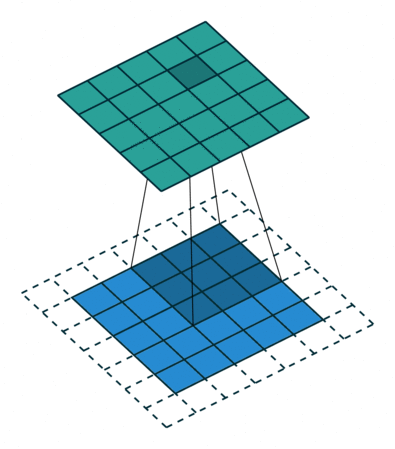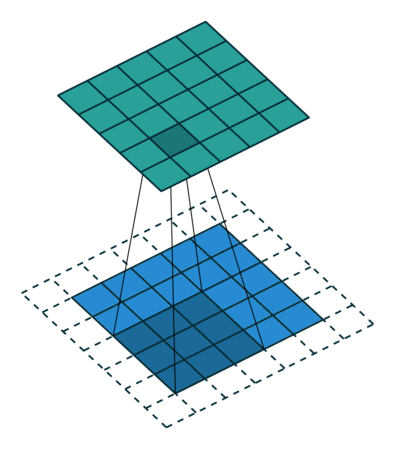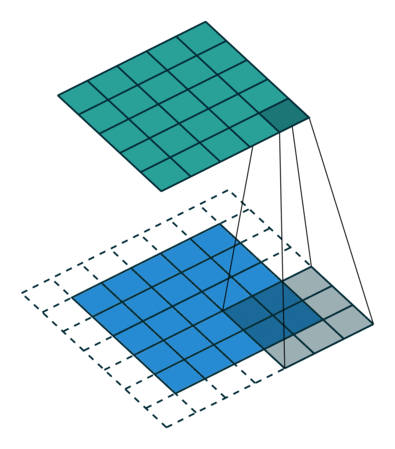
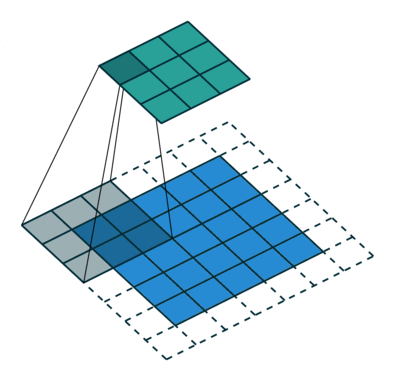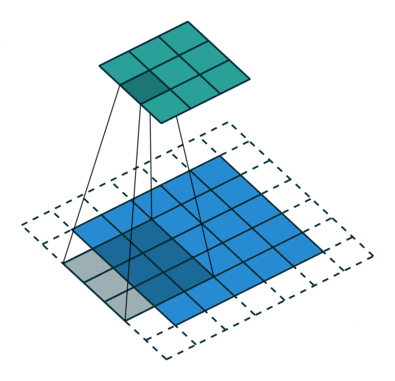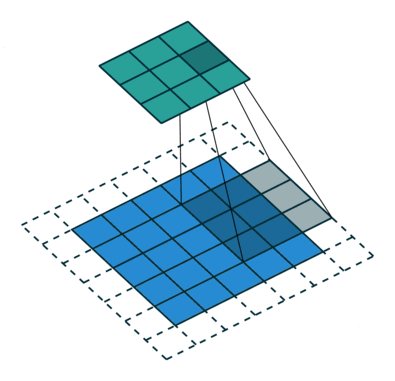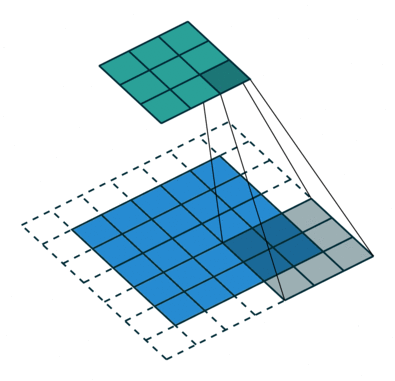
# In the following animations, **blue** maps are inputs,
# **green** maps are outputs and
# the **shaded** area is the kernel with $F=3$.
#
# | $P=0,~S=1,~D=1$ | $P=1,~S=1,~D=1$ | $P=1,~S=2,~D=1$ | $P=0,~S=1,~D=2$ |
# |-----------------|-----------------|-----------------| --------------- |
# |
# ### Hyperparameters & dimentions
#
# Assume an input volume of shape $(C_{\mathrm{in}}, H_{\mathrm{in}}, W_{\mathrm{in}})$, i.e. channels, height, width.
# Define,
#
# 1. Number of kernels, $K \geq 1$.
# 2. Spatial extent (size) of each kernel, $F \geq 1$.
# 3. Stride $S\geq 1$: spatial distance between consecutive applications of a kernel.
# 4. Padding $P\geq 0$: Number of "pixels" to zero-pad around each input feature map.
# 5. Dilation $D \geq 1$: Spacing between kernel elements when applying to input.
# In the following animations, **blue** maps are inputs,
# **green** maps are outputs and
# the **shaded** area is the kernel with $F=3$.
#
# | $P=0,~S=1,~D=1$ | $P=1,~S=1,~D=1$ | $P=1,~S=2,~D=1$ | $P=0,~S=1,~D=2$ |
# |-----------------|-----------------|-----------------| --------------- |
# |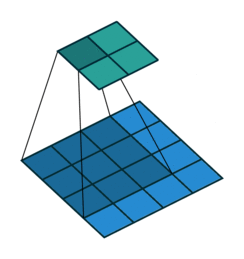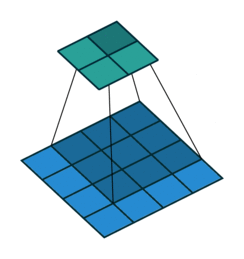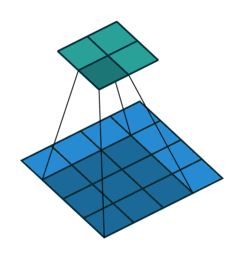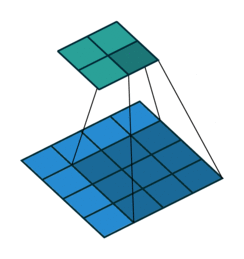 |
|  |
|  |
|  |
#
#
# We can see that the second combination, $F=3,~P=1,~S=1,~D=1$, leads to identical sizes of input and output feature maps.
# A 3D view
#
# | $P=0,~S=1,~D=1$ | $P=1,~S=1,~D=1$ | $P=1,~S=2,~D=1$ |
# |-----------------|-----------------|-----------------|
# |
|
#
#
# We can see that the second combination, $F=3,~P=1,~S=1,~D=1$, leads to identical sizes of input and output feature maps.
# A 3D view
#
# | $P=0,~S=1,~D=1$ | $P=1,~S=1,~D=1$ | $P=1,~S=2,~D=1$ |
# |-----------------|-----------------|-----------------|
# | |
|  |
|  |
#
#
# Then, given a set of hyperparameters,
#
# - Each convolution kernel will (usually) be a tensor of shape $(C_{\mathrm{in}}, F, F)$.
# - The ouput volume dimensions will be:
#
# $$\begin{align}
# H_{\mathrm{out}} &= \left\lfloor \frac{H_{\mathrm{in}} + 2P - D\cdot(F-1) -1}{S} \right\rfloor + 1\\
# W_{\mathrm{out}} &= \left\lfloor \frac{W_{\mathrm{in}} + 2P - D\cdot(F-1) -1}{S} \right\rfloor + 1\\
# C_{\mathrm{out}} &= K\\
# \end{align}$$
# - The number of parameters in a convolutional **layer** will be:
# $$
# \underbrace{K}_{\mathrm{kernels}} \cdot \left(
# \underbrace{C_{\mathrm{in}} \cdot F^2}_{\mathrm{kernel\ parameters}} + \underbrace{1}_{\mathrm{bias\ term}}
# \right)
# $$
# **Example**: Input image is 1000x1000x3, and the first conv layer has $10$ kernels of size 5x5.
# The number of parameters in the first layer will be: $ 10 \cdot 3 \cdot 5^2 + 10 = 760 $.
#
# ### Pytorch `Conv2d` layer example
# In[3]:
import torchvision.transforms as tvtf
tf = tvtf.Compose([tvtf.ToTensor()])
ds_cifar10 = torchvision.datasets.CIFAR10(data_dir, download=True, train=True, transform=tf)
# In[4]:
# Load first CIFAR10 image
x0,y0 = ds_cifar10[0]
# add batch dimension
x0 = x0.unsqueeze(0)
# Note: channels come before spatial extent
print('x0 shape with batch dim:', x0.shape)
# In[5]:
# A function to count the number of parameters in an nn.Module.
def num_params(layer):
return sum([p.numel() for p in layer.parameters()])
# Let's create our first conv layer with pytorch:
# In[7]:
import torch.nn as nn
# First conv layer: works on input image volume
conv1 = nn.Conv2d(in_channels=x0.shape[1], out_channels=10, padding=1, kernel_size=5, stride=1,dialation=1)
print(f'conv1: {num_params(conv1)} parameters')
# Number of parameters: $10\cdot(3\cdot3^2+1)=280$
# In[8]:
# Apply the layer to an input
print(f'{"Input image shape:":25s}{x0.shape}')
y1 = conv1(x0)
print(f'{"After first conv layer:":25s}{y1.shape}')
# In[9]:
# Second conv layer: works on output volume of first layer
conv2 = nn.Conv2d(in_channels=10, out_channels=20, padding=0, kernel_size=7, stride=2)
print(f'conv2: {num_params(conv2)} parameters')
y2 = conv2(conv1(x0))
print(f'{"After second conv layer:":25s}{y2.shape}')
# New spatial extent:
#
# $$
# H_{\mathrm{out}} = \left\lfloor \frac{H_{\mathrm{in}} + 2P -F}{S} \right\rfloor + 1
# =
# \left\lfloor \frac{32 + 2\cdot 0 -6}{2} \right\rfloor + 1
# =
# 14
# $$
#
# **Note**: observe that the width and height dimensions of the input image were never specified!
# more on the significance of that later.
# ## Pooling layers
# In addition to strides, another way to reduce the size of feature maps between the convolutional layers,
# is by adding **pooling** layers.
# A pooling layer has the following hyperparameters (but **no trainable parameters**):
#
# 1. Spatial extent (size) of each pooling kernel, $F \geq 2$.
# 1. Stride $S\geq 2$: spatial distance between consecutive applications.
# 1. Operation (e.g. max, average, $p$-norm)
#
# **Example**: $\max$-pooling with $F=2,~S=2$ performing a factor-2 downsample:
#
#
|
#
#
# Then, given a set of hyperparameters,
#
# - Each convolution kernel will (usually) be a tensor of shape $(C_{\mathrm{in}}, F, F)$.
# - The ouput volume dimensions will be:
#
# $$\begin{align}
# H_{\mathrm{out}} &= \left\lfloor \frac{H_{\mathrm{in}} + 2P - D\cdot(F-1) -1}{S} \right\rfloor + 1\\
# W_{\mathrm{out}} &= \left\lfloor \frac{W_{\mathrm{in}} + 2P - D\cdot(F-1) -1}{S} \right\rfloor + 1\\
# C_{\mathrm{out}} &= K\\
# \end{align}$$
# - The number of parameters in a convolutional **layer** will be:
# $$
# \underbrace{K}_{\mathrm{kernels}} \cdot \left(
# \underbrace{C_{\mathrm{in}} \cdot F^2}_{\mathrm{kernel\ parameters}} + \underbrace{1}_{\mathrm{bias\ term}}
# \right)
# $$
# **Example**: Input image is 1000x1000x3, and the first conv layer has $10$ kernels of size 5x5.
# The number of parameters in the first layer will be: $ 10 \cdot 3 \cdot 5^2 + 10 = 760 $.
#
# ### Pytorch `Conv2d` layer example
# In[3]:
import torchvision.transforms as tvtf
tf = tvtf.Compose([tvtf.ToTensor()])
ds_cifar10 = torchvision.datasets.CIFAR10(data_dir, download=True, train=True, transform=tf)
# In[4]:
# Load first CIFAR10 image
x0,y0 = ds_cifar10[0]
# add batch dimension
x0 = x0.unsqueeze(0)
# Note: channels come before spatial extent
print('x0 shape with batch dim:', x0.shape)
# In[5]:
# A function to count the number of parameters in an nn.Module.
def num_params(layer):
return sum([p.numel() for p in layer.parameters()])
# Let's create our first conv layer with pytorch:
# In[7]:
import torch.nn as nn
# First conv layer: works on input image volume
conv1 = nn.Conv2d(in_channels=x0.shape[1], out_channels=10, padding=1, kernel_size=5, stride=1,dialation=1)
print(f'conv1: {num_params(conv1)} parameters')
# Number of parameters: $10\cdot(3\cdot3^2+1)=280$
# In[8]:
# Apply the layer to an input
print(f'{"Input image shape:":25s}{x0.shape}')
y1 = conv1(x0)
print(f'{"After first conv layer:":25s}{y1.shape}')
# In[9]:
# Second conv layer: works on output volume of first layer
conv2 = nn.Conv2d(in_channels=10, out_channels=20, padding=0, kernel_size=7, stride=2)
print(f'conv2: {num_params(conv2)} parameters')
y2 = conv2(conv1(x0))
print(f'{"After second conv layer:":25s}{y2.shape}')
# New spatial extent:
#
# $$
# H_{\mathrm{out}} = \left\lfloor \frac{H_{\mathrm{in}} + 2P -F}{S} \right\rfloor + 1
# =
# \left\lfloor \frac{32 + 2\cdot 0 -6}{2} \right\rfloor + 1
# =
# 14
# $$
#
# **Note**: observe that the width and height dimensions of the input image were never specified!
# more on the significance of that later.
# ## Pooling layers
# In addition to strides, another way to reduce the size of feature maps between the convolutional layers,
# is by adding **pooling** layers.
# A pooling layer has the following hyperparameters (but **no trainable parameters**):
#
# 1. Spatial extent (size) of each pooling kernel, $F \geq 2$.
# 1. Stride $S\geq 2$: spatial distance between consecutive applications.
# 1. Operation (e.g. max, average, $p$-norm)
#
# **Example**: $\max$-pooling with $F=2,~S=2$ performing a factor-2 downsample:
#
#  # ### Why pool feature maps after convolutions?
# One reason is to more rapidly increase the **receptive field** of each layer.
#
#
# ### Why pool feature maps after convolutions?
# One reason is to more rapidly increase the **receptive field** of each layer.
#
#  # - Receptive field size increases more rapidly if we add pooling, strides or dilation.
# - We want successive conv layers to be affected by increasingly larger parts of the input image.
# - This allows us to learn a hierarchy of visual features.
#
#
# - Receptive field size increases more rapidly if we add pooling, strides or dilation.
# - We want successive conv layers to be affected by increasingly larger parts of the input image.
# - This allows us to learn a hierarchy of visual features.
#
#  # Another reason is to add **invariance** to changes in the input.
#
# - Pooling within feature maps: introduces invariance to small translations
#
# Another reason is to add **invariance** to changes in the input.
#
# - Pooling within feature maps: introduces invariance to small translations
#  # - Pooling across feature maps: introduces invariance to learned transformations
#
# - Pooling across feature maps: introduces invariance to learned transformations
#  # ### PyTorch `Pool2d` layer example
# In[10]:
pool = nn.MaxPool2d(kernel_size=2, stride=2)
print(f'{"After second conv layer:":25s}{conv2(conv1(x0)).shape}')
print(f'{"After max-pool:":25s}{pool(conv2(conv1(x0))).shape}')
# ## Network Architecture
# The basic way to build an architecture of a deep convolutional neural net, is to repeat groups of **conv-relu** layers, optionally add **pooling** in between and end with an **FC-softmax** combination.
#
#
# Why does such a scheme make sense, e.g. for image classification?
#
# ### PyTorch `Pool2d` layer example
# In[10]:
pool = nn.MaxPool2d(kernel_size=2, stride=2)
print(f'{"After second conv layer:":25s}{conv2(conv1(x0)).shape}')
print(f'{"After max-pool:":25s}{pool(conv2(conv1(x0))).shape}')
# ## Network Architecture
# The basic way to build an architecture of a deep convolutional neural net, is to repeat groups of **conv-relu** layers, optionally add **pooling** in between and end with an **FC-softmax** combination.
#
#
# Why does such a scheme make sense, e.g. for image classification?
#  # In the above image,
#
# - all the **conv** blocks shown are actually **conv-relu** (or some other nonlinearity).
# - The repeating **conv-conv-...-pool** blocks are learned, non-linear feature extractors: they learn to detect specific features in an image (e.g. lines at different orientations).
# - The pooling controls the receptive field increase, so that more high-level features can be generated by each conv group (e.g. shapes composed from multiple simple lines).
# - The **FC-softmax** at the end is just an MLP that uses the extracted features for classification.
# - Training end-to-end learns the classifier together with the features!
# - The rightmost architecture is called VGG, and used to be a relevant architecture for ImageNet classification.
# - Other types of layers, such as normalization layers are usually also added.
# There are many other things to consider as part of the architecture:
# - Size of conv kernels
# - Number of consecutive convolutions
# - Use of batch normalization to speed up training
# - Dropout for improved generalization
# - Not using FC layers (we'll see later)
# - Skip connections (we'll see later)
#
# All of these could be hyperparameters to cross-validate over!
# Many different network architectures exist, made famous mainly by repeated improvements on the ImageNet classification challenge since 2012.
#
#
# In the above image,
#
# - all the **conv** blocks shown are actually **conv-relu** (or some other nonlinearity).
# - The repeating **conv-conv-...-pool** blocks are learned, non-linear feature extractors: they learn to detect specific features in an image (e.g. lines at different orientations).
# - The pooling controls the receptive field increase, so that more high-level features can be generated by each conv group (e.g. shapes composed from multiple simple lines).
# - The **FC-softmax** at the end is just an MLP that uses the extracted features for classification.
# - Training end-to-end learns the classifier together with the features!
# - The rightmost architecture is called VGG, and used to be a relevant architecture for ImageNet classification.
# - Other types of layers, such as normalization layers are usually also added.
# There are many other things to consider as part of the architecture:
# - Size of conv kernels
# - Number of consecutive convolutions
# - Use of batch normalization to speed up training
# - Dropout for improved generalization
# - Not using FC layers (we'll see later)
# - Skip connections (we'll see later)
#
# All of these could be hyperparameters to cross-validate over!
# Many different network architectures exist, made famous mainly by repeated improvements on the ImageNet classification challenge since 2012.
#
#  # Notable ImageNet-winning architectures:
#
# - AlexNet, 5 layers (2012): Based on LeNet, deeper, with ReLU, trained with GPUs
# - Inception/GoogLeNet, 22 layers (2014): Multiple (small) kernel sizes at same depth
# - ResNet, 152 (!) layers (2015): Skip connections
# ### What filters are deep CNNs learning?
# CNNs capture hierarchical features, with deeper layers capturing higher-level, class-specific features
# (Zeiler & Fergus, 2013).
#
#
# Notable ImageNet-winning architectures:
#
# - AlexNet, 5 layers (2012): Based on LeNet, deeper, with ReLU, trained with GPUs
# - Inception/GoogLeNet, 22 layers (2014): Multiple (small) kernel sizes at same depth
# - ResNet, 152 (!) layers (2015): Skip connections
# ### What filters are deep CNNs learning?
# CNNs capture hierarchical features, with deeper layers capturing higher-level, class-specific features
# (Zeiler & Fergus, 2013).
#
#  # This visualization shows patterns which maximally-activate kernels at various layers of a conv net.
# ### PyTorch network architecture example
# Let's implement **LeNet**, arguably the first successful CNN model for MNIST (LeCun, 1998).
#
#
# This visualization shows patterns which maximally-activate kernels at various layers of a conv net.
# ### PyTorch network architecture example
# Let's implement **LeNet**, arguably the first successful CNN model for MNIST (LeCun, 1998).
#
# 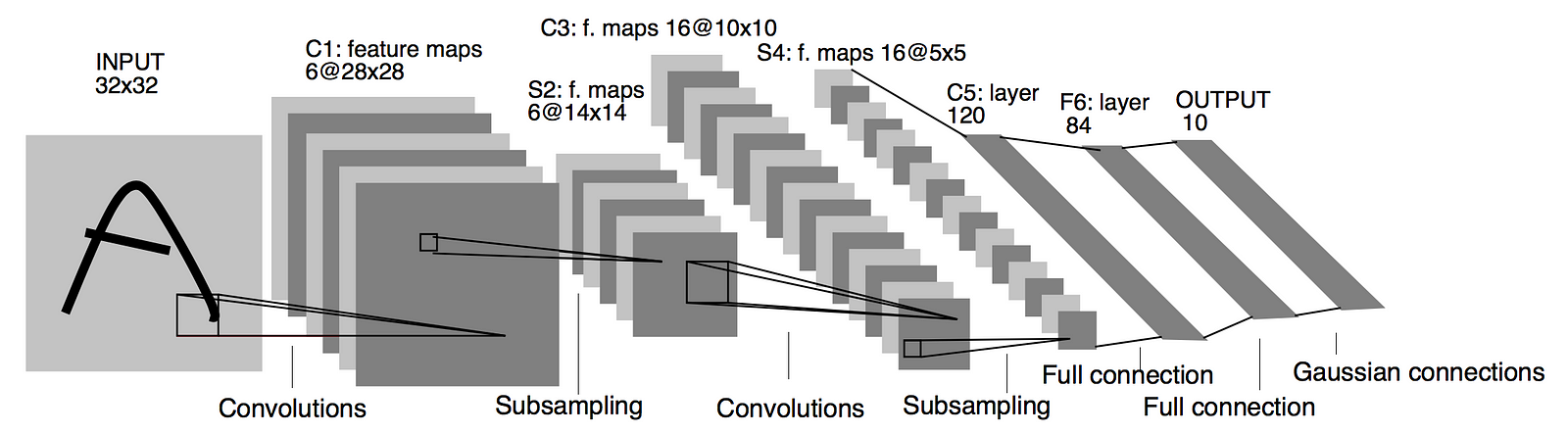 # In[11]:
class LeNet(nn.Module):
def __init__(self, in_channels=3):
super().__init__()
self.feature_extractor = nn.Sequential(
nn.Conv2d(in_channels, out_channels=6, kernel_size=5),
nn.ReLU(),
nn.MaxPool2d(2),
nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),
nn.ReLU(),
nn.MaxPool2d(2),
)
self.classifier = nn.Sequential(
nn.Linear(16*5*5, 120), # Why 16*5*5 ?
nn.ReLU(),
nn.Linear(120, 84), # (N, 120) -> (N, 84)
nn.ReLU(),
nn.Linear(84, 10) # (N, 84) -> (N, 10)
)
def forward(self, x):
features = self.feature_extractor(x)
features = features.view(features.size(0), -1)
class_scores = self.classifier(features)
return class_scores
# In[12]:
net = LeNet()
print(net)
# In[13]:
# Test forward pass
print('x0 shape=', x0.shape, end='\n\n')
print('LeNet(x0)=', net(x0), end='\n\n')
print('shape=', net(x0).shape)
# ### Fully-convolutional Networks
# you can read at home, not for the homework
# Notice how we never actually specified the input image size when implementing the network.
#
# **Does this mean we can use the network on images of any size**?
# **No**, because of the FC layers at the end.
#
# Here, let's try:
# In[14]:
large_image = torch.randn(1,3,32*2,32*2)
try:
net(large_image)
except RuntimeError as e:
print(e, file=sys.stderr)
# However: Only the FC layers at the end require actual knowledge of exact image sizes.
# We can replace them with... More convolutions, of course
# What would we get from:
#
# - Kernels of size 1x1?
# - Kernels of size HxW (full spatial extent)?
#
#
#
# In[11]:
class LeNet(nn.Module):
def __init__(self, in_channels=3):
super().__init__()
self.feature_extractor = nn.Sequential(
nn.Conv2d(in_channels, out_channels=6, kernel_size=5),
nn.ReLU(),
nn.MaxPool2d(2),
nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5),
nn.ReLU(),
nn.MaxPool2d(2),
)
self.classifier = nn.Sequential(
nn.Linear(16*5*5, 120), # Why 16*5*5 ?
nn.ReLU(),
nn.Linear(120, 84), # (N, 120) -> (N, 84)
nn.ReLU(),
nn.Linear(84, 10) # (N, 84) -> (N, 10)
)
def forward(self, x):
features = self.feature_extractor(x)
features = features.view(features.size(0), -1)
class_scores = self.classifier(features)
return class_scores
# In[12]:
net = LeNet()
print(net)
# In[13]:
# Test forward pass
print('x0 shape=', x0.shape, end='\n\n')
print('LeNet(x0)=', net(x0), end='\n\n')
print('shape=', net(x0).shape)
# ### Fully-convolutional Networks
# you can read at home, not for the homework
# Notice how we never actually specified the input image size when implementing the network.
#
# **Does this mean we can use the network on images of any size**?
# **No**, because of the FC layers at the end.
#
# Here, let's try:
# In[14]:
large_image = torch.randn(1,3,32*2,32*2)
try:
net(large_image)
except RuntimeError as e:
print(e, file=sys.stderr)
# However: Only the FC layers at the end require actual knowledge of exact image sizes.
# We can replace them with... More convolutions, of course
# What would we get from:
#
# - Kernels of size 1x1?
# - Kernels of size HxW (full spatial extent)?
#
#
#  # Lets create a fully-convolutional LeNet:
# In[15]:
class LeNetFullyConv(LeNet):
def __init__(self):
super().__init__()
# Remember: the last feature map volume has shape (16,5,5) for the original image size
# Override the classifier with 5x5 then 1x1 convolutions
# Try to figure out the output shape after each of the following convolutions:
self.classifier = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5), # no padding or strides!
nn.ReLU(),
nn.Conv2d(in_channels=120, out_channels=84, kernel_size=1), # 1x1 conv
nn.ReLU(),
nn.Conv2d(in_channels=84, out_channels=10, kernel_size=1), # 1x1 conv
)
def forward(self, x):
# Using feature extractor block from the base model
features = self.feature_extractor(x)
# note: no need to reshape the features now
class_scores = self.classifier(features)
return class_scores
# In[16]:
net_fully_conv = LeNetFullyConv()
print(net_fully_conv)
# Let's forward the original-sized image and the larger image through the network and observe the output shapes:
# In[17]:
print('regular image output shape:', net_fully_conv(x0).shape)
print('large image output shape:', net_fully_conv(large_image).shape)
# **What's the meaning of the output after conversion to fully convolutional?**
# It's now a **spatial classification map**.
#
#
# Lets create a fully-convolutional LeNet:
# In[15]:
class LeNetFullyConv(LeNet):
def __init__(self):
super().__init__()
# Remember: the last feature map volume has shape (16,5,5) for the original image size
# Override the classifier with 5x5 then 1x1 convolutions
# Try to figure out the output shape after each of the following convolutions:
self.classifier = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=120, kernel_size=5), # no padding or strides!
nn.ReLU(),
nn.Conv2d(in_channels=120, out_channels=84, kernel_size=1), # 1x1 conv
nn.ReLU(),
nn.Conv2d(in_channels=84, out_channels=10, kernel_size=1), # 1x1 conv
)
def forward(self, x):
# Using feature extractor block from the base model
features = self.feature_extractor(x)
# note: no need to reshape the features now
class_scores = self.classifier(features)
return class_scores
# In[16]:
net_fully_conv = LeNetFullyConv()
print(net_fully_conv)
# Let's forward the original-sized image and the larger image through the network and observe the output shapes:
# In[17]:
print('regular image output shape:', net_fully_conv(x0).shape)
print('large image output shape:', net_fully_conv(large_image).shape)
# **What's the meaning of the output after conversion to fully convolutional?**
# It's now a **spatial classification map**.
#
#  #
# ## Residual Networks
#
#
# ## Residual Networks
#  #
# For image-related tasks it seems that **deeper is better**: learn more complex features.
#
# How deep can we go? Should more depth always improve results?
# In theory, adding an addition layer should provide **at least** the same accuracy as before.
# Extra layers could always be just identity maps.
#
# In practice, there are two major problems with adding depth:
# 1. More difficult convergence: vanishing gradients
# 1. More difficult optimization: parameter space increases
#
#
# For image-related tasks it seems that **deeper is better**: learn more complex features.
#
# How deep can we go? Should more depth always improve results?
# In theory, adding an addition layer should provide **at least** the same accuracy as before.
# Extra layers could always be just identity maps.
#
# In practice, there are two major problems with adding depth:
# 1. More difficult convergence: vanishing gradients
# 1. More difficult optimization: parameter space increases
#  #
# I.e., even if the same solution (or better) exists, SGD-based optimization can't find it. **Optimization error** increased with depth.
# ResNets attempt to address these issues by building a network architecture composed of convolutional blocks with added **shortcut-connections**:
#
#
#
# I.e., even if the same solution (or better) exists, SGD-based optimization can't find it. **Optimization error** increased with depth.
# ResNets attempt to address these issues by building a network architecture composed of convolutional blocks with added **shortcut-connections**:
#
#  #
# (Left: basic block; right: bottleneck block).
#
# Here the weight layers are `3x3` or `1x1` convolutions followed by batch-normalization.
#
# **Why do these shortcut-connections help?**
# These shortcuts create two key advantages:
# - Allow gradients to "flow" freely backwards
# - Each block only learns the "residual mapping", i.e. some delta from the identity map which is easier to optimize.
# Implementation: In the homeworks :)
# #### Thanks!
# **Credits**
#
# This tutorial was written by [Aviv A. Rosenberg](https://avivr.net) and [Moshe Kimhi](https://mkimhi.github.io/).
#
# (Left: basic block; right: bottleneck block).
#
# Here the weight layers are `3x3` or `1x1` convolutions followed by batch-normalization.
#
# **Why do these shortcut-connections help?**
# These shortcuts create two key advantages:
# - Allow gradients to "flow" freely backwards
# - Each block only learns the "residual mapping", i.e. some delta from the identity map which is easier to optimize.
# Implementation: In the homeworks :)
# #### Thanks!
# **Credits**
#
# This tutorial was written by [Aviv A. Rosenberg](https://avivr.net) and [Moshe Kimhi](https://mkimhi.github.io/).
# To re-use, please provide attribution and link to the original.
#
# Some images in this tutorial were taken and/or adapted from the following sources:
#
# - Sebastian Raschka, https://sebastianraschka.com/
# - Deep Learning, Goodfellow, Bengio and Courville, MIT Press, 2016
# - Fundamentals of Deep Learning, Nikhil Buduma, Oreilly 2017
# - Deep Learning with Python, Francios Chollet, Manning 2018
# - Stanford cs231n course notes by Andrej Karpathy
# - https://github.com/vdumoulin/conv_arithmetic
# - Long, J., Shelhamer, E., & Darrell, T. (2015). Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition.
# - Canziani, A., Paszke, A., & Culurciello, E. (2016). An analysis of deep neural network models for practical applications.
# - He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition.
# - A Comprehensive Introduction to Different Types of Convolutions in Deep Learning, Kulun Bai
# - https://animatedai.github.io/
# In[ ]:










 |
|  |
|  |
|  |
#
#
# We can see that the second combination, $F=3,~P=1,~S=1,~D=1$, leads to identical sizes of input and output feature maps.
# A 3D view
#
# | $P=0,~S=1,~D=1$ | $P=1,~S=1,~D=1$ | $P=1,~S=2,~D=1$ |
# |-----------------|-----------------|-----------------|
# |
|
#
#
# We can see that the second combination, $F=3,~P=1,~S=1,~D=1$, leads to identical sizes of input and output feature maps.
# A 3D view
#
# | $P=0,~S=1,~D=1$ | $P=1,~S=1,~D=1$ | $P=1,~S=2,~D=1$ |
# |-----------------|-----------------|-----------------|
# | |
|  |
|  |
#
#
# Then, given a set of hyperparameters,
#
# - Each convolution kernel will (usually) be a tensor of shape $(C_{\mathrm{in}}, F, F)$.
# - The ouput volume dimensions will be:
#
# $$\begin{align}
# H_{\mathrm{out}} &= \left\lfloor \frac{H_{\mathrm{in}} + 2P - D\cdot(F-1) -1}{S} \right\rfloor + 1\\
# W_{\mathrm{out}} &= \left\lfloor \frac{W_{\mathrm{in}} + 2P - D\cdot(F-1) -1}{S} \right\rfloor + 1\\
# C_{\mathrm{out}} &= K\\
# \end{align}$$
# - The number of parameters in a convolutional **layer** will be:
# $$
# \underbrace{K}_{\mathrm{kernels}} \cdot \left(
# \underbrace{C_{\mathrm{in}} \cdot F^2}_{\mathrm{kernel\ parameters}} + \underbrace{1}_{\mathrm{bias\ term}}
# \right)
# $$
# **Example**: Input image is 1000x1000x3, and the first conv layer has $10$ kernels of size 5x5.
# The number of parameters in the first layer will be: $ 10 \cdot 3 \cdot 5^2 + 10 = 760 $.
#
# ### Pytorch `Conv2d` layer example
# In[3]:
import torchvision.transforms as tvtf
tf = tvtf.Compose([tvtf.ToTensor()])
ds_cifar10 = torchvision.datasets.CIFAR10(data_dir, download=True, train=True, transform=tf)
# In[4]:
# Load first CIFAR10 image
x0,y0 = ds_cifar10[0]
# add batch dimension
x0 = x0.unsqueeze(0)
# Note: channels come before spatial extent
print('x0 shape with batch dim:', x0.shape)
# In[5]:
# A function to count the number of parameters in an nn.Module.
def num_params(layer):
return sum([p.numel() for p in layer.parameters()])
# Let's create our first conv layer with pytorch:
# In[7]:
import torch.nn as nn
# First conv layer: works on input image volume
conv1 = nn.Conv2d(in_channels=x0.shape[1], out_channels=10, padding=1, kernel_size=5, stride=1,dialation=1)
print(f'conv1: {num_params(conv1)} parameters')
# Number of parameters: $10\cdot(3\cdot3^2+1)=280$
# In[8]:
# Apply the layer to an input
print(f'{"Input image shape:":25s}{x0.shape}')
y1 = conv1(x0)
print(f'{"After first conv layer:":25s}{y1.shape}')
# In[9]:
# Second conv layer: works on output volume of first layer
conv2 = nn.Conv2d(in_channels=10, out_channels=20, padding=0, kernel_size=7, stride=2)
print(f'conv2: {num_params(conv2)} parameters')
y2 = conv2(conv1(x0))
print(f'{"After second conv layer:":25s}{y2.shape}')
# New spatial extent:
#
# $$
# H_{\mathrm{out}} = \left\lfloor \frac{H_{\mathrm{in}} + 2P -F}{S} \right\rfloor + 1
# =
# \left\lfloor \frac{32 + 2\cdot 0 -6}{2} \right\rfloor + 1
# =
# 14
# $$
#
# **Note**: observe that the width and height dimensions of the input image were never specified!
# more on the significance of that later.
# ## Pooling layers
# In addition to strides, another way to reduce the size of feature maps between the convolutional layers,
# is by adding **pooling** layers.
# A pooling layer has the following hyperparameters (but **no trainable parameters**):
#
# 1. Spatial extent (size) of each pooling kernel, $F \geq 2$.
# 1. Stride $S\geq 2$: spatial distance between consecutive applications.
# 1. Operation (e.g. max, average, $p$-norm)
#
# **Example**: $\max$-pooling with $F=2,~S=2$ performing a factor-2 downsample:
#
#
|
#
#
# Then, given a set of hyperparameters,
#
# - Each convolution kernel will (usually) be a tensor of shape $(C_{\mathrm{in}}, F, F)$.
# - The ouput volume dimensions will be:
#
# $$\begin{align}
# H_{\mathrm{out}} &= \left\lfloor \frac{H_{\mathrm{in}} + 2P - D\cdot(F-1) -1}{S} \right\rfloor + 1\\
# W_{\mathrm{out}} &= \left\lfloor \frac{W_{\mathrm{in}} + 2P - D\cdot(F-1) -1}{S} \right\rfloor + 1\\
# C_{\mathrm{out}} &= K\\
# \end{align}$$
# - The number of parameters in a convolutional **layer** will be:
# $$
# \underbrace{K}_{\mathrm{kernels}} \cdot \left(
# \underbrace{C_{\mathrm{in}} \cdot F^2}_{\mathrm{kernel\ parameters}} + \underbrace{1}_{\mathrm{bias\ term}}
# \right)
# $$
# **Example**: Input image is 1000x1000x3, and the first conv layer has $10$ kernels of size 5x5.
# The number of parameters in the first layer will be: $ 10 \cdot 3 \cdot 5^2 + 10 = 760 $.
#
# ### Pytorch `Conv2d` layer example
# In[3]:
import torchvision.transforms as tvtf
tf = tvtf.Compose([tvtf.ToTensor()])
ds_cifar10 = torchvision.datasets.CIFAR10(data_dir, download=True, train=True, transform=tf)
# In[4]:
# Load first CIFAR10 image
x0,y0 = ds_cifar10[0]
# add batch dimension
x0 = x0.unsqueeze(0)
# Note: channels come before spatial extent
print('x0 shape with batch dim:', x0.shape)
# In[5]:
# A function to count the number of parameters in an nn.Module.
def num_params(layer):
return sum([p.numel() for p in layer.parameters()])
# Let's create our first conv layer with pytorch:
# In[7]:
import torch.nn as nn
# First conv layer: works on input image volume
conv1 = nn.Conv2d(in_channels=x0.shape[1], out_channels=10, padding=1, kernel_size=5, stride=1,dialation=1)
print(f'conv1: {num_params(conv1)} parameters')
# Number of parameters: $10\cdot(3\cdot3^2+1)=280$
# In[8]:
# Apply the layer to an input
print(f'{"Input image shape:":25s}{x0.shape}')
y1 = conv1(x0)
print(f'{"After first conv layer:":25s}{y1.shape}')
# In[9]:
# Second conv layer: works on output volume of first layer
conv2 = nn.Conv2d(in_channels=10, out_channels=20, padding=0, kernel_size=7, stride=2)
print(f'conv2: {num_params(conv2)} parameters')
y2 = conv2(conv1(x0))
print(f'{"After second conv layer:":25s}{y2.shape}')
# New spatial extent:
#
# $$
# H_{\mathrm{out}} = \left\lfloor \frac{H_{\mathrm{in}} + 2P -F}{S} \right\rfloor + 1
# =
# \left\lfloor \frac{32 + 2\cdot 0 -6}{2} \right\rfloor + 1
# =
# 14
# $$
#
# **Note**: observe that the width and height dimensions of the input image were never specified!
# more on the significance of that later.
# ## Pooling layers
# In addition to strides, another way to reduce the size of feature maps between the convolutional layers,
# is by adding **pooling** layers.
# A pooling layer has the following hyperparameters (but **no trainable parameters**):
#
# 1. Spatial extent (size) of each pooling kernel, $F \geq 2$.
# 1. Stride $S\geq 2$: spatial distance between consecutive applications.
# 1. Operation (e.g. max, average, $p$-norm)
#
# **Example**: $\max$-pooling with $F=2,~S=2$ performing a factor-2 downsample:
#
# 












