#!/usr/bin/env python
# coding: utf-8

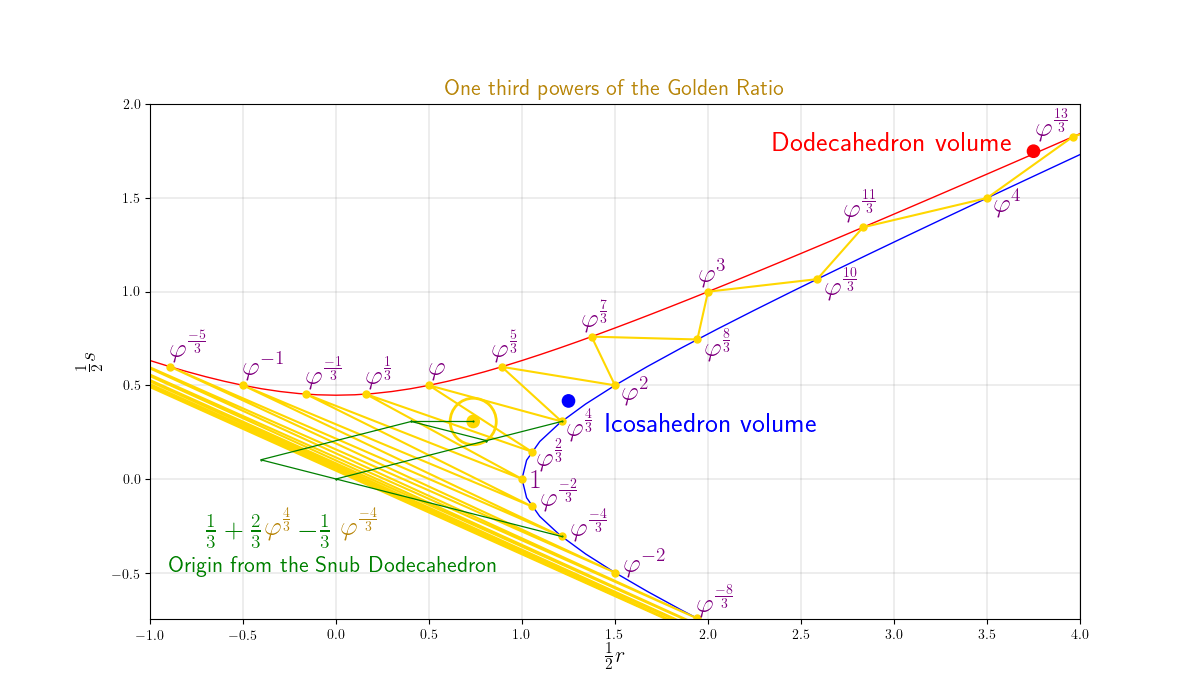
# # <center> Plot the One Third Powers of the Golden Ratio </center> 
# 
# <center>The following Python script creates this cool plot of One Third Powers of the Golden Ratio, by [Mark Adams](https://github.com/archimedeansolids)</center>
# 

# ![One_third_powers_of_the_Golden_Ratio](https://archimedeansolids.github.io/w3images/Golden_Ratio.png)

# In[ ]:


####################################################################################
#                              Golden Powers Plot                                  #
#    This Python script creates the plot of One Third Powers of the Golden Ratio   #
#                                as show here:                                     #
#            https://archimedeansolids.github.io/w3images/Golden_Ratio.png         #
#                                                                                  #
# by Mark S. Adams, markadams@gatech.edu                                           #
# ORCID iD 0000-0003-4469-051X https://orcid.org/0000-0003-4469-051X               #
####################################################################################

import os
import sys

try:
    import matplotlib
except:
    print("If matplotlib fails to import, then your Anaconda installation was not correct")
    sys.exit(1)

from distutils.spawn import find_executable
if not find_executable('latex'):
    print("*** latex is not installed ***")
    print("This matplotlib example needs latex, you will need to install latex")
    print("You can do the Texlive install directly off the internet here")
    print("https://tug.org/texlive/acquire-netinstall.html")
    print("Or, you may create a Texlive DVD from the iso file here")
    print("https://tug.org/texlive/acquire-iso.html\n")
    sys.exit(1)

try:
    import latex
except:
    print("Please wait a minute as the latex Python module is installed...")
    cmd = ('python -m pip install -U pip')
    os.system(cmd)
    cmd = ('pip install latex')
    os.system(cmd)

matplotlib.rcParams['text.usetex']=True

import matplotlib.pyplot as plt
import numpy as np

try:
    import mpmath as mp
except:
    print("Please wait a minute as mpmath is installed...")
    cmd = ('python -m pip install -U pip')
    os.system(cmd)
    cmd = ('pip install mpmath')
    os.system(cmd)
    import mpmath as mp


class GoldenThirdPower(object):
    def __init__(self, third_power_i):
        self.digits = 52
        self.third_power_i = third_power_i
        self.is_odd_power = self.third_power_i%2
        self.phi = (1 + mp.sqrt(5))/2
        self.phi_third = mp.power(self.phi, self.third_power_i/mp.mpf(3))
        self.phi_minusthird = mp.power(self.phi, self.third_power_i/mp.mpf(-3))
        if self.is_odd_power:
            self.part_r = (self.phi_third - self.phi_minusthird)/2
            self.part_s = (self.phi_third + self.phi_minusthird)/(2*mp.sqrt(5))
        else:
            self.part_r = (self.phi_third + self.phi_minusthird)/2
            self.part_s = (self.phi_third - self.phi_minusthird)/(2*mp.sqrt(5))

class GoldenThirdPowerList(object):
    def __init__(self, power_max, negative_powers_also=True):
        self.power_max = power_max
        self.negative_powers_also = negative_powers_also
        self.create_third_golden_table()

    def create_third_golden_table(self):
        self.golden_third_table = []
        if self.negative_powers_also:
            for i in range(2*self.power_max*3 + 1):  # Add one for power zero
                power = i - self.power_max*3
                self.golden_third_table.append(GoldenThirdPower(power))
        else:
            for i in range(self.power_max*3 + 1):  # Add one for power zero
                self.golden_third_table.append(GoldenThirdPower(power))
        self.table_third_r = []
        self.table_third_s = []
        for g in self.golden_third_table:
            self.table_third_r.append(g.part_r)
            self.table_third_s.append(g.part_s)

    def find_power(self, n):
        for power in self.golden_third_table:
            if power.third_power_i == n:
                return power
        return None

# Plot the powers of the Golden Ratio
powers = GoldenThirdPowerList(5)
fig = plt.figure(figsize=(12,7))
ax = fig.add_subplot(111)
fig.subplots_adjust(top=0.85)
ax.set_title('One third powers of the Golden Ratio', style='italic', fontsize=16, color='darkgoldenrod')
ax.set_xlabel(r'$\frac{1}{2}r$',fontsize=16)
ax.set_ylabel(r'$\frac{1}{2}s$',fontsize=16)
x1 = np.arange(-3, 4.5, 0.1)
y1 = np.sqrt((x1*x1 + 1)/5)
plt.plot(x1, y1, c='red', linewidth=1)
y2 = np.arange(-3, 3, 0.1)
x2 = np.sqrt(5*y2*y2 + 1)
plt.plot(x2, y2, c='blue', linewidth=1)
# plt.plot(powers.table_e, powers.table_f)
plt.plot(powers.table_third_r, powers.table_third_s, color='gold', marker='o', markersize=5)

# Plot the Origin to the Golden Ratio
power_4 = powers.find_power(4)
power_m4 = powers.find_power(-4)
if power_m4 and power_4:
    color1 = 'green'
    linewid = 0.9
    markersiz = 1
    parts_r = [0, power_4.part_r*2/3, power_4.part_r ]
    parts_s = [0, power_4.part_s*2/3, power_4.part_s ]
    plt.plot(parts_r, parts_s, marker='.', c=color1, linewidth=linewid, markersize=markersiz)
    parts_r = [power_4.part_r*2/3, power_4.part_r*2/3 -power_m4.part_r/3, -power_m4.part_r/3, 0, power_m4.part_r]
    parts_s = [power_4.part_s*2/3, power_4.part_s*2/3 - power_m4.part_s/3, -power_m4.part_s/3, 0, power_m4.part_s]
    plt.plot(parts_r, parts_s, marker='.', c=color1, linewidth=linewid, markersize=markersiz)
    parts_r = [power_4.part_r*2/3 - power_m4.part_r/3, power_4.part_r*2/3 - power_m4.part_r/3 + 1/3]
    parts_s = [power_4.part_s*2/3 - power_m4.part_s/3, power_4.part_s*2/3 - power_m4.part_s/3]
    plt.plot(parts_r, parts_s, marker='.', c=color1, linewidth=linewid, markersize=markersiz)
    x = power_4.part_r*2/3 - power_m4.part_r/3 + 1/3
    y = power_4.part_s*2/3 - power_m4.part_s/3
    k = -0.70
    n = 0.32
    m = 0.18
    o = 0.225
    ax.text(k, -0.37, r'$\frac{1}{3}+\frac{2}{3}$', fontsize=20, color='green')
    ax.text(k + n, -0.30, r'$\varphi^{\frac{4}{3}}$', fontsize=20, color='darkgoldenrod')
    ax.text(k + n + m, -0.37, r'$-\frac{1}{3}$', fontsize=20, color='green')
    ax.text(k + n + m + o, -0.30, r'$\varphi^{\frac{-4}{3}}$', fontsize=20, color='darkgoldenrod')
    ax.text(-0.9, -0.5, r'Origin from the Snub Dodecahedron', fontsize=16, color=color1)
    circle1 = plt.Circle((x, y), 0.124, color='gold', fill=False, lw="2")
    ax.add_artist(circle1)
    circle2 = plt.Circle((x, y), 0.0329, color='gold')
    ax.add_artist(circle2)
    x = 15/12
    y = 5/12
    circle2 = plt.Circle((x, y), 0.0329, color='blue')
    ax.add_artist(circle2)
    x = 15/4
    y = 7/4
    circle2 = plt.Circle((x, y), 0.0329, color='red')
    ax.add_artist(circle2)
    xx1 = 1.45
    yy1 = 0.25
    ax.text(xx1, yy1, r'Icosahedron volume', fontsize=20, color='blue')
    xx2 = 2.35
    yy2 = 1.75
    ax.text(xx2, yy2, r'Dodecahedron volume', fontsize=20, color='red')

phi_offsets = [
    [0.0, 0.03],
    [0.0, 0.05],
    [0.05, 0.0],
    [0.0, 0.05],
    [0.05, 0.0],
    [0.0, 0.05],
    [0.05, 0.0],
    [0.0, 0.05],
    [0.05, -0.05], # 0
    [0.0, 0.05],
    [0.03, -0.08],
    [0.0, 0.05],
    [0.03, -0.08], #4/3
    [-0.05, 0.05],
    [0.04, -0.08], #2
    [-0.05, 0.05],
    [0.04, -0.09], #8/3
    [-0.05, 0.05],
    [0.04, -0.09], #10/3
    [-0.1, 0.05],
    [0.04, -0.08], #4
    [-0.2, 0.0],
    [0.1, 0.0],
]

# Label the golden ratio points
firstpower = -8
for i, offset in enumerate(phi_offsets):
    n = i+firstpower
    power = powers.find_power(n)
    if power:
        if (n==-7):
            continue
        text = r'$\varphi^{\frac{%d}{3}}$'%(n)
        if not (n%3):
            text = r'$\varphi^{%d}$'%(n/3)
        if (n==0):
            text = r'$1$'
        if (n==3):
            text = r'$\varphi$'
        ax.text(power.part_r+offset[0], power.part_s+offset[1], text,
            fontsize=20, color='#800080')

# Plot axis and Show
ax.axis([-1, 4, -.75, 2])
ax.set_xticks(np.arange( -1, 4.5, 0.5))
ax.set_yticks(np.arange(-.5, 2.5, 0.5))
ax.grid(which='major', linestyle='-', linewidth='0.2', color='gray')
plt.show()