#!/usr/bin/env python
# coding: utf-8
# # Nonlinear equation I
# * Find roots of $f(x)$. That is, find the value of $x$ so that $f(x)=0$.
# * All nonlinear algebraic problems can be written in the form $f(x)=0$. Just move all terms to one side of the equation.
# * Numerical methods for nonlinear problems proceed by setting an initial guess for the solution, and iterating to improve the guess until some desired error tolerance is achieved.
# * Open and Closed domain methods.
# * Here:
# * discuss closed domain methods
# * one equation in one unknown
#
#
# ## Bound the solution
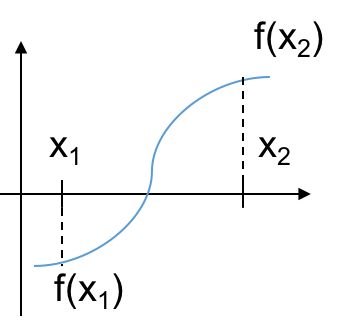
# * Bracket the root:
# * Choose two guesses for the solution: $x_1$ and $x_2$. If $f(x_1)\cdot f(x_2)<0$ then the two guesses bracket the root.
# * This implies that the root is between the two guesses.
#  #
#
# ### Procedures
# * Graph it.
# * Visual picture can be very helpful.
# * Provides an intial guess of the root.
# * Indicates the function behavior, and possible problem areas.
# * May not be practical, however.
# * Cost of function evaluation may be excessive.
#
# * Do a simple incremental search.
# * Simply set a small $\Delta x$ and search the domain for $f(x)=0$.
# * Obviously not very practical.
#
# * Past experience
# * Output of one problem may be a good guess for the input of another problem.
# * This especially true in cases where we do multiple solves, which is quite common.
# * Use intuition:
# * species mass fractions should be between 0 and 1.
# * most temperatures in K should be in reasonable ranges.
#
# * Solve a simpler problem to get a guess for the harder problem.
# * For example, if solving for a nonideal gas, get an initial guess using an ideal gas.
# * Another example, if solving for temperature with a variable heat capacity, find a temperature guess using a constant heat capacity, which results in an easy linear solve for the guess.
# * In combustion, we might solve using a simple 1-step reaction mechanism, instead of a more complex 400 step mechanism.
# ### Once you have a bracket refine the root
# * Reduce the size of the interval, while maintaining the bracket.
# * Two methods: **bisection**, and **regula falsi (false position)**
# * These are robust (they work!), but they are not overly fast.
#
# ## Bisection
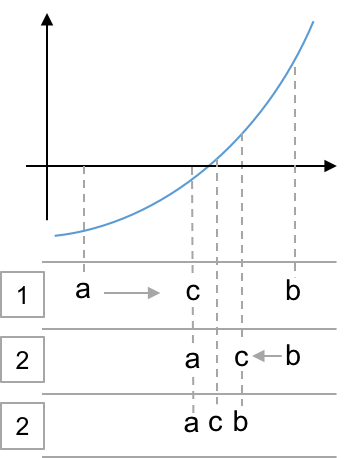
# * Guess two points that bracket the root: $a$, $b$
# * Check for $f(a)=0$ or $f(b)=0$
# * Bracket tests:
# * $f(a)f(b)<0$
# * ($f(a)>0$ and $f(b)<0$) or ($f(a)<0$ and $f(b)>0$)
# * Refine: $c = (a+b)/2$
# * Select new bracket:
# * if $f(a)f(c) < 0 \rightarrow b=c$
# * else $a=c$
#
#
#
#
# ### Procedures
# * Graph it.
# * Visual picture can be very helpful.
# * Provides an intial guess of the root.
# * Indicates the function behavior, and possible problem areas.
# * May not be practical, however.
# * Cost of function evaluation may be excessive.
#
# * Do a simple incremental search.
# * Simply set a small $\Delta x$ and search the domain for $f(x)=0$.
# * Obviously not very practical.
#
# * Past experience
# * Output of one problem may be a good guess for the input of another problem.
# * This especially true in cases where we do multiple solves, which is quite common.
# * Use intuition:
# * species mass fractions should be between 0 and 1.
# * most temperatures in K should be in reasonable ranges.
#
# * Solve a simpler problem to get a guess for the harder problem.
# * For example, if solving for a nonideal gas, get an initial guess using an ideal gas.
# * Another example, if solving for temperature with a variable heat capacity, find a temperature guess using a constant heat capacity, which results in an easy linear solve for the guess.
# * In combustion, we might solve using a simple 1-step reaction mechanism, instead of a more complex 400 step mechanism.
# ### Once you have a bracket refine the root
# * Reduce the size of the interval, while maintaining the bracket.
# * Two methods: **bisection**, and **regula falsi (false position)**
# * These are robust (they work!), but they are not overly fast.
#
# ## Bisection
# * Guess two points that bracket the root: $a$, $b$
# * Check for $f(a)=0$ or $f(b)=0$
# * Bracket tests:
# * $f(a)f(b)<0$
# * ($f(a)>0$ and $f(b)<0$) or ($f(a)<0$ and $f(b)>0$)
# * Refine: $c = (a+b)/2$
# * Select new bracket:
# * if $f(a)f(c) < 0 \rightarrow b=c$
# * else $a=c$
#
#  # ### Error
# * The error is always bounded by $\epsilon_n\le|b-a|$
# * $\epsilon_{n+1} = \epsilon_n/2$ $\rightarrow$ linear convergence.
# * $\epsilon_0$, $\epsilon_1=\epsilon_0/2$, $\epsilon_2 = \epsilon_1/2 = \epsilon_0/4 = \epsilon_0/2^2$
# * $\rightarrow \epsilon_n = \epsilon_0/2^n$.
# * Hence:
# $$n = \log_2\left(\frac{\epsilon_0}{\epsilon_n}\right)$$
# * That is, to reduce the error from $\epsilon_0 \le |a-b|$ to some desired $\epsilon_n$ requires $n=\log_2(\epsilon_0/\epsilon_n)$ iterations.
#
# ## Regula Falsi
# * Rather than bisect the interval to find $c$, draw an intersecting line between $f(a)$ and $f(b)$ as an approximation to the function.
#
# ### Error
# * The error is always bounded by $\epsilon_n\le|b-a|$
# * $\epsilon_{n+1} = \epsilon_n/2$ $\rightarrow$ linear convergence.
# * $\epsilon_0$, $\epsilon_1=\epsilon_0/2$, $\epsilon_2 = \epsilon_1/2 = \epsilon_0/4 = \epsilon_0/2^2$
# * $\rightarrow \epsilon_n = \epsilon_0/2^n$.
# * Hence:
# $$n = \log_2\left(\frac{\epsilon_0}{\epsilon_n}\right)$$
# * That is, to reduce the error from $\epsilon_0 \le |a-b|$ to some desired $\epsilon_n$ requires $n=\log_2(\epsilon_0/\epsilon_n)$ iterations.
#
# ## Regula Falsi
# * Rather than bisect the interval to find $c$, draw an intersecting line between $f(a)$ and $f(b)$ as an approximation to the function.
# 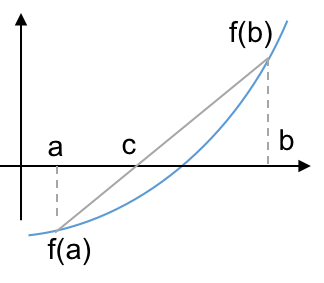 #
# * Solve the root of this linear approximation:
# * that is, where the line intersects the x-axis where $y=f(x)$ is zero.
# * Equation for the line:
# $$f_l(x) = f(a) + \frac{f(b)-f(a)}{b-a}(x-a).$$
# * Then let $f_l(c)=0$ and solve for $c$ to get:
# $$ c= a - f(a)\frac{b-a}{f(b)-f(a)}.$$
# * To retain the bracket, replace $a$ or $b$ with $c$ as for bisection.
#
#
#
# * Solve the root of this linear approximation:
# * that is, where the line intersects the x-axis where $y=f(x)$ is zero.
# * Equation for the line:
# $$f_l(x) = f(a) + \frac{f(b)-f(a)}{b-a}(x-a).$$
# * Then let $f_l(c)=0$ and solve for $c$ to get:
# $$ c= a - f(a)\frac{b-a}{f(b)-f(a)}.$$
# * To retain the bracket, replace $a$ or $b$ with $c$ as for bisection.
#
# 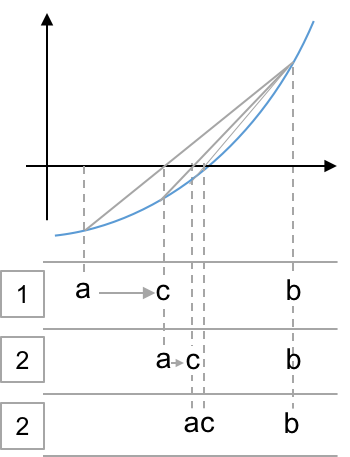 # * Robust
# * Usually faster than bisection
# * No error bound though.
# * May get superlinear convergence
# * Keeping the old versus new function evaluation...
# * Consider the following case though (slow):
#
# * Robust
# * Usually faster than bisection
# * No error bound though.
# * May get superlinear convergence
# * Keeping the old versus new function evaluation...
# * Consider the following case though (slow):
#  # ## Convergence
# * When to stop?
# * $|b-a| < \epsilon$
# * absolute error
# * works for $x=1$
# * not so good for $x=10^{20}$
# * $|b-a|/|c| < \epsilon$
# * relative error
# * $|f(c)|< \epsilon$
# * error in function versus error in root.
#
# Consider:
#
# ## Convergence
# * When to stop?
# * $|b-a| < \epsilon$
# * absolute error
# * works for $x=1$
# * not so good for $x=10^{20}$
# * $|b-a|/|c| < \epsilon$
# * relative error
# * $|f(c)|< \epsilon$
# * error in function versus error in root.
#
# Consider:
#  #
# * On the left, the bracket is narrow, but the function is not zero.
# * On the right, the function is near zero, but the bracket is not narrow.
# * Do both $|b-a|/|c| < \epsilon_1$ and $|f(c)|<\epsilon_2$.
# ## Bisection example
#
# Find root of $f(x)=(x-2)^2 - 1$.
# In[ ]:
# In[ ]:
# ## Compare with ```fsolve```
# In[ ]:
#
# * On the left, the bracket is narrow, but the function is not zero.
# * On the right, the function is near zero, but the bracket is not narrow.
# * Do both $|b-a|/|c| < \epsilon_1$ and $|f(c)|<\epsilon_2$.
# ## Bisection example
#
# Find root of $f(x)=(x-2)^2 - 1$.
# In[ ]:
# In[ ]:
# ## Compare with ```fsolve```
# In[ ]:
 #
#
# ### Procedures
# * Graph it.
# * Visual picture can be very helpful.
# * Provides an intial guess of the root.
# * Indicates the function behavior, and possible problem areas.
# * May not be practical, however.
# * Cost of function evaluation may be excessive.
#
# * Do a simple incremental search.
# * Simply set a small $\Delta x$ and search the domain for $f(x)=0$.
# * Obviously not very practical.
#
# * Past experience
# * Output of one problem may be a good guess for the input of another problem.
# * This especially true in cases where we do multiple solves, which is quite common.
# * Use intuition:
# * species mass fractions should be between 0 and 1.
# * most temperatures in K should be in reasonable ranges.
#
# * Solve a simpler problem to get a guess for the harder problem.
# * For example, if solving for a nonideal gas, get an initial guess using an ideal gas.
# * Another example, if solving for temperature with a variable heat capacity, find a temperature guess using a constant heat capacity, which results in an easy linear solve for the guess.
# * In combustion, we might solve using a simple 1-step reaction mechanism, instead of a more complex 400 step mechanism.
# ### Once you have a bracket refine the root
# * Reduce the size of the interval, while maintaining the bracket.
# * Two methods: **bisection**, and **regula falsi (false position)**
# * These are robust (they work!), but they are not overly fast.
#
# ## Bisection
# * Guess two points that bracket the root: $a$, $b$
# * Check for $f(a)=0$ or $f(b)=0$
# * Bracket tests:
# * $f(a)f(b)<0$
# * ($f(a)>0$ and $f(b)<0$) or ($f(a)<0$ and $f(b)>0$)
# * Refine: $c = (a+b)/2$
# * Select new bracket:
# * if $f(a)f(c) < 0 \rightarrow b=c$
# * else $a=c$
#
#
#
#
# ### Procedures
# * Graph it.
# * Visual picture can be very helpful.
# * Provides an intial guess of the root.
# * Indicates the function behavior, and possible problem areas.
# * May not be practical, however.
# * Cost of function evaluation may be excessive.
#
# * Do a simple incremental search.
# * Simply set a small $\Delta x$ and search the domain for $f(x)=0$.
# * Obviously not very practical.
#
# * Past experience
# * Output of one problem may be a good guess for the input of another problem.
# * This especially true in cases where we do multiple solves, which is quite common.
# * Use intuition:
# * species mass fractions should be between 0 and 1.
# * most temperatures in K should be in reasonable ranges.
#
# * Solve a simpler problem to get a guess for the harder problem.
# * For example, if solving for a nonideal gas, get an initial guess using an ideal gas.
# * Another example, if solving for temperature with a variable heat capacity, find a temperature guess using a constant heat capacity, which results in an easy linear solve for the guess.
# * In combustion, we might solve using a simple 1-step reaction mechanism, instead of a more complex 400 step mechanism.
# ### Once you have a bracket refine the root
# * Reduce the size of the interval, while maintaining the bracket.
# * Two methods: **bisection**, and **regula falsi (false position)**
# * These are robust (they work!), but they are not overly fast.
#
# ## Bisection
# * Guess two points that bracket the root: $a$, $b$
# * Check for $f(a)=0$ or $f(b)=0$
# * Bracket tests:
# * $f(a)f(b)<0$
# * ($f(a)>0$ and $f(b)<0$) or ($f(a)<0$ and $f(b)>0$)
# * Refine: $c = (a+b)/2$
# * Select new bracket:
# * if $f(a)f(c) < 0 \rightarrow b=c$
# * else $a=c$
#
#  # ### Error
# * The error is always bounded by $\epsilon_n\le|b-a|$
# * $\epsilon_{n+1} = \epsilon_n/2$ $\rightarrow$ linear convergence.
# * $\epsilon_0$, $\epsilon_1=\epsilon_0/2$, $\epsilon_2 = \epsilon_1/2 = \epsilon_0/4 = \epsilon_0/2^2$
# * $\rightarrow \epsilon_n = \epsilon_0/2^n$.
# * Hence:
# $$n = \log_2\left(\frac{\epsilon_0}{\epsilon_n}\right)$$
# * That is, to reduce the error from $\epsilon_0 \le |a-b|$ to some desired $\epsilon_n$ requires $n=\log_2(\epsilon_0/\epsilon_n)$ iterations.
#
# ## Regula Falsi
# * Rather than bisect the interval to find $c$, draw an intersecting line between $f(a)$ and $f(b)$ as an approximation to the function.
#
# ### Error
# * The error is always bounded by $\epsilon_n\le|b-a|$
# * $\epsilon_{n+1} = \epsilon_n/2$ $\rightarrow$ linear convergence.
# * $\epsilon_0$, $\epsilon_1=\epsilon_0/2$, $\epsilon_2 = \epsilon_1/2 = \epsilon_0/4 = \epsilon_0/2^2$
# * $\rightarrow \epsilon_n = \epsilon_0/2^n$.
# * Hence:
# $$n = \log_2\left(\frac{\epsilon_0}{\epsilon_n}\right)$$
# * That is, to reduce the error from $\epsilon_0 \le |a-b|$ to some desired $\epsilon_n$ requires $n=\log_2(\epsilon_0/\epsilon_n)$ iterations.
#
# ## Regula Falsi
# * Rather than bisect the interval to find $c$, draw an intersecting line between $f(a)$ and $f(b)$ as an approximation to the function.
#  #
# * Solve the root of this linear approximation:
# * that is, where the line intersects the x-axis where $y=f(x)$ is zero.
# * Equation for the line:
# $$f_l(x) = f(a) + \frac{f(b)-f(a)}{b-a}(x-a).$$
# * Then let $f_l(c)=0$ and solve for $c$ to get:
# $$ c= a - f(a)\frac{b-a}{f(b)-f(a)}.$$
# * To retain the bracket, replace $a$ or $b$ with $c$ as for bisection.
#
#
#
# * Solve the root of this linear approximation:
# * that is, where the line intersects the x-axis where $y=f(x)$ is zero.
# * Equation for the line:
# $$f_l(x) = f(a) + \frac{f(b)-f(a)}{b-a}(x-a).$$
# * Then let $f_l(c)=0$ and solve for $c$ to get:
# $$ c= a - f(a)\frac{b-a}{f(b)-f(a)}.$$
# * To retain the bracket, replace $a$ or $b$ with $c$ as for bisection.
#
#  # * Robust
# * Usually faster than bisection
# * No error bound though.
# * May get superlinear convergence
# * Keeping the old versus new function evaluation...
# * Consider the following case though (slow):
#
# * Robust
# * Usually faster than bisection
# * No error bound though.
# * May get superlinear convergence
# * Keeping the old versus new function evaluation...
# * Consider the following case though (slow):
#  # ## Convergence
# * When to stop?
# * $|b-a| < \epsilon$
# * absolute error
# * works for $x=1$
# * not so good for $x=10^{20}$
# * $|b-a|/|c| < \epsilon$
# * relative error
# * $|f(c)|< \epsilon$
# * error in function versus error in root.
#
# Consider:
#
# ## Convergence
# * When to stop?
# * $|b-a| < \epsilon$
# * absolute error
# * works for $x=1$
# * not so good for $x=10^{20}$
# * $|b-a|/|c| < \epsilon$
# * relative error
# * $|f(c)|< \epsilon$
# * error in function versus error in root.
#
# Consider:
#  #
# * On the left, the bracket is narrow, but the function is not zero.
# * On the right, the function is near zero, but the bracket is not narrow.
# * Do both $|b-a|/|c| < \epsilon_1$ and $|f(c)|<\epsilon_2$.
# ## Bisection example
#
# Find root of $f(x)=(x-2)^2 - 1$.
# In[ ]:
# In[ ]:
# ## Compare with ```fsolve```
# In[ ]:
#
# * On the left, the bracket is narrow, but the function is not zero.
# * On the right, the function is near zero, but the bracket is not narrow.
# * Do both $|b-a|/|c| < \epsilon_1$ and $|f(c)|<\epsilon_2$.
# ## Bisection example
#
# Find root of $f(x)=(x-2)^2 - 1$.
# In[ ]:
# In[ ]:
# ## Compare with ```fsolve```
# In[ ]: