#!/usr/bin/env python
# coding: utf-8

# # ODEs: Higher order IVP

# * EE and IE are simple, but low order: globally first order.
#     * To get high accuracy requires many more steps: smaller $\Delta t$.
#     * Higher order methods give the same accuracy for larger step sizes.
# 
# 

# 
# ## Second order methods
# 
# ODE:
# $$\frac{dy}{dt} = f(y,t),$$
# $$y(t=0) = y_0.$$
# 

# 
# ### Modified midpoint (MM) method
# 
# * EE takes a step from $k$ to $k+1$ using the slope at point $k$.
# * IE takes a step from $k$ to $k+1$ using the slope at point $k+1$.
# * MM takes a step from $k$ to $k+1$ using the slope at point $k+1/2$.
#     * To get to $k+1/2$ so that we can evaluate the slope there, take a trial EE step to that point
#     
# <font color='blue'>
# $$y_{k+1/2} = y_k + \frac{\Delta t}{2}f(y_k,t_k).$$
# $$y_{k+1}   = y_k + \Delta tf(y_{k+1/2},t_{k+1/2}).$$
# </font>
# 
# * So, on each step we first evaluate $y_{k+1/2}$ using EE for a half step. Then we take the real full step using the slope at $y_{k+1/2}$.

# #### Taylor series representation
# * Write two Taylor series approximations for $y_{k+1}$ and $y_k$ centered on $y_{k+1/2}$.
# $$y_{k+1} = y_{k+1/2} + y^{\prime}_{k+1/2}\frac{\Delta t}{2} + \frac{1}{2}y^{\prime\prime}_{k+1/2}\left(\frac{\Delta t}{2}\right)^2+\frac{1}{6}y^{\prime\prime\prime}_{k+1/2}\left(\frac{\Delta t}{2}\right)^3\ldots,$$
# $$y_{k} = y_{k+1/2} - y^{\prime}_{k+1/2}\frac{\Delta t}{2} + \frac{1}{2}y^{\prime\prime}_{k+1/2}\left(\frac{\Delta t}{2}\right)^2-\frac{1}{6}y^{\prime\prime\prime}_{k+1/2}\left(\frac{\Delta t}{2}\right)^3\ldots,$$
# * Subtract the second equation from the first and solve for $y_{k+1}$.
# $$y_{k+1} = y_k + \Delta t y^{\prime}_{k+1/2} + \mathcal{O}(\Delta t^3).$$
# * The method is globally $\mathcal{O}(\Delta t^2)$.
# * Note, $y^{\prime}_{k+1/2} \equiv f(y_{k+1/2},t_{k+1/2}).$
# * Note, this analysis was done using $y_{k+1/2}$, but the actual method doesn't use $y_{k+1/2}$, it uses the EE approximation to this value, so we really have
# $$y_{k+1} = y_k + \Delta t (y^{\prime}_{k+1/2}+\mathcal{O}(\Delta t^2)) + \mathcal{O}(\Delta t^3),$$
# where the $\mathcal{O}(\Delta t^2)$ term is the local error of the EE method. When we expand this we get  
# $$y_{k+1} = y_k + \Delta t y^{\prime}_{k+1/2}+\mathcal{O}(\Delta t^3) + \mathcal{O}(\Delta t^3) = y_k + \Delta ty^{\prime}_{k+1/2}+\mathcal{O}(\Delta t^3),$$
# so there is no overall change in the global order of the method.

# ### Implicit trapazoid (IT) method
# * From the MM method:
# $$ y_{k+1} = y_k + \Delta t y^{\prime}_{k+1/2} = y_k + \Delta t f_{k+1/2}.$$
# * Evaluate 
# $$f_{k+1/2} = \frac{1}{2}(f_k + f_{k+1}).$$
# * Hence,
# 
# <font color='blue'>
# $$y_{k+1} = y_k + \Delta t\frac{f(y_k,t_k) + f(y_{k+1},t_{k+1})}{2}.$$
# </font>
# 
# * This method is globally $\mathcal{O}(\Delta t^2)$ accurate.
# * Note how and why the method is implicit.
# * Note, this method can also be written as EE from $k$ to $k+1/2$ followed by IE from $k+1/2$ to $k+1$:
# $$y_{k+1/2} = y_k + \frac{\Delta t}{2}f_k,$$
# $$y_{k+1} = y_{k+1/2} + \frac{\Delta t}{2}f_{k+1}.$$
# 
# 

# ### Modified Euler (ME) method
# * This is like the IT method, but get $f_{k+1}$ from a full EE step:
# 
# <font color='blue'>
# $$ y^*_{k+1} = y_k + \Delta t f_k,$$
# $$ y_{k+1} = y_k + \Delta t \frac{f(y_k,t_k) + f(y_{k+1}^*,t_{k+1})}{2}.$$
# </font>
# 
# * This is a two-step **predictor-corrector** method. We predict the answer using EE in the first step, then using this result, we improve (correct) the answer in the second step.
# * This method is globally $\mathcal{O}(\Delta t^2)$ accurate.

# ## Runge Kutta (RK) methods
# 
# \begin{align*}
# y_{k+1} = y_k + &hS, \\
# & S = c_1S_1 + c_2S_2 + c_3S_3 + \ldots.
# \end{align*}
# 
# * Here, let $h\equiv\Delta t$
# * $S$ is a slope $dy/dt$, evaluated from $f(y,t)$ or from a combination of $f(y,t)$ evaluated at various points $y$ in different ways. 
#     * The $c_i$ above are coefficients of the linear combination.
# * Here, we will ignore the time dependence of $f$ for simplicity and clarity.

# ### Second order
# \begin{align*}
# y_{k+1} = &y_k + h(c_1S_1 + c_2S_2), \\
# &S_1 = f(y_k), \\
# &S_2 = f(y_k + \beta hS_1).
# \end{align*}
# * So, we are taking linear combinations of $h$ times the slopes evaluated at different points.
# * Note in the second equation we evaluate the slope at a later time. We get to that time by taking an Euler-like step $y_k+\beta hS_1$.
# * Combine the above equations:
# 
# <font color='blue'>
# $$ y_{k+1} = y_k + c_1hf(y_k) + c_2hf(y_k+\beta hS_1).$$
# </font>
# 

# * Again (for slides display): 
# 
# <font color='blue'>
# $$ y_{k+1} = y_k + c_1hf(y_k) + c_2hf(y_k+\beta hS_1).$$
# </font>
# 
# * This equation contains parts at point $k$ and a part at a later time, $f(y_k+\beta hS_1)$.
#     * Note that $\beta hS_1 = \beta hf_k$.
# * We can write all parts at point $k$ by expanding $f(y_k+\beta hS_1)$ in a Taylor series about point $k$:
# 
# \begin{align}
# f(y_k+\beta\Delta y_1) &= f_k + \left.\frac{\partial f}{\partial y}\right|_k\beta hS_1 + \mathcal{O}(h^2), \\
# &= f_k + \beta h f_{y,k} f_k + \mathcal{O}(h^2),\\
# \end{align}
# 
# where $f_{y,k}$ is the derivative of $f$ with respect to $y$ evaluated at point $k$.
# 
# * Hence,
# 
# <font color='green'>
# $$ y_{k+1} = y_k + f_k h(c_1+c_2) + \beta h^2c_2f_{y,k}f_k + \mathcal{O}(h^3).$$
# </font>
# 

# 
# * Now, we will take a Taylor series of $y_{k+1}$ and compare it with the above green equation.
# 
#     \begin{align}
#     y_{k+1} &= y_k + y_k^{\prime}h + \frac{1}{2} y_k^{\prime\prime}h^2 + \mathcal{O}(h^3),\\
#     &= y_k + f_kh + \frac{1}{2}h^2(y^{\prime})^{\prime}_k + \mathcal{O}(h^3).
#     \end{align}
# 
#     * Now,
#   
#     $$(y^{\prime})^{\prime} = \left.\frac{\partial f}{\partial t}\right|_k = \left.\frac{\partial f}{\partial y}\frac{dy}{dt}\right|_k = f_{y,k}f_k.$$
#     
#     * Hence:
#     
#     <font color='red'>
#     $$y_{k+1} = y_k + f_kh + \frac{1}{2}h^2f_{y,k}f_k + \mathcal{O}(h^3).$$
#     </font>
# 
# * Again, the green equation above is:
# 
# <font color='green'>
# $$ y_{k+1} = y_k + f_k h(c_1+c_2) + \beta h^2c_2f_{y,k}f_k + \mathcal{O}(h^3).$$
# </font>
# 
# * Comparing the green and red equations imples:
# 
# <font color='blue'>
# $$ (c_1+c_2) = 1, $$
# $$\beta c_2 = \frac{1}{2}.$$
# </font>
# 
# * So, in choosing our second order RK method, we have one degree of freedom. Choose, say, $c_1$, then $c_2 = 1-c_1$, and then $\beta = 1/2c_2.$
#     * There are an infinite number of possible second order methods.

# ### Example
# Recall our 2nd order method:
# \begin{align*}
# y_{k+1} = &y_k + h(c_1S_1 + c_2S_2), \\
# &S_1 = f(y_k), \\
# &S_2 = f(y_k + \beta hS_1).
# \end{align*}
# 
# * Let $c_1 = 1/2$, then $c_2=1/2$ and $\beta = 1$.
# $$y_{k+1} = y_k + \frac{h}{2}(f(y_k) + f(y_k+hf(y_k))$$
# * This is the ME method.

# ### Fourth order RK method (*The* RK method)
# 
# \begin{align*}
# y_{k+1} &= y_k + h\left(\frac{1}{6}S_1 + \frac{2}{6}S_2 + \frac{2}{6}S_3 + \frac{1}{6}S_4\right),\\
# & S_1 = f(y_k), \\
# & S_2 = f(y_k+\frac{h}{2}S_1), \\
# & S_3 = f(y_k+\frac{h}{2}S_2), \\
# & S_4 = f(y_k+hS_3). 
# \end{align*}
# 
# <img src="https://ignite.byu.edu/che541/lectures/figs/l13f01.png" width="250">

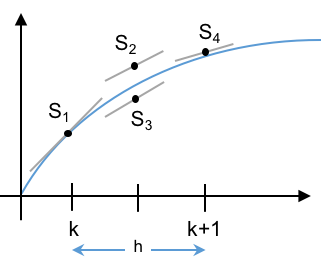# ### Approach
# * Evaluate the slope $S_1$ at $y_k$.
# * Take a half step EE from point $k$ to $k+1/2$ using slope $S_1$. 
#     * Evaluate $S_2$ here.
# * Take a half step EE from point $k$ to $k+1/2$ using slope $S_2$. 
#     * Evaluate $S_3$ here.
# * Take a full step EE from point $k$ to $k+1$ using slope $S_3$. 
#     * Evaluate $S_4$ here.
# * Take the final full step using a linear combination of the slopes:
# $$y_{k+1} = y_k + \frac{h}{6}(S_1 + 2S_2 + 2S_3+ S_4).$$
# * Note how values of $y$ at intermediate step are used to compute slopes for following steps.
# * For $n^{th}$ order with $n\le 4$ $\rightarrow$ $n$ function evaluations are required.
# * For $>4^{th}$ order $\rightarrow$ more than $n$ function evaluations required. (Storage costs too).
# * $\rightarrow$ the $4^{th}$ order method gives the most bang for the buck.

# ### RK4 code
# * Solve $dy/dt = -y$ from $t=0$ to $t=5$ with RK4 and EE. Use 10 steps, so $\Delta t = 0.5$. Let $y_0=1$.

# In[1]:


import numpy as np
import matplotlib.pyplot as plt
get_ipython().run_line_magic('matplotlib', 'inline')


# In[2]:


def odeRK4(f, y0, t):
    ns = len(t)-1
    y = np.zeros(ns+1)
    y[0] = y0
    
    for k in range(ns):
        h = t[k+1]-t[k]
        S1 = f(y[k],t[k])
        S2 = f(y[k]+0.5*h*S1, t[k]+0.5*h)
        S3 = f(y[k]+0.5*h*S2, t[k]+0.5*h)
        S4 = f(y[k]+    h*S3, t[k]+    h)
        y[k+1] = y[k] + h/6*(S1 + 2*S2 + 2*S3 + S4)
        
    return y


# In[4]:


def odeEE(f, y0, t):
    ns = len(t)-1
    y = np.zeros(ns+1)
    y[0] = y0
    
    for k in range(ns):
        h = t[k+1]-t[k]
        y[k+1] = y[k] + h*f(y[k],t[k])
    
    return y


# In[5]:


def f(y, t):
    return -y

#----------------------

y0    = 1.0
tend  = 5.0
t     = np.linspace(0,tend,11)

#----------------------

y_RK4 = odeRK4(f,y0,t)
y_EE  = odeEE(f,y0,t)

tt      = np.linspace(0,tend,100)
y_Exact = np.exp(-tt)

#----------------------


# In[6]:


plt.rc('font', size=14)
plt.plot(tt,y_Exact,'k--')
plt.plot(t, y_RK4,  'o')
plt.plot(t, y_EE,   '^')
plt.legend(['exact', 'RK4', 'EE'], frameon=False)
plt.ylabel('y')
plt.xlabel('t');


# In[ ]: