#!/usr/bin/env python
# coding: utf-8
# # Introduction to scientific computing with Python
# *Maxime Sangnier*
#
# September, 2024
#
# ## Part 1: Basics of Python
# # Table of contents
# 1. [What is and why Python](#part1)
# - [Overview](#part1sec1)
# - [Comparison with other languages](#part1sec2)
# 1. [Practical points](#part2)
# - [Versions of Python](#part2sec1)
# - [Installation](#part2sec2)
# - [Usage](#part2sec3)
# - [Getting help](#part2sec4)
# 1. [An introduction to JupyterLab](#part3)
# - [Survival kit](#part3sec1)
# - [Useful features](#part3sec2)
# - [Text and equations](#part3sec3)
# 1. [Basics of the Python language](#part4)
# - [Numbers](#part4sec1)
# - [Data structures](#part4sec2)
# - [Conditional statements](#part4sec3)
# - [For loop](#part4sec4)
# - [While loop](#part4sec5)
# - [Function](#part4sec6)
# - [Modules](#part4sec7)
# 1. [Exercises](#part5)
# - [Exercise 1](#part5sec1)
# - [Exercise 2](#part5sec2)
# - [Exercise 3](#part5sec3)
# - [Exercise 4](#part5sec4)
# - [Exercise 5](#part5sec5)
# - [Exercise 6](#part5sec6)
# 1. [References](#part6)
#
# # What is and why Python
# ## Overview
# For scientific computing, one mainly needs three things:
# - workable toolboxes to applied mathematics, such as for sampling data, loading real-world data, processing, visualizing and analyzing them, solving equations, computing Fourier transformations, manipulating mathematical objects (polynomials, matrices, tensors), etc.
# - a perfect trade-off between power and easiness of the programming language (scientists are not developers);
# - efficient computations: code should execute quickly.
#
# As a consequence, a good language for scientific computing should gather these three aspects while providing also easy ways of communicating with collaborators (and students), as well as re-using and maintaining ad-hoc code produced by researchers.
# Python (in union with IPython and available packages such as Scipy) is a scripting language that is suitable for scientific computing regarding the previous requirements.
# The reasons of its popularity in the scientific community are that Python:
# - is free and open-source, making its development fast and the Python community excited;
# - comes with a rich collection of packages for scientific computing (not exhaustive yet);
# - can do much more than scientific computing (web server management, data bases, etc.). This is very useful since scientists interact with other domains of computer science;
# - is easy to learn, easy to write and easy to read;
# - can be structured and maintained efficiently (packages, modules, object oriented programming);
# - quite fast to execute thanks to a *precompilation*;
# - computationally demanding parts can be converted from Python to C ([Cython](http://cython.org/)).
#
# However, Python has also some drawbacks.
# In particular, it:
# - requires a more advanced knowledge in development (low-level commands, many types and containers) than other scientific languages such as Matlab and R, even though it is few compared to C;
# - comes with less packages than Matlab and R *in their own domain of research*;
# - is a language in progress. In particular, differences between Python 2 (still often used by operating systems) and Python 3 (used by researchers and scientists) can confuse the practitioner.
#
# ## Comparison with other languages
# ### R
# Advantages:
# - free and open-source;
# - very advanced features for statistics.
#
# Drawbacks:
# - the language is not so powerful;
# - dedicated to a single domain (statistics).
#
# ### Matlab
# Advantages:
# - rich collection of toolboxes for many scientific domains. Each toolbox contains implementations of numerous common algorithms;
# - by default linked with a fast linear algebra library ([MKL](https://software.intel.com/en-us/intel-mkl));
# - easy to learn, easy to write (not so easy to read).
#
# Drawbacks:
# - not free;
# - parallel computation not available in the base version;
# - language not so powerful.
#
# ### C, C++
# Advantages:
# - very fast execution (optimized compilers). Such a compiled language serves as a baseline for measuring running times of implementations;
# - common and very powerful language.
#
# Drawbacks:
# - may be difficult to learn (language addressed to developers);
# - painful usage: no interactivity, compilation mandatory.
#
# # Practical points
# ## Versions of Python
# There are currently two versions of Python: 2 and 3.
# The most commonly used version in the research and industrial community is now Python 3, even though Python 2 may still be the default choice on several operating systems.
#
# Let us remark that Python 3 is not backwards-compatible (see [differences between both versions](https://docs.python.org/3/whatsnew/3.0.html)).
# In practice, this means that a Python 2 script cannot always be interpreted by Python 3 (and respectively).
#
# In this tutorial, we focus on Python 3.
#
# ## Installation
# ### Windows and macOS
# A Python essential kit can be easily obtained by installing [Anaconda](https://docs.anaconda.com/anaconda/install/).
# It includes all you need for scientific computing.
# In addition, an alternative to Anaconda is [Enthought Canopy](https://store.enthought.com/downloads/#default).
# Even though it is a commercial product, Canopy is free for academic purposes.
# Finally, another workable option on Windows is [Python(x,y)](http://python-xy.github.io/).
#
# ### Linux
# On Debian and Ubuntu, a good option is to install Python and its package manager pip:
#
# sudo apt-get install python3 python3-pip spyder3
#
# Then, use pip to install the packages needed for scientific computing:
#
# sudo pip3 install jupyterlab numpy scipy matplotlib pillow scikit-learn seaborn pandas statsmodels cvxopt ipympl tensorflow
#
# If you have trouble installing a package, use instead:
#
# sudo apt-get install python3-[package_name]
#
# ## Usage
# Since Python is a scripting language, there are several ways to use it.
# The main ones are detailed below.
#
# ### Command line
# In a shell, execute:
#
# python3
#
# Then, start using it:
#
# a = 3.14
# print("hello world")
#
#  #
# Press CTRL+D or type:
#
# quit()
#
# to exit.
#
# If your code is written in a file *script.py*, you can run it from a shell with:
#
# python3 script.py
#
# or in Python with:
#
# execfile('script.py')
#
# ### IPython
# [IPython](http://ipython.org/) is a powerful interactive shell that comes with numerous useful features such as:
# - interactivity;
# - tab-completion;
# - command history;
# - object introspection;
# - special (magic) commands;
# - numbered input/output.
#
#
#
# Press CTRL+D or type:
#
# quit()
#
# to exit.
#
# If your code is written in a file *script.py*, you can run it from a shell with:
#
# python3 script.py
#
# or in Python with:
#
# execfile('script.py')
#
# ### IPython
# [IPython](http://ipython.org/) is a powerful interactive shell that comes with numerous useful features such as:
# - interactivity;
# - tab-completion;
# - command history;
# - object introspection;
# - special (magic) commands;
# - numbered input/output.
#
# 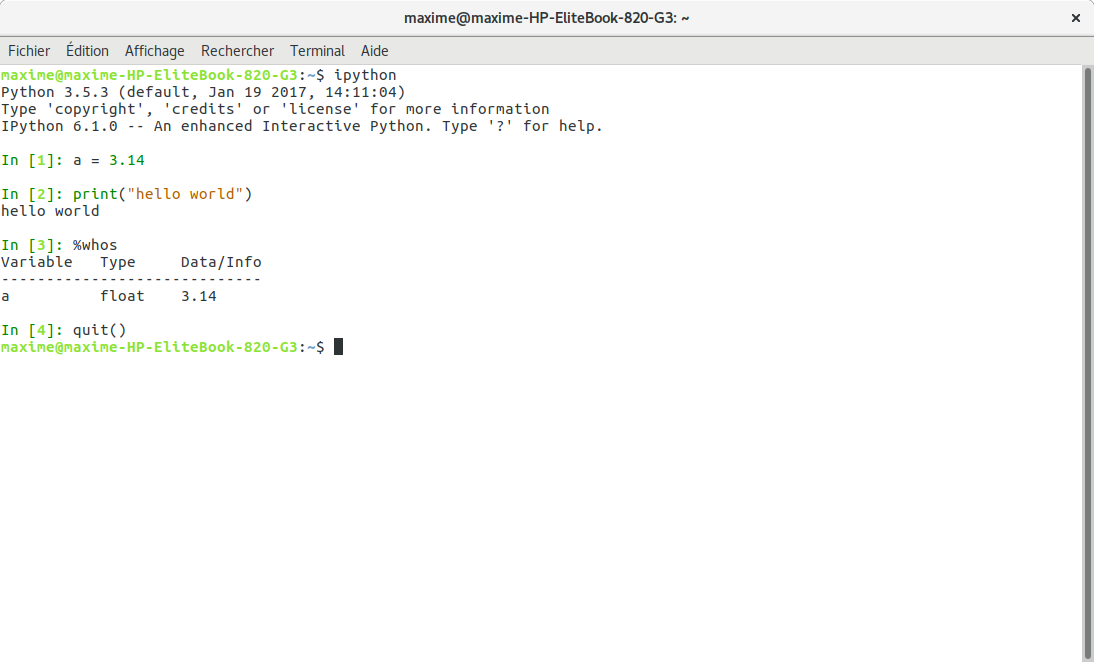 #
# One can use up and down arrows to access command history, tab for completion and %[command] for [magic commands](http://ipython.org/ipython-doc/3/interactive/magics.html) (or directly [command]).
# The most used are:
# - *cd [path]*: change the current working directory;
# - *history*: print input history;
# - *load [file]*: load code into the current frontend;
# - *matplotlib [gui]*: set up matplotlib to work interactively;
# - *pwd*: return the current working directory path;
# - *reset*: reset the namespace;
# - *run [file]*: run the script inside IPython as a program;
# - *whos*: print all interactive variables with extra information.
#
# To run a script, use:
#
# run script.py
#
# ### Spyder
# [Spyder](http://pythonhosted.org/spyder/) is a Matlab-like IDE that shows both an editor and a Python shell.
# It is an efficient tool for developing and testing codes.
#
#
#
# One can use up and down arrows to access command history, tab for completion and %[command] for [magic commands](http://ipython.org/ipython-doc/3/interactive/magics.html) (or directly [command]).
# The most used are:
# - *cd [path]*: change the current working directory;
# - *history*: print input history;
# - *load [file]*: load code into the current frontend;
# - *matplotlib [gui]*: set up matplotlib to work interactively;
# - *pwd*: return the current working directory path;
# - *reset*: reset the namespace;
# - *run [file]*: run the script inside IPython as a program;
# - *whos*: print all interactive variables with extra information.
#
# To run a script, use:
#
# run script.py
#
# ### Spyder
# [Spyder](http://pythonhosted.org/spyder/) is a Matlab-like IDE that shows both an editor and a Python shell.
# It is an efficient tool for developing and testing codes.
#
# 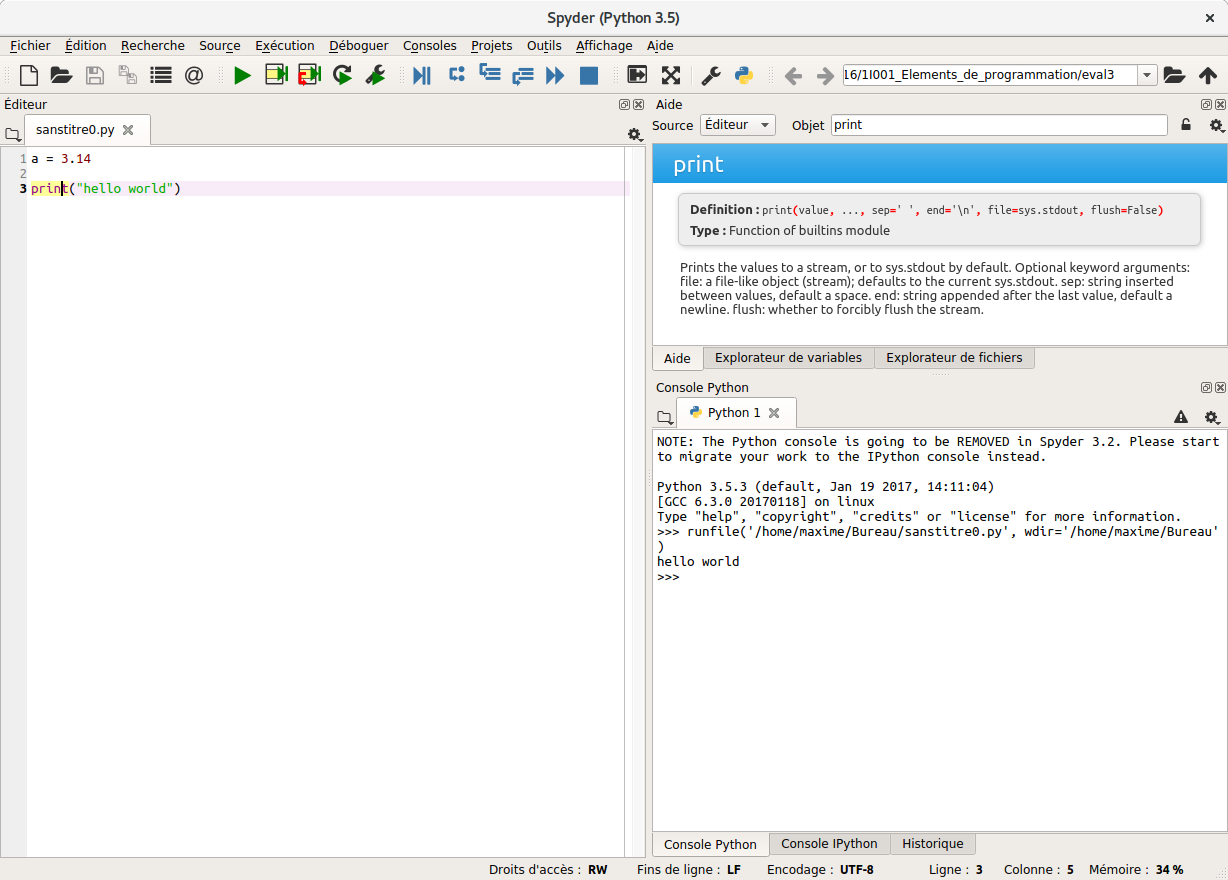 # In particular feature, it enables to run only part of the script while keeping the previous results (variable states) in memory.
#
# To run a script, you can edit it and press F5.
# If you want to execute only a selection of it, select the part of interest and press F9.
#
# ### JupyterLab
# JupyterLab is a novel web-based IDE to produce easy-to-read reports with text, equations, code and results (called a notebook).
# This is what is used here!
#
#
# In particular feature, it enables to run only part of the script while keeping the previous results (variable states) in memory.
#
# To run a script, you can edit it and press F5.
# If you want to execute only a selection of it, select the part of interest and press F9.
#
# ### JupyterLab
# JupyterLab is a novel web-based IDE to produce easy-to-read reports with text, equations, code and results (called a notebook).
# This is what is used here!
#
# 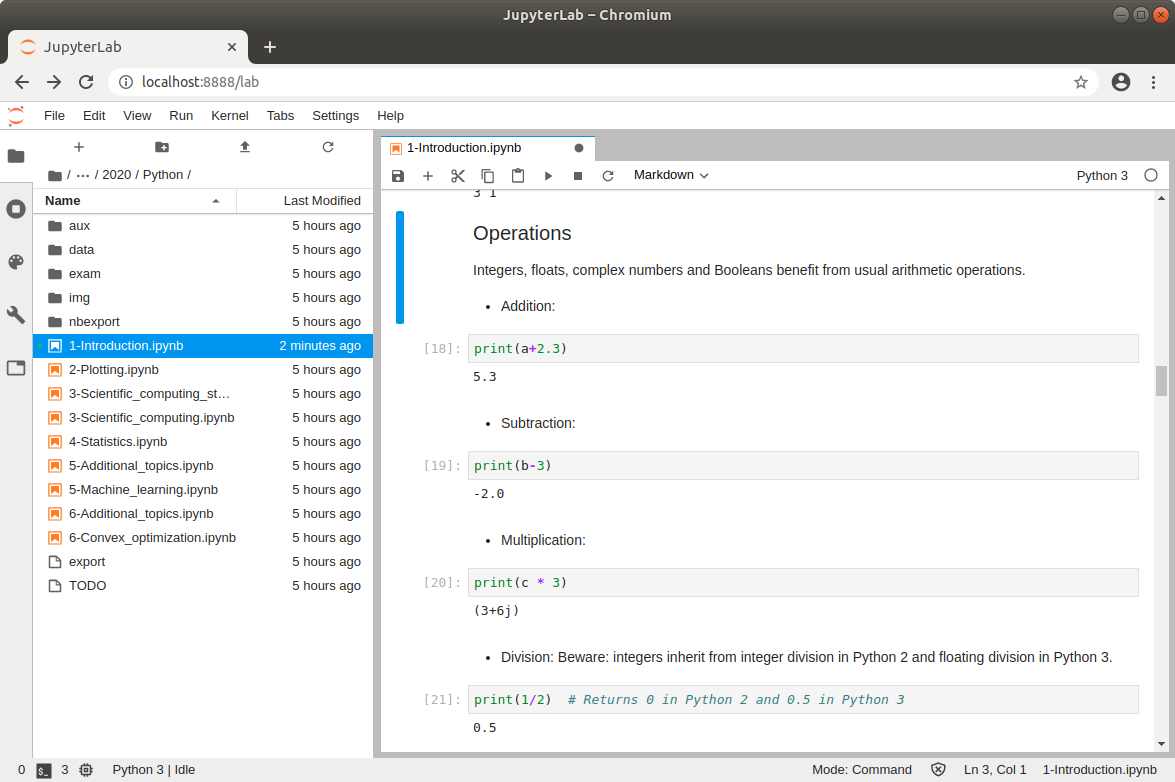 #
# To launch it, write in a shell:
#
# jupyter-lab
#
# ## Getting help
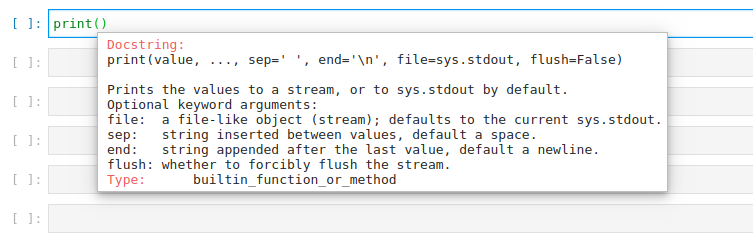
# Python and related modules are very well documented in local (docstrings) and on the Internet (documentation on the Internet may be clearer and updated compared to the local one).
# To access the docstring, use *help*:
# In[1]:
help(print)
# In a notebook (or IPython), you can also use *?*:
# In[2]:
get_ipython().run_line_magic('pinfo', 'print')
# or SHIFT+TAB:
#
#
#
# To launch it, write in a shell:
#
# jupyter-lab
#
# ## Getting help
# Python and related modules are very well documented in local (docstrings) and on the Internet (documentation on the Internet may be clearer and updated compared to the local one).
# To access the docstring, use *help*:
# In[1]:
help(print)
# In a notebook (or IPython), you can also use *?*:
# In[2]:
get_ipython().run_line_magic('pinfo', 'print')
# or SHIFT+TAB:
#
#  # Otherwise, you can search the net for an answer.
# The easiest way is to google your query: [vandermonde matrix python](https://www.google.fr/?client=ubuntu#channel=fs&q=vandermonde+matrix+python&gfe_rd=cr).
#
# Finally, you can go directly to a package documentation website.
# The following links provide the documentation of the packages used in this introduction (see next sections for details on the packages):
# - [official documentation](https://docs.python.org/3.5/tutorial/index.html);
# - [Scipy](http://docs.scipy.org/doc/scipy/reference/);
# - [Numpy](http://docs.scipy.org/doc/numpy/reference/);
# - [Statsmodels](http://www.statsmodels.org/stable/index.html);
# - [Scikit-learn](http://scikit-learn.org/stable/documentation.html).
#
# # An introduction to JupyterLab
# A notebook is a sequence of cells that may be of two types:
# - code: it enables to edit, execute and see the output of a small Python script;
# - markdown: if offers a way to write text and equations, as well as to import images.
#
# ## Survival kit
# A Jupyter notebook can be modified in two modes:
# - the command mode: we can add, delete and modify cells;
# - the edit mode: we can edit and run the script inside a cell.
#
# The forthcoming sections describe the most useful keyboard shortcuts.
# An exhaustive list of the available actions and shortcuts can be found by hitting the palette in the menu bar (or CTRL+SHIFT+C).
#
# It is highly recommended to experience these shortcuts on your own on the test cell below.
#
# ### Command shortcuts
# If you are in the edit mode, press ESC to enter the command mode.
#
# - To edit a cell (enter the edit mode), go to the desired cell and press ENTER.
# - To add a cell below, press B.
# - To add a cell above, press A.
# - To cut a cell, press X.
# - To copy a cell, press C.
# - To paste a cell below, press V.
# - To delete a cell, press DD.
# - To convert a cell to a markdown cell, press M.
# - To convert a cell to a code cell, press Y.
#
# ### Edit shortcuts
# If you are in the command mode, press ENTER to enter the edit mode.
#
# - To run a cell, press CTRL+ENTER.
# - To run a cell and select the one below, press SHIFT+ENTER.
# - To run a cell and add one below, press ALT+ENTER.
# - To apply autocompletion, press TAB at the end of the word. For example, write "pri", then press TAB.
# It gives "print".
# - To get an inline help, press SHIFT+TAB.
# - To indent several lines, select them and press TAB.
# - To dedent several lines, select them and press SHIFT+TAB.
# - To (un)comment a line (or several ones after selection), press CTRL+/.
# - To exit the edit mode, press ESC.
#
# In[3]:
print("This is a test cell")
# ## Useful features
# ### Code console
# You can open a code console by clicking the + button in the file browser and selecting the kernel.
# It enables you to run interactively small part of codes in a console, keeping the history in full view.
#
# Such a code console can also be opened or linked to a Python file.
# This is a way to run a part of code directly from a Python file.
# To do so, when editing this file, right-click in it and select *Create Console for Editor*. Then, select a single line or a block of code and send it to the code console by hitting SHIFT+ENTER.
#
# ### Mirrored output
# You can create a new synchronized view of a cell output by right-clicking a cell and hitting *Create New View for Output*.
# This view can then be moved to a separate tab.
# ## Text and equations
# By default, cells are for code but they can be converted to markdown cells (see the shortcut above).
# Markdown cells accept both [Markdown](https://jupyter-notebook.readthedocs.io/en/stable/examples/Notebook/Working%20With%20Markdown%20Cells.html) (text formatting) and [$\LaTeX$](https://fr.wikipedia.org/wiki/Aide:Formules_TeX) (equations).
#
# ### General formatting
# Headings are defined with the symbol `#`:
#
# # First level
# ## Second level
# ### Third level
# #### Fourth level
# ##### Fifth level
#
# Even though paragraphs are defined automatically, you can force a line break with the code `
# Otherwise, you can search the net for an answer.
# The easiest way is to google your query: [vandermonde matrix python](https://www.google.fr/?client=ubuntu#channel=fs&q=vandermonde+matrix+python&gfe_rd=cr).
#
# Finally, you can go directly to a package documentation website.
# The following links provide the documentation of the packages used in this introduction (see next sections for details on the packages):
# - [official documentation](https://docs.python.org/3.5/tutorial/index.html);
# - [Scipy](http://docs.scipy.org/doc/scipy/reference/);
# - [Numpy](http://docs.scipy.org/doc/numpy/reference/);
# - [Statsmodels](http://www.statsmodels.org/stable/index.html);
# - [Scikit-learn](http://scikit-learn.org/stable/documentation.html).
#
# # An introduction to JupyterLab
# A notebook is a sequence of cells that may be of two types:
# - code: it enables to edit, execute and see the output of a small Python script;
# - markdown: if offers a way to write text and equations, as well as to import images.
#
# ## Survival kit
# A Jupyter notebook can be modified in two modes:
# - the command mode: we can add, delete and modify cells;
# - the edit mode: we can edit and run the script inside a cell.
#
# The forthcoming sections describe the most useful keyboard shortcuts.
# An exhaustive list of the available actions and shortcuts can be found by hitting the palette in the menu bar (or CTRL+SHIFT+C).
#
# It is highly recommended to experience these shortcuts on your own on the test cell below.
#
# ### Command shortcuts
# If you are in the edit mode, press ESC to enter the command mode.
#
# - To edit a cell (enter the edit mode), go to the desired cell and press ENTER.
# - To add a cell below, press B.
# - To add a cell above, press A.
# - To cut a cell, press X.
# - To copy a cell, press C.
# - To paste a cell below, press V.
# - To delete a cell, press DD.
# - To convert a cell to a markdown cell, press M.
# - To convert a cell to a code cell, press Y.
#
# ### Edit shortcuts
# If you are in the command mode, press ENTER to enter the edit mode.
#
# - To run a cell, press CTRL+ENTER.
# - To run a cell and select the one below, press SHIFT+ENTER.
# - To run a cell and add one below, press ALT+ENTER.
# - To apply autocompletion, press TAB at the end of the word. For example, write "pri", then press TAB.
# It gives "print".
# - To get an inline help, press SHIFT+TAB.
# - To indent several lines, select them and press TAB.
# - To dedent several lines, select them and press SHIFT+TAB.
# - To (un)comment a line (or several ones after selection), press CTRL+/.
# - To exit the edit mode, press ESC.
#
# In[3]:
print("This is a test cell")
# ## Useful features
# ### Code console
# You can open a code console by clicking the + button in the file browser and selecting the kernel.
# It enables you to run interactively small part of codes in a console, keeping the history in full view.
#
# Such a code console can also be opened or linked to a Python file.
# This is a way to run a part of code directly from a Python file.
# To do so, when editing this file, right-click in it and select *Create Console for Editor*. Then, select a single line or a block of code and send it to the code console by hitting SHIFT+ENTER.
#
# ### Mirrored output
# You can create a new synchronized view of a cell output by right-clicking a cell and hitting *Create New View for Output*.
# This view can then be moved to a separate tab.
# ## Text and equations
# By default, cells are for code but they can be converted to markdown cells (see the shortcut above).
# Markdown cells accept both [Markdown](https://jupyter-notebook.readthedocs.io/en/stable/examples/Notebook/Working%20With%20Markdown%20Cells.html) (text formatting) and [$\LaTeX$](https://fr.wikipedia.org/wiki/Aide:Formules_TeX) (equations).
#
# ### General formatting
# Headings are defined with the symbol `#`:
#
# # First level
# ## Second level
# ### Third level
# #### Fourth level
# ##### Fifth level
#
# Even though paragraphs are defined automatically, you can force a line break with the code `
` or draw a horizontal line with `***`.
# ***
#
# ### Items, emphasis and colors
# Lists can be characterized by bullets, using `-`:
# - Bullet 1;
# - Bullet 2;
# or by numbers, using `1.`:
# 1. first item;
# 1. second item.
#
# Lists can also be nested thanks to indented symbols:
# - Bullet 1;
# 1. Item 1;
# 2. Item 2.
# - Bullet 2;
# 1. a single item.
#
# Emphasis can be done by **bold** (using `**text**`) or *italic* font (using `*text*`).
#
# Colors are defined by the code `text`.
# This has to be used carefully since it is more html code than Markdown scripting.
#
# ### Raw text and quoting
# You can use inline raw text for path and file names using the single quote symbol ` or indentation for blocs.
#
# For instance, this is a `# raw text`, while this is a raw bloc:
#
# raw text
# with multiple lines.
#
# You can also quote by using `>`:
#
# > A mathematician is a device for turning coffee into theorems.
# Paul Erdos
#
# ### Images and references
#
# You can add an image with ``:
#
# 
#
# > Picture by [Vincent Delerm](http://vincent-delerm.com/).
#
# You may also use ` ` to resize the image.
#
#
#
#
#
# References can be made to external links with `[text](URL)` and to internal labels with `[text](#label)`, where a tag `` has been put somewhere in the notebook.
#
# ### Equations
# Equations should be written in the $\LaTeX$ language, for which help is [available](https://fr.wikipedia.org/wiki/Aide:Formules_TeX).
# If you know the symbol and want to obtain the $\LaTeX$ command, you can [detexify](http://detexify.kirelabs.org/classify.html) it.
#
# You only need basics of $\LaTeX$:
# - Inline equation with `$equation$`: $x = \sqrt{2}$.
# - Centered equation with
#
#
# $$
# [equation]
# $$
#
# For instance:
# $$
# \int_0^1 1 \, dx = 1.
# $$
# - Multiple line equation with
#
#
# \begin{align}
# item &= item \\
# &= item.
# \end{align}
#
# For instance:
# \begin{align}
# \int_0^1 1 \, dx &= \frac{1}{2} \int_0^1 2 \, dx\\
# &= \frac{1}{2} \cdot 2 \\
# &= 1.
# \end{align}
# - Exponents and subscripts with `^` and `_`: $x_{i}^2$.
# - Summation and product with `\sum_{i=1}^n` and `\prod_{i=1}^n`: $\sum_{i=1}^n \prod_{j=1}^m x_{ij}$.
# - Real numbers with `\mathbb`: $\forall x \in \mathbb R^d$.
# - Calligraphic letters with `\mathcal`: $\mathcal N(0, 1)$.
# - Big parentheses with `\left(… \right)`: $\left( \frac{1}{n} \sum_{i=1}^n x_i \right)$.
# # Basics of the Python language
# ## Numbers
# ### Integer, floats and complex
# In[4]:
a = 1 # Integer
b = 1. # Float
c = 1.+2.j # Complex
# In[5]:
print(a)
type(a)
# In[6]:
print(b)
type(b)
# In[7]:
print(c)
type(c)
# In[8]:
print(c.real, c.imag)
# **Question**
#
# What are the result and the type of the following expressions:
# - 3+5.;
# - 16 * 4;
# - 8 / 2;
# - 2 * 10 / 2?
# In[ ]:
# Answer
# ### Booleans
# In[10]:
test = True
type(test)
# In[11]:
print(test and a == 1)
# In[12]:
print(test or a == 2)
# In[13]:
print(a != 1)
# In[14]:
print(test and not a == 1)
# A Boolean is a number:
# In[15]:
print(int(test)) # Cast Boolean to int
# In[16]:
print(test+1, test-1, test*3.2)
# **Question**
#
# Write an expression that returns:
# - $-1$ if $x \le -1$;
# - $1$ if $x \ge 1$;
# - x otherwise.
# In[ ]:
# Answer
# ### Swap variables in a concise manner
# In[18]:
abis = 3
print(a, abis)
a, abis = abis, a # Swap variables
print(a, abis)
# ### Operations
# Integers, floats, complex numbers and Booleans benefit from usual arithmetic operations.
#
# - Addition:
# In[19]:
print(a+2.3)
# - Subtraction:
# In[20]:
print(b-3)
# - Multiplication:
# In[21]:
print(c * 3)
# - Division:
# Beware: integers inherit from integer division in Python 2 and floating division in Python 3.
# In[22]:
print(1/2) # Returns 0 in Python 2 and 0.5 in Python 3
# A good practice is to use floating numbers:
# In[23]:
print(1./2)
print(a/2.)
# As well as explicit integer division (note that the result is of type *int*):
# In[24]:
a = 3//2
print(a, type(a))
# - Power:
# In[25]:
print(10**3)
# - Modulo:
# In[26]:
print(5%2)
# **Question**
#
# Given two integers $x$ and $y$ such that $x \ge y$, compute and print the quotient of the Euclidean division of $x$ by $y$.
# Do the same for the remainder (with two different expressions).
# In[ ]:
# Answer
# ## Data structures
# ### Strings
# Strings are immutable objects (they cannot be modified), that can be defined with simple, double or triple quotes.
# Simple and double quotes are equivalent:
# In[28]:
test1 = "Wilcoxon"
test2 = 'Chi2'
print(test1)
# … Except for quotes themselves.
# We write:
# In[29]:
print("\"" + " or " + '"')
# And:
# In[30]:
print('\'' + ' or ' + "'")
# Triple quotes allow to have several lines:
# In[31]:
txt1 = """This is
a Wilcoxon test"""
print(txt1)
# This is equivalent to using the special character *\\n*:
# In[32]:
txt2 = "This is\na Chi2 test"
print(txt2)
# #### Operations on strings
# Strings can be concatenated and repeated.
# In[33]:
print(test1 + ", p=" + str(0.1)) # Concatenation
print(test2 * 3) # Repetition
# We can change the case of a string.
# In[34]:
print(test1.lower())
print(test2.upper())
print("mr. ".capitalize() + "tickle".capitalize())
# Strings can be joined with a given separator.
# In[35]:
"-".join([test1, test2])
# **Question**
#
# Given the three variables below, produce the string:
#
# outcome ~ xx + yy + zz
# In[36]:
x = "Xx"
y = "YY"
z = "zZ"
# In[ ]:
# Answer
# #### String formatting and printing
# Python 3 provides an improved string formatting syntax, called f-string.
# In a nutshell, it is enough to put an *f* at the beginning and curly braces around expressions that should be replaced with their values.
# In[38]:
print(f"The first test is {test1}, while the second is {test2}.")
# Multiline f-strings are allowed:
# In[39]:
pval = 0.03
(f"The p-value for the {test1} test is: "
f"{pval}")
# Or escaping a return with *\*:
# In[40]:
f"The p-value for the {test1} test is: " \
f"{pval}"
# Using triple " will lead to:
# In[41]:
print(f"""The p-value for the {test1} test is:
{pval}""")
# Format specifiers: `{value:{width}.{precision}}` can be used, mainly for numbers:
# In[42]:
root = 0.123456789
print(f"The root is {root:.3f}.")
print(f"The root is {root:.2e}.")
print(f"The root is {root:10.2f}.")
# For a full support, see the [Format Specification Mini-Language](https://docs.python.org/3.6/library/string.html#formatspec).
# Strings can also be formatted in the old way:
# In[43]:
print("The first test is {}, while the second is {}.".format(test1, test2)) # With positional arguments
print("The first test is {1}, while the second is {0}.".format(test1, test2)) # With numbered arguments
print("The first test is {T1}, while the second is {T2}."
.format(T1=test1, T2=test2)) # With keywords arguments
print("The first test is {}, while the second is {T2}."
.format(test1, T2=test2))
print("The root is {}.".format(0.123456789)) # Numbers can be printed directly or converted
print("The root is {0:.3f}.".format(0.123456789))
print("The root is {0:.2e}.".format(0.123456789))
print("The root is {0:10.2f}.".format(0.123456789))
# In the expression *x:y.zA*,
# - *x* is the positioning parameter;
# - *y* is the (minimum) number of (potentially blank) numbers before .;
# - *z* is the (maximum) number of numbers after .;
# - *A* is the formatting letter:
# - f: float;
# - e: exponential notation;
# - d: integer.
# Strings can also be formatted in the very old way:
# In[44]:
print("An integer: %d" % 2)
print("A float: %f" % 0.123456789)
print("A short float: %0.2f" % 0.123456789)
print("A nice p-value: %0.1e" % 0.05)
print("%s is %d years old" % ("Robert", 64))
# When several arguments are given, *print* prints them all (the behavior is slightly different between Python 2 and Python 3).
# In[45]:
print("string 1", "string 2")
# One can also control the end character:
# In[46]:
print("Something to say", end="") # Python 3
#print("Something to say"), # Python 2
print("… and something else")
# **Remark:** objects can be printed simply by evaluating them:
# In[47]:
test1
# To remove this side effect, use a semicolon:
# In[48]:
test1;
# **Question**
#
# Given the three variables below, produce the sentence:
#
# The expression x+y*z = 3+1.4142*5 approximately equals 1.01e+01.
# In[49]:
x = 3
y = 2**0.5
z = 5
# In[ ]:
# Answer
# ### List
# A list is an ordered collection of items, that may have different types.
# A list is a mutable object and can thus be modified.
# In[51]:
l = [1, 3, 5, 7, "odd numbers"]
print(l)
# #### Indexing and slicing
# Indexing starts at 0.
# In[52]:
print("First item: ", l[0]) # First item
print("Last item: ", l[-1]) # Last item
# The slicing syntax is: `l[start:stop:stride]`.
# If some arguments are omitted, they are replaced by the *natural* ones (`start=0`, `stride=1`).
# In[53]:
print("First two items: ", l[:2]) # Equivalent to l[0:2]
print("Sublists: ", l[::2], l[1:3]) # First sublist equivalent to l[0::2]
print("Reverse: ", l[::-1])
# Note that, when slicing, the last element is not considered.
# In[54]:
print(l[0:2]) # Items numbered 0 and 1 (2 excluded)
print(l[2:]) # All items after number 2 included
print(l[2:-1]) # All items after number 2 included, last item exluced
# **Question**
#
# Given the list below (of size denoted by $n$), print its head (the first $n-1$ items) and its tail (the last $n-1$ items).
# In[55]:
x = [5, 3, 7, 8, 3, 4, 6]
# In[ ]:
# Answer
# #### Concatenation, extension and repetition
# In[57]:
l = l+[9] # Concatenation
print(l)
# In[58]:
l += [11] # Concatenation
print(l)
# Extension is an in-place operation.
# In[59]:
l.extend(["extension"]) # Extension
print(l)
# In[60]:
l *= 2 # Repetition
print(l)
# #### Adding, deleting and indexing an item
# In[61]:
l.append(13) # Add an item at the end of the list
print(l)
# In[62]:
del l[0] # Delete the first item
print(l)
# In[63]:
print("9 is in position", l.index(9))
# **Question**
#
# Move the first item of $x$ to the last position.
# In[64]:
x = [5, 3, 7, 8, 3, 4, 6]
# In[ ]:
# Answer
# #### Presence
# In[66]:
print("2 is in l: ", 2 in l)
print("3 is in l: ", 3 in l)
# #### Other operations
# In[67]:
print(len(l))
# In[68]:
l.reverse()
print(l)
# More details: use *help(list)* or *list?* in Ipython and Jupyter notebook.
# ### Tuple
# Roughly speaking, a tuple is an immutable list (it cannot be changed).
# It can be defined in two ways:
# In[69]:
t = (1, 2) # Definition with parentheses
type(t)
# In[70]:
t = 1, 2 # Light definition
print(t)
# In[71]:
t += ("three",) # Concatenation with a singleton
print(t)
print("Length: ", len(t)) # Length
# In[72]:
t0, t1, t2 = t # Unpacking
print(t0, t1, t2)
# ### Sets
# A set is an unordered collection of unique items.
# Usual mathematical operations (union, difference) can be performed.
# In[73]:
odd = set([1, 3, 5, 5])
even = set([2, 4])
type(odd)
print(odd)
# In[74]:
print(odd - set([1])) # Difference of sets
# In[75]:
print(odd | even) # Union of sets
# In[76]:
odd.add(2)
print(odd & even) # Intersection of sets
# In[77]:
print(odd ^ even) # Complementary of the intersection of sets
# **Question**
#
# Print items that are simultaneously in $x$ and $y$.
# In[78]:
x = [5, 3, 7, 8, 3, 4, 6]
y = [1, 9, 3, 7, 6, 2]
# In[ ]:
# Answer
# ### Dictionary
# A dictionary is a table key/value.
# Keys can be any immutable type (string, numbers, …).
# In[80]:
d = {'x': [[1, -0.5], [-2, 1]], 'y': [0, 1]} # Definition
print(d['x'])
# In[81]:
d[10] = "ten" # Add an item
print(d)
# In[82]:
# Print keys and values
print(d.keys())
print(d.values())
# In[83]:
"x" in d # Check if a key is in the dictionary
# **Question**
#
# Add a new item to the dictionary defined below, with key "sigma2" and value $sigma^2$.
# Set $mu$ to $0$ and print the final dictionary.
# In[84]:
db = {'mu': 3, 'sigma': 1.5}
# In[ ]:
# Answer
# ### Assignment operator
# In Python the assignment operator `=` is used for two purposes:
# - modifying attributes and items of mutable objects;
# - binding a name to a value.
#
# The last point means that **`=` does not make a copy** but creates a new alias for an already existing value.
#
# Examples:
# - Immutable objects:
# In[86]:
a = 1.1
b = a
b is a # two names, same data (in memory)
# In[87]:
print(id(a), id(b))
# In[88]:
a = "monday"
b = a
b is a # two names, same data (in memory)
# In[89]:
a = 3, 10
b = a
b is a # two names, same data (in memory)
# - Mutable objects:
# In[90]:
a = [1, 2]
b = a
b is a # two names, same data (in memory)
# In[91]:
b[-1] = 3
print(a)
print(b)
# Modifications appear on both a and b (same data).
# To make a copy, use:
# In[92]:
b = a.copy() # In Python 3
#b = a[:] # In Python 2
b is a
# In[93]:
b[-1] = 2
print(a)
print(b)
# *a* and *b* are two different objects.
#
# This is the same for dictionaries and sets:
# In[94]:
a = {"k": 1}
b = a
b is a
# In[95]:
b = a.copy()
b is a
# In[96]:
a = set([1, 2])
b = a
b is a
# In[97]:
b = a.copy()
b is a
# ## Conditional statements
# In Python, the blocks of the control flows are delimited by indentation.
# See for instance the use of `if/elif/else` statement.
# The comparisons are made with `==`, `!=`, `is`, `in`, `not`, `<`, `<=`, …
# In[98]:
h = 3.14 # Target
i = 3 # Guess
print("The target is", end=" ")
if h < i:
print("less than %d." % i)
elif h > i:
print("greater than %d." % i)
else:
print("exactly %d." % i)
# **Question**
#
# Write a conditional statement that:
# - add y to x if y is missing in x;
# - change y to -y in x otherwise.
# In[99]:
x = [4, 2, 7]
y = 6
# In[ ]:
# Answer
# ### Evaluating objects
# `if [object]` is false for
# - 0, 0.0 numbers;
# - empty structures;
# - False and None;
#
# and true otherwise.
#
# **Example**: checking if a list is empty.
# In[101]:
a = []
if not a:
print("Empty list.")
# **Question**
#
# Write a script that prints the result of the operation $x/y$ if $y \neq 0$ and "infinity" otherwise.
# In[ ]:
# Answer
# ### Assignment operator
# Conditional statements can also be used in union with the assignment operator:
# In[104]:
res = "greater or equal" if h >= i else "less"
print("The target is " + res + " than %d." % i)
# ## For loop
# Example of a for loop:
# In[105]:
for it in range(10):
print(it, end=" ")
else:
print("\nthe loop was not broken")
# Here, the optional `else` part is executed when the loop goes until the end.
# If the loop is broken (such as in the following example), the `else` part is not executed.
# Besides `break`, another interested keyword is `continue`. It skips the end of the current iteration.
# In[106]:
for it in range(10):
if it % 2 == 0: # Even numbers
continue
if it > 8:
break
print(it, end=" ")
else:
print("\nthe loop was not broken")
# A special feature of Python is to being able to iterate over the items of any sequence (range, list, tuple, dictionary, …).
#
# ### Range
# The syntax for the range function is:
# `range(stop)` or `rang(start, stop, step)` with third parameter optional.
# In[107]:
for it in range(5):
print(it, end=" ")
# In[108]:
for it in range(10, 20, 3):
print(it, end=" ")
# ### List
# In[109]:
for car in ['WV', 'BMW', 2016]:
print(car)
# ### Tuple
# In[110]:
for it in ("My favorite number", "is", 7):
print(it, end=" ")
# ### Dictionary
# In[111]:
conf = {"Name": "NIPS", "Date": 2016, "Location": "Barcelona"}
for key in conf:
print(key)
# In[112]:
for key, value in conf.items():
print(key, ":", value)
# In[113]:
for key, value in sorted(conf.items()):
print(key, ":", value)
# **Question**
#
# Compute and print the first 10 items of the sequence
# $$
# \begin{cases}
# u_0 &=& 0 \\
# u_{n+1} &=& 3u_n+2, \forall n \in \mathbb N.
# \end{cases}
# $$
# In[ ]:
# Answer
# ### Useful commands: enumerate and zip
# The enumerate command provides the number associated to each item while zip makes a collection of pairs of items from two lists.
# In[115]:
for i, val in enumerate(['WV', 'BMW', 2016]):
print(val, "(item %d)" % i)
# In[116]:
for x, y in zip([1, 0, -1, 0], [0, 1, 0, -1]):
print("x =", x, ", y =", y)
# **Question**
#
# Produce the following output:
#
# BBC was launched in 1992.
# CNN was launched in 1980.
# FOX NEWS was launched in 1996.
# In[117]:
x = ['BBC', 'CNN', 'FOX NEWS']
y = [1992, 1980, 1996]
# In[ ]:
# Answer
# ### Making a list in a concise manner
# (also called *list comprehensions*)
# In[119]:
l = [a**2 for a in range(10)]
print(l)
# In[120]:
l = [a**2 for a in range(10) if a%2 == 0]
print(l)
# **Question**
#
# Build the list of square root values of items in $x$.
# In[121]:
x = [1.5, 41., .413, 5.13, 3.4, 8.74]
# In[ ]:
# Answer
# ## While loop
# Akin to the `for` statement, the `while` loop benefits from the keywords `break`, `continue` and `else`.
# In[123]:
v = 0
while v**2 < 10:
v += .01
else:
print("the loop was not broken")
print("sqrt(10) is approximately {0:.2f}".format(v-.01))
# **Question**
#
# Write a loop that finds the floor value of $x$.
# In[124]:
x = 12.3
# In[ ]:
# Answer
# ## Function
# A function is defined with the keyword `def`:
# In[126]:
def test():
"""Test function
This function prints \"This is a test\"
"""
print("This is a test")
test()
# The documentation string (or docstring) of the function appears when one uses *help* or *?*:
# In[127]:
get_ipython().run_line_magic('pinfo', 'test')
# Note that a function is an object like an integer or a list.
# In[128]:
type(test)
# In[129]:
f = test
f()
# Functions can also return a result:
# In[130]:
def add(a, b):
return a+b
print(add(1, 2))
# ### Parameters
# A function can have two kinds of parameters:
# - mandatory parameters;
# - optional parameters.
# Optional parameters always come after mandatory ones and are defined with default values.
# In the following example, *name* is mandatory, while *age* and *job* are optional.
# In[131]:
def identity(name, age=39, job="trader"):
print("My name is %s." % name)
print("I am a %s and I am %d years old." % (job, age))
print()
identity("Picasso", 40, "painter")
identity("Kerviel")
# In this example, the function is called with positional arguments.
# This means that the order of the parameters should be the same as in the definition.
# However, parameters can also be passed with their keyword.
# In this case, the order is not significant.
# In[132]:
identity(job="musician", name="Armstrong", age=42)
# When both techniques are mixed, positional arguments always come before keyword arguments.
# In[133]:
identity("Bach", job="composer")
# One can check if a parameter has been passed using the neutral value *None*:
# In[134]:
def init_f(a, b=None):
if b is None:
b = a + 1
return a, b
print(init_f(1, 3))
print(init_f(1))
# **Question**
#
# Write a function, called *sq*, that has two arguments: *x* and *gamma* (default value: 1) and that returns $gamma ~\times~ x^2$.
# In[ ]:
# Answer
# ### Packing and unpacking arguments
# Parameters can be packed in a tuple or a dictionary and unpacked when calling a function.
# In[136]:
tuple_arg = ("Diniz", 38, "race walker")
identity(*tuple_arg)
# In[137]:
dic_arg = {"job": "judoka", "age": 27, "name": "Riner"}
identity(**dic_arg)
# Respectively, a function can be defined with packed arguments.
# This makes it possible to allow an arbitrary number of arguments.
# In[138]:
def student(level="B1", *args, **kwargs):
identity(**kwargs)
print("I am also a student (level {}).".format(level))
print("I study ", end="")
for it in args[:-1]:
print(it, end=", ")
print("and ", args[-1], ".")
student("M2", "Statistics", "Machine learning", name="John", job="violonist", age=22)
# **Question**
#
# Write a function that prints the number of arguments and each of its arguments on a separate line.
# In[ ]:
# Answer
# ### Modifying parameters
# Like in other languages, a function can modifier some parameters.
# The rule is:
# - if an argument is mutable, then it can be modified inside a function;
# - if an argument is immutable, it cannot be modified.
# In[140]:
def repeat(*args):
for it in args:
it *= 2
a = (1, 2) # Immutable
b = [1, 2] # Mutable
repeat(a, b)
print(a, b)
# ### Lambda expressions
# A lambda function is a small anonymous function, that is restricted to a single expression.
# It is generally used as an argument to or an output from a usual function.
# In[141]:
def apply(x, fun=lambda x: x):
return [fun(item) for item in x]
def arithmetic_progression(a=0, b=1):
return lambda n: a + n*b
# In[142]:
f = arithmetic_progression(1, 2)
print(apply(range(10), f))
# **Question**
#
# Given the function $sq$ (created just before), define a lambda function that returns $4x^2$.
# In[ ]:
# Answer
# ### Methods
# Since Python is an object-oriented programming language, objects always come with functions linked to them.
# These functions are called *methods* and generally modify directly the variable they are called with.
# For instance:
# In[144]:
l = [1, 3, 5]
l.reverse() # l is reversed (thus modified)
print(l)
# To know the methods associated to an object (here the list `l`), write:
#
# l.
#
# then press TAB.
# To obtain an inline help concerning a method (here list.reverse), write:
#
# l.reverse
#
# then press SHIFT+TAB.
# **Question**
#
# Sort the previous list.
# In[ ]:
# Answer
# ## Modules
# ### Loading modules
# Up to now, we only experienced internal features of Python.
# Yet, our interest will next focus on external tools.
# These tools are stored in modules, which can be loaded in several manners.
# In[146]:
import sys # Load the sys module
import numpy as np # Load the numpy module with the name np
from scipy import stats # Load the stats submodule from the scipy module
from scipy.linalg import inv # Load the matrix inversion function from a submodule
from statsmodels import * # Import evrything from the statsmodels module
# The last manner is not recommended since it can create name clashes between modules and makes the code harder to read and to understand.
#
# To know the content of a module, use `dir`:
# In[147]:
dir(sys)[-10:]
# Now, modules content can be accessed in the following manner:
# In[148]:
print(np.pi)
# **Question**
#
# Compute $e^{-1}$.
# In[ ]:
# Answer
# ### Handling the path and creating modules
# To be found by Python, modules should be stored in a directory of *sys.path*:
# In[150]:
sys.path
# If your module is stored in another directory, add it to the Python path:
# In[151]:
sys.path.append('./aux/')
# Now, to create a module in the directory `./aux/`, store the functions and variables definitions (see cell below) in a Python file, named `my_module.py` (for example using Spyder).
# Then, you can write:
#
# %load aux/my_module.py
#
# to know the content of the file `aux/my_module.py`.
# In[152]:
# %load aux/my_module.py
"""
Test module.
Author: Maxime Sangnier
"""
def f1():
print("Function 1")
def f2():
print("Function 2")
pi = 3.14
if __name__ == "__main__":
f1() # Example of using this module
# In[153]:
import my_module as m
get_ipython().run_line_magic('pinfo', 'm')
# In[154]:
m.f2()
# In Python 2, if you modify your module, reload it this way:
#
# reload(m)
#
# otherwise changes won't be considered.
# The last part of the module is executed when `my_module.py` is run as a script:
# In[155]:
run aux/my_module.py
# # Exercises
# ## Exercise 1
#
# In order to practice Markdown and $\LaTeX$, create a separate notebook and try to reproduce the output provided below.
# Some remarks:
# - you have to use headings;
# - you have to write inline $\LaTeX$ formulas;
# - you have to produce centered $\LaTeX$ equations;
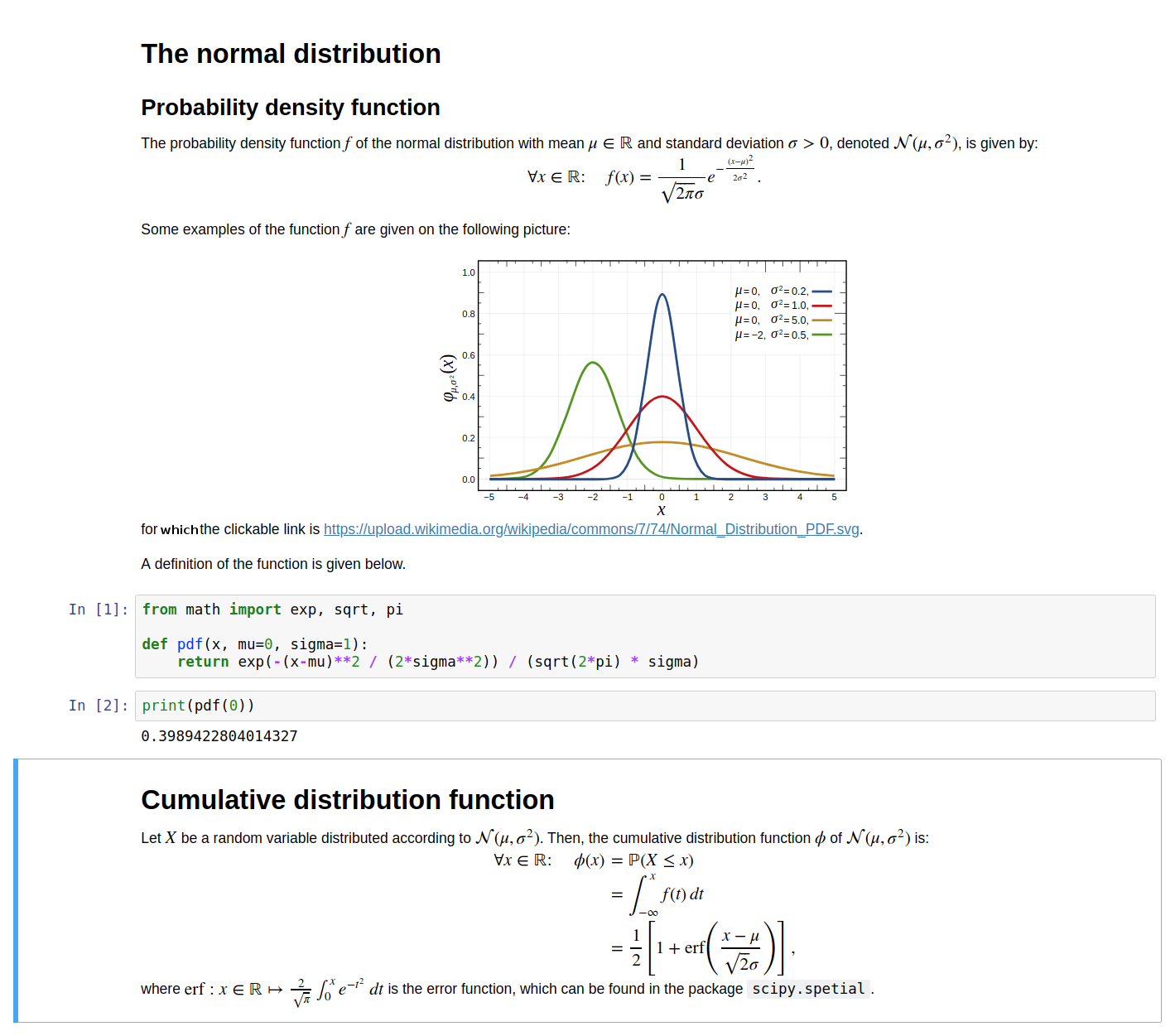
# - the image is inserted with its URL: [https://upload.wikimedia.org/wikipedia/commons/7/74/Normal_Distribution_PDF.svg](https://upload.wikimedia.org/wikipedia/commons/7/74/Normal_Distribution_PDF.svg);
# - you have to alternate Markdown and code cells;
# - you have to write centered and and aligned sequences of formulas in $\LaTeX$.
#
# Then, export your new notebook to an `html` file and send it to this [remote repository](https://www.dropbox.com/request/mJw1HxVjOkMSAqD5WHZD).
#
# The result to reproduce:
#
#
` to resize the image.
#
#
#
#
#
# References can be made to external links with `[text](URL)` and to internal labels with `[text](#label)`, where a tag `` has been put somewhere in the notebook.
#
# ### Equations
# Equations should be written in the $\LaTeX$ language, for which help is [available](https://fr.wikipedia.org/wiki/Aide:Formules_TeX).
# If you know the symbol and want to obtain the $\LaTeX$ command, you can [detexify](http://detexify.kirelabs.org/classify.html) it.
#
# You only need basics of $\LaTeX$:
# - Inline equation with `$equation$`: $x = \sqrt{2}$.
# - Centered equation with
#
#
# $$
# [equation]
# $$
#
# For instance:
# $$
# \int_0^1 1 \, dx = 1.
# $$
# - Multiple line equation with
#
#
# \begin{align}
# item &= item \\
# &= item.
# \end{align}
#
# For instance:
# \begin{align}
# \int_0^1 1 \, dx &= \frac{1}{2} \int_0^1 2 \, dx\\
# &= \frac{1}{2} \cdot 2 \\
# &= 1.
# \end{align}
# - Exponents and subscripts with `^` and `_`: $x_{i}^2$.
# - Summation and product with `\sum_{i=1}^n` and `\prod_{i=1}^n`: $\sum_{i=1}^n \prod_{j=1}^m x_{ij}$.
# - Real numbers with `\mathbb`: $\forall x \in \mathbb R^d$.
# - Calligraphic letters with `\mathcal`: $\mathcal N(0, 1)$.
# - Big parentheses with `\left(… \right)`: $\left( \frac{1}{n} \sum_{i=1}^n x_i \right)$.
# # Basics of the Python language
# ## Numbers
# ### Integer, floats and complex
# In[4]:
a = 1 # Integer
b = 1. # Float
c = 1.+2.j # Complex
# In[5]:
print(a)
type(a)
# In[6]:
print(b)
type(b)
# In[7]:
print(c)
type(c)
# In[8]:
print(c.real, c.imag)
# **Question**
#
# What are the result and the type of the following expressions:
# - 3+5.;
# - 16 * 4;
# - 8 / 2;
# - 2 * 10 / 2?
# In[ ]:
# Answer
# ### Booleans
# In[10]:
test = True
type(test)
# In[11]:
print(test and a == 1)
# In[12]:
print(test or a == 2)
# In[13]:
print(a != 1)
# In[14]:
print(test and not a == 1)
# A Boolean is a number:
# In[15]:
print(int(test)) # Cast Boolean to int
# In[16]:
print(test+1, test-1, test*3.2)
# **Question**
#
# Write an expression that returns:
# - $-1$ if $x \le -1$;
# - $1$ if $x \ge 1$;
# - x otherwise.
# In[ ]:
# Answer
# ### Swap variables in a concise manner
# In[18]:
abis = 3
print(a, abis)
a, abis = abis, a # Swap variables
print(a, abis)
# ### Operations
# Integers, floats, complex numbers and Booleans benefit from usual arithmetic operations.
#
# - Addition:
# In[19]:
print(a+2.3)
# - Subtraction:
# In[20]:
print(b-3)
# - Multiplication:
# In[21]:
print(c * 3)
# - Division:
# Beware: integers inherit from integer division in Python 2 and floating division in Python 3.
# In[22]:
print(1/2) # Returns 0 in Python 2 and 0.5 in Python 3
# A good practice is to use floating numbers:
# In[23]:
print(1./2)
print(a/2.)
# As well as explicit integer division (note that the result is of type *int*):
# In[24]:
a = 3//2
print(a, type(a))
# - Power:
# In[25]:
print(10**3)
# - Modulo:
# In[26]:
print(5%2)
# **Question**
#
# Given two integers $x$ and $y$ such that $x \ge y$, compute and print the quotient of the Euclidean division of $x$ by $y$.
# Do the same for the remainder (with two different expressions).
# In[ ]:
# Answer
# ## Data structures
# ### Strings
# Strings are immutable objects (they cannot be modified), that can be defined with simple, double or triple quotes.
# Simple and double quotes are equivalent:
# In[28]:
test1 = "Wilcoxon"
test2 = 'Chi2'
print(test1)
# … Except for quotes themselves.
# We write:
# In[29]:
print("\"" + " or " + '"')
# And:
# In[30]:
print('\'' + ' or ' + "'")
# Triple quotes allow to have several lines:
# In[31]:
txt1 = """This is
a Wilcoxon test"""
print(txt1)
# This is equivalent to using the special character *\\n*:
# In[32]:
txt2 = "This is\na Chi2 test"
print(txt2)
# #### Operations on strings
# Strings can be concatenated and repeated.
# In[33]:
print(test1 + ", p=" + str(0.1)) # Concatenation
print(test2 * 3) # Repetition
# We can change the case of a string.
# In[34]:
print(test1.lower())
print(test2.upper())
print("mr. ".capitalize() + "tickle".capitalize())
# Strings can be joined with a given separator.
# In[35]:
"-".join([test1, test2])
# **Question**
#
# Given the three variables below, produce the string:
#
# outcome ~ xx + yy + zz
# In[36]:
x = "Xx"
y = "YY"
z = "zZ"
# In[ ]:
# Answer
# #### String formatting and printing
# Python 3 provides an improved string formatting syntax, called f-string.
# In a nutshell, it is enough to put an *f* at the beginning and curly braces around expressions that should be replaced with their values.
# In[38]:
print(f"The first test is {test1}, while the second is {test2}.")
# Multiline f-strings are allowed:
# In[39]:
pval = 0.03
(f"The p-value for the {test1} test is: "
f"{pval}")
# Or escaping a return with *\*:
# In[40]:
f"The p-value for the {test1} test is: " \
f"{pval}"
# Using triple " will lead to:
# In[41]:
print(f"""The p-value for the {test1} test is:
{pval}""")
# Format specifiers: `{value:{width}.{precision}}` can be used, mainly for numbers:
# In[42]:
root = 0.123456789
print(f"The root is {root:.3f}.")
print(f"The root is {root:.2e}.")
print(f"The root is {root:10.2f}.")
# For a full support, see the [Format Specification Mini-Language](https://docs.python.org/3.6/library/string.html#formatspec).
# Strings can also be formatted in the old way:
# In[43]:
print("The first test is {}, while the second is {}.".format(test1, test2)) # With positional arguments
print("The first test is {1}, while the second is {0}.".format(test1, test2)) # With numbered arguments
print("The first test is {T1}, while the second is {T2}."
.format(T1=test1, T2=test2)) # With keywords arguments
print("The first test is {}, while the second is {T2}."
.format(test1, T2=test2))
print("The root is {}.".format(0.123456789)) # Numbers can be printed directly or converted
print("The root is {0:.3f}.".format(0.123456789))
print("The root is {0:.2e}.".format(0.123456789))
print("The root is {0:10.2f}.".format(0.123456789))
# In the expression *x:y.zA*,
# - *x* is the positioning parameter;
# - *y* is the (minimum) number of (potentially blank) numbers before .;
# - *z* is the (maximum) number of numbers after .;
# - *A* is the formatting letter:
# - f: float;
# - e: exponential notation;
# - d: integer.
# Strings can also be formatted in the very old way:
# In[44]:
print("An integer: %d" % 2)
print("A float: %f" % 0.123456789)
print("A short float: %0.2f" % 0.123456789)
print("A nice p-value: %0.1e" % 0.05)
print("%s is %d years old" % ("Robert", 64))
# When several arguments are given, *print* prints them all (the behavior is slightly different between Python 2 and Python 3).
# In[45]:
print("string 1", "string 2")
# One can also control the end character:
# In[46]:
print("Something to say", end="") # Python 3
#print("Something to say"), # Python 2
print("… and something else")
# **Remark:** objects can be printed simply by evaluating them:
# In[47]:
test1
# To remove this side effect, use a semicolon:
# In[48]:
test1;
# **Question**
#
# Given the three variables below, produce the sentence:
#
# The expression x+y*z = 3+1.4142*5 approximately equals 1.01e+01.
# In[49]:
x = 3
y = 2**0.5
z = 5
# In[ ]:
# Answer
# ### List
# A list is an ordered collection of items, that may have different types.
# A list is a mutable object and can thus be modified.
# In[51]:
l = [1, 3, 5, 7, "odd numbers"]
print(l)
# #### Indexing and slicing
# Indexing starts at 0.
# In[52]:
print("First item: ", l[0]) # First item
print("Last item: ", l[-1]) # Last item
# The slicing syntax is: `l[start:stop:stride]`.
# If some arguments are omitted, they are replaced by the *natural* ones (`start=0`, `stride=1`).
# In[53]:
print("First two items: ", l[:2]) # Equivalent to l[0:2]
print("Sublists: ", l[::2], l[1:3]) # First sublist equivalent to l[0::2]
print("Reverse: ", l[::-1])
# Note that, when slicing, the last element is not considered.
# In[54]:
print(l[0:2]) # Items numbered 0 and 1 (2 excluded)
print(l[2:]) # All items after number 2 included
print(l[2:-1]) # All items after number 2 included, last item exluced
# **Question**
#
# Given the list below (of size denoted by $n$), print its head (the first $n-1$ items) and its tail (the last $n-1$ items).
# In[55]:
x = [5, 3, 7, 8, 3, 4, 6]
# In[ ]:
# Answer
# #### Concatenation, extension and repetition
# In[57]:
l = l+[9] # Concatenation
print(l)
# In[58]:
l += [11] # Concatenation
print(l)
# Extension is an in-place operation.
# In[59]:
l.extend(["extension"]) # Extension
print(l)
# In[60]:
l *= 2 # Repetition
print(l)
# #### Adding, deleting and indexing an item
# In[61]:
l.append(13) # Add an item at the end of the list
print(l)
# In[62]:
del l[0] # Delete the first item
print(l)
# In[63]:
print("9 is in position", l.index(9))
# **Question**
#
# Move the first item of $x$ to the last position.
# In[64]:
x = [5, 3, 7, 8, 3, 4, 6]
# In[ ]:
# Answer
# #### Presence
# In[66]:
print("2 is in l: ", 2 in l)
print("3 is in l: ", 3 in l)
# #### Other operations
# In[67]:
print(len(l))
# In[68]:
l.reverse()
print(l)
# More details: use *help(list)* or *list?* in Ipython and Jupyter notebook.
# ### Tuple
# Roughly speaking, a tuple is an immutable list (it cannot be changed).
# It can be defined in two ways:
# In[69]:
t = (1, 2) # Definition with parentheses
type(t)
# In[70]:
t = 1, 2 # Light definition
print(t)
# In[71]:
t += ("three",) # Concatenation with a singleton
print(t)
print("Length: ", len(t)) # Length
# In[72]:
t0, t1, t2 = t # Unpacking
print(t0, t1, t2)
# ### Sets
# A set is an unordered collection of unique items.
# Usual mathematical operations (union, difference) can be performed.
# In[73]:
odd = set([1, 3, 5, 5])
even = set([2, 4])
type(odd)
print(odd)
# In[74]:
print(odd - set([1])) # Difference of sets
# In[75]:
print(odd | even) # Union of sets
# In[76]:
odd.add(2)
print(odd & even) # Intersection of sets
# In[77]:
print(odd ^ even) # Complementary of the intersection of sets
# **Question**
#
# Print items that are simultaneously in $x$ and $y$.
# In[78]:
x = [5, 3, 7, 8, 3, 4, 6]
y = [1, 9, 3, 7, 6, 2]
# In[ ]:
# Answer
# ### Dictionary
# A dictionary is a table key/value.
# Keys can be any immutable type (string, numbers, …).
# In[80]:
d = {'x': [[1, -0.5], [-2, 1]], 'y': [0, 1]} # Definition
print(d['x'])
# In[81]:
d[10] = "ten" # Add an item
print(d)
# In[82]:
# Print keys and values
print(d.keys())
print(d.values())
# In[83]:
"x" in d # Check if a key is in the dictionary
# **Question**
#
# Add a new item to the dictionary defined below, with key "sigma2" and value $sigma^2$.
# Set $mu$ to $0$ and print the final dictionary.
# In[84]:
db = {'mu': 3, 'sigma': 1.5}
# In[ ]:
# Answer
# ### Assignment operator
# In Python the assignment operator `=` is used for two purposes:
# - modifying attributes and items of mutable objects;
# - binding a name to a value.
#
# The last point means that **`=` does not make a copy** but creates a new alias for an already existing value.
#
# Examples:
# - Immutable objects:
# In[86]:
a = 1.1
b = a
b is a # two names, same data (in memory)
# In[87]:
print(id(a), id(b))
# In[88]:
a = "monday"
b = a
b is a # two names, same data (in memory)
# In[89]:
a = 3, 10
b = a
b is a # two names, same data (in memory)
# - Mutable objects:
# In[90]:
a = [1, 2]
b = a
b is a # two names, same data (in memory)
# In[91]:
b[-1] = 3
print(a)
print(b)
# Modifications appear on both a and b (same data).
# To make a copy, use:
# In[92]:
b = a.copy() # In Python 3
#b = a[:] # In Python 2
b is a
# In[93]:
b[-1] = 2
print(a)
print(b)
# *a* and *b* are two different objects.
#
# This is the same for dictionaries and sets:
# In[94]:
a = {"k": 1}
b = a
b is a
# In[95]:
b = a.copy()
b is a
# In[96]:
a = set([1, 2])
b = a
b is a
# In[97]:
b = a.copy()
b is a
# ## Conditional statements
# In Python, the blocks of the control flows are delimited by indentation.
# See for instance the use of `if/elif/else` statement.
# The comparisons are made with `==`, `!=`, `is`, `in`, `not`, `<`, `<=`, …
# In[98]:
h = 3.14 # Target
i = 3 # Guess
print("The target is", end=" ")
if h < i:
print("less than %d." % i)
elif h > i:
print("greater than %d." % i)
else:
print("exactly %d." % i)
# **Question**
#
# Write a conditional statement that:
# - add y to x if y is missing in x;
# - change y to -y in x otherwise.
# In[99]:
x = [4, 2, 7]
y = 6
# In[ ]:
# Answer
# ### Evaluating objects
# `if [object]` is false for
# - 0, 0.0 numbers;
# - empty structures;
# - False and None;
#
# and true otherwise.
#
# **Example**: checking if a list is empty.
# In[101]:
a = []
if not a:
print("Empty list.")
# **Question**
#
# Write a script that prints the result of the operation $x/y$ if $y \neq 0$ and "infinity" otherwise.
# In[ ]:
# Answer
# ### Assignment operator
# Conditional statements can also be used in union with the assignment operator:
# In[104]:
res = "greater or equal" if h >= i else "less"
print("The target is " + res + " than %d." % i)
# ## For loop
# Example of a for loop:
# In[105]:
for it in range(10):
print(it, end=" ")
else:
print("\nthe loop was not broken")
# Here, the optional `else` part is executed when the loop goes until the end.
# If the loop is broken (such as in the following example), the `else` part is not executed.
# Besides `break`, another interested keyword is `continue`. It skips the end of the current iteration.
# In[106]:
for it in range(10):
if it % 2 == 0: # Even numbers
continue
if it > 8:
break
print(it, end=" ")
else:
print("\nthe loop was not broken")
# A special feature of Python is to being able to iterate over the items of any sequence (range, list, tuple, dictionary, …).
#
# ### Range
# The syntax for the range function is:
# `range(stop)` or `rang(start, stop, step)` with third parameter optional.
# In[107]:
for it in range(5):
print(it, end=" ")
# In[108]:
for it in range(10, 20, 3):
print(it, end=" ")
# ### List
# In[109]:
for car in ['WV', 'BMW', 2016]:
print(car)
# ### Tuple
# In[110]:
for it in ("My favorite number", "is", 7):
print(it, end=" ")
# ### Dictionary
# In[111]:
conf = {"Name": "NIPS", "Date": 2016, "Location": "Barcelona"}
for key in conf:
print(key)
# In[112]:
for key, value in conf.items():
print(key, ":", value)
# In[113]:
for key, value in sorted(conf.items()):
print(key, ":", value)
# **Question**
#
# Compute and print the first 10 items of the sequence
# $$
# \begin{cases}
# u_0 &=& 0 \\
# u_{n+1} &=& 3u_n+2, \forall n \in \mathbb N.
# \end{cases}
# $$
# In[ ]:
# Answer
# ### Useful commands: enumerate and zip
# The enumerate command provides the number associated to each item while zip makes a collection of pairs of items from two lists.
# In[115]:
for i, val in enumerate(['WV', 'BMW', 2016]):
print(val, "(item %d)" % i)
# In[116]:
for x, y in zip([1, 0, -1, 0], [0, 1, 0, -1]):
print("x =", x, ", y =", y)
# **Question**
#
# Produce the following output:
#
# BBC was launched in 1992.
# CNN was launched in 1980.
# FOX NEWS was launched in 1996.
# In[117]:
x = ['BBC', 'CNN', 'FOX NEWS']
y = [1992, 1980, 1996]
# In[ ]:
# Answer
# ### Making a list in a concise manner
# (also called *list comprehensions*)
# In[119]:
l = [a**2 for a in range(10)]
print(l)
# In[120]:
l = [a**2 for a in range(10) if a%2 == 0]
print(l)
# **Question**
#
# Build the list of square root values of items in $x$.
# In[121]:
x = [1.5, 41., .413, 5.13, 3.4, 8.74]
# In[ ]:
# Answer
# ## While loop
# Akin to the `for` statement, the `while` loop benefits from the keywords `break`, `continue` and `else`.
# In[123]:
v = 0
while v**2 < 10:
v += .01
else:
print("the loop was not broken")
print("sqrt(10) is approximately {0:.2f}".format(v-.01))
# **Question**
#
# Write a loop that finds the floor value of $x$.
# In[124]:
x = 12.3
# In[ ]:
# Answer
# ## Function
# A function is defined with the keyword `def`:
# In[126]:
def test():
"""Test function
This function prints \"This is a test\"
"""
print("This is a test")
test()
# The documentation string (or docstring) of the function appears when one uses *help* or *?*:
# In[127]:
get_ipython().run_line_magic('pinfo', 'test')
# Note that a function is an object like an integer or a list.
# In[128]:
type(test)
# In[129]:
f = test
f()
# Functions can also return a result:
# In[130]:
def add(a, b):
return a+b
print(add(1, 2))
# ### Parameters
# A function can have two kinds of parameters:
# - mandatory parameters;
# - optional parameters.
# Optional parameters always come after mandatory ones and are defined with default values.
# In the following example, *name* is mandatory, while *age* and *job* are optional.
# In[131]:
def identity(name, age=39, job="trader"):
print("My name is %s." % name)
print("I am a %s and I am %d years old." % (job, age))
print()
identity("Picasso", 40, "painter")
identity("Kerviel")
# In this example, the function is called with positional arguments.
# This means that the order of the parameters should be the same as in the definition.
# However, parameters can also be passed with their keyword.
# In this case, the order is not significant.
# In[132]:
identity(job="musician", name="Armstrong", age=42)
# When both techniques are mixed, positional arguments always come before keyword arguments.
# In[133]:
identity("Bach", job="composer")
# One can check if a parameter has been passed using the neutral value *None*:
# In[134]:
def init_f(a, b=None):
if b is None:
b = a + 1
return a, b
print(init_f(1, 3))
print(init_f(1))
# **Question**
#
# Write a function, called *sq*, that has two arguments: *x* and *gamma* (default value: 1) and that returns $gamma ~\times~ x^2$.
# In[ ]:
# Answer
# ### Packing and unpacking arguments
# Parameters can be packed in a tuple or a dictionary and unpacked when calling a function.
# In[136]:
tuple_arg = ("Diniz", 38, "race walker")
identity(*tuple_arg)
# In[137]:
dic_arg = {"job": "judoka", "age": 27, "name": "Riner"}
identity(**dic_arg)
# Respectively, a function can be defined with packed arguments.
# This makes it possible to allow an arbitrary number of arguments.
# In[138]:
def student(level="B1", *args, **kwargs):
identity(**kwargs)
print("I am also a student (level {}).".format(level))
print("I study ", end="")
for it in args[:-1]:
print(it, end=", ")
print("and ", args[-1], ".")
student("M2", "Statistics", "Machine learning", name="John", job="violonist", age=22)
# **Question**
#
# Write a function that prints the number of arguments and each of its arguments on a separate line.
# In[ ]:
# Answer
# ### Modifying parameters
# Like in other languages, a function can modifier some parameters.
# The rule is:
# - if an argument is mutable, then it can be modified inside a function;
# - if an argument is immutable, it cannot be modified.
# In[140]:
def repeat(*args):
for it in args:
it *= 2
a = (1, 2) # Immutable
b = [1, 2] # Mutable
repeat(a, b)
print(a, b)
# ### Lambda expressions
# A lambda function is a small anonymous function, that is restricted to a single expression.
# It is generally used as an argument to or an output from a usual function.
# In[141]:
def apply(x, fun=lambda x: x):
return [fun(item) for item in x]
def arithmetic_progression(a=0, b=1):
return lambda n: a + n*b
# In[142]:
f = arithmetic_progression(1, 2)
print(apply(range(10), f))
# **Question**
#
# Given the function $sq$ (created just before), define a lambda function that returns $4x^2$.
# In[ ]:
# Answer
# ### Methods
# Since Python is an object-oriented programming language, objects always come with functions linked to them.
# These functions are called *methods* and generally modify directly the variable they are called with.
# For instance:
# In[144]:
l = [1, 3, 5]
l.reverse() # l is reversed (thus modified)
print(l)
# To know the methods associated to an object (here the list `l`), write:
#
# l.
#
# then press TAB.
# To obtain an inline help concerning a method (here list.reverse), write:
#
# l.reverse
#
# then press SHIFT+TAB.
# **Question**
#
# Sort the previous list.
# In[ ]:
# Answer
# ## Modules
# ### Loading modules
# Up to now, we only experienced internal features of Python.
# Yet, our interest will next focus on external tools.
# These tools are stored in modules, which can be loaded in several manners.
# In[146]:
import sys # Load the sys module
import numpy as np # Load the numpy module with the name np
from scipy import stats # Load the stats submodule from the scipy module
from scipy.linalg import inv # Load the matrix inversion function from a submodule
from statsmodels import * # Import evrything from the statsmodels module
# The last manner is not recommended since it can create name clashes between modules and makes the code harder to read and to understand.
#
# To know the content of a module, use `dir`:
# In[147]:
dir(sys)[-10:]
# Now, modules content can be accessed in the following manner:
# In[148]:
print(np.pi)
# **Question**
#
# Compute $e^{-1}$.
# In[ ]:
# Answer
# ### Handling the path and creating modules
# To be found by Python, modules should be stored in a directory of *sys.path*:
# In[150]:
sys.path
# If your module is stored in another directory, add it to the Python path:
# In[151]:
sys.path.append('./aux/')
# Now, to create a module in the directory `./aux/`, store the functions and variables definitions (see cell below) in a Python file, named `my_module.py` (for example using Spyder).
# Then, you can write:
#
# %load aux/my_module.py
#
# to know the content of the file `aux/my_module.py`.
# In[152]:
# %load aux/my_module.py
"""
Test module.
Author: Maxime Sangnier
"""
def f1():
print("Function 1")
def f2():
print("Function 2")
pi = 3.14
if __name__ == "__main__":
f1() # Example of using this module
# In[153]:
import my_module as m
get_ipython().run_line_magic('pinfo', 'm')
# In[154]:
m.f2()
# In Python 2, if you modify your module, reload it this way:
#
# reload(m)
#
# otherwise changes won't be considered.
# The last part of the module is executed when `my_module.py` is run as a script:
# In[155]:
run aux/my_module.py
# # Exercises
# ## Exercise 1
#
# In order to practice Markdown and $\LaTeX$, create a separate notebook and try to reproduce the output provided below.
# Some remarks:
# - you have to use headings;
# - you have to write inline $\LaTeX$ formulas;
# - you have to produce centered $\LaTeX$ equations;
# - the image is inserted with its URL: [https://upload.wikimedia.org/wikipedia/commons/7/74/Normal_Distribution_PDF.svg](https://upload.wikimedia.org/wikipedia/commons/7/74/Normal_Distribution_PDF.svg);
# - you have to alternate Markdown and code cells;
# - you have to write centered and and aligned sequences of formulas in $\LaTeX$.
#
# Then, export your new notebook to an `html` file and send it to this [remote repository](https://www.dropbox.com/request/mJw1HxVjOkMSAqD5WHZD).
#
# The result to reproduce:
#
#  #
# ## Exercise 2
# Create the following list with loops:
#
# [['car', 0, 1, 4, 9, 16],
# ['bus', 1, 4, 9, 16, 25],
# ['train', 4, 9, 16, 25, 36]]
#
# In[ ]:
# Answer
# Create a script that prints this list in the following manner:
#
# car 0 1 4 9 16
# bus 1 4 9 16 25
# train 4 9 16 25 36
#
# In[ ]:
# Answer
# ## Exercise 3
# Create a function that returns the sum log of all its parameters (use the `log` function from the `math` module).
#
# In[ ]:
# Answer
# ## Exercise 4
# For the following list of dictionaries, write a script that adds a field `registrations` which is twice the number of accepted papers.
# In[160]:
confs = [{"Name": "NIPS", "Date": 2016, "Location": "Barcelona", "acc_papers": 300},
{"Name": "ICML", "Date": 2016, "Location": "New York City", "acc_papers": 450},
{"Name": "ICML", "Date": 2015, "Location": "Lille", "acc_papers": 250},
{"Name": "AISTATS", "Date": 2016, "Location": "Cadiz", "acc_papers": 100}]
# In[ ]:
# Answer
# ## Exercise 5
# Write a function `append`, that produces the following results:
#
# l = [1]
# append(l, 5)
# print(l)
# [1, 5]
# append(l, "-1")
# print(l)
# [1, 5, '-1']
# append(l)
# print(l)
# []
#
# In[ ]:
# Answer
# ## Exercise 6
# With the code editor, create a module, that contains two functions:
# - fibonacci(n): computes the $n^{th}$ [Fibonacci number](https://en.wikipedia.org/wiki/Fibonacci_number);
# - wallis(n): computes an approximation of $\pi$ using the [Wallis product](https://en.wikipedia.org/wiki/Wallis_product).
#
# Write a script, that uses these two functions.
# In[ ]:
# Answer
# # References
# - [JupyterLab documentation](https://jupyterlab.readthedocs.io/en/latest/index.html).
# - [Official documentation](https://docs.python.org/3/tutorial/index.html).
# - [Scipy lecture notes](http://www.scipy-lectures.org/index.html).
# - [Allen Downey's book](http://www.greenteapress.com/thinkpython/thinkpython.pdf).
#
# ## Exercise 2
# Create the following list with loops:
#
# [['car', 0, 1, 4, 9, 16],
# ['bus', 1, 4, 9, 16, 25],
# ['train', 4, 9, 16, 25, 36]]
#
# In[ ]:
# Answer
# Create a script that prints this list in the following manner:
#
# car 0 1 4 9 16
# bus 1 4 9 16 25
# train 4 9 16 25 36
#
# In[ ]:
# Answer
# ## Exercise 3
# Create a function that returns the sum log of all its parameters (use the `log` function from the `math` module).
#
# In[ ]:
# Answer
# ## Exercise 4
# For the following list of dictionaries, write a script that adds a field `registrations` which is twice the number of accepted papers.
# In[160]:
confs = [{"Name": "NIPS", "Date": 2016, "Location": "Barcelona", "acc_papers": 300},
{"Name": "ICML", "Date": 2016, "Location": "New York City", "acc_papers": 450},
{"Name": "ICML", "Date": 2015, "Location": "Lille", "acc_papers": 250},
{"Name": "AISTATS", "Date": 2016, "Location": "Cadiz", "acc_papers": 100}]
# In[ ]:
# Answer
# ## Exercise 5
# Write a function `append`, that produces the following results:
#
# l = [1]
# append(l, 5)
# print(l)
# [1, 5]
# append(l, "-1")
# print(l)
# [1, 5, '-1']
# append(l)
# print(l)
# []
#
# In[ ]:
# Answer
# ## Exercise 6
# With the code editor, create a module, that contains two functions:
# - fibonacci(n): computes the $n^{th}$ [Fibonacci number](https://en.wikipedia.org/wiki/Fibonacci_number);
# - wallis(n): computes an approximation of $\pi$ using the [Wallis product](https://en.wikipedia.org/wiki/Wallis_product).
#
# Write a script, that uses these two functions.
# In[ ]:
# Answer
# # References
# - [JupyterLab documentation](https://jupyterlab.readthedocs.io/en/latest/index.html).
# - [Official documentation](https://docs.python.org/3/tutorial/index.html).
# - [Scipy lecture notes](http://www.scipy-lectures.org/index.html).
# - [Allen Downey's book](http://www.greenteapress.com/thinkpython/thinkpython.pdf).
 #
# Press CTRL+D or type:
#
# quit()
#
# to exit.
#
# If your code is written in a file *script.py*, you can run it from a shell with:
#
# python3 script.py
#
# or in Python with:
#
# execfile('script.py')
#
# ### IPython
# [IPython](http://ipython.org/) is a powerful interactive shell that comes with numerous useful features such as:
# - interactivity;
# - tab-completion;
# - command history;
# - object introspection;
# - special (magic) commands;
# - numbered input/output.
#
#
#
# Press CTRL+D or type:
#
# quit()
#
# to exit.
#
# If your code is written in a file *script.py*, you can run it from a shell with:
#
# python3 script.py
#
# or in Python with:
#
# execfile('script.py')
#
# ### IPython
# [IPython](http://ipython.org/) is a powerful interactive shell that comes with numerous useful features such as:
# - interactivity;
# - tab-completion;
# - command history;
# - object introspection;
# - special (magic) commands;
# - numbered input/output.
#
#  # In particular feature, it enables to run only part of the script while keeping the previous results (variable states) in memory.
#
# To run a script, you can edit it and press F5.
# If you want to execute only a selection of it, select the part of interest and press F9.
#
# ### JupyterLab
# JupyterLab is a novel web-based IDE to produce easy-to-read reports with text, equations, code and results (called a notebook).
# This is what is used here!
#
#
# In particular feature, it enables to run only part of the script while keeping the previous results (variable states) in memory.
#
# To run a script, you can edit it and press F5.
# If you want to execute only a selection of it, select the part of interest and press F9.
#
# ### JupyterLab
# JupyterLab is a novel web-based IDE to produce easy-to-read reports with text, equations, code and results (called a notebook).
# This is what is used here!
#
#  #
# To launch it, write in a shell:
#
# jupyter-lab
#
# ## Getting help
# Python and related modules are very well documented in local (docstrings) and on the Internet (documentation on the Internet may be clearer and updated compared to the local one).
# To access the docstring, use *help*:
# In[1]:
help(print)
# In a notebook (or IPython), you can also use *?*:
# In[2]:
get_ipython().run_line_magic('pinfo', 'print')
# or SHIFT+TAB:
#
#
#
# To launch it, write in a shell:
#
# jupyter-lab
#
# ## Getting help
# Python and related modules are very well documented in local (docstrings) and on the Internet (documentation on the Internet may be clearer and updated compared to the local one).
# To access the docstring, use *help*:
# In[1]:
help(print)
# In a notebook (or IPython), you can also use *?*:
# In[2]:
get_ipython().run_line_magic('pinfo', 'print')
# or SHIFT+TAB:
#
#  # Otherwise, you can search the net for an answer.
# The easiest way is to google your query: [vandermonde matrix python](https://www.google.fr/?client=ubuntu#channel=fs&q=vandermonde+matrix+python&gfe_rd=cr).
#
# Finally, you can go directly to a package documentation website.
# The following links provide the documentation of the packages used in this introduction (see next sections for details on the packages):
# - [official documentation](https://docs.python.org/3.5/tutorial/index.html);
# - [Scipy](http://docs.scipy.org/doc/scipy/reference/);
# - [Numpy](http://docs.scipy.org/doc/numpy/reference/);
# - [Statsmodels](http://www.statsmodels.org/stable/index.html);
# - [Scikit-learn](http://scikit-learn.org/stable/documentation.html).
#
# # An introduction to JupyterLab
# A notebook is a sequence of cells that may be of two types:
# - code: it enables to edit, execute and see the output of a small Python script;
# - markdown: if offers a way to write text and equations, as well as to import images.
#
# ## Survival kit
# A Jupyter notebook can be modified in two modes:
# - the command mode: we can add, delete and modify cells;
# - the edit mode: we can edit and run the script inside a cell.
#
# The forthcoming sections describe the most useful keyboard shortcuts.
# An exhaustive list of the available actions and shortcuts can be found by hitting the palette in the menu bar (or CTRL+SHIFT+C).
#
# It is highly recommended to experience these shortcuts on your own on the test cell below.
#
# ### Command shortcuts
# If you are in the edit mode, press ESC to enter the command mode.
#
# - To edit a cell (enter the edit mode), go to the desired cell and press ENTER.
# - To add a cell below, press B.
# - To add a cell above, press A.
# - To cut a cell, press X.
# - To copy a cell, press C.
# - To paste a cell below, press V.
# - To delete a cell, press DD.
# - To convert a cell to a markdown cell, press M.
# - To convert a cell to a code cell, press Y.
#
# ### Edit shortcuts
# If you are in the command mode, press ENTER to enter the edit mode.
#
# - To run a cell, press CTRL+ENTER.
# - To run a cell and select the one below, press SHIFT+ENTER.
# - To run a cell and add one below, press ALT+ENTER.
# - To apply autocompletion, press TAB at the end of the word. For example, write "pri", then press TAB.
# It gives "print".
# - To get an inline help, press SHIFT+TAB.
# - To indent several lines, select them and press TAB.
# - To dedent several lines, select them and press SHIFT+TAB.
# - To (un)comment a line (or several ones after selection), press CTRL+/.
# - To exit the edit mode, press ESC.
#
# In[3]:
print("This is a test cell")
# ## Useful features
# ### Code console
# You can open a code console by clicking the + button in the file browser and selecting the kernel.
# It enables you to run interactively small part of codes in a console, keeping the history in full view.
#
# Such a code console can also be opened or linked to a Python file.
# This is a way to run a part of code directly from a Python file.
# To do so, when editing this file, right-click in it and select *Create Console for Editor*. Then, select a single line or a block of code and send it to the code console by hitting SHIFT+ENTER.
#
# ### Mirrored output
# You can create a new synchronized view of a cell output by right-clicking a cell and hitting *Create New View for Output*.
# This view can then be moved to a separate tab.
# ## Text and equations
# By default, cells are for code but they can be converted to markdown cells (see the shortcut above).
# Markdown cells accept both [Markdown](https://jupyter-notebook.readthedocs.io/en/stable/examples/Notebook/Working%20With%20Markdown%20Cells.html) (text formatting) and [$\LaTeX$](https://fr.wikipedia.org/wiki/Aide:Formules_TeX) (equations).
#
# ### General formatting
# Headings are defined with the symbol `#`:
#
# # First level
# ## Second level
# ### Third level
# #### Fourth level
# ##### Fifth level
#
# Even though paragraphs are defined automatically, you can force a line break with the code `
# Otherwise, you can search the net for an answer.
# The easiest way is to google your query: [vandermonde matrix python](https://www.google.fr/?client=ubuntu#channel=fs&q=vandermonde+matrix+python&gfe_rd=cr).
#
# Finally, you can go directly to a package documentation website.
# The following links provide the documentation of the packages used in this introduction (see next sections for details on the packages):
# - [official documentation](https://docs.python.org/3.5/tutorial/index.html);
# - [Scipy](http://docs.scipy.org/doc/scipy/reference/);
# - [Numpy](http://docs.scipy.org/doc/numpy/reference/);
# - [Statsmodels](http://www.statsmodels.org/stable/index.html);
# - [Scikit-learn](http://scikit-learn.org/stable/documentation.html).
#
# # An introduction to JupyterLab
# A notebook is a sequence of cells that may be of two types:
# - code: it enables to edit, execute and see the output of a small Python script;
# - markdown: if offers a way to write text and equations, as well as to import images.
#
# ## Survival kit
# A Jupyter notebook can be modified in two modes:
# - the command mode: we can add, delete and modify cells;
# - the edit mode: we can edit and run the script inside a cell.
#
# The forthcoming sections describe the most useful keyboard shortcuts.
# An exhaustive list of the available actions and shortcuts can be found by hitting the palette in the menu bar (or CTRL+SHIFT+C).
#
# It is highly recommended to experience these shortcuts on your own on the test cell below.
#
# ### Command shortcuts
# If you are in the edit mode, press ESC to enter the command mode.
#
# - To edit a cell (enter the edit mode), go to the desired cell and press ENTER.
# - To add a cell below, press B.
# - To add a cell above, press A.
# - To cut a cell, press X.
# - To copy a cell, press C.
# - To paste a cell below, press V.
# - To delete a cell, press DD.
# - To convert a cell to a markdown cell, press M.
# - To convert a cell to a code cell, press Y.
#
# ### Edit shortcuts
# If you are in the command mode, press ENTER to enter the edit mode.
#
# - To run a cell, press CTRL+ENTER.
# - To run a cell and select the one below, press SHIFT+ENTER.
# - To run a cell and add one below, press ALT+ENTER.
# - To apply autocompletion, press TAB at the end of the word. For example, write "pri", then press TAB.
# It gives "print".
# - To get an inline help, press SHIFT+TAB.
# - To indent several lines, select them and press TAB.
# - To dedent several lines, select them and press SHIFT+TAB.
# - To (un)comment a line (or several ones after selection), press CTRL+/.
# - To exit the edit mode, press ESC.
#
# In[3]:
print("This is a test cell")
# ## Useful features
# ### Code console
# You can open a code console by clicking the + button in the file browser and selecting the kernel.
# It enables you to run interactively small part of codes in a console, keeping the history in full view.
#
# Such a code console can also be opened or linked to a Python file.
# This is a way to run a part of code directly from a Python file.
# To do so, when editing this file, right-click in it and select *Create Console for Editor*. Then, select a single line or a block of code and send it to the code console by hitting SHIFT+ENTER.
#
# ### Mirrored output
# You can create a new synchronized view of a cell output by right-clicking a cell and hitting *Create New View for Output*.
# This view can then be moved to a separate tab.
# ## Text and equations
# By default, cells are for code but they can be converted to markdown cells (see the shortcut above).
# Markdown cells accept both [Markdown](https://jupyter-notebook.readthedocs.io/en/stable/examples/Notebook/Working%20With%20Markdown%20Cells.html) (text formatting) and [$\LaTeX$](https://fr.wikipedia.org/wiki/Aide:Formules_TeX) (equations).
#
# ### General formatting
# Headings are defined with the symbol `#`:
#
# # First level
# ## Second level
# ### Third level
# #### Fourth level
# ##### Fifth level
#
# Even though paragraphs are defined automatically, you can force a line break with the code ` #
# ## Exercise 2
# Create the following list with loops:
#
# [['car', 0, 1, 4, 9, 16],
# ['bus', 1, 4, 9, 16, 25],
# ['train', 4, 9, 16, 25, 36]]
#
# In[ ]:
# Answer
# Create a script that prints this list in the following manner:
#
# car 0 1 4 9 16
# bus 1 4 9 16 25
# train 4 9 16 25 36
#
# In[ ]:
# Answer
# ## Exercise 3
# Create a function that returns the sum log of all its parameters (use the `log` function from the `math` module).
#
# In[ ]:
# Answer
# ## Exercise 4
# For the following list of dictionaries, write a script that adds a field `registrations` which is twice the number of accepted papers.
# In[160]:
confs = [{"Name": "NIPS", "Date": 2016, "Location": "Barcelona", "acc_papers": 300},
{"Name": "ICML", "Date": 2016, "Location": "New York City", "acc_papers": 450},
{"Name": "ICML", "Date": 2015, "Location": "Lille", "acc_papers": 250},
{"Name": "AISTATS", "Date": 2016, "Location": "Cadiz", "acc_papers": 100}]
# In[ ]:
# Answer
# ## Exercise 5
# Write a function `append`, that produces the following results:
#
# l = [1]
# append(l, 5)
# print(l)
# [1, 5]
# append(l, "-1")
# print(l)
# [1, 5, '-1']
# append(l)
# print(l)
# []
#
# In[ ]:
# Answer
# ## Exercise 6
# With the code editor, create a module, that contains two functions:
# - fibonacci(n): computes the $n^{th}$ [Fibonacci number](https://en.wikipedia.org/wiki/Fibonacci_number);
# - wallis(n): computes an approximation of $\pi$ using the [Wallis product](https://en.wikipedia.org/wiki/Wallis_product).
#
# Write a script, that uses these two functions.
# In[ ]:
# Answer
# # References
# - [JupyterLab documentation](https://jupyterlab.readthedocs.io/en/latest/index.html).
# - [Official documentation](https://docs.python.org/3/tutorial/index.html).
# - [Scipy lecture notes](http://www.scipy-lectures.org/index.html).
# - [Allen Downey's book](http://www.greenteapress.com/thinkpython/thinkpython.pdf).
#
# ## Exercise 2
# Create the following list with loops:
#
# [['car', 0, 1, 4, 9, 16],
# ['bus', 1, 4, 9, 16, 25],
# ['train', 4, 9, 16, 25, 36]]
#
# In[ ]:
# Answer
# Create a script that prints this list in the following manner:
#
# car 0 1 4 9 16
# bus 1 4 9 16 25
# train 4 9 16 25 36
#
# In[ ]:
# Answer
# ## Exercise 3
# Create a function that returns the sum log of all its parameters (use the `log` function from the `math` module).
#
# In[ ]:
# Answer
# ## Exercise 4
# For the following list of dictionaries, write a script that adds a field `registrations` which is twice the number of accepted papers.
# In[160]:
confs = [{"Name": "NIPS", "Date": 2016, "Location": "Barcelona", "acc_papers": 300},
{"Name": "ICML", "Date": 2016, "Location": "New York City", "acc_papers": 450},
{"Name": "ICML", "Date": 2015, "Location": "Lille", "acc_papers": 250},
{"Name": "AISTATS", "Date": 2016, "Location": "Cadiz", "acc_papers": 100}]
# In[ ]:
# Answer
# ## Exercise 5
# Write a function `append`, that produces the following results:
#
# l = [1]
# append(l, 5)
# print(l)
# [1, 5]
# append(l, "-1")
# print(l)
# [1, 5, '-1']
# append(l)
# print(l)
# []
#
# In[ ]:
# Answer
# ## Exercise 6
# With the code editor, create a module, that contains two functions:
# - fibonacci(n): computes the $n^{th}$ [Fibonacci number](https://en.wikipedia.org/wiki/Fibonacci_number);
# - wallis(n): computes an approximation of $\pi$ using the [Wallis product](https://en.wikipedia.org/wiki/Wallis_product).
#
# Write a script, that uses these two functions.
# In[ ]:
# Answer
# # References
# - [JupyterLab documentation](https://jupyterlab.readthedocs.io/en/latest/index.html).
# - [Official documentation](https://docs.python.org/3/tutorial/index.html).
# - [Scipy lecture notes](http://www.scipy-lectures.org/index.html).
# - [Allen Downey's book](http://www.greenteapress.com/thinkpython/thinkpython.pdf).