#!/usr/bin/env python
# coding: utf-8

# # Chaine d'information d'un système

# ## Analyse fonctionnelle et structurelle
# 
# <img src="https://ericecmorlaix.github.io/img/AnalyseSystemique-GlobaleInformation.svg" alt="Focus sur la chaine d'information">
# 
# Dans un système pluritechnique, la chaine d'information permet :
# - d'**acquérir** des informations en provenance de lui même, d'autres systèmes connectés, et de son utilisateur par l'intermédiaire d'une interface homme/machine (IHM) ;
# - de les **traiter** pour contrôler l'action à réaliser sur la matière d'oeuvre ;
# - et de **communiquer** l'état du système à l'utilisateur ou à d'autres systèmes connectés.
# 
# ### Exemple du Stepper :
# 
# <img src="https://ericecmorlaix.github.io/img/Stepper-Situation.svg" alt="Mise en situation du mini-stepper">
# 
# 
# La chaine d'information du mini-stepper permet :
# - d'**acquérir** l'information du mouvement d'un step au passage de la pédale devant le capteur ILS (Interrupteur à Lame Souple) ;
# - de **traiter** cette information en comptant la durée de l'exercice et le nombre de steps et en calculant le nombre de calories dépensées ;
# - de **communiquer** ces informations à l'utilisateur en les affichant sur l'écran LCD.
# 
# <img src="https://ericecmorlaix.github.io/img/Stepper-Information-Complet.svg" alt="Mise en situation du mini-stepper">
# 
# 
# <!-- Liens drawio :
# - https://www.draw.io/#HericECmorlaix%2FericECmorlaix.github.io%2Fmaster%2Fimg%2FStepper.drawio
# - https://www.draw.io/#Wb!jfwFiHFql0e01yQbhbs1Zm3rpKjqSIpBvLcAukM-Fw-KH97Xee2GTKpgI86tSAPs%2F01DRVMOGWDVRKYO6WJEZAZIOWM2GOOVWAA
# 
# <img src="https://ericecmorlaix.github.io/img/Stepper-Information.svg" alt="Mise en situation du mini-stepper"> -->
# 

# ## La fonction "Acquérir" :
# 
# - L'acquisition de grandeurs physiques se fait par l'intermédiaires de **capteurs**. Un capteur est un composant qui convertit une grandeur physique en un signal exploitable par l'unité de traitement*.
# > Exemples de capteurs de grandeur physique :
#     - sur le stepper : Interrupteur à Lame Souple ILS ;
#     - autres : thermomètre (température), baromètre (pression)...
# 
# - L'acquisition des consignes de l'utilisateur se fait par l'intermédiaire d'une **interface homme/machine** ([IHM](https://www.lebigdata.fr/interface-homme-machine-tout-savoir-sur-les-ihm)) qui intègre des composants capables de convertir des informations humaines en un signal exploitable par l'unité de traitement*.
# > Exemples de composants d'IHM :
#     - sur le stepper : Bouton Poussoir BP ;
#     - autres : Télécommande, potentiomètre...
#     
# * **Un signal exploitable par l'unité de traitement** : très souvent ce signal sera de nature électrique, rendu compatible avec le microcontroleur utilisé pour le traitement de l'information...

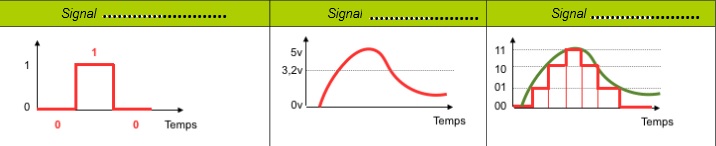
# ## Typologie des signaux logique, analogique et numérique :
# 
# <img src="https://ericecmorlaix.github.io/1SI_2023-2024/CI/logique-analogique-numerique.jpg" alt="Typologie des signaux logique, analogique et numérique">
# 
# ### Ressource vidéo :

# In[19]:


get_ipython().run_cell_magic('HTML', '', '<center>\n<iframe width="560" height="315" src="https://www.youtube-nocookie.com/embed/2PckTQZTdBw?start=16" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>\n</center>\n')


# ## Numération et codage de l’information, changement de base
# 
# ### Problématique :
# 
# Dans notre exemple du stepper, l'information fournie à l'entrée de la chaine par le capteur [ILS](https://fr.wikipedia.org/wiki/Interrupteur_reed) est de type logique (Tout ou Rien [TOR](https://fr.wikipedia.org/wiki/Tout_ou_rien), $0$ ou $1$) or le système de numération adapté pour traiter ce genre d'information est le binaire (à base $2$).
# 
# Par conntre, en sortie, l'information à afficher est destinée à l'utilisateur qui lui compte avec un système de numération décimal (à base $10$).
# 
# Plus généralement, on le reverra en détail plus tard, lorsque la grandeur physique à acquérir sera de type analogique, il nous faudra la numériser pour la traiter avec un microcontrôleur.
# 
# On peut donc d'ores et déjà affirmer que les données qui circuleront dans la chaine d'information seront, à un endroit ou à un autre, numériques (ou pour le moins logique) même si elles représentent autre chose.
# 
# Aussi, pour bien comprendre le codage de l'information qui circulent nous devons être capable de convertir une donnée numérique d'un système de numération à l'autre... 

# ### Les bases :
# 
# #### Système décimal :
# 
# C’est le système de numération que nous utilisons tous les jours. C’est un système de base $10$ car il utilise dix symboles différents :
# $$ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 $$
# 
# C’est un système positionnel car l’endroit où se trouve le symbole dans le nombre définit sa valeur. Le $2$ du nombre décimal $2356$ n’a pas la même valeur celui du nombre décimal $5623$ :
# 
# $2356 	= 2 \times 10^3 + 3 \times 10^2 + 5 \times 10^1 + 6 \times 10^0$ ici le $2$ vaut $2000$
# 
# $5623 	=  5 \times 10^3 + 6 \times 10^2 + 2 \times 10^1 + 3 \times 10^0$  ici le $2$ vaut $20$

# #### Système binaire :
# 
# C’est le système de numération utilisé par les « machines numériques ». C’est un système de base $2$ car il utilise deux symboles différents :
# $$ 0, 1$$
# 
# Pour distinguer le nombre binaire 10110 du nombre décimal 10110 on indique le code ``0b`` (ou le symbole ``%``) avant le nombre ou l’indice $_2$ (ou $_b$) après le nombre.
# 
# $10110_2 = 1 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 16 + 0 + 4 + 2 + 0 = 22_{10}$
# 
# On appel bit (contraction de Binary digIT = BIT) chacun des chiffres d’un nombre binaire.
# 
# Avec un bit on peut distinguer deux états d’une information avec les $2^1 = 2$ nombres soit $1_2$, soit $0_2$.
# 
# Avec $2$ bits on peut distinguer quatre  états d’une information avec les $2^2 = 4$ nombres soit $00_2$, $01_2$, $10_2$, $11_2$.
# 
# Avec $3$ bits  on peut distinguer huit états d’une information avec les $2^3 = 8$ nombres soit $000_2$, $001_2$, $010_2$, $011_2$, $100_2$, $101_2$, $110_2$, $111_2$.
# 
# Avec $8$ bits  on peut distinguer 256 états d’une information avec les $2^8$ nombres allant de $00000000_2 = 0$ à $11111111 = 255$.
# 
# Avec n bits on peut former $2^n$ combinaisons (nombres) différentes.
# 
# Une suite de quatre bits est un quartet , une suite de huit bits est octet.
# 
# Une suite de 16, 32, 64 bits est un mot binaire.

# ### Système hexadécimal.
# 
# C’est un système de base $16$ qui utilise donc seize symboles différents :
# 
# $$ 0,..$$
# 
# Pour distinguer un nombre hexadécimal on indique le code ``0x`` (ou le symbole ``$``) avant le nombre ou l’indice $_{16}$ (ou $_h$) après le nombre.
# 
# Les lettres A à F correspondent respectivement au nombre décimaux ?
# 
# $AC53_{16}$ = ...........?
# 
# <!--
# On utilise le système hexadécimal pour présenter de façon plus condensée un message binaire constitué d'une suite d'octect.
# -->

# ### Correspondance entre nombres de différentes bases :
# 
# <img src="https://ericecmorlaix.github.io/img/Stepper-Correspondance.svg" alt="Tableau de correspondance entre bases">
# 
# <!--
# |   **Décimal**   |   **Binaire**   | **Hexadécimal** |   **Décimal**   |   **Binaire**   | **Hexadécimal** |
# |:---------------:|:---------------:|:---------------:|:---------------:|:---------------:|:---------------:|
# |$0$              |$______$         |$____$           |      $8$        |$______$         |$____$           |
# |$1$              |$______$         |$____$           |      $9$        |$______$         |$____$           |
# |$2$              |$______$         |$____$           |      $10$       |$______$         |$____$           |
# |$3$              |$______$         |$____$           |      $11$       |$______$         |$____$           |
# |$4$              |$______$         |$____$           |      $12$       |$______$         |$____$           |
# |$5$              |$______$         |$____$           |      $13$       |$______$         |$____$           |
# |$6$              |$______$         |$____$           |      $14$       |$______$         |$____$           |
# |$7$              |$______$         |$____$           |      $15$       |$______$         |$____$           |
# -->
# <!--
# <img src="https://ericecmorlaix.github.io/img/Stepper-Correspondance-Complet.svg" alt="Tableau de correspondance entre bases">
# -->

# ### Changement de base :
# 
# #### Conversion d’un nombre décimal en un nombre d’une autre base
# 
# - Une méthode de conversion consiste à décomposer le nombre décimal en une somme de puissances de deux.
# 
# > Par exemple, pour la conversion : $91$ = $01011011_2$
# >
# > On peut écrire :
# >$$91 	= 0 \times 2^7 + 1 \times 2^6 + 0 \times 2^5 + 1 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0$$
# >
# >
# >$$91 = 64 + 16 + 8 + 2 + 1$$
# >
# >En rangeant les puissances de deux dans un tableau, on obtient :
# >
# ><img src="https://ericecmorlaix.github.io/img/Stepper-ConversionBinaire1.svg" alt="Mise en situation du mini-stepper">
# 
# 
# - Une autre méthode de conversion consiste à diviser le nombre décimal à convertir par la base b et conserver le reste de la division. Le quotient obtenu est divisé par b et conserver le reste. Il faut répéter l’opération sur chaque quotient obtenu.
# > Par exemple, pour la conversion : $91$ = $01011011_2$
# >
# ><img src="https://ericecmorlaix.github.io/img/Stepper-ConversionBinaire2.svg" alt="Mise en situation du mini-stepper">
# >
# >Les restes successifs sont écrits, en commençant par le dernier, de la gauche vers la droite. Cette méthode est dite « Méthode des divisions successives ».
# 
# #### Conversion d’un nombre hexadécimal en binaire.
# 
# Chaque symbole du nombre écrit dans le système hexadécimal est remplacé par son équivalent écrit dans le système binaire.
# 
# Exemple : Convertir $ECA_{16}$ = ${1110_2\over E_{16}}{1100_2\over C_{16}}{1010_2\over A_{16}}$ = $1110 1100 1010_2$ 
# 
# 
# #### Conversion d’un nombre binaire en hexadécimal.
# 
# C’est l’inverse de la précédente. Il faut donc regrouper les 1 et les 0 du nombre par 4 en commençant par la droite, puis chaque groupe est remplacé par le symbole hexadécimal correspondant.
# 
# Exemple : Convertir $1100001101111_2$ = ${1_{16}\over 0001_2}{8_{16}\over 1000_2}{6_{16}\over 0110_2}{F_{16}\over 1111_2}$ = $186F_{16}$
# 

# ## Exercices :
# 
# Convertir $9F2_{16}$ en binaire.
# 
# Convertir $001111110101_2$ en hexadécimal.
# 
# Convertir en décimal les nombres binaires suivants : $10110_2$ ; $10001101_2$ ; $1111010111_2$
# 
# Convertir en binaire les nombres décimaux suivants : $37$ ; $189$ ; $205$ ; $2313$.
# 
# Convertir en décimal les nombres hexadécimaux suivants : $92_{16}$ ; $2C0_{16}$ ; $37FD_{16}$.
# 
# Convertir en hexadécimal les nombres décimaux suivants : 75 ; 314 ; 25619.
# 
# Quelle est l’étendue des nombres définis en hexadécimal sur 6 chiffres ?
# 
# Exécuter les opérations $10111101_2 + 101111_2$, $1BF_{16} + A23_{16}$
# 
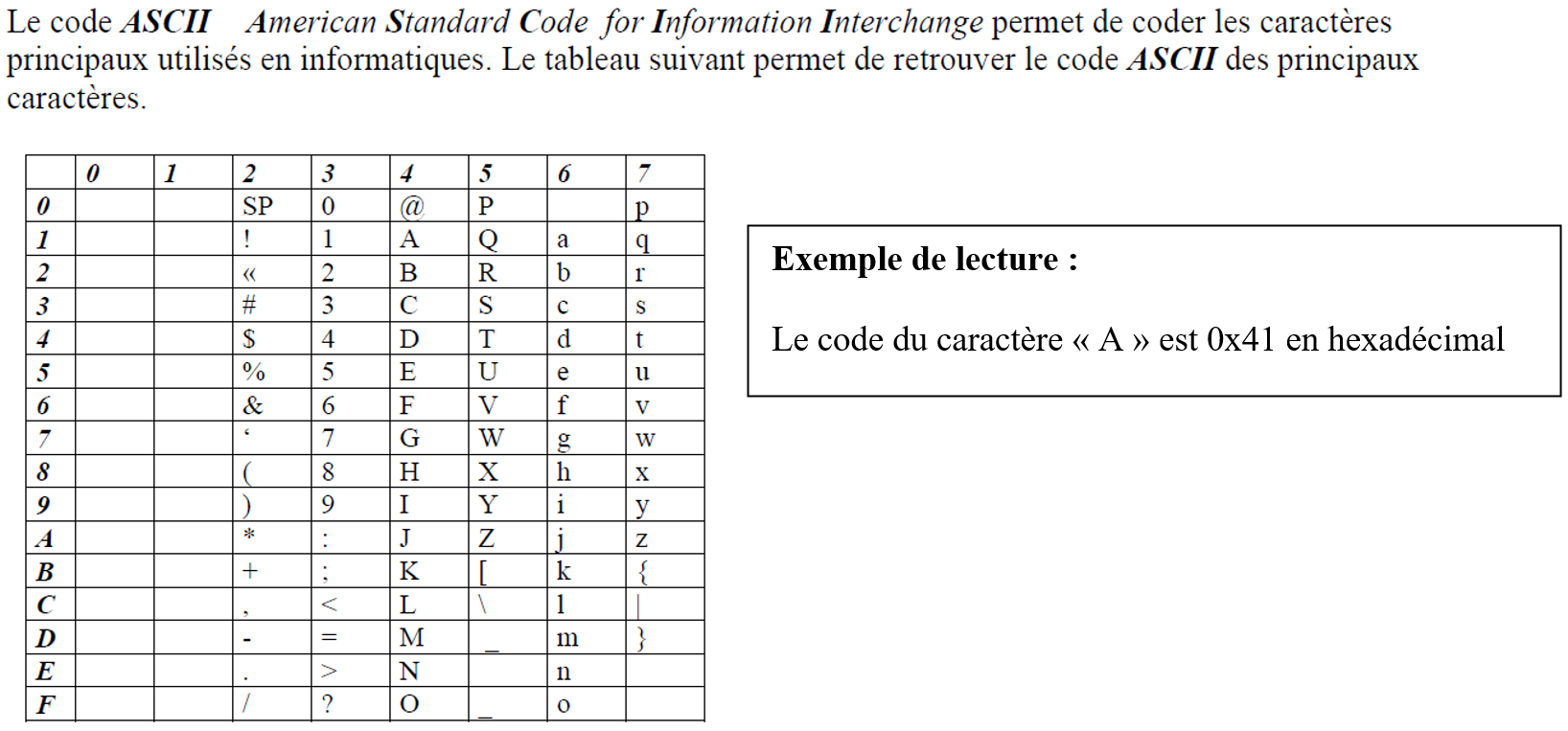
# Quel est le code ASCII en hexadécimal correspondant à la chaine de caractères `1SI` ?
# 
# ><img src="https://ericecmorlaix.github.io/img/1SI_ASCII.png" alt="1SI_ASCII">
# 
# 

# ## Vérification avec Python :
# 
# La fonction `bin()` permet de convertir un nombre en binaire :

# In[ ]:


bin(91)


# In[ ]:


bin(0x5b)


# La fonction `hex()` permet de convertir un nombre en hexadécimal :

# In[ ]:


hex(91)


# In[ ]:


hex(0b1011011)


# La fonction `int()` permet de convertir un nombre en décimal :

# In[ ]:


int(0b1011011)


# In[ ]:


int(0x5b)


# ## Ressources :

# In[1]:


get_ipython().run_cell_magic('HTML', '', '<center>\n    <iframe src="https://player.vimeo.com/video/100900776?byline=0&portrait=0" width="640" height="480" frameborder="0" allow="autoplay; fullscreen" allowfullscreen></iframe>\n<p><a href="https://vimeo.com/100900776">Binary and Decimal Conversion</a> from <a href="https://vimeo.com/user30149681">EICC</a> on <a href="https://vimeo.com">Vimeo</a>.</p>\n</center>\n')


# ## Références au programme :
# 
# <style type="text/css">
# .tg  {border-collapse:collapse;border-spacing:0;}
# .tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;border-color:black;}
# .tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;border-color:black;}
# .tg .tg-cv16{font-weight:bold;background-color:#dae8fc;border-color:inherit;text-align:center}
# .tg .tg-xldj{border-color:inherit;text-align:left}
# </style>
# <table class="tg">
#   <tr>
#     <th class="tg-cv16">Compétences développées</th>
#     <th class="tg-cv16">Connaissances associées</th>    
#   </tr>
#   <tr>
#     <td class="tg-xldj">Caractériser les échanges d’informations</td>
#     <td class="tg-xldj">Natures et caractéristiques des signaux, des
# données, des supports de communication...</td>    
#   </tr>
# </table>

# <a rel="license" href="http://creativecommons.org/licenses/by-sa/4.0/"><img alt="Licence Creative Commons" style="border-width:0" src="https://i.creativecommons.org/l/by-sa/4.0/88x31.png" /></a><br />Ce document est mis à disposition selon les termes de la <a rel="license" href="http://creativecommons.org/licenses/by-sa/4.0/">Licence Creative Commons Attribution -  Partage dans les Mêmes Conditions 4.0 International</a>.
# 
# Pour toute question, suggestion ou commentaire : <a href="mailto:eric.madec@ecmorlaix.fr">eric.madec@ecmorlaix.fr</a>