

 #
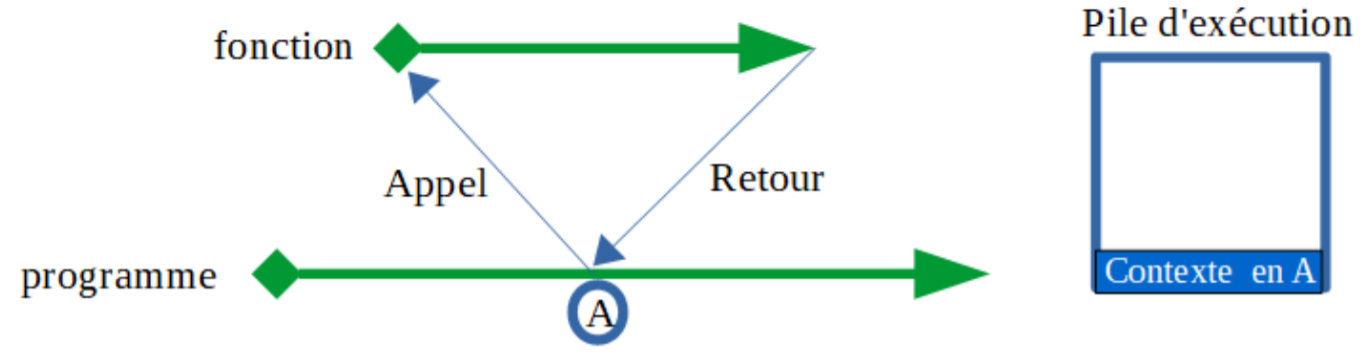
# Au moment où débute cette bifurcation, le processeur sauvegarde un certain nombre d’informations : adresse de retour, état des
# variables, etc.
#
# Toutes ces données forment ce qu’on appelle le contexte du programme, et elles sont stockées dans ce qu’on appelle la pile d’exécution.
#
# À la fin de l’exécution de la fonction, le contexte est sorti pour permettre la poursuite de l’exécution du programme.
#
#
#
# Au moment où débute cette bifurcation, le processeur sauvegarde un certain nombre d’informations : adresse de retour, état des
# variables, etc.
#
# Toutes ces données forment ce qu’on appelle le contexte du programme, et elles sont stockées dans ce qu’on appelle la pile d’exécution.
#
# À la fin de l’exécution de la fonction, le contexte est sorti pour permettre la poursuite de l’exécution du programme.
#
# 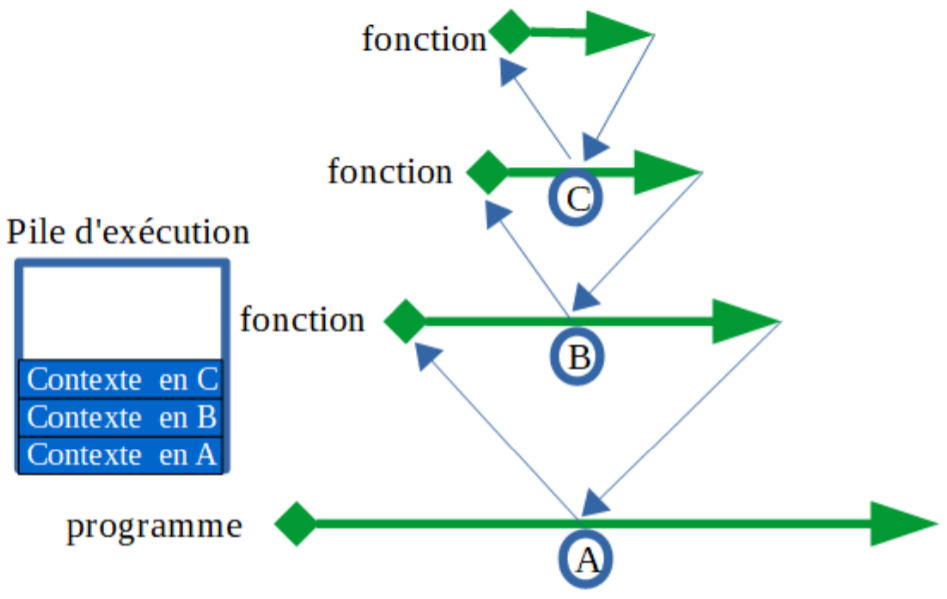 #
# Lors de l’exécution d’une fonction récursive, chaque appel récursif conduit, au moment où il se produit, à un empilement du contexte dans la pile d’exécution.
#
# Lorsqu’au bout de n appels se produit la condition d’arrêt, les différents contextes sont progressivement dépilés pour poursuivre l’exécution de la fonction.
#
# Il est important de prendre conscience qu’**une fonction récursive s’accompagne d’une complexité qui va croître avec le nombre d’appels récursifs** (en général linéairement, mais ce n’est pas une règle, cela dépend du contenu du contexte).
# ## Les trois règles...
#
# A l'instar des robots d’[Azimov](https://fr.wikipedia.org/wiki/Trois_lois_de_la_robotique), les algorithmes récursifs doivent obéir à trois règles :
#
# 1. Un algorithme récursif doit avoir un " état trivial ", cela permet d’avoir une condition d’arrêt.
#
# > Dans notre exemple, il s’agit de : _si la liste est de longueur 1 alors on renvoie le seul élément de la liste_.
#
# 2. Un algorithme récursif doit conduire vers cet " état d’arrêt ", cela permet de ne pas faire une infinité d’appels récursifs.
#
# > Dans notre exemple, à chaque appel récursif, la liste est diminuée d’un élément donc nécessairement elle finira par n’en n’avoir plus qu’un.
#
# 3. Un algorithme récursif s’appelle lui même...
# ## Itératif vs Récursif
#
# Il n’existe pas de réponse définitive à la question de savoir si un algorithme récursif est préférable à un algorithme itératif ou le contraire.
#
# Il a été prouvé que ces deux paradigmes de programmation sont équivalents ; autrement dit, tout algorithme itératif possède une version récursive, et réciproquement.
#
# Le choix du langage peut aussi avoir son importance : un langage fonctionnel est conçu pour exploiter la récursivité et le programmeur est naturellement amené à choisir la version récursive de l’algorithme qu’il souhaite écrire.
#
# À l’inverse, Python, même s’il l’autorise, ne favorise pas l’écriture récursive (limitation basse (1000 par défaut) du nombre
# d’appels récursifs).
#
# Enfin, le choix d’écrire une fonction récursive ou itérative peut dépendre du problème à résoudre : certains problèmes se résolvent particulièrement simplement sous forme récursive.
#
#
# Lors de l’exécution d’une fonction récursive, chaque appel récursif conduit, au moment où il se produit, à un empilement du contexte dans la pile d’exécution.
#
# Lorsqu’au bout de n appels se produit la condition d’arrêt, les différents contextes sont progressivement dépilés pour poursuivre l’exécution de la fonction.
#
# Il est important de prendre conscience qu’**une fonction récursive s’accompagne d’une complexité qui va croître avec le nombre d’appels récursifs** (en général linéairement, mais ce n’est pas une règle, cela dépend du contenu du contexte).
# ## Les trois règles...
#
# A l'instar des robots d’[Azimov](https://fr.wikipedia.org/wiki/Trois_lois_de_la_robotique), les algorithmes récursifs doivent obéir à trois règles :
#
# 1. Un algorithme récursif doit avoir un " état trivial ", cela permet d’avoir une condition d’arrêt.
#
# > Dans notre exemple, il s’agit de : _si la liste est de longueur 1 alors on renvoie le seul élément de la liste_.
#
# 2. Un algorithme récursif doit conduire vers cet " état d’arrêt ", cela permet de ne pas faire une infinité d’appels récursifs.
#
# > Dans notre exemple, à chaque appel récursif, la liste est diminuée d’un élément donc nécessairement elle finira par n’en n’avoir plus qu’un.
#
# 3. Un algorithme récursif s’appelle lui même...
# ## Itératif vs Récursif
#
# Il n’existe pas de réponse définitive à la question de savoir si un algorithme récursif est préférable à un algorithme itératif ou le contraire.
#
# Il a été prouvé que ces deux paradigmes de programmation sont équivalents ; autrement dit, tout algorithme itératif possède une version récursive, et réciproquement.
#
# Le choix du langage peut aussi avoir son importance : un langage fonctionnel est conçu pour exploiter la récursivité et le programmeur est naturellement amené à choisir la version récursive de l’algorithme qu’il souhaite écrire.
#
# À l’inverse, Python, même s’il l’autorise, ne favorise pas l’écriture récursive (limitation basse (1000 par défaut) du nombre
# d’appels récursifs).
#
# Enfin, le choix d’écrire une fonction récursive ou itérative peut dépendre du problème à résoudre : certains problèmes se résolvent particulièrement simplement sous forme récursive.
#  # >
# >Les restes successifs sont écrits, en commençant par le dernier, de la gauche vers la droite. Cette méthode est dite « Méthode des divisions successives ».
#
# Voici un programme itératif qui réalise ce changement de base :
# In[11]:
def decTob(n,b):
assert (b > 1 and b < 17) , "b doit être compris entre 2 et 16"
signes = ["0","1","2","3","4","5","6","7","8","9","A","B","C","D","E","F"]
mot = ""
while n != 0:
mot = signes[n % b] + mot
n = n // b
return mot
# Analysons ce programme :
#
# - La première ligne permet de s’assurer que les conditions sur b sont assurées ;
# - La liste signes nous permet d’avoir accès aux symboles représentant les nombres jusqu’à la base 16 ;
# - On utilisera la variable mot de type str pour le résultat ;
# - Tant que n != 0 (tant que le quotient n’est pas nul), on ajoute par la gauche le reste au résultat et on remplace n par le nouveau quotient n // b.
#
#
# >
# >Les restes successifs sont écrits, en commençant par le dernier, de la gauche vers la droite. Cette méthode est dite « Méthode des divisions successives ».
#
# Voici un programme itératif qui réalise ce changement de base :
# In[11]:
def decTob(n,b):
assert (b > 1 and b < 17) , "b doit être compris entre 2 et 16"
signes = ["0","1","2","3","4","5","6","7","8","9","A","B","C","D","E","F"]
mot = ""
while n != 0:
mot = signes[n % b] + mot
n = n // b
return mot
# Analysons ce programme :
#
# - La première ligne permet de s’assurer que les conditions sur b sont assurées ;
# - La liste signes nous permet d’avoir accès aux symboles représentant les nombres jusqu’à la base 16 ;
# - On utilisera la variable mot de type str pour le résultat ;
# - Tant que n != 0 (tant que le quotient n’est pas nul), on ajoute par la gauche le reste au résultat et on remplace n par le nouveau quotient n // b.
#
# | Contenus | #Capacités attendues | #Commentaires | #
|---|---|---|
| Récursivité. | #Écrire un programme récursif. Analyser le fonctionnement d’un programme récursif. |
# Des exemples relevant de domaines variés sont à privilégier. | #
