#!/usr/bin/env python
# coding: utf-8

# <h1><center><span style="color:#369;background:#fdf;padding: 10px 30px 10px 30px;border: 3px solid #369;border-radius:7px;">Représentation des graphes avec la classe networkx</span></center></h1>

# Commençons par installer le module pour importer la bibliothèque :

# In[ ]:


# Inutile dans CAPYTALE
get_ipython().system('pip install networkx')


# In[ ]:


import networkx as nx #SyntaxWarning à ignorer


# # 1. Les graphes non orientés

# - On crée une instance de la classe Graph de networkx :

# In[ ]:


G = nx.Graph() # crée un graphe vide


# ## Les sommets

# In[ ]:


G.add_node("A")  # ajoute le sommet A

G.add_nodes_from(["B", "C"])  # ajoute plusieurs sommets, ici B et C

H = nx.Graph() # un autre graphe

H.add_nodes_from(G)  # ajoute tous les sommets du graphe G


# - On peut avoir envie de récupérer la liste des sommets :

# In[ ]:


G.nodes() # un objet NodeView pour obtenir tous les sommets


# In[ ]:


list(G.nodes)  # ou list(G.nodes()) pour les avoir sous forme d'une liste


# - Si le sommet existe déjà, l'ajouter ne produit rien :

# In[ ]:


G.add_node("A")
print(G.nodes)  # ou print(G.nodes())


# - On peut même créer rapidement un graphe à n sommets étiquetés par des entiers

# In[ ]:


G1=nx.Graph()
G1.add_nodes_from(range(1,10))
print(G1.nodes)


# - On peut aussi créer rapidement un graphe dont les sommets sont des lettres de l'alphabets

# In[ ]:


G2=nx.Graph()
G2.add_nodes_from("ABCDEF")
print(G2.nodes)


# - Pour récupérer l'ordre du graphe, il y a deux façons :

# In[ ]:


G.number_of_nodes()


# In[ ]:


G.order()


# ## Les arêtes
# 
# - On peut bien sûr ajouter des arêtes en mentionnant les noms des sommets :

# In[ ]:


G.add_edge("A", "B") # ajoute l'arête entre les sommets "A" et "B"
G.add_edges_from([("B", "D"), ("B", "C")])  # ajoute plusieurs arêtes, ici deux


# - On peut même créer les sommets à l'aide des arêtes !

# In[ ]:


G.add_edge("A", "E")  # crée le sommet E et le relie à A


# In[ ]:


list(G.nodes) # on vérifie que le sommet E a bien été créé


# - On peut récupérer la liste des arêtes :

# In[ ]:


G.edges() # un objet EdgeView pour obtenir toutes les arêtes


# In[ ]:


list(G.edges) # ou list(G.edges()) pour les avoir sous forme d'une liste


# - Pour récupérer le nombre d'arêtes, il y a deux façons :

# In[ ]:


G.number_of_edges()


# In[ ]:


G.size()


# - pour tester si deux sommets sont voisins :

# In[ ]:


('A', 'B') in G.edges


# In[ ]:


('B', 'A') in G.edges # comme le graphe n'est pas orienté, ('A','B') est une arête ssi ('B','A') en est une


# <div class="alert alert-warning">Attention à ne pas convertir <code>G.edges</code> en liste car la liste est composée de tuples et le tuple <code>('A','B')</code> est différent de <code>('B','A')</code></div> 

# In[ ]:


L=list(G.edges)


# In[ ]:


('A', 'B') in L


# In[ ]:


('B', 'A') in L # alors que ('B','A') est bien une arête de G


# - Pour supprimer une arête :

# In[ ]:


G.remove_edge('A','E')
G.edges()


# <div class="alert alert-warning">Attention : la métode <code>remove_edge</code> provoque une erreur si on veut supprimer une arête qui n'existait pas</div> 

# In[ ]:


G.remove_edge('A','E') # va provoquer une erreur puisque l'arête n'existe plus


# - Pour supprimer un sommet ainsi que toutes ses arêtes incidentes :

# In[ ]:


G.remove_node('E')
print(G.nodes())
print(G.edges())


# <div class="alert alert-warning">Attention : la métode <code>remove_node</code> provoque une erreur si on veut supprimer une sommet qui n'existe pas</div> 

# In[ ]:


G.remove_node('E') # va provoquer une erreur puisque le sommet n'existe plus


# ## Compléments
# - Pour vérifier si le graphe est orienté ou pas :

# In[ ]:


G.is_directed() # en anglais directed signifie orienté


# - pour obtenir les voisins d'un sommet :

# In[ ]:


list(G.neighbors('B')) # la méthode neighbors() renvoie ce qu'on appelle un itérateur,
# Un itérateur sert à être parcouru à l'aide d'une boucle for mais pour le visualiser
# il faut le convertir en une liste


# - Pour parcourir à l'aide d'une boucle tous les voisins d'un sommet :

# In[ ]:


for s in G.neighbors('B'): # pour parcourir tous les voisins de 'B'
    print(s)


# - Pour obtenir le degré d'un sommet :

# In[ ]:


G.degree('A')


# In[ ]:


G.degree # ou pour les avoir tous


# - Pour obtenir la liste des voisins de chaque sommet :

# In[ ]:


G.adj # les accolades sont vides car le graphe n'est pas pondéré


# # 2. Représenter un graphe non orienté
# 
# - On commence par créer un graphe simple

# In[ ]:


G = nx.Graph()
G.add_edges_from(
    [("A", "B"), ("B", "C"), ("C", "D"), ("D", "A"), ("A", "C"), ("C", "E")]
)


# - Et voici comment le dessiner de manière basique : on doit d'abord importer de la bibliothèque
# `matplotlib`

# In[ ]:


import matplotlib.pyplot as plt
plt.clf() # on efface
nx.draw(G) # on dessine
plt.show() # on montre le dessin


# C'est bien mais il nous manque les noms des sommets !
# 
# Heureusement il est facile de les afficher :

# In[ ]:


plt.clf() # on efface (sinon il y aura 1 seule figure qui contiendra tous les graphes non effacés)
nx.draw(G, with_labels=True)
plt.show()


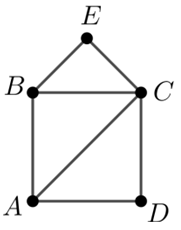
# ### Exercice 1
# Représenter le graphe <code>G1</code> ci-contre (<i>attention, il est possible que vous obteniez un schéma différent, vous devez vérifier qu'il s'agit en fait du même graphe en examinant tous les voisins de chaque sommet</i>) :
# 
# ![graphes_networkx_ex1.png](https://ericecmorlaix.github.io/img/graphes_networkx_ex1.png)

# In[ ]:


# votre code


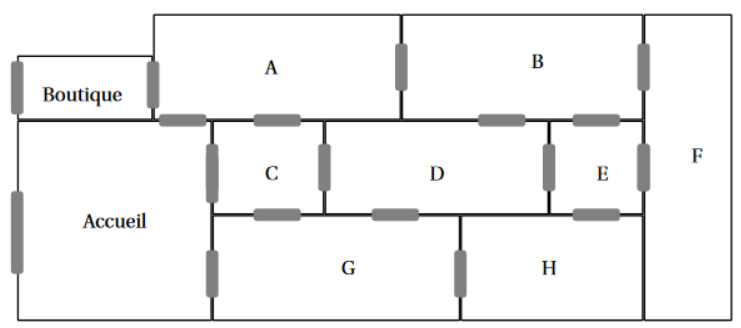
# ### Exercice 2
# Représenter de même le graphe <code>G2</code> associé au plan du musée ci-dessous
# 
# ![graphes_networkx_ex2.png](https://ericecmorlaix.github.io/img/graphes_networkx_ex2.png)

# In[ ]:


# votre code


# ### Exercice 3
# Compléter la fonction <code>matriceDadjacence</code> qui renvoie la matrice d'adjacence d'un graphe simple (orienté ou pas) puis la tester sur les graphes précédents.

# In[ ]:


def matriceDadjacence(G):
    ''' In : un graphe simple G (orienté ou pas)
        Out: la matrice d'adjacence sous forme d'une liste de listes'''
    n= ... # ordre de G càd le nb de sommets
    L=[[0]*n for i in range(n)] # une liste de listes initialisées à 0
    sommets=list(G.nodes) # liste des sommets
    for i in range(n):
        for j in range(n):
            if ... in ...: # si les sommets d'indice i et j sont adjacents
                L[i][j]= ...
    return L


# In[ ]:


# Jeu de tests


# In[ ]:


# Jeu de tests


# In[ ]:


# Test de la fonction précédente
# permet de voir que votre fonction à l'air correcte, c'est le cas si cette cellule ne renvoie pas d'erreur
GTest=nx.Graph()
GTest.add_edges_from([(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 13), (1, 3), (1, 5), (1, 7), (1, 8), (1, 10), (1, 11), (1, 18), (1, 19), (2, 6), (2, 8), (2, 15), (2, 16), (2, 18), (2, 19), (3, 5), (3, 6), (3, 8), (3, 11), (3, 13), (3, 15), (3, 16), (3, 18), (3, 19), (4, 5), (4, 8), (4, 14), (4, 15), (4, 16), (4, 17), (5, 7), (5, 9), (5, 11), (5, 12), (5, 14), (5, 16), (5, 17), (5, 18), (5, 19), (6, 7), (6, 8), (6, 9), (6, 10), (6, 12), (6, 14), (6, 15), (6, 16), (6, 17), (6, 18), (6, 19), (7, 9), (7, 12), (7, 14), (7, 15), (7, 16), (7, 19), (13, 10), (13, 11), (13, 16), (13, 17), (13, 18), (8, 9), (8, 10), (8, 11), (8, 14), (8, 17), (8, 19), (10, 12), (10, 15), (10, 16), (10, 17), (10, 18), (11, 9), (11, 15), (11, 16), (11, 17), (11, 18), (18, 12), (18, 14), (18, 15), (18, 17), (19, 9), (19, 16), (19, 17), (15, 9), (15, 16), (16, 12), (14, 12), (17, 12), (9, 12)])
assert matriceDadjacence(GTest)==[[0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0], [1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0], [1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0], [1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1], [1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0], [0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0], [0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1], [0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0], [0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1], [0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0], [0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1], [0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0]]


# ### Exercice 4
# Compléter la fonction <code>listeDadjacence</code> qui renvoie la liste d'adjacence d'un graphe G sous forme de dictionnaire, puis la tester sur les graphes précédents.

# In[ ]:


def listeDadjacence(G):
    ''' In : un graphe simple G (orienté ou pas)
        Out: la liste d'adjacence de G sous forme d'un dictionnaire'''
    d=dict() # ou d={} pour créer un dictionnaire vide
    for s in G.nodes(): # pour chaque sommet s, on initialise la liste des voisins à une liste vide
        d[s]= ... # correspondra à la liste des successeurs de s
    for s in G.nodes():# pour chaque sommet s
        for v in G.nodes():# pour chaque sommet v
            if ... in ...:# si v est le successeur de s
                ... # on ajoute le sommet v à la liste des successeurs de s
    return d


# In[ ]:


# Jeu de tests


# In[ ]:


# Jeu de tests


# In[ ]:


# Test de la fonction précédente
# permet de voir que votre fonction à l'air correcte, c'est le cas si cette cellule ne renvoie pas d'erreur
GTest=nx.Graph()
GTest.add_edges_from([(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 13), (1, 3), (1, 5), (1, 7), (1, 8), (1, 10), (1, 11), (1, 18), (1, 19), (2, 6), (2, 8), (2, 15), (2, 16), (2, 18), (2, 19), (3, 5), (3, 6), (3, 8), (3, 11), (3, 13), (3, 15), (3, 16), (3, 18), (3, 19), (4, 5), (4, 8), (4, 14), (4, 15), (4, 16), (4, 17), (5, 7), (5, 9), (5, 11), (5, 12), (5, 14), (5, 16), (5, 17), (5, 18), (5, 19), (6, 7), (6, 8), (6, 9), (6, 10), (6, 12), (6, 14), (6, 15), (6, 16), (6, 17), (6, 18), (6, 19), (7, 9), (7, 12), (7, 14), (7, 15), (7, 16), (7, 19), (13, 10), (13, 11), (13, 16), (13, 17), (13, 18), (8, 9), (8, 10), (8, 11), (8, 14), (8, 17), (8, 19), (10, 12), (10, 15), (10, 16), (10, 17), (10, 18), (11, 9), (11, 15), (11, 16), (11, 17), (11, 18), (18, 12), (18, 14), (18, 15), (18, 17), (19, 9), (19, 16), (19, 17), (15, 9), (15, 16), (16, 12), (14, 12), (17, 12), (9, 12)])
assert listeDadjacence(GTest)=={0: [1, 2, 3, 4, 5, 6, 7, 13], 1: [0, 3, 5, 7, 8, 10, 11, 18, 19], 2: [0, 6, 8, 18, 19, 15, 16], 3: [0, 1, 5, 6, 13, 8, 11, 18, 19, 15, 16], 4: [0, 5, 8, 15, 16, 14, 17], 5: [0, 1, 3, 4, 7, 11, 18, 19, 16, 14, 17, 9, 12], 6: [0, 2, 3, 7, 8, 10, 18, 19, 15, 16, 14, 17, 9, 12], 7: [0, 1, 5, 6, 19, 15, 16, 14, 9, 12], 13: [0, 3, 10, 11, 18, 16, 17], 8: [1, 2, 3, 4, 6, 10, 11, 19, 14, 17, 9], 10: [1, 6, 13, 8, 18, 15, 16, 17, 12], 11: [1, 3, 5, 13, 8, 18, 15, 16, 17, 9], 18: [1, 2, 3, 5, 6, 13, 10, 11, 15, 14, 17, 12], 19: [1, 2, 3, 5, 6, 7, 8, 16, 17, 9], 15: [2, 3, 4, 6, 7, 10, 11, 18, 16, 9], 16: [2, 3, 4, 5, 6, 7, 13, 10, 11, 19, 15, 12], 14: [4, 5, 6, 7, 8, 18, 12], 17: [4, 5, 6, 13, 8, 10, 11, 18, 19, 12], 9: [5, 6, 7, 8, 11, 19, 15, 12], 12: [5, 6, 7, 10, 18, 16, 14, 17, 9]}


# ### Exercice 5
# Compléter la fonction <code>matriceEnDictionnaire</code> puis la tester sur un jeu de tests (qui pourra faire appel aux graphes précédents et aux fonctions précédentes).

# In[ ]:


def matriceEnDictionnaire(L,sommets):
    ''' In : une matrice d'adjacence L sous forme d'une liste de listes et une liste de sommets
        Out: la liste d'adjacence sous forme d'un dictionnaire'''
    n=len(L) # ou n=len(sommets) le nombre sommets
    d=dict() # ou d={}
    for i in range(n): # pour chaque sommet s, on initialise la liste des voisins à une liste vide
        d[...]= ... # on initialise le sommet d'indice i (il faut se servir de la liste sommets)
    for i in range(n):# pour chaque sommet s
        for j in range(n):# pour chaque sommet v
            if  ...:# si i et j sont voisins
                ... # on ajoute le sommet d'indice j à la liste des successeurs du sommet d'indice i
    return d


# In[ ]:


# Jeu de tests


# In[ ]:





# In[ ]:


# Jeu de tests



# In[ ]:





# In[ ]:


# Test de la fonction précédente
# permet de voir que votre fonction à l'air correcte, c'est le cas si cette cellule ne renvoie pas d'erreur
GTest=nx.Graph()
GTest.add_edges_from([(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 13), (1, 3), (1, 5), (1, 7), (1, 8), (1, 10), (1, 11), (1, 18), (1, 19), (2, 6), (2, 8), (2, 15), (2, 16), (2, 18), (2, 19), (3, 5), (3, 6), (3, 8), (3, 11), (3, 13), (3, 15), (3, 16), (3, 18), (3, 19), (4, 5), (4, 8), (4, 14), (4, 15), (4, 16), (4, 17), (5, 7), (5, 9), (5, 11), (5, 12), (5, 14), (5, 16), (5, 17), (5, 18), (5, 19), (6, 7), (6, 8), (6, 9), (6, 10), (6, 12), (6, 14), (6, 15), (6, 16), (6, 17), (6, 18), (6, 19), (7, 9), (7, 12), (7, 14), (7, 15), (7, 16), (7, 19), (13, 10), (13, 11), (13, 16), (13, 17), (13, 18), (8, 9), (8, 10), (8, 11), (8, 14), (8, 17), (8, 19), (10, 12), (10, 15), (10, 16), (10, 17), (10, 18), (11, 9), (11, 15), (11, 16), (11, 17), (11, 18), (18, 12), (18, 14), (18, 15), (18, 17), (19, 9), (19, 16), (19, 17), (15, 9), (15, 16), (16, 12), (14, 12), (17, 12), (9, 12)])
L=[[0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0], [1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0], [1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0], [1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1], [1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0], [0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0], [0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1], [0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0], [0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1], [0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0], [0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1], [0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0]]
sommets=list(GTest.nodes)
assert matriceEnDictionnaire(L,sommets)=={0: [1, 2, 3, 4, 5, 6, 7, 13], 1: [0, 3, 5, 7, 8, 10, 11, 18, 19], 2: [0, 6, 8, 18, 19, 15, 16], 3: [0, 1, 5, 6, 13, 8, 11, 18, 19, 15, 16], 4: [0, 5, 8, 15, 16, 14, 17], 5: [0, 1, 3, 4, 7, 11, 18, 19, 16, 14, 17, 9, 12], 6: [0, 2, 3, 7, 8, 10, 18, 19, 15, 16, 14, 17, 9, 12], 7: [0, 1, 5, 6, 19, 15, 16, 14, 9, 12], 13: [0, 3, 10, 11, 18, 16, 17], 8: [1, 2, 3, 4, 6, 10, 11, 19, 14, 17, 9], 10: [1, 6, 13, 8, 18, 15, 16, 17, 12], 11: [1, 3, 5, 13, 8, 18, 15, 16, 17, 9], 18: [1, 2, 3, 5, 6, 13, 10, 11, 15, 14, 17, 12], 19: [1, 2, 3, 5, 6, 7, 8, 16, 17, 9], 15: [2, 3, 4, 6, 7, 10, 11, 18, 16, 9], 16: [2, 3, 4, 5, 6, 7, 13, 10, 11, 19, 15, 12], 14: [4, 5, 6, 7, 8, 18, 12], 17: [4, 5, 6, 13, 8, 10, 11, 18, 19, 12], 9: [5, 6, 7, 8, 11, 19, 15, 12], 12: [5, 6, 7, 10, 18, 16, 14, 17, 9]}


# ### Exercice 6
# Compléter la fonction <code>dictionnaireEnMatrice</code> qui fait l'inverse de la fonction précédente puis la tester à l'aide des graphes précédents et des fonctions précédentes.

# In[ ]:


def dictionnaireEnMatrice(d):
    ''' In : un dictionnaire où les clés sont les sommets et les valeurs les listes des voisins
        Out: la matrice d'adjacence associée'''
    n=len(d) # nb de sommets
    sommets=list(d.keys()) # la liste des sommets
    L=[[0]*n for i in range(n)] # une liste de listes initialisées à 0
    for i in range(n):# pour chaque sommet s
        for j in range(n):# pour chaque sommet v
            if ... in ...:# si le sommet d'indice i est le successeur de celui d'indice j
                L[i][j]= ...
    return L,sommets


# In[ ]:


# Jeu de tests


# In[ ]:





# In[ ]:





# In[ ]:





# In[ ]:


# Jeu de tests


# In[ ]:





# In[ ]:





# In[ ]:





# In[ ]:


# Test de la fonction précédente
# permet de voir que votre fonction à l'air correcte, c'est le cas si cette cellule ne renvoie pas d'erreur
GTest=nx.Graph()
GTest.add_edges_from([(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 13), (1, 3), (1, 5), (1, 7), (1, 8), (1, 10), (1, 11), (1, 18), (1, 19), (2, 6), (2, 8), (2, 15), (2, 16), (2, 18), (2, 19), (3, 5), (3, 6), (3, 8), (3, 11), (3, 13), (3, 15), (3, 16), (3, 18), (3, 19), (4, 5), (4, 8), (4, 14), (4, 15), (4, 16), (4, 17), (5, 7), (5, 9), (5, 11), (5, 12), (5, 14), (5, 16), (5, 17), (5, 18), (5, 19), (6, 7), (6, 8), (6, 9), (6, 10), (6, 12), (6, 14), (6, 15), (6, 16), (6, 17), (6, 18), (6, 19), (7, 9), (7, 12), (7, 14), (7, 15), (7, 16), (7, 19), (13, 10), (13, 11), (13, 16), (13, 17), (13, 18), (8, 9), (8, 10), (8, 11), (8, 14), (8, 17), (8, 19), (10, 12), (10, 15), (10, 16), (10, 17), (10, 18), (11, 9), (11, 15), (11, 16), (11, 17), (11, 18), (18, 12), (18, 14), (18, 15), (18, 17), (19, 9), (19, 16), (19, 17), (15, 9), (15, 16), (16, 12), (14, 12), (17, 12), (9, 12)])
L=[[0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0], [1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0], [1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0], [1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1], [1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1], [1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0], [0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0], [0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1], [0, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0], [0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1], [0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0], [0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0], [0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1], [0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0]]
sommets=list(GTest.nodes)
d={0: [1, 2, 3, 4, 5, 6, 7, 13], 1: [0, 3, 5, 7, 8, 10, 11, 18, 19], 2: [0, 6, 8, 18, 19, 15, 16], 3: [0, 1, 5, 6, 13, 8, 11, 18, 19, 15, 16], 4: [0, 5, 8, 15, 16, 14, 17], 5: [0, 1, 3, 4, 7, 11, 18, 19, 16, 14, 17, 9, 12], 6: [0, 2, 3, 7, 8, 10, 18, 19, 15, 16, 14, 17, 9, 12], 7: [0, 1, 5, 6, 19, 15, 16, 14, 9, 12], 13: [0, 3, 10, 11, 18, 16, 17], 8: [1, 2, 3, 4, 6, 10, 11, 19, 14, 17, 9], 10: [1, 6, 13, 8, 18, 15, 16, 17, 12], 11: [1, 3, 5, 13, 8, 18, 15, 16, 17, 9], 18: [1, 2, 3, 5, 6, 13, 10, 11, 15, 14, 17, 12], 19: [1, 2, 3, 5, 6, 7, 8, 16, 17, 9], 15: [2, 3, 4, 6, 7, 10, 11, 18, 16, 9], 16: [2, 3, 4, 5, 6, 7, 13, 10, 11, 19, 15, 12], 14: [4, 5, 6, 7, 8, 18, 12], 17: [4, 5, 6, 13, 8, 10, 11, 18, 19, 12], 9: [5, 6, 7, 8, 11, 19, 15, 12], 12: [5, 6, 7, 10, 18, 16, 14, 17, 9]}
assert dictionnaireEnMatrice(d)==(L,sommets)


# # 3. Les graphes orientés

# - On crée une instance de la classe DiGraph de networkx :

# In[ ]:


DG = nx.DiGraph() # crée un graphe orienté vide


# - Ensuite, ça fonctionne exactement comme pour les graphes non orienté

# In[ ]:


DG.add_node(0)  # ajoute le sommet 0
DG.add_nodes_from([1,2])  # ajoute plusieurs sommets, ici 1 et 2


# In[ ]:


DG.nodes()


# In[ ]:


DG.add_edge(1,2) # ajoute l'arc reliant 1 à 2
DG.add_edges_from([(0,1), (1,0)])  # ajoute plusieurs arcs, ici deux


# In[ ]:


DG.edges() # un objet OutEdgeView pour obtenir toutes les arcs


# - On peut vérifier que l'arc (1,2) existe mais pas l'arc (2,1)

# In[ ]:


(1,2) in DG.edges()


# In[ ]:


(2,1) in DG.edges()


# - BIen sûr ici, notre graphe <code>DG</code> est orienté :

# In[ ]:


DG.is_directed()


# In[ ]:


DG.degree() # on a aussi les degrés qui sont ici la somme des degrés entrant et des degrés sortant


# # 4. Représenter un graphe orienté
# 
# - Cela fonctionne comme pour les graphes orientés

# In[ ]:


DG = nx.DiGraph()
DG.add_edges_from([(0,1),(1,2),(2,3),(3,0),(0,2),(2,0)])
import matplotlib.pyplot as plt
plt.clf() # on efface
nx.draw(DG, with_labels=True) # on dessine
plt.show() # on montre le dessin


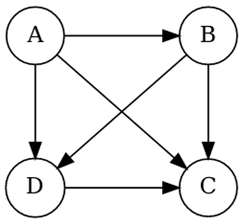
# ### Exercice 7
# Représenter le graphe orienté ci-dessous.
# ![graphes_networkx_ex7.png](https://ericecmorlaix.github.io/img/graphes_networkx_ex7.png)

# In[ ]:


# votre code


# ### Exercice 8
# A l'aide des fonctions précédentes, donner sa matrice d'adjacence et la liste des prédécesseurs. Vérifiez que ce sont les bons résultats.

# In[ ]:


# votre code


# In[ ]:


# votre code


# ### Exercice 9
# Compléter la fonction <code>degreSortant</code> ci-dessous qui renvoie le degré sortant d'un sommet d'un graphe orienté G, puis la tester.

# In[ ]:


def degreSortant(G,s):
    ''' In : un graphe G orienté et un sommet s
        Out: le degré sortant de s'''
    cpt=0
    for t in G.nodes():# pour chaque joueur t
        if ... in ...:# s'il y a un arc de s vers t, càd si s a gagné contre t
            ...
    return cpt


# In[ ]:


# Jeu de tests


# In[ ]:


# Test de la fonction précédente
# permet de voir que votre fonction à l'air correcte, c'est le cas si cette cellule ne renvoie pas d'erreur
DGAlea = nx.DiGraph()
DGAlea.add_edges_from([(1, 0), (1, 2), (1, 4), (1, 5), (1, 6), (1, 8), (1, 9), (0, 5), (0, 6), (0, 7), (0, 8), (2, 0), (2, 3), (2, 4), (2, 8), (2, 9), (3, 0), (3, 1), (3, 4), (3, 5), (3, 7), (3, 9), (4, 0), (4, 5), (4, 7), (4, 8), (4, 9), (5, 2), (5, 8), (6, 2), (6, 3), (6, 4), (6, 5), (6, 7), (6, 9), (7, 1), (7, 2), (7, 5), (7, 8), (8, 3), (8, 6), (8, 9), (9, 0), (9, 5), (9, 7)])
assert [degreSortant(DGAlea,s) for s in DGAlea.nodes()]==[7, 4, 5, 5, 2, 6, 3, 3, 4, 6]