#
# L'objectif de cette étude est de calculer les efforts sur la béquille en phase de "béquillage".
# ## Hypothèses :
#
# - La répartition des charges et la géométrie du système permet d'effectuer une étude plane dans le plan $(G, \overrightarrow{x}, \overrightarrow{y})$.
#
# - L'étude s'effectue durant la phase de béquillage.
#
# - On suppose une action nulle en $B$ entre la roue arrière et le sol.
#
# - Le contact du sol avec la roue avant est modélisé dans le plan, par une liaison ponctuelle de normale $(A, \overrightarrow{y})$ supposée parfaite (sans frottement).
#
# - Le contact de la béquille avec le sol est modélisé dans le plan, par une liaison ponctuelle de normale $(D, \overrightarrow{y})$.
#
# - Le point $G$ représente le centre de gravité du système étudié (moto, pilote et bagages).
#
# ## Données :
#
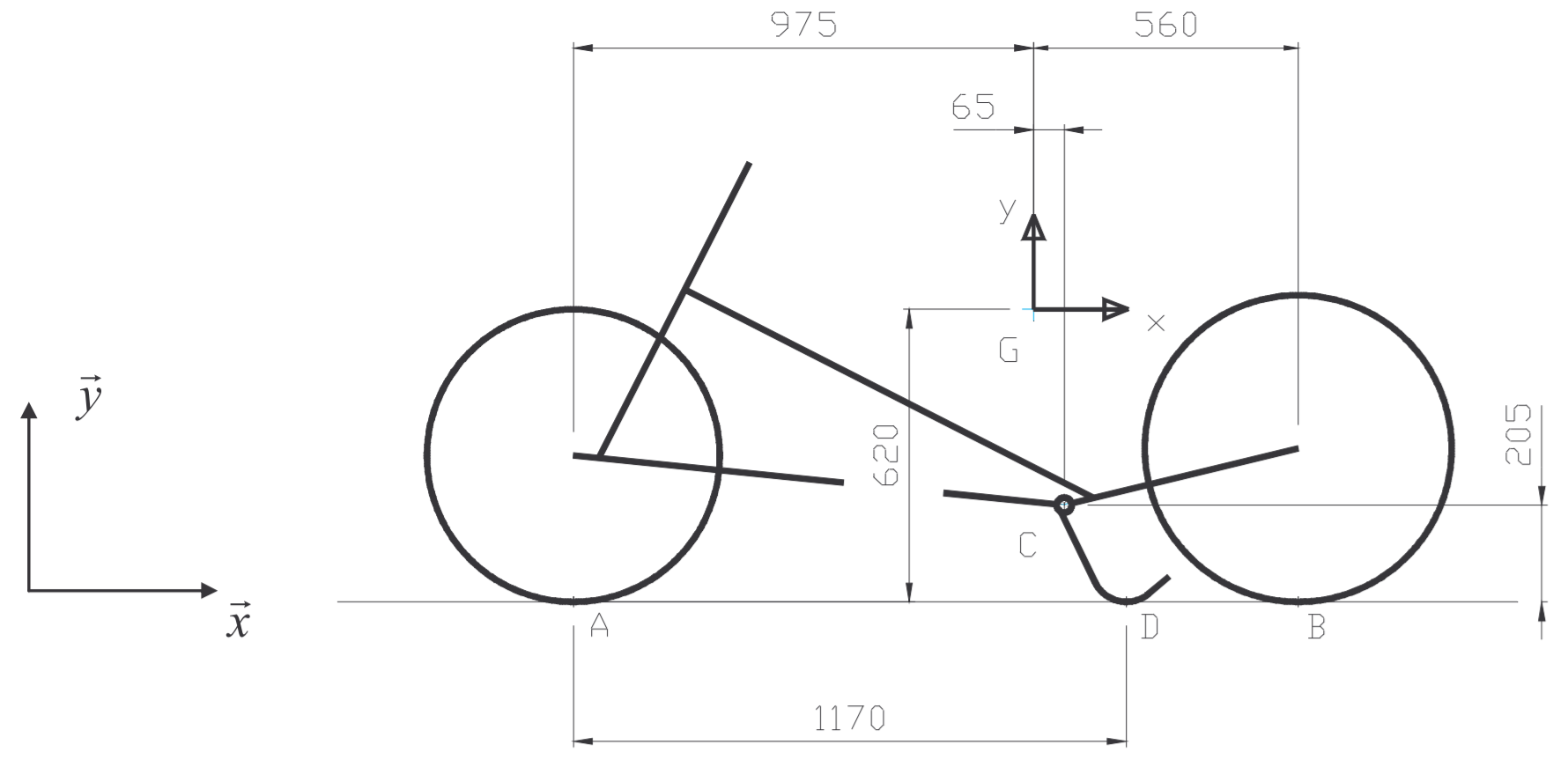
# - Les dimensions sont fournies sur la figure ci-dessous.
#
# - La masse totale à prendre en compte est $m = 370 kg$.
#
#
# 
# ## Bilan des actions mécaniques sur le système S = { moto + pilote + bagage} :
# - Modéliser l'action en B du sol sur la roue arrière compte tenu des hypothèses :
#
# $\overrightarrow{B_{sol \to S}} = $
# - Modéliser l'action de la pesanteur sur le système étudié :
#
# $\overrightarrow{P_{pesanteur \to S}} = $
# - Dresser le tableau modélisant les actions mécaniques transmissibles dans une liaison ponctuelle de normale $\overrightarrow{y}$ :
#
# | F | M |
# |:---:|:---:|
# | ... | ... |
# | ... | ... |
# | ... | ... |
# - En déduire le modèle de l'action de contact en A du sol sur la roue avant :
#
# $\overrightarrow{A_{sol \to S}} = $
#
# - En déduire le modèle de l'action de contact en D du sol sur la béquille :
#
# $\overrightarrow{D_{sol \to S}} = $
# ## Etude de l'équilibre statique du système S = { moto + pilote + bagage} :
# - Exprimer le moment en A de l'action en B du sol sur la roue arrière :
#
# $\overrightarrow{M_A(\overrightarrow{B_{sol \to S}})} = $
# - Exprimer le moment en A de l'action de la pesanteur sur le système étudié :
#
# $\overrightarrow{M_A(\overrightarrow{P_{pesanteur \to S}})} = $
# - Exprimer le moment en A de l'action en A du sol sur la roue avant :
#
# $\overrightarrow{M_A(\overrightarrow{A_{sol \to S}})} = $
# - Exprimer le moment en A de l'action de contact en D du sol sur la béquille :
#
# $\overrightarrow{M_A(\overrightarrow{D_{sol \to S}})} = $
# Pour que le système S = { moto + pilote + bagage} soit en équilibre statique il faut d'une part que $\sum\overrightarrow{M_A(\overrightarrow{F_{ext \to S}})} = \overrightarrow{0}$
#
# - En déduire l'intensité de l'action de contact en D du sol sur la béquille :
#
# ...
#
# ...
#
# $\|\overrightarrow{D_{sol \to S}}\| = $
# De plus, pour que le système S = { moto + pilote + bagage} soit en équilibre statique il faut d'autre part que $\sum\overrightarrow{F_{ext \to S}} = \overrightarrow{0}$
#
# - En déduire l'intensité de l'action de contact en A du sol sur la roue avant :
#
# ...
#
# ...
#
# $\|\overrightarrow{A_{sol \to S}}\| = $
# ## Références au programme :
#
# #### MODÉLISER ET RÉSOUDRE
#
#
# | Compétences développées | #Connaissances associées | #
|---|---|
| Modéliser les actions mécaniques | #Torseurs d’actions mécaniques transmissibles, de contact ou à distance Réciprocité mouvement relatif/actions mécaniques associées |
#
| Déterminer les actions mécaniques (inconnues statiques de liaisons ou action mécanique extérieure) menant à l’équilibre statique d’un mécanisme, d’un ouvrage ou d’une structure | #Principe fondamental de la statique | #