Logique de la chaine d'information :¶

Mise en situation :¶

Nous allons découvrir la logique fondamentale qui permet de traiter l'information d'un système dont nous décrirons le comportement en utilisant différents moyens.

Focus sur la fonction traiter de la chaine d'information

Pour illustrer notre propos, nous étudierons, dans un premier temps, le cas d'un simple système par Va et Vient* qui permet de commander l’éclairage d’une pièce depuis deux endroits différents ?*

cf document pdf associé : Description de la Logique d'un Va Et Vient

In [1]:

from IPython.display import HTML
HTML('''<figure>
<iframe width="600" height="340" src="https://www.brun-videographie.com/iframe/VA-ET-VIENT/VA-ET-VIENT.html"></iframe>
</figure>''')

Out[1]:

Définition :¶

Une fonction logique est une relation établie entre une variable logique de sortie et une ou plusieurs variables logiques d’entrée.

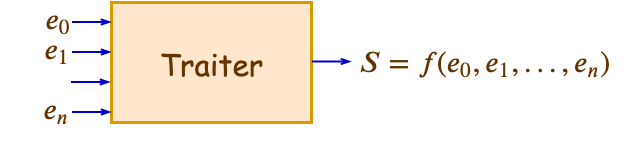
Ces variables d’entrée et de sortie sont dites logiques car elles ne peuvent prendre que deux valeurs (niveaux ou états) distinctes et non simultanées :

soit Vraies = $1$ ;
soit Fausses = $0$.

Ce sont des variables binaires, de type booléennes.

Car pour étudier ces fonctions de variables binaires, on utilise l’algèbre de George BOOLE (mathématicien britannique du XIX siècle), qui a permis le développement des automatismes et de l’informatique...

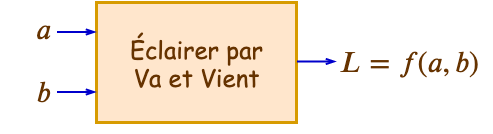
Dans notre exemple de système d’éclairage par va et vient* :*

L’état allumé ou éteint d’une lampe (L) d’éclairage d’une pièce dépend de l’état d’un interrupteur (a) situé à un des accès de la pièce et de celui d’un interrupteur (b) situé à l’autre accès de la pièce.

A faire vous-même - Compléter les entrées et sortie de la fonction traiter du va et vient :

Description d'une fonction logique¶

Proposition logique littérale :¶

Une fonction logique peut se décrire par une phrase établissant une relation de cause à effet (si...alors) entre les entrées et la sortie.

Pour notre exemple de système d’éclairage par va et vient* :*

SI l’interrupteur a est NON actionné ET l’interrupteur b est actionné OU SI l’interrupteur a est actionné ET l’interrupteur b est NON actionné ALORS la lampe L est allumée.

Equation logique (Equation booléenne) :¶

Pour alléger l’écriture et rendre possible l’application de l’algèbre de Boole, on code la proposition logique sous la forme d’une équation.

Le ET se traduit par $\bullet$, le OU se traduit par $+$, le ALORS se traduit par $=$, le NON se traduit par une barre sur la $\overline{variable}$.

Pour notre exemple de système d’éclairage par va et vient* :*

A faire vous-même - Ecrire l'équation booléenne du va et vient :

$L =\overline{a}\bullet b + a\bullet\overline{b}$

Complément : les propriétés de l’algèbre de Boole ¶

Table de vérité :¶

Pour décrire le résultat d’une fonction logique en fonction de l’état de ses entrées on dresse un tableau ordonné appelé table de vérité.

Elle permet de faire l’inventaire de toutes les combinaisons possibles. Le nombre de combinaisons est $2^n$ avec $n$ le nombre d’entrées

Pour notre exemple de système d’éclairage par va et vient* :*

A faire vous-même - Compléter la table de vérité du va et vient :

Tableau d'inventaire des principales fonctions logiques :¶

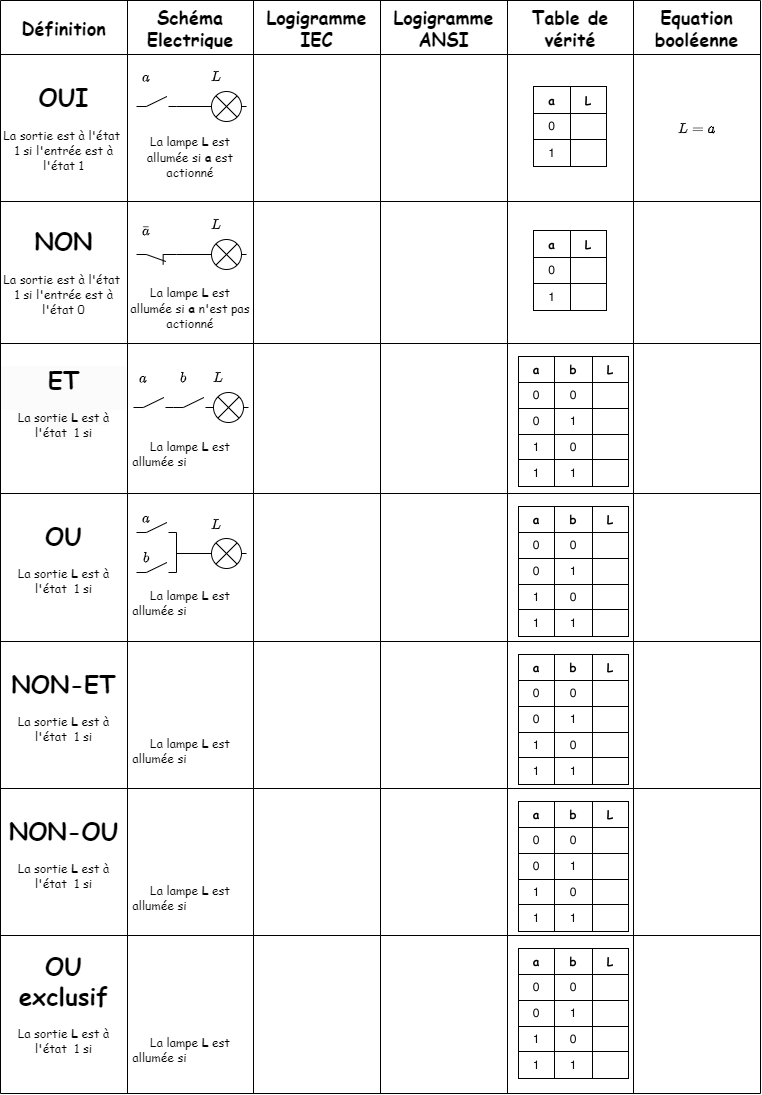
A faire vous-même :

Compléter le tableau ci-dessus à partir d'une recherche web et en expérimentant par simulation le fonctionnement de chaque porte logique de base sur https://logic.ly/demo

cf document pdf associé : Tableau des Fonctions Logiques

Exemple de ressource du web :¶

In [1]:

from IPython.display import HTML
HTML('''<iframe src="https://player.vimeo.com/video/101087321?byline=0&portrait=0" width="640" height="480" frameborder="0" allow="autoplay; fullscreen" allowfullscreen></iframe>
<p><a href="https://vimeo.com/101087321">Logic Gates, Symbols, and Boolean Expressions</a> from <a href="https://vimeo.com/user30149681">EICC</a> on <a href="https://vimeo.com">Vimeo</a>.</p>
</center>''')

Out[1]:

Logic Gates, Symbols, and Boolean Expressions from EICC on Vimeo.

Prolongement :

Simuler puis Expérimenter le fonctionnement de chaque porte logique de base avec une carte BBC micro:bit

On utilisera les boutons-poussoir A et B pour faire les entrées et on affichera en sortie sur la matrice à LEDs un pour vrai et un pour faux.

Lois de De Morgan :¶
Les deux égalités du théorème de DE MORGAN permettent de simplifier les expressions logiques comportant des sommes ou produits complémentés.
$$\overline{a \bullet b} = \overline{a} + \overline{b}$$
$$\overline{a + b} = \overline{a} \bullet \overline{b}$$

Et elles permettent la modification d'une expression afin de réaliser la fonction logique correspondante à partir d'opérateurs logiques NAND et/ou NOR.

Pour cela on complémente deux fois l’expression et on casse la barre du bas en changeant d’opérateur. On réitère cette opération autant de fois que nécessaire.

...

Exercice d'application - Google doodle

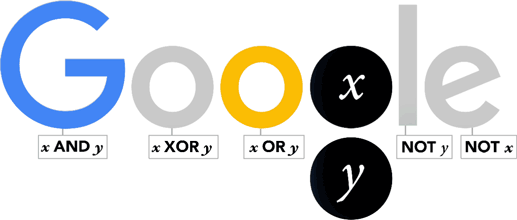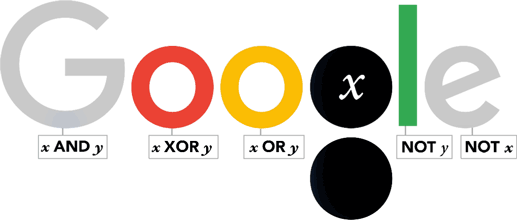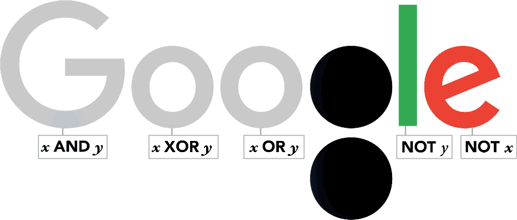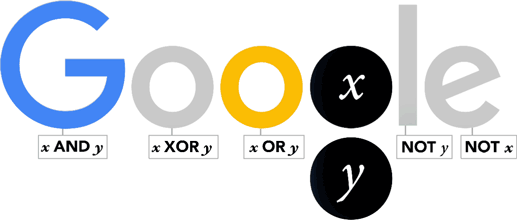
Répondre aux questions du notebook

Proposition de correction¶

A qui Google rendait hommage le 2 novembre 2015 en mettant sur la page d'accueil de son moteur de recherche le doodle ci-dessus ?

George BOOLE ;

Quelles étaient les raisons de cet hommage rendu par Google ?

200ième anniversaire de la naissance de George BOOLE ;

Qu'est-ce qu'une variable booléenne ?

une variable binaire, qui ne peut prendre que deux valeur soit 0 soit 1 ;

Qu'elles sont les principales fonctions (opérations) booléennes ?

les fonctions logique NON (not), ET (and) et OU (or) ;

Expliquer en observant le gif animé du doodle ci-dessus, les conditions pour que :

le G s'allume en bleu :

x ET y à 1 ;

le deuxième o s'allume en jaune :

x OU y à 1 ;

le l s'allume en vert :

NON y à 1 ;

le e s'allume en rouge :

NON x à 1 ;

le premier o s'allume en rouge :

x OU y à 1 mais pas les deux à la fois, c'est un OU exclusif ;

Description d'une fonction logique (Suite) :¶

Schéma à contacts :¶

Il s’agit de représenter la fonction logique sous la forme d’un schéma à contact de technologie électrique.

Un contact ouvert au repos (NO) représente une variable d’entrée dont l’état vrai (=1) est requis, un contact fermé au repos (NF) représente une variable d’entrée dont l’état faux (=0) est requis, et une charge (bobine ou lampe) représente la variable de sortie, la fonction ET est traduite en disposant les contacts en série, la fonction OU est traduite en disposant les contacts en parallèle.

Pour notre exemple de système d’éclairage par va et vient* :*

A faire vous-même - Tracer un schéma à contacts pour le va et vient :

Logigramme :¶

Une fonction logique peut également être représentée sous la forme d’un logigramme de technologie électronique (ou pneumatique). Une fonction logique peut se décomposer en fonctions de base (opérateurs logiques). Il existe deux représentations graphiques normalisées pour ces dernières, l'une est Européenne, l'autre est Américaine. Le logigramme est la représentation graphique d’une fonction logique en combinant les symboles des opérateurs logiques qui la composent.

Pour notre exemple de système d’éclairage par va et vient* :*

A faire vous-même - Compléter le logigramme du va et vient :

Chronogramme :¶

Un chronogramme permet de décrire le fonctionnement d’un système au cours du temps. Une fonction logique peut donc être représentée par un chronogramme.

Il s’agit d’un graphe permettant de visualiser, en fonction du temps, l’état logique des sorties en fonction des états logiques pris par les entrées au cours du temps.

Pour notre exemple de système d’éclairage par va et vient* :*

A faire vous-même - Compléter le chronogramme du va et vient :

Algorithme :¶

Un algorithme est un ensemble de règles opératoires rigoureuses ordonnant, à un processeur particulier, d'exécuter dans un ordre déterminé, un nombre fini d'opérations élémentaires pour remplir une fonction donnée.

Un algorithme s'implémente dans un programme informatique.

L'algorithme est un outil méthodologique général qui ne doit pas être confondu avec le programme proprement dit.

Un algorithme peut être représenté :

soit graphiquement à l'aide de l'algorigramme (organigramme ou ordinogramme) en respectant un formalisme de symboles et de structure ;
soit littéralement grâce au langage algorithmique en respectant un formalisme d'écriture (pseudo-code).

Algorigramme :¶

C'est une représentation graphique de l'algorithme utilisant des symboles définis par des normes (NF Z 67-010 et ISO 5807)

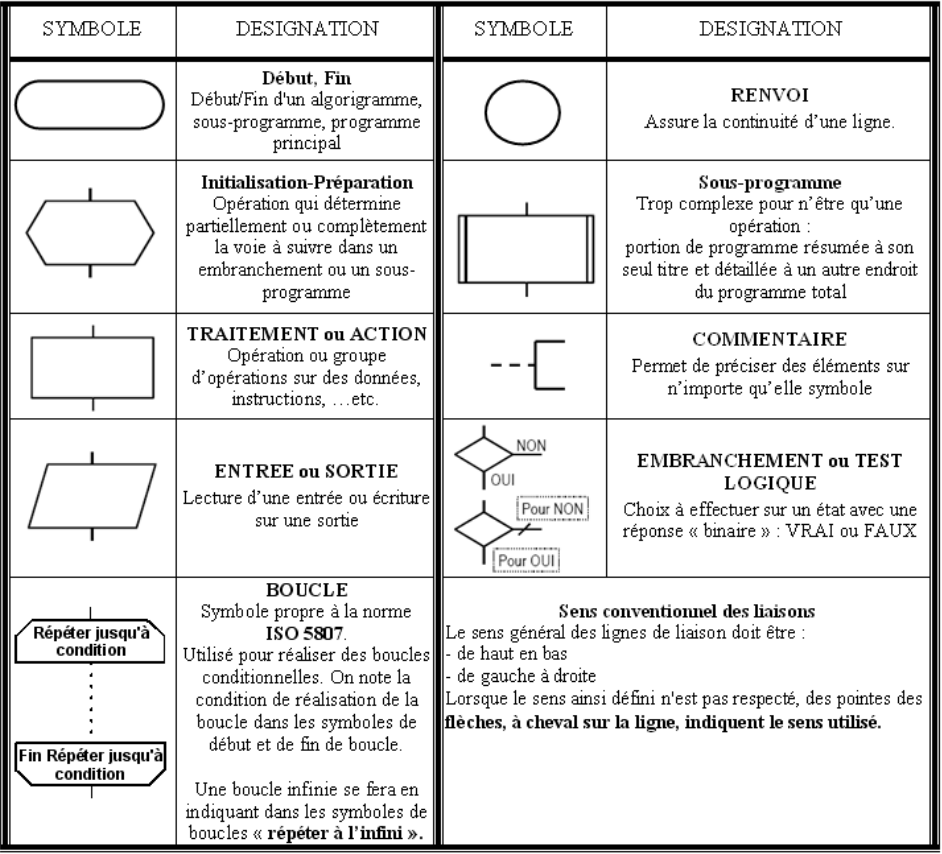
Pour notre exemple de système d’éclairage par va et vient* :*

A faire vous-même - Compléter l'algorigramme de la fonction va et vient :

Pseudo-Code :¶

Le pseudo-code est une façon de décrire un algorithme en langage presque naturel, sans référence à un langage de programmation en particulier.

Pour notre exemple de système d’éclairage par va et vient* :*

A faire vous-même - Compléter le pseudo-code de la fonction va et vient :
pseudo-code
TANT QUE Vrai
    FAIRE   
    LIRE a
    LIRE b
    SI ....................... = Vrai
    ALORS
       FAIRE
       L <- ....
    SINON
       FAIRE
       L <- ....
    FIN SI
    ECRIRE L
 FIN TANT QUE

Implémentation en Python :¶

En Python, une variable booléeene est soit True soit False et les opérateurs booléens sont les mots clés :

and pour le ET
or pour le OU
not pour le NON

Pour notre exemple de système d’éclairage par va et vient* :*

A faire vous-même - Compléter le script Python de la fonction va et vient :

Remarque : la fonction bool() renvoie True pour toute saisie input() non vide et False sinon.

In [ ]:

while True:
    a = bool(input())
    b = bool(input())
    if ............................. == True:
        L = .....
    else:
        L = .....
    print(L)

On observe que la fonction input() qui renvoie une chaine de caractères n'est pas très adaptée pour gérer des entrées booléennes même avec la fonction de conversion de type bool(). De plus, l'utilisation d'une boucle infinie n'est pas pratique...

Pour remédier, nous pouvons organiser notre code dans une fonction VaEtVient(a,b) et utiliser le module ipywidgets qui permet d'afficher une interface graphique interactive dans un carnet jupyter :

A faire vous-même - Compléter l'expression booléenne de la fonction VaEtVient(a,b) dans ce nouveau script Python :

In [ ]:

# Il faut importer la fonction interact() du module ipywidgets
from ipywidgets import interact

# Définition de la fonction logique à simuler
def VaEtVient(a, b):
    # Expression booléenne de la fonction en python
    L = ...........................
    # Résultat interactif à afficher
    return (print(f"Si a = {a} et b = {b} alors la lampe L = {L}"))

# Appel de la fonction interact() qui appelle la fonction logique à simuler
interact(VaEtVient, a = False, b = False)

Ce script peut être adapté pour toute autre fonction logique. Essayez...

SYSML, Diagramme d'Etats-Transitions (stm, State Machine Diagramme) :¶

Le diagramme d’états est un outil de la modélisation graphique SYSML qui permet de décrire le comportement dynamique séquentiel d’un système ou d'un sous-système. On parle alors d’une machine à états.

Le diagramme d'état décrit les transitions entre les états et les actions que le système ou ses parties réalisent en réponse à un événement.

Un état représente une période du fonctionnement du système pendant laquelle le système satisfait une certaine condition, accomplit une ou plusieurs actions, ou attend un évènement.

A un moment donné, un état est actif ou inactif. Plusieurs états peuvent être actifs simultanément.

Les états sont représentés par des rectangles aux coins arrondis.

On nomme transition le lien qui relie deux états successifs.

Depuis un état actif, pour activer un état lié, il faut que la condition de transition soit vérifée.

Actions dans un état : Pour définir les actions à exécuter il existe trois modes :

Actions à l’activation de l’état : la syntaxe est entry: action1, action2 ;
Action durant l’état : la syntaxe est during: action1, action2 ;
Action à la désactivation de l’état : la syntaxe est exit: action1, action2 ;

Pour notre exemple de système d’éclairage par va et vient* :*

A faire vous-même - Compléter le diagramme d'états-transitions de la fonction va et vient :

Références au programme :¶

Compétences développées	Connaissances associées
Traduire le comportement attendu ou observé d’un objet	Comportement séquentiel Structures algorithmiques (variables, fonctions, structures séquentielles, itératives, répétitives, conditionnelles) Diagramme d’états-transitions
Modéliser sous une forme graphique un circuit	Circuit électrique

Ce document est mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International.

Pour toute question, suggestion ou commentaire : eric.madec@ecmorlaix.fr

Logique de la chaine d'information :¶

Mise en situation :¶

Définition :¶

A faire vous-même - Compléter les entrées et sortie de la fonction traiter du va et vient :

Description d'une fonction logique¶

Proposition logique littérale :¶

Equation logique (Equation booléenne) :¶

A faire vous-même - Ecrire l'équation booléenne du va et vient :

Complément : les propriétés de l’algèbre de Boole ¶

Table de vérité :¶

A faire vous-même - Compléter la table de vérité du va et vient :

Tableau d'inventaire des principales fonctions logiques :¶

A faire vous-même :

Exemple de ressource du web :¶

Prolongement :

Lois de De Morgan :¶

Exercice d'application - Google doodle

Proposition de correction¶

Description d'une fonction logique (Suite) :¶

Schéma à contacts :¶

A faire vous-même - Tracer un schéma à contacts pour le va et vient :

Logigramme :¶

A faire vous-même - Compléter le logigramme du va et vient :

Chronogramme :¶

A faire vous-même - Compléter le chronogramme du va et vient :

Algorithme :¶

Algorigramme :¶

A faire vous-même - Compléter l'algorigramme de la fonction va et vient :

Pseudo-Code :¶

A faire vous-même - Compléter le pseudo-code de la fonction va et vient :

Implémentation en Python :¶

A faire vous-même - Compléter le script Python de la fonction va et vient :

A faire vous-même - Compléter l'expression booléenne de la fonction VaEtVient(a,b) dans ce nouveau script Python :

SYSML, Diagramme d'Etats-Transitions (stm, State Machine Diagramme) :¶

A faire vous-même - Compléter le diagramme d'états-transitions de la fonction va et vient :

Références au programme :¶

Logique de la chaine d'information :¶

Mise en situation :¶

Définition :¶

A faire vous-même - Compléter les entrées et sortie de la fonction traiter du va et vient :

Description d'une fonction logique¶

Proposition logique littérale :¶

Equation logique (Equation booléenne) :¶

A faire vous-même - Ecrire l'équation booléenne du va et vient :

Complément : les propriétés de l’algèbre de Boole¶

Table de vérité :¶

A faire vous-même - Compléter la table de vérité du va et vient :

Tableau d'inventaire des principales fonctions logiques :¶

A faire vous-même :

Exemple de ressource du web :¶

Prolongement :

Lois de De Morgan :¶

Exercice d'application - Google doodle

Proposition de correction¶

Description d'une fonction logique (Suite) :¶

Schéma à contacts :¶

A faire vous-même - Tracer un schéma à contacts pour le va et vient :

Logigramme :¶

A faire vous-même - Compléter le logigramme du va et vient :

Chronogramme :¶

A faire vous-même - Compléter le chronogramme du va et vient :

Algorithme :¶

Algorigramme :¶

A faire vous-même - Compléter l'algorigramme de la fonction va et vient :

Pseudo-Code :¶

A faire vous-même - Compléter le pseudo-code de la fonction va et vient :

Implémentation en Python :¶

A faire vous-même - Compléter le script Python de la fonction va et vient :

A faire vous-même - Compléter l'expression booléenne de la fonction VaEtVient(a,b) dans ce nouveau script Python :

SYSML, Diagramme d'Etats-Transitions (stm, State Machine Diagramme) :¶

A faire vous-même - Compléter le diagramme d'états-transitions de la fonction va et vient :

Références au programme :¶

Complément : les propriétés de l’algèbre de Boole ¶