Some important notes¶
- HW1 is out! Due January 25th at 11pm
- Homework will be submitted via Gradescope. Please see Piazza for precise instructions. Do it soon, not at the last minute!!
- There is an optional tutorial this evening, 5pm, in Dow 1013. Come see Daniel go over some tough problems.
- No class on Monday January 18, MLK day!
Python: We recommend Anacdona¶
 * Anaconda is standalone Python distribution that includes all the most important scientific packages: *numpy, scipy, matplotlib, sympy, sklearn, etc.*
* Easy to install, available for OS X, Windows, Linux.
* Small warning: it's kind of large (250MB)
* Anaconda is standalone Python distribution that includes all the most important scientific packages: *numpy, scipy, matplotlib, sympy, sklearn, etc.*
* Easy to install, available for OS X, Windows, Linux.
* Small warning: it's kind of large (250MB)
Some notes on using Python¶
- HW1 has only a very simple programming exercise, just as a warmup. We don't expect you to submit code this time
- This is a good time to start learning Python basics
- There are a ton of good places on the web to learn python, we'll post some
- Highly recommended: ipython; it's a much more user friendly terminal interface to python
- Even better: jupyter notebook, a web based interface. This is how I'm making these slides!
Checking if all is installed, and HelloWorld¶
If you got everything installed, this should run:
# numpy is crucial for vectors, matrices, etc.
import numpy as np
# Lots of cool plotting tools with matplotlib
import matplotlib.pyplot as plt
# For later: scipy has a ton of stats tools
import scipy as sp
# For later: sklearn has many standard ML algs
import sklearn
# Here we go!
print("Hello World!")
More on learning python¶
- We will have one tutorial devoted to this
- If you're new to Python, go slow!
- First learn the basics (lists, dicts, for loops, etc.)
- Then spend a couple days playing with numpy
- Then explore matplotlib
- etc.
- Piazza = your friend. We have a designated python instructor (IA Ben Bray) who has lots of answers.
Outline for this Lecture¶
- Convexity
- Convex Set
- Convex Function
- Introduction to Optimization
- Introduction to Lagrange Duality
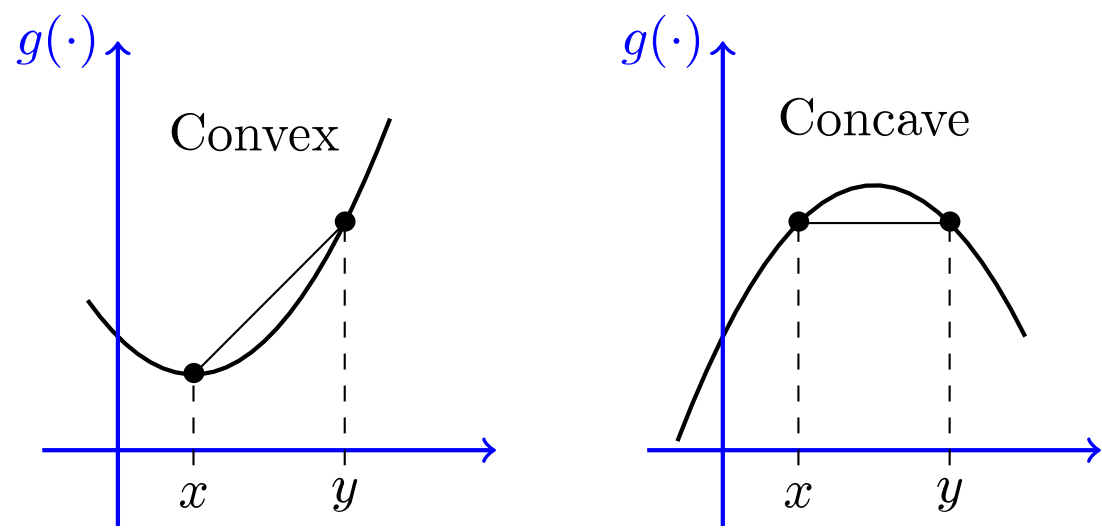
Convex Functions¶
- We say that a function $f$ is convex if, for any distinct pair of points $x,y$ we have
- A function $f$ is said to be concave if $-f$ is convex
Fun Facts About Convex Functions¶
- If $f$ is differentiable, then $f$ is convex iff $f$ "lies above its linear approximation", i.e.:
- If $f$ is twice-differentiable, then the hessian is always positive semi-definite!
- This last one you will show on your homeowork :-)
Introduction to Optimization¶
The Most General Optimization Problem¶
Assume $f$ is some function, and $C \subset \mathbb{R}^n$ is some set. The following is an optimization problem: $$ \begin{array}{ll} \mbox{minimize} & f(x) \\ \mbox{subject to} & x \in C \end{array} $$
- How hard is it to find a solution that is (near-) optimal? This is one of the fundamental problems in Computer Science and Operations Research.
- A huge portion of ML relies on this task
A Rough Optimization Hierarchy¶
$$ \mbox{minimize } \ f(x) \quad \mbox{subject to } x \in C $$- [Really Easy] $C = \mathbb{R}^n$ (i.e. problem is unconstrained), $f$ is convex, $f$ is differentiable, strictly convex, and "slowly-changing" gradients
- [Easyish] $C = \mathbb{R}^n$, $f$ is convex
- [Medium] $C$ is a convex set, $f$ is convex
- [Hard] $C$ is a convex set, $f$ is non-convex
- [REALLY Hard] $C$ is an arbitrary set, $f$ is non-convex
Optimization Without Constraints¶
$$ \begin{array}{ll} \mbox{minimize} & f(x) \\ \mbox{subject to} & x \in \mathbb{R}^n \end{array} $$- This problem tends to be easier than constrained optimization
- We just need to find an $x$ such that $\nabla f(x) = \vec{0}$
- Techniques like gradient descent or Newton's method work in this setting. (More on this later)
Optimization With Constraints¶
$$ \begin{aligned} & {\text{minimize}} & & f(\mathbf{x})\\ & \text{subject to} & & g_i(\mathbf{x}) \leq 0, \quad i = 1, ..., m\\ & & & h_j(x) = 0, \quad j = 1, ..., n \end{aligned} $$- Here $C = \{ x : g_i(x) \leq 0,\ h_j(x) = 0, \ i=1, \ldots, m,\ j = 1, ..., n \}$
- $C$ is convex as long as all $g_i(x)$ convex and all $h_j(x)$ affine
- The solution of this optimization may occur in the interior of $C$, in which case the optimal $x$ will have $\nabla f(x) = 0$
- But what if the solution occurs on the boundary of $C$?

Introduction to Lagrange Duality¶
- In some cases original (primal) optimization problem can hard to solve, solving a proxy problem sometimes can be easier
- The proxy problem could be dual problem which is transformed from primal problem
- Here is how to transform from primal to dual. For primal problem
Its Lagrangian is $$L(x,\boldsymbol{\lambda}, \boldsymbol{\nu}) := f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^n \nu_j h_j(x)$$ of which $\boldsymbol{\lambda} \in \mathbb{R}^m$, $\boldsymbol{\nu} \in \mathbb{R}^n$ are dual variables
- The Langragian dual function is
The minization is usually done by finding the stable point of $L(x,\boldsymbol{\lambda}, \boldsymbol{\nu})$ with respect to $x$
The Lagrange Dual Problem¶
- Then the dual problem is
Instead of solving primal problem with respect to $x$, we now need to solve dual problem with respect to $\mathbf{\lambda}$ and $\mathbf{\nu}$
- $ L_D(\mathbf{\lambda}, \mathbf{\nu})$ is concave even if primal problem is not convex
- Let the $p^*$ and $d^*$ denote the optimal values of primal problem and dual problem, we always have weak duality: $p^* \geq d^*$
- Under nice conditions, we get strong duality: $p^* = d^*$
- Many details are ommited here and they will come when we study support vector machine (SVM)


