ADI method, Elliptic, Parabolic PDEs

• Previously, the two dimensional, implicit parabolic PDE resulted in a penta-diagonal system of equations to solve at each point in time.
• A canonical elliptic equation is like a steady version of the parabolic equation:

$$\alpha\frac{\partial^2f}{\partial x^2} + \alpha\frac{\partial^2f}{\partial y^2} = S(x,y).$$

• Again, we define a two-dimensional grid and apply centered difference approximations to the derivatives.

$$\frac{\alpha}{\Delta x^2}(f_{i-1,j} - 2f_{i,j} + f_{i+1,j}) + \frac{\alpha}{\Delta y^2}(f_{i,j-1} - 2f_{i,j} + f_{i,j+1}) = S_{i,j}.$$

This is written in coefficient form as

$$uf_{i,j-1} + cf_{i-1,j} + af_{i,j} + cf_{i+1,j} + uf_{i,j+1} = b_{i,j}.$$

• When ordering the grid sequentially from left to right and top to bottom we obtain a penta-diagonal system of linear equations to solve.

Linear solution

• Direct methods:
  • This system could be solved with a purpose-built direct solver like an extention of the Thomas Algorithm.
• Iterative methods:
  • More common
  • Start with an initial guess of the solution, and iterate to convergence.
  • Jacobi, Gauss-Seidel, SOR
  • Conjugate Gradient method
  • Multigrid methods
  • Alternating direction implicit (ADI) method.

Alternating Direction Implicit (ADI)

• The Thomas Algorithm was fast and easy to implement.
• ADI is an iterative method, not unlike Gauss-Seidel, that arranges the unknowns in such a way that the system is tridagonal at each iteration step.
• There are two approaches

ADI 1

• Order the grid in two ways (A), and (B) (boundary points not shown):

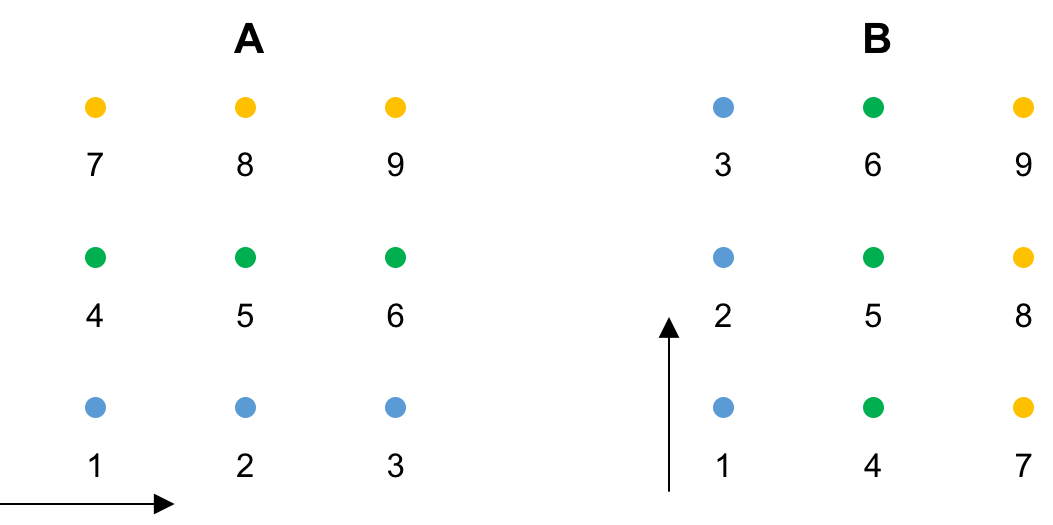* These 3x3 grids (9 unknowns) will result in 9x9 matrices.

• Grid (A), for any given point, the bottom and top neighbors are on diagonals -3 and 3.
  • Tridaigonal with $\pm j$ on off-diagonals -3 and 3.
  • In each equation move $y$-directed neighbors to the RHS of the equation and use previous values to evaluate them.

• Grid (B), for any given point, the left and right neighbors are on diagonals -3 and 3.
  • Tridaigonal with $\pm i$ on off-diagonals -3 and 3.
  • In each equation move $x$-directed neighbors to the RHS of the equation and use previous values to evaluate them.

* **Alternate the grids.** Each iteration solves Grid (A) then Grid (B). Iterate to convergence.

ADI 2

• Instead of considering the whole 9x9 system, we treat the 2-D grid as a sequence of 1-D problems.
  • We sweep the grid in the y-direction, then the x-direction.

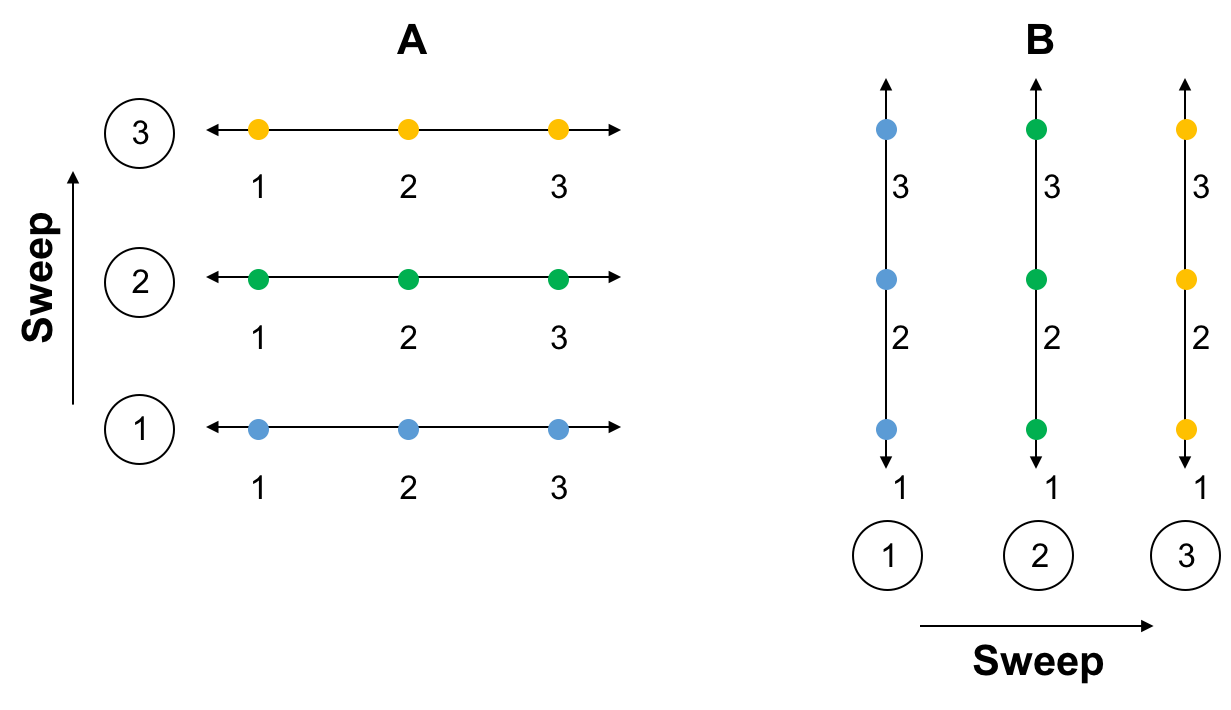
• Grid A
  • For line (1), we form a tridiagonal system with points (1), (2), and (3) as the unknowns.
    • That is, points $f_{1,1}$, $f_{1,2}$, $f_{1,3}$ are the unknowns.
    • All other points in the 2-D, 5-point stencil are considered known.
    • This gives a 3x3 tridiagonal matrix for the grid shown.
    • We solve this system and update the three points.
  • Repeat this for line (2), then line (3).
  • Note that we are coupling the x-direction points and decoupling the y-direction points.

• Grid B

  • Follow the same approach as in Grid A.
  • But now, we are coupling the y-direction points and decoupling the x-direction points.

• One iteration consists of sweeping lines (1), (2), and (3) on Grid A, followed by sweeping lines (1), (2), and (3) on Grid B.

• Matricies are setup in the usual fashion, with decoupled points on the RHS, and boundary conditions properly specified.

Notes

• ADI 1 is more matrix-specific
• ADI 2 is more grid-specific
• Note how these ADI methods fully couple one dimension at a time allowing full information propagation in the given direction.
• The pentadiagonal solve only requires one iteration.
• The Gauss-Seidel method decouples both directions, so information propagates more slowly across the domain.
• The ADI is in-between.

• In 3-D we have a heptadiagonal system with three grids.
  • For ADI 1, we again move four of the seven off diagonals to the RHS, and alternate between the grid ordering.
  • For ADI 2, we sweep lines in the x, y, and z directions sequentially.
• Elliptic methods are very common, but often occur as parts of larger problems.
  • In fluid mechanics, the pressure Poisson equation is an example.
• All of this applies to implicit parabolic problems such as the BTCS and CN methods.

Hoffman version

• For parabolic problems, Hoffman gives an ADI alternative.

  • Rather than converge the ADI algorithm at each timestep, (since we have a $\Delta t$ truncation error anyway), we can solve as follows:

  $$\frac{\color{blue}{f_{i,j}^{n+1}}-f_{i,j}^n}{\Delta t} = \alpha\color{blue}{\left(\frac{\partial^2f}{\partial x^2}\right)_{i,j}^{n+1} + } \alpha\left(\frac{\partial^2f}{\partial y^2}\right)_{i,j}^n + S_{i,j}^n,$$

  $$\frac{\color{blue}{f_{i,j}^{n+2}}-f_{i,j}^{n+1}}{\Delta t} = \alpha\left(\frac{\partial^2f}{\partial x^2}\right)_{i,j}^{n+1} + \alpha\color{blue}{\left(\frac{\partial^2f}{\partial y^2}\right)_{i,j}^{n+2}} + S_{i,j}^{n+1}.$$

  • On one timestep we implicitly couple the x-direction and the y-direction is decoupled (explicit).
  • On the next timestep, we implicitly couple the y-direction and the x-direction is decoupled (explicit).