Le Bloc Note pour apprendre à coder en hexadécimal :¶

Nous savons maintenant que de nos jours les ordinateurs comme pratiquement tous les systèmes numériques communiquent en faisant circuler des informations sous la forme de mots binaires à 8 bits = 1 octet que l'on nomme bytes même si cela n'a pas toujours été le cas : https://fr.wikipedia.org/wiki/Byte.

Pour un humain (normalement constitué), il est fastidieux d'écrire ou de déchiffré à la volée de telles trames d'informations directement au format binaire :

0100111001010011010010010010110000100000011000110010011101100101011100110111010000100000011000110110111101101111011011000010000000100001

Le format hexadécimal présente de façon plus condensée un message binaire constitué d'une suite d'octects.

Système hexadécimal :¶

C’est un système de base $16$ qui utilise donc seize symboles différents :

$$ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F$$

Pour distinguer un nombre hexadécimal on indique le code 0x (ou le symbole #) avant le nombre ou l’indice $_{16}$ (ou $_h$) après le nombre.

Les lettres A à F correspondent respectivement au nombre décimaux ? $10, 11, 12, 13, 14, 15$

$AC53_{16}$ = $10 \times 16^3 + 12 \times 16^2 + 5 \times 16^1 + 3 \times 16^0$

Correspondance entre nombres de différentes bases :¶

Changement de base :¶

Conversion d’un nombre hexadécimal en binaire.¶

Chaque symbole du nombre écrit dans le système hexadécimal est remplacé par son équivalent écrit dans le système binaire.

Exemple : Convertir $ECA_{16}$ = ${1110_2\over E_{16}}{1100_2\over C_{16}}{1010_2\over A_{16}}$ = $1110 1100 1010_2$

Conversion d’un nombre binaire en hexadécimal.¶

C’est l’inverse de la précédente. Il faut donc regrouper les 1 et les 0 du nombre par 4 en commençant par la droite, quitte à rajouter des 0 à gauche, puis chaque groupe est remplacé par le symbole hexadécimal correspondant.

Exemple : Convertir $1100001101111_2$ = ${1_{16}\over 0001_2}{8_{16}\over 1000_2}{6_{16}\over 0110_2}{F_{16}\over 1111_2}$ = $186F_{16}$

A faire vous même n°1 :

Recoder en hexadécimal la trame d'information binaire donnée au début de ce notebook.

A faire vous même n°2 :

L'objectif de cet exercice est de convertir des nombres entiers donnés en décimal, en binaire ou en héxadécimal, pour dessiner une image matricielle dans un quadrillage $8 \times 8$.

Chaque case de l'image correspond à un bit. Une ligne de l'image fait 8 cases, soit 8 bits ou 1 octet.

Lorsque le bit est à 1 alors la case est noire, lorsque le bit est à 0 alors la case est blanche.

Exemple :¶

A faire vous même : compléter le quadrillage pour découvrir l'image...¶

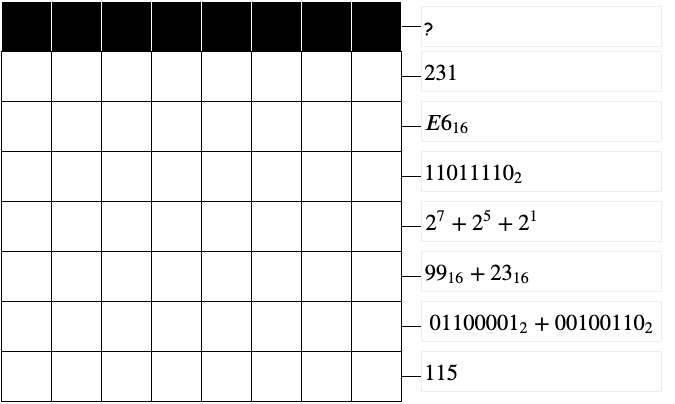
Vérification :¶

Un moyen de vérifer si on n'a pas fait d'erreur est de fournir un nombre qui pourrait être un code de validation.

Cette méthode n'est pas fiable à 100% mais elle permet très souvent de savoir si une erreur a été commise.

Pour chaque colonne, on compte le nombre de 1 ; si ce nombre est pair, on marque 0 ; s'il est impair, on marque 1. On obtient ainsi un nombre 8 bits (1 pour chaque colonne).

Le code de validation de l'image ci-dessus est égal à 202. Utilisez-le pour valider votre codage.

Fonctions de conversion de Python :¶

La fonction bin() permet de convertir un nombre en binaire :

In [ ]:

bin(91)

In [ ]:

bin(0x5b)

La fonction hex() permet de convertir un nombre en hexadécimal :

In [ ]:

hex(91)

In [ ]:

hex(0b1011011)

La fonction int() permet de convertir un nombre en décimal :

In [ ]:

int(0b1111010111)

In [ ]:

int(0x5b)

Codage Hexadécimal des couleurs :¶

Les couleurs RVB peuvent être exprimées dans différents formats comme : (34,255,67) ou #90FF56.

(34,255,67) indique les composantes Rouge=34, Vert=255, Bleu=67 avec des nombres en base 10.

Tandis que #90FF56 indique Rouge=90, Vert=FF, Bleu=56 en base 16.

Le préfixe # indique seulement qu'il s'agit d'une écriture hexadécimale.

A faire vous même n°3 :

Les deux codes proposés ci-dessus, (34,255,67) et #90FF56, représentent-ils la même couleur ?

.....................................................

Vérifiez votre réponse avec le module ipythonblocks et son sélectionneur de couleur intégré :

Sur iPad, vérifier si le module ipythonblocks est déjà installé :

%pip list

Sinon il faut l'installer en faisant :

%pip install ipythonblocks

In [1]:

from ipythonblocks import show_color, embed_colorpicker

In [7]:

show_color(200,100,50)

In [3]:

embed_colorpicker()

Pour plus d'information sur les couleurs utilisées en HTML :

https://htmlcolorcodes.com/fr/selecteur-de-couleur/

A faire vous même n°4 :

On observe que le module ipythonbloks ne prend pas les codes couleurs au format hexadécimal. Nous aurions donc besoin d'une fonction python qui prenne en entrée une chaine de caractères correspondante au code hexadécimal d'une couleur et qui renvoie son code convertit au format décimal dans une chaine de caractères en sortie...

Références aux programmes :¶

Compétences développées	Capacités attendues	Commentaires
Écriture d’un entier positif dans une base b ⩾ 2	Passer de la représentation d’une base dans une autre.	Les bases 2, 10 et 16 sont privilégiées.

Ce document est mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International.

Pour toute question, suggestion ou commentaire : eric.madec@ecmorlaix.fr