Chaine d'information d'un système¶

Analyse fonctionnelle et structurelle¶

Dans un système pluritechnique, la chaine d'information permet :

d'acquérir des informations en provenance de lui même, d'autres systèmes connectés, et de son utilisateur par l'intermédiaire d'une interface homme/machine (IHM) ;
de les traiter pour contrôler l'action à réaliser sur la matière d'oeuvre ;
et de communiquer l'état du système à l'utilisateur ou à d'autres systèmes connectés.

Exemple du Stepper :¶

Liens drawio :

La fonction "Acquérir" :¶

L'acquisition de grandeurs physiques se fait par l'intermédiaires de capteurs. Un capteur est un composant qui convertit une grandeur physique en un signal exploitable par l'unité de traitement*.

Exemples de capteurs de grandeur physique :

- sur le stepper... ? ;
- autres... ?.

L'acquisition des consignes de l'utilisateur se fait par l'intermédiaire d'une interface homme/machine (IHM) qui intègre des composants capables de convertir des informations humaines en un signal exploitable par l'unité de traitement*.

Exemples de composants d'IHM :

- sur le stepper... ? ;
- autres... ?.

Un signal exploitable par l'unité de traitement : très souvent ce signal sera de nature électrique, rendu compatible avec le microcontroleur utilisé pour le traitement de l'information...

Typologie des signaux logique, analogique et numérique :¶

Source : www.lossendiere.com

Ressource vidéo :¶

In [19]:

%%HTML
<center>
<iframe width="560" height="315" src="https://www.youtube-nocookie.com/embed/2PckTQZTdBw?start=16" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
</center>

Numération et codage de l’information, changement de base¶

Problématique :¶

Dans notre exemple du stepper, l'information fournie à l'entrée de la chaine par le capteur ILS est de type logique (Tout ou Rien TOR, $0$ ou $1$) or le système de numération adapté pour traiter ce genre d'information est le binaire (à base $2$).

Par conntre, en sortie, l'information à afficher est destinée à l'utilisateur qui lui compte avec un système de numération décimal (à base $10$).

Plus généralement, on le reverra en détail plus tard, lorsque la grandeur physique à acquérir sera de type analogique, il nous faudra la numériser pour la traiter avec un microcontrôleur.

On peut donc d'ores et déjà affirmer que les données qui circuleront dans la chaine d'information seront, à un endroit ou à un autre, numériques (ou pour le moins logique) même si elles représentent autre chose.

Aussi, pour bien comprendre le codage de l'information qui circulent nous devons être capable de convertir une donnée numérique d'un système de numération à l'autre...

Les bases :¶

Système décimal :¶

C’est le système de numération que nous utilisons tous les jours. C’est un système de base $10$ car il utilise dix symboles différents : $$ 0,..$$

C’est un système positionnel car l’endroit où se trouve le symbole dans le nombre définit sa valeur. Le $2$ du nombre décimal $2356$ n’a pas la même valeur celui du nombre décimal $5623$ :

$2356 = 2 \times 10^3 + 3 \times 10^2 + 5 \times 10^1 + 6 \times 10^0$ ici le $2$ vaut $2000$

$5623 = ..........................................?$ ici le $2$ vaut $?$

Système binaire :¶

C’est le système de numération utilisé par les « machines numériques ». C’est un système de base $2$ car il utilise deux symboles différents : $$ 0,..$$

Pour distinguer le nombre binaire 10110 du nombre décimal 10110 on indique le code 0b (ou le symbole %) avant le nombre ou l’indice $_2$ (ou $_b$) après le nombre.

$10110_2$ =

On appel bit (contraction de Binary digIT = BIT) chacun des chiffres d’un nombre binaire.

Avec un bit on peut distinguer deux états d’une information avec les deux nombres soit $1$, soit $0$.

Avec $2$ bits ?

Avec $3$ bits ?

Avec $8$ bits ?

Avec n bits on peut former ? combinaisons (nombres) différentes.

Une suite de quatre bits est un ? , une suite de huit bits est un ?

Une suite de 16, 32, 64 bits est un ?

Système hexadécimal.¶

C’est un système de base $16$ qui utilise donc seize symboles différents :

$$ 0,..$$

Pour distinguer un nombre hexadécimal on indique le code 0x (ou le symbole $) avant le nombre ou l’indice $_{16}$ (ou $_h$) après le nombre.

Les lettres A à F correspondent respectivement au nombre décimaux ?

$AC53_{16}$ = ...........?

Correspondance entre nombres de différentes bases :¶

Changement de base :¶

Conversion d’un nombre décimal en un nombre d’une autre base¶

Une méthode de conversion consiste à décomposer le nombre décimal en une somme de puissances de deux.

Par exemple, pour la conversion : $91$ = $01011011_2$

On peut écrire : $$91 = 0 \times 2^7 + 1 \times 2^6 + 0 \times 2^5 + 1 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0$$
$$91 = 64 + 16 + 8 + 2 + 1$$
En rangeant les puissances de deux dans un tableau, on obtient :

Une autre méthode de conversion consiste à diviser le nombre décimal à convertir par la base b et conserver le reste de la division. Le quotient obtenu est divisé par b et conserver le reste. Il faut répéter l’opération sur chaque quotient obtenu.

Par exemple, pour la conversion : $91$ = $01011011_2$

Les restes successifs sont écrits, en commençant par le dernier, de la gauche vers la droite. Cette méthode est dite « Méthode des divisions successives ».

Conversion d’un nombre hexadécimal en binaire.¶

Chaque symbole du nombre écrit dans le système hexadécimal est remplacé par son équivalent écrit dans le système binaire.

Exemple : Convertir $ECA_{16}$ = ${1110_2\over E_{16}}{1100_2\over C_{16}}{1010_2\over A_{16}}$ = $1110 1100 1010_2$

Conversion d’un nombre binaire en hexadécimal.¶

C’est l’inverse de la précédente. Il faut donc regrouper les 1 et les 0 du nombre par 4 en commençant par la droite, puis chaque groupe est remplacé par le symbole hexadécimal correspondant.

Exemple : Convertir $1100001101111_2$ = ${1_{16}\over 0001_2}{8_{16}\over 1000_2}{6_{16}\over 0110_2}{F_{16}\over 1111_2}$ = $186F_{16}$

Exercices :¶

Convertir $9F2_{16}$ en binaire.

Convertir $001111110101_2$ en hexadécimal.

Convertir en décimal les nombres binaires suivants : $10110_2$ ; $10001101_2$ ; $1111010111_2$

Convertir en binaire les nombres décimaux suivants : $37$ ; $189$ ; $205$ ; $2313$.

Convertir en décimal les nombres hexadécimaux suivants : $92_{16}$ ; $2C0_{16}$ ; $37FD_{16}$.

Convertir en hexadécimal les nombres décimaux suivants : 75 ; 314 ; 25619.

Quelle est l’étendue des nombres définis en hexadécimal sur 6 chiffres ?

Exécuter les opérations $10111101_2 + 101111_2$, $1BF_{16} + A23_{16}$

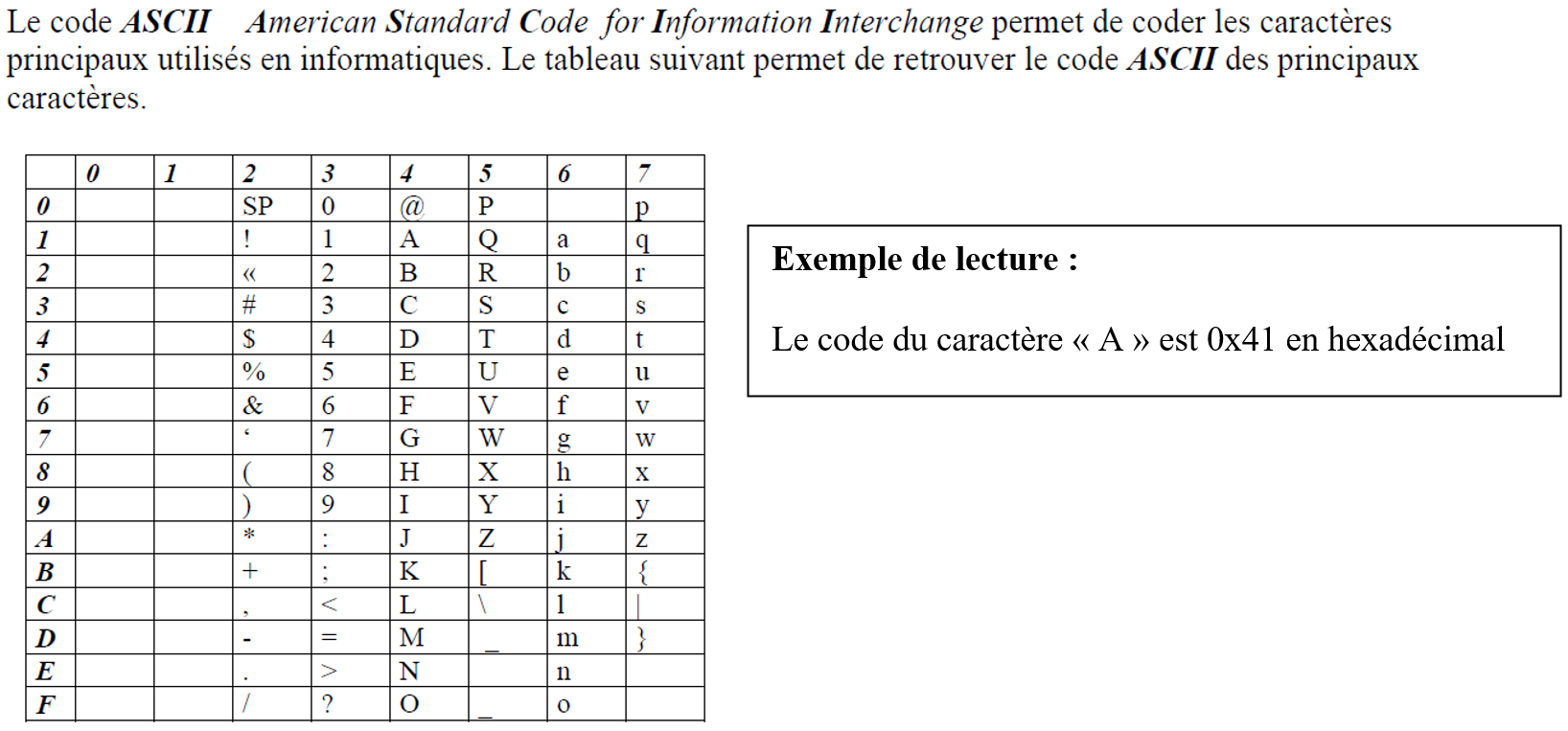
Quel est le code ASCII en hexadécimal correspondant à la chaine de caractères 1SI ?

Vérification avec Python :¶

La fonction bin() permet de convertir un nombre en binaire :

In [ ]:

bin(91)

In [ ]:

bin(0x5b)

La fonction hex() permet de convertir un nombre en hexadécimal :

In [ ]:

hex(91)

In [ ]:

hex(0b1011011)

La fonction int() permet de convertir un nombre en décimal :

In [ ]:

int(0b1011011)

In [ ]:

int(0x5b)

Ressources :¶

In [1]:

%%HTML
<center>
    <iframe src="https://player.vimeo.com/video/100900776?byline=0&portrait=0" width="640" height="480" frameborder="0" allow="autoplay; fullscreen" allowfullscreen></iframe>
<p><a href="https://vimeo.com/100900776">Binary and Decimal Conversion</a> from <a href="https://vimeo.com/user30149681">EICC</a> on <a href="https://vimeo.com">Vimeo</a>.</p>
</center>

Binary and Decimal Conversion from EICC on Vimeo.

Références au programme :¶

Compétences développées	Connaissances associées
Caractériser les échanges d’informations	Natures et caractéristiques des signaux, des données, des supports de communication...

Ce document est mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International.

Pour toute question, suggestion ou commentaire : eric.madec@ecmorlaix.fr