Title: Two Years of Bayesian Bandits for E-Commerce
Abstract: At Monetate, we've deployed Bayesian bandits (both noncontextual and contextual) to help our clients optimize their e-commerce sites since early 2016. This talk is an overview of the lessons we've learned from both the processes of deploying real-time Bayesian machine learning systems at scale and building a data product on top of these systems that is accessible to non-technical users (marketers). This talk will cover
- the place of multi-armed bandits in the A/B testing industry,
- Thompson sampling and the basic theory of Bayesian bandits,
- Bayesian approaches for accommodating nonstationarity in bandit feedback,
- user experience challenges in driving adoption of these technologies by nontechnical marketers.
We will focus primarily on noncontextual bandits and give a brief overview of these problems in the contextual setting as time permits.
Bio: Austin Rochford is Chief Data Scientist at Monetate, where he does research and development for machine learning-driven marketing products. He is a recovering mathematician, a passionate Bayesian, and a PyMC3 developer.
A Dockerfile that will produce a container with the dependenceis of this notebook is available here.
%matplotlib inline
from tqdm import tqdm, trange
from matplotlib import pyplot as plt
from matplotlib.dates import DateFormatter, MonthLocator
from matplotlib.ticker import StrMethodFormatter
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
SEED = 76224 # from random.org, for reproducibiliy
np.random.seed(SEED)
sns.set()
C = sns.color_palette()
pct_formatter = StrMethodFormatter('{x:.1%}')
#configure matplotlib
FIGURE_WIDTH = 8
FIGURE_HEIGHT = 6
plt.rc('figure', figsize=(FIGURE_WIDTH, FIGURE_HEIGHT))
LABELSIZE = 14
plt.rc('axes', labelsize=LABELSIZE)
plt.rc('axes', titlesize=LABELSIZE)
plt.rc('figure', titlesize=LABELSIZE)
plt.rc('legend', fontsize=LABELSIZE)
plt.rc('xtick', labelsize=LABELSIZE)
plt.rc('ytick', labelsize=LABELSIZE)
Two Years of Bayesian Bandits for E-Commerce¶

NYC College of Technology • April, 18 2019 • @AustinRochford¶
About Me¶
 |
 |
Chief Data Scientist, Monetate¶
@AustinRochford • austinrochford.com • github.com/AustinRochford¶
arochford@monetate.com • austin.rochford@gmail.com¶
About Monetate¶

- Founded 2008, web optimization and personalization SaaS
- Observed 5B impressions and $4.1B in revenue during Cyber Week 2017
Non-technical marketer-focused¶
About this talk¶
Outline¶
- Web optimization
- A/B testing
- Multi-armed bandits
- Bayesian bandits
- Thompson sampling
- Bandit bias
- Inverse propensity weighting
A/B testing machinery¶

|

|
Sequential testing¶

|

|
Sequential optimization¶

Much of the A/B testing industry uses classical Fisher/Neyman-Pearson style fixed-horizon frequentist significance tests. Sophistocated approaches use sequential hypothesis testing. We've found, through many years of interaction with marketers, that they take a fundamentally Bayesian view of the world. Most interpret p-values as the "probability that the experiment is better/worse than the control."
Multi-armed bandits¶

Multi-armed bandit problems are extensively studied and come in many variantions. Here we focus on the simplest multi-armed bandit objective, regret minimization.
Multi-armed bandit systems¶
Bayesian Bandits¶
Beta-binomial model¶
$$ \begin{align*} x_A, x_B & = \textrm{number of rewards from users shown variant } A, B \\ x_A & \sim \textrm{Binomial}(n_A, r_A) \\ x_B & \sim \textrm{Binomial}(n_B, r_B) \\ r_A, r_B & \sim \textrm{Beta}(1, 1) \end{align*} $$Thompson sampling¶
Thompson sampling randomizes user/variant assignment according to the probabilty that each variant maximizes the posterior expected reward.
The probability that a user is assigned variant A is
$$ \begin{align*} P(r_A > r_B\ |\ \mathcal{D}) & = \int_0^1 P(r_A > r\ |\ \mathcal{D})\ \pi_B(r\ |\ \mathcal{D})\ dr \\ & = \int_0^1 \left(\int_r^1 \pi_A(s\ |\ \mathcal{D})\ ds\right)\ \pi_B(r\ |\ \mathcal{D})\ dr \\ & \propto \int_0^1 \left(\int_r^1 s^{\alpha_A - 1} (1 - s)^{\beta_A - 1}\ ds\right) r^{\alpha_B - 1} (1 - r)^{\beta_B - 1}\ dr \end{align*} $$Monte Carlo Methods¶
N = 5000
x, y = np.random.uniform(0, 1, size=(2, N))
fig, ax = plt.subplots()
ax.set_aspect('equal');
ax.scatter(x, y, c='k', alpha=0.5);
ax.set_xticks([0, 1]);
ax.set_xlim(0, 1.01);
ax.set_yticks([0, 1]);
ax.set_ylim(0, 1.01);
fig
in_circle = x**2 + y**2 <= 1
fig, ax = plt.subplots()
ax.set_aspect('equal');
x_plot = np.linspace(0, 1, 100)
ax.plot(x_plot, np.sqrt(1 - x_plot**2), c='k');
ax.scatter(x[in_circle], y[in_circle], c='g', alpha=0.5);
ax.scatter(x[~in_circle], y[~in_circle], c='r', alpha=0.5);
ax.set_xticks([0, 1]);
ax.set_xlim(0, 1.01);
ax.set_yticks([0, 1]);
ax.set_ylim(0, 1.01);
fig
4 * in_circle.mean()
3.1743999999999999
fig, ax = plt.subplots(
figsize=(0.75 * FIGURE_WIDTH, 0.75 * FIGURE_WIDTH)
)
ax.set_aspect('equal');
a_post = sp.stats.beta(5 + 1, 15 + 1)
b_post = sp.stats.beta(7 + 1, 13 + 1)
p = np.linspace(0, 1, 100)
px, py = np.meshgrid(p, p)
z = a_post.pdf(px) * b_post.pdf(py)
ax.contourf(px, py, z, 1000, cmap='BuGn');
ax.plot([0, 1], [0, 1], c='k', ls='--');
ax.xaxis.set_major_formatter(pct_formatter);
ax.set_xlabel(r"$r_A \sim \operatorname{Beta}(6, 16)$");
ax.yaxis.set_major_formatter(pct_formatter);
ax.set_ylabel(r"$r_B \sim \operatorname{Beta}(8, 14)$");
ax.set_title("Posterior reward rates");
fig
%%time
N_SAMPLES = 10000
a_samples = a_post.rvs(size=N_SAMPLES)
b_samples = b_post.rvs(size=N_SAMPLES)
CPU times: user 0 ns, sys: 10 ms, total: 10 ms Wall time: 9.12 ms
a_samples_ = a_samples[::5]
b_samples_ = b_samples[::5]
ax.scatter(
a_samples_[b_samples_ > a_samples_],
b_samples_[b_samples_ > a_samples_],
c='C0', alpha=0.25
);
ax.scatter(
a_samples_[b_samples_ < a_samples_],
b_samples_[b_samples_ < a_samples_],
c='C1', alpha=0.25
);
fig
ts_fig = fig
(a_samples > b_samples).mean()
0.2457
Thompson sampling, redeemed¶
- Sample $\hat{r}_A \sim r_A\ |\ n_A, x_A$ and $\hat{r}_B \sim r_B\ |\ n_B, x_B$.
- Assign the user variant A if $\hat{r}_A > \hat{r}_B$, otherwise assign them variant B.
Simulating a bandit¶
class BetaBinomial:
def __init__(self, a0=1., b0=1.):
self.a = a0
self.b = b0
def sample(self):
return sp.stats.beta.rvs(self.a, self.b)
def update(self, n, x):
self.a += x
self.b += n - x
class Bandit:
def __init__(self, a_post, b_post):
self.a_post = a_post
self.b_post = b_post
def assign(self):
return 1 * (self.a_post.sample() < self.b_post.sample())
def update(self, arm, reward):
arm_post = self.a_post if arm == 0 else self.b_post
arm_post.update(1, reward)
def generate_rewards(a_rate, b_rate, n):
yield from zip(
np.random.binomial(1, a_rate, size=n),
np.random.binomial(1, b_rate, size=n)
)
A_RATE, B_RATE = 0.05, 0.1
N = 1000
rewards_gen = generate_rewards(A_RATE, B_RATE, N)
bandit = Bandit(BetaBinomial(), BetaBinomial())
arms = np.empty(N, dtype=np.int64)
rewards = np.empty(N)
for t, arm_rewards in tqdm(enumerate(rewards_gen), total=N):
arms[t] = bandit.assign()
rewards[t] = arm_rewards[arms[t]]
bandit.update(arms[t], rewards[t])
100%|██████████| 1000/1000 [00:00<00:00, 4504.52it/s]
fig, (regret_ax, assign_ax) = plt.subplots(
ncols=2, sharex=True,
figsize=(2 * FIGURE_WIDTH, 6)
)
plot_t = np.arange(N) + 1
regret_ax.plot(
plot_t, rewards.cumsum(),
c=C[0], label="Bandit"
);
regret_ax.plot(
plot_t, A_RATE * plot_t,
c=C[1], ls='--',
label="Variant A"
);
regret_ax.plot(
plot_t, B_RATE * plot_t,
c=C[2], ls='--',
label="Variant B"
);
regret_ax.plot(
plot_t,
0.5 * (A_RATE + B_RATE) * plot_t,
c='k', ls='--',
label="A/B testing"
);
regret_ax.set_xlim(1, N);
regret_ax.set_xlabel("Sessions");
regret_ax.set_ylabel("Rewards");
regret_ax.legend(loc=2);
assign_ax.plot(plot_t, (arms == 1).cumsum() / plot_t);
assign_ax.hlines(
0.5, 1, N,
colors='k', linestyles='--'
);
assign_ax.set_xlabel("Sessions");
assign_ax.set_ylim(0, 1);
assign_ax.yaxis.set_major_formatter(pct_formatter);
assign_ax.set_yticks(np.linspace(0, 1, 5));
assign_ax.set_ylabel("Traffic shown variant B");
fig.suptitle("Cumulative bandit performance");
fig
Simulating many bandits¶
def simulate_bandit(rewards, n,
progressbar=False,
prior=BetaBinomial):
bandit = Bandit(prior(), prior())
arms = np.empty(n, dtype=np.int64)
obs_rewards = np.empty(n)
if progressbar:
rewards = tqdm(rewards, total=n)
for t, arm_rewards in enumerate(rewards):
arms[t] = bandit.assign()
obs_rewards[t] = arm_rewards[arms[t]]
bandit.update(arms[t], obs_rewards[t])
return arms, obs_rewards
N_BANDIT = 100
arms = np.empty((N_BANDIT, N), dtype=np.int64)
rewards = np.empty((N_BANDIT, N))
for i in trange(N_BANDIT):
arms[i], rewards[i] = simulate_bandit(
generate_rewards(A_RATE, B_RATE, N), N
)
100%|██████████| 100/100 [00:13<00:00, 7.93it/s]
fig, (regret_ax, assign_ax) = plt.subplots(
ncols=2, sharex=True,
figsize=(2 * FIGURE_WIDTH, 6)
)
plot_t = np.arange(N) + 1
cum_rewards = rewards.cumsum(axis=1)
ALPHA = 0.1
low_rewards, high_rewards = np.percentile(
cum_rewards, [100 * ALPHA / 2, 100 * (1 - ALPHA / 2)],
axis=0
)
regret_ax.fill_between(
plot_t, low_rewards, high_rewards,
color=C[0], alpha=0.5,
label=f"{1 - ALPHA:.0%} interval"
);
regret_ax.plot(
plot_t, cum_rewards.mean(axis=0),
c=C[0], label="Bandit (average)"
);
regret_ax.plot(
plot_t, A_RATE * plot_t,
c=C[1], ls='--',
label="Variant A"
);
regret_ax.plot(
plot_t, B_RATE * plot_t,
c=C[2], ls='--',
label="Variant B"
);
regret_ax.plot(
plot_t,
0.5 * (A_RATE + B_RATE) * plot_t,
c='k', ls='--',
label="A/B testing"
);
regret_ax.set_xlim(1, N);
regret_ax.set_xlabel("Sessions");
regret_ax.set_ylabel("Rewards");
regret_ax.legend(loc=2);
cum_winner = (arms == 1 * (A_RATE < B_RATE)).cumsum(axis=1)
low_winner, high_winner = np.percentile(
cum_winner / plot_t, [100 * ALPHA / 2, 100 * (1 - ALPHA / 2)],
axis=0
)
assign_ax.fill_between(
plot_t, low_winner, high_winner,
color=C[0], alpha=0.5,
label=f"{1 - ALPHA:.0%} interval"
);
assign_ax.plot(plot_t, cum_winner.mean(axis=0) / plot_t);
assign_ax.hlines(
0.5, 1, N,
colors='k', linestyles='--'
);
assign_ax.set_xlabel("Sessions");
assign_ax.set_ylim(0, 1);
assign_ax.yaxis.set_major_formatter(pct_formatter);
assign_ax.set_yticks(np.linspace(0, 1, 5));
assign_ax.set_ylabel("Traffic shown better variant");
fig.suptitle(f"Cumulative bandit performance ({N_BANDIT} simulations)");
fig
A/A testing¶

A/A bandits¶
def simulate_bandits(rewards_factory, n, n_bandit,
progressbar=True,
prior=BetaBinomial):
arms = np.empty((n_bandit, n), dtype=np.int64)
rewards = np.empty((n_bandit, n))
if progressbar:
bandits_range = trange(n_bandit)
else:
bandits_range = range(n_bandit)
for i in bandits_range:
arms[i], rewards[i] = simulate_bandit(
rewards_factory(), n,
prior=prior
)
return arms, rewards
N = 2000
arms, rewards = simulate_bandits(
lambda: generate_rewards(A_RATE, A_RATE, N),
N, N_BANDIT
)
100%|██████████| 100/100 [00:26<00:00, 4.76it/s]
fig, ax = plt.subplots()
plot_t = np.arange(N) + 1
cum_winner = (arms == 0).cumsum(axis=1)
low_winner, high_winner = np.percentile(
cum_winner / plot_t, [100 * ALPHA / 2, 100 * (1 - ALPHA / 2)],
axis=0
)
ax.fill_between(
plot_t, low_winner, high_winner,
color=C[0], alpha=0.5,
label=f"{1 - ALPHA:.0%} interval"
);
ax.plot(
plot_t, cum_winner.mean(axis=0) / plot_t,
label="Bandit (average)"
);
ax.hlines(
0.5, 1, N,
colors='k', linestyles='--'
);
ax.set_xlim(1, N);
ax.set_xlabel("Sessions");
ax.set_ylim(0, 1);
ax.yaxis.set_major_formatter(pct_formatter);
ax.set_yticks(np.linspace(0, 1, 5));
ax.set_ylabel("Traffic shown variant A");
ax.legend(loc=2)
ax.set_title(f"Cumulative bandit performance ({N_BANDIT} simulations)");
fig
fig, ax = plt.subplots()
ax.fill_between(
plot_t, low_winner, high_winner,
color=C[0], alpha=0.5,
label=f"{1 - ALPHA:.0%} interval"
);
ax.plot(
plot_t, (cum_winner[0] / plot_t[np.newaxis]).T,
c=C[0], alpha=0.75,
label="Bandit (samples)"
);
ax.plot(
plot_t, (cum_winner[1::25] / plot_t[np.newaxis]).T,
c=C[0], alpha=0.75
);
ax.hlines(
0.5, 1, N,
colors='k', linestyles='--'
);
ax.set_xlim(1, N);
ax.set_xlabel("Sessions");
ax.set_ylim(0, 1);
ax.yaxis.set_major_formatter(pct_formatter);
ax.set_yticks(np.linspace(0, 1, 5));
ax.set_ylabel("Traffic shown variant A");
ax.legend(loc=2)
ax.set_title(f"Cumulative bandit performance ({N_BANDIT} simulations)");
fig
Why Bayesian?¶
- Thompson sampling is intuitive and simple to implement
- Principled randomization
- Robustness against delayed feedback
- Marketers are natural Bayesians!
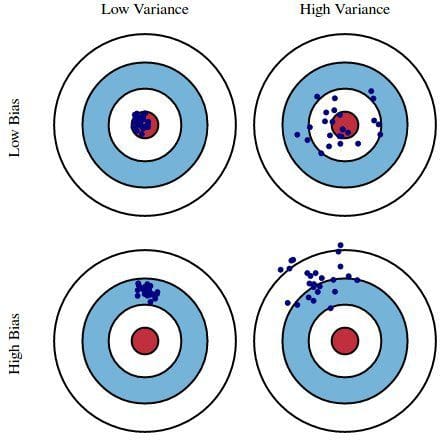
Bandit Bias¶
N = 1000
arms, rewards = simulate_bandits(
lambda: generate_rewards(A_RATE, B_RATE, N),
N, N_BANDIT
)
100%|██████████| 100/100 [00:13<00:00, 6.20it/s]
fig, (regret_ax, assign_ax) = plt.subplots(
ncols=2, sharex=True,
figsize=(2 * FIGURE_WIDTH, 6)
)
plot_t = np.arange(N) + 1
cum_rewards = rewards.cumsum(axis=1)
low_rewards, high_rewards = np.percentile(
cum_rewards, [100 * ALPHA / 2, 100 * (1 - ALPHA / 2)],
axis=0
)
regret_ax.fill_between(
plot_t, low_rewards, high_rewards,
color=C[0], alpha=0.5,
label=f"{1 - ALPHA:.0%} interval"
);
regret_ax.plot(
plot_t, cum_rewards.mean(axis=0),
c=C[0], label="Bandit (average)"
);
regret_ax.plot(
plot_t, A_RATE * plot_t,
c=C[1], ls='--',
label="Variant A"
);
regret_ax.plot(
plot_t, B_RATE * plot_t,
c=C[2], ls='--',
label="Variant B"
);
regret_ax.plot(
plot_t,
0.5 * (A_RATE + B_RATE) * plot_t,
c='k', ls='--',
label="A/B testing"
);
regret_ax.set_xlim(1, N);
regret_ax.set_xlabel("Sessions");
regret_ax.set_ylabel("Rewards");
regret_ax.legend(loc=2);
cum_winner = (arms == 1 * (A_RATE < B_RATE)).cumsum(axis=1)
low_winner, high_winner = np.percentile(
cum_winner / plot_t, [100 * ALPHA / 2, 100 * (1 - ALPHA / 2)],
axis=0
)
assign_ax.fill_between(
plot_t, low_winner, high_winner,
color=C[0], alpha=0.5,
label=f"{1 - ALPHA:.0%} interval"
);
assign_ax.plot(plot_t, cum_winner.mean(axis=0) / plot_t);
assign_ax.hlines(
0.5, 1, N,
colors='k', linestyles='--'
);
assign_ax.set_xlabel("Sessions");
assign_ax.set_ylim(0, 1);
assign_ax.yaxis.set_major_formatter(pct_formatter);
assign_ax.set_yticks(np.linspace(0, 1, 5));
assign_ax.set_ylabel("Traffic shown better variant");
fig.suptitle(f"Cumulative bandit performance ({N_BANDIT} simulations)");
fig
fig, ax = plt.subplots()
plot_t = np.arange(N) + 1
a_obs_rate = (rewards * (arms == 0)).cumsum(axis=1) \
/ np.maximum(1, (arms == 0).cumsum(axis=1))
b_obs_rate = (rewards * (arms == 1)).cumsum(axis=1) \
/ np.maximum(1, (arms == 1).cumsum(axis=1))
ax.plot(
plot_t, a_obs_rate.mean(axis=0),
c=C[0], label="Variant A (observed average)"
);
ax.plot(
plot_t, b_obs_rate.mean(axis=0),
c=C[1], label="Variant B (observed average)"
);
ax.hlines(
A_RATE, 1, N,
color=C[0], linestyles='--',
label="Variant A (actual)"
);
ax.hlines(
B_RATE, 1, N,
color=C[1], linestyles='--',
label="Variant B (actual)"
);
ax.set_xlim(1, N);
ax.set_xlabel("Sessions");
ax.set_ylim(
0.5 * min(A_RATE, B_RATE),
1.5 * max(A_RATE, B_RATE)
);
ax.yaxis.set_major_formatter(pct_formatter);
ax.set_ylabel("Reward rate");
ax.legend();
ax.set_title(f"Cumulative bandit performance ({N_BANDIT} simulations)");
fig
fig, ax = plt.subplots()
a_obs_rate = (rewards * (arms == 0)).cumsum(axis=1) \
/ np.maximum(1, (arms == 0).cumsum(axis=1))
b_obs_rate = (rewards * (arms == 1)).cumsum(axis=1) \
/ np.maximum(1, (arms == 1).cumsum(axis=1))
low, high = np.percentile(
a_obs_rate,
[100 * ALPHA / 2, 100 * (1 - ALPHA / 2)],
axis=0
)
ax.fill_between(
plot_t, low, high,
color=C[0], alpha=0.5
);
low, high = np.percentile(
a_obs_rate,
[100 * 2 * ALPHA / 2, 100 * (1 - 2 * ALPHA / 2)],
axis=0
)
ax.fill_between(
plot_t, low, high,
color=C[0], alpha=0.5
);
low, high = np.percentile(
a_obs_rate,
[100 * 4 * ALPHA / 2, 100 * (1 - 4 * ALPHA / 2)],
axis=0
)
ax.fill_between(
plot_t, low, high,
color=C[0], alpha=0.5
);
ax.plot(
plot_t, a_obs_rate.mean(axis=0),
c=C[0], label="Observed average"
);
ax.hlines(
A_RATE, 1, N,
linestyles='--',
label="Actual"
);
ax.set_xlim(1, N);
ax.set_xlabel("Sessions");
ax.set_ylim(0., 2. * A_RATE);
ax.yaxis.set_major_formatter(pct_formatter);
ax.set_ylabel("Variant A reward rate");
ax.legend(loc=1);
ax.set_title(f"Cumulative bandit performance ({N_BANDIT} simulations)");
fig

Inverse propensity weighting¶
$$ \hat{r}^{\textrm{IPS}}_A = \frac{1}{n} \sum_{t = 1}^n \frac{Y_i \cdot \mathbb{I}(A_t = 1)}{P(A_t = 1\ |\ \mathcal{D}_{1, t - 1})} $$where
$$ A_t = \begin{cases} 1 & \textrm{session } t \textrm{ saw variant A} \\ 0 & \textrm{session } t \textrm{ saw variant B} \end{cases}. $$For a more complete overview of inverse propensity weighting and related approaches to causal inference/data missing not at random, Improving efficiency and robustness of the doubly robust estimator for a population mean with incomplete data gives a good overview.
For simplicity in this talk, we only implement inverse propensity weighting. The general results are similar (with slightly less variance) for doubly robust estimation and related methods.
Calculating $P(A_t = 1\ |\ \mathcal{D}_{1, t - 1})$
ts_fig
a_post_alpha = (rewards * (arms == 0)).cumsum(axis=1) + 1
a_post_beta = ((1 - rewards) * (arms == 0)).cumsum(axis=1) + 1
b_post_alpha = (rewards * (arms == 1)).cumsum(axis=1) + 1
b_post_beta = ((1 - rewards) * (arms == 1)).cumsum(axis=1) + 1
%%time
N_MC = 500
a_samples = sp.stats.beta.rvs(
a_post_alpha[..., np.newaxis],
a_post_beta[..., np.newaxis],
size=(N_BANDIT, N, N_MC)
)
b_samples = sp.stats.beta.rvs(
b_post_alpha[..., np.newaxis],
b_post_beta[..., np.newaxis],
size=(N_BANDIT, N, N_MC)
)
a_prob = np.empty((N_BANDIT, N))
a_prob[:, 0] = 0.5
a_prob[:, 1:] = (a_samples > b_samples).mean(axis=2)[:, :-1]
CPU times: user 14.6 s, sys: 5.24 s, total: 19.8 s Wall time: 19.9 s
a_prob_ = (a_prob + 1e-12)
a_ips_est = 1. / plot_t * (rewards * (arms == 0) / a_prob_).cumsum(axis=1)
b_ips_est = 1. / plot_t * (rewards * (arms == 1) / (1 - a_prob_)).cumsum(axis=1)
fig, ax = plt.subplots()
plot_t = np.arange(N) + 1
a_obs_rate = (rewards * (arms == 0)).cumsum(axis=1) \
/ np.maximum(1, (arms == 0).cumsum(axis=1))
b_obs_rate = (rewards * (arms == 1)).cumsum(axis=1) \
/ np.maximum(1, (arms == 1).cumsum(axis=1))
ax.plot(
plot_t, a_obs_rate.mean(axis=0),
c=C[0], label="Variant A (observed average)"
);
ax.plot(
plot_t, b_obs_rate.mean(axis=0),
c=C[1], label="Variant B (observed average)"
);
ax.plot(
plot_t, a_ips_est.mean(axis=0),
c='k', label="IPS estimate"
);
ax.plot(
plot_t, b_ips_est.mean(axis=0),
c='k'
);
ax.hlines(
A_RATE, 1, N,
color=C[0], linestyles='--',
label="Variant A (actual)"
);
ax.hlines(
B_RATE, 1, N,
color=C[1], linestyles='--',
label="Variant B (actual)"
);
ax.set_xlim(1, N);
ax.set_xlabel("Sessions");
ax.set_ylim(
0.5 * min(A_RATE, B_RATE),
1.75 * max(A_RATE, B_RATE)
);
ax.yaxis.set_major_formatter(pct_formatter);
ax.set_ylabel("Reward rate");
ax.legend();
ax.set_title(f"Cumulative bandit performance ({N_BANDIT} simulations)");
fig
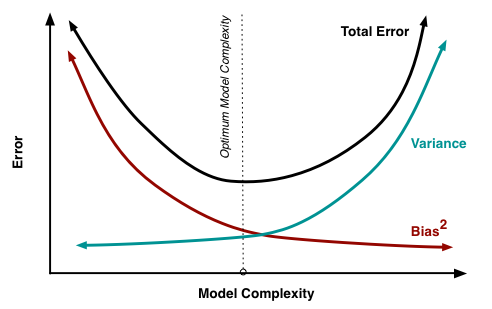
Bias-variance tradeoff¶
fig, (naive_ax, ips_ax) = plt.subplots(
ncols=2, sharex=True, sharey=True,
figsize=(2 * FIGURE_WIDTH, FIGURE_HEIGHT)
)
low, high = np.percentile(
a_obs_rate,
[100 * ALPHA / 2, 100 * (1 - ALPHA / 2)],
axis=0
)
naive_ax.fill_between(
plot_t, low, high,
color=C[0], alpha=0.5
);
naive_ax.plot(
plot_t, a_obs_rate.mean(axis=0),
c=C[0]
);
naive_ax.hlines(
A_RATE, 1, N,
color=C[0], linestyles='--'
);
naive_ax.set_xlim(1, N);
naive_ax.set_xlabel("Sessions");
naive_ax.set_ylim(0., 3 * A_RATE);
naive_ax.yaxis.set_major_formatter(pct_formatter);
naive_ax.set_ylabel("Reward rate");
naive_ax.set_title("Naive estimate");
low, high = np.percentile(
a_ips_est,
[100 * ALPHA / 2, 100 * (1 - ALPHA / 2)],
axis=0
)
ips_ax.fill_between(
plot_t, low, high,
color='k', alpha=0.5
);
ips_ax.plot(
plot_t, a_ips_est.mean(axis=0),
c='k'
);
ips_ax.hlines(
A_RATE, 1, N,
color=C[0], linestyles='--'
);
ips_ax.set_xlabel("Sessions");
ips_ax.set_title("IPS estimate");
fig.suptitle(f"Cumulative bandit performance ({N_BANDIT} simulations)");
fig
Intuition: the variant with the highest reward rate should receive the most traffic.
obs_opp_sign = np.sign(
(a_obs_rate - b_obs_rate) \
* ((arms == 0).cumsum(axis=1) - (arms == 1).cumsum(axis=1))
) == -1
ips_opp_sign = np.sign(
(a_ips_est - b_ips_est) \
* ((arms == 0).cumsum(axis=1) - (arms == 1).cumsum(axis=1))
) == -1
fig, ax = plt.subplots()
ax.plot(
plot_t, obs_opp_sign.mean(axis=0),
label="Naive estimate"
);
ax.plot(
plot_t, ips_opp_sign.mean(axis=0),
label="IPS estimate"
);
ax.set_xlim(1, N);
ax.set_xlabel("Sessions");
ax.yaxis.set_major_formatter(pct_formatter);
ax.set_ylabel("Probability intuition is wrong");
ax.legend(loc=1);
fig
Learn more¶

%%bash
jupyter nbconvert \
--to=slides \
--reveal-prefix=https://cdnjs.cloudflare.com/ajax/libs/reveal.js/3.2.0/ \
--output=city-tech-bayes-bandits \
./city-tech-bayes-bandits.ipynb
[NbConvertApp] Converting notebook ./city-tech-bayes-bandits.ipynb to slides [NbConvertApp] Writing 2698296 bytes to ./city-tech-bayes-bandits.slides.html


