ASE1302 - Midterm exam¶

$$ \newcommand{\eg}{{\it e.g.}} \newcommand{\ie}{{\it i.e.}} \newcommand{\argmin}{\operatornamewithlimits{argmin}} \newcommand{\mc}{\mathcal} \newcommand{\mb}{\mathbb} \newcommand{\mf}{\mathbf} \newcommand{\minimize}{{\text{minimize}}} \newcommand{\diag}{{\text{diag}}} \newcommand{\cond}{{\text{cond}}} \newcommand{\rank}{{\text{rank }}} \newcommand{\range}{{\mathcal{R}}} \newcommand{\null}{{\mathcal{N}}} \newcommand{\tr}{{\text{trace}}} \newcommand{\dom}{{\text{dom}}} \newcommand{\dist}{{\text{dist}}} \newcommand{\R}{\mathbf{R}} \newcommand{\Z}{\mathbf{Z}} \newcommand{\SM}{\mathbf{S}} \newcommand{\ball}{\mathcal{B}} \newcommand{\bmat}[1]{\begin{bmatrix}#1\end{bmatrix}} $$

Jong-Han Kim (jonghank@inha.ac.kr)

---

시험 시작 전, 다음의 ’학생 명예선서(Honor Code)’를 아래에 옮겨 적고 학번과 이름을 적어 서명하시오.

학생 명예선서:

• “나는 타인의 도움을 받지 않고 정직하게 시험에 응할 것을 서약합니다.”

• “By signing this pledge, I promise to adhere to exam requirements and maintain the highest level of ethical principles during the exam period.”

---

---

학생 명예선서:

• (한글/영문 중 하나를 옮겨 적으시오)

학번:

이름:

---

(Problem 1) 다음과 같이 수열 $a_n$, $b_n$, $t_n$, $p_n$을 ($n=0,1,2,\dots$) 사용하는 알고리듬을 통해, 원주율 $\pi$를 수치적으로 계산해 보려고 한다.

---

1. 수열의 초기치 $a_0$, $b_0$, $t_0$, $p_0$를 다음과 같이 정의한다.

$$ { a_{0}=1\qquad b_{0}={\frac {1}{\sqrt {2}}}\qquad t_{0}={\frac {1}{4}}\qquad p_{0}=1.} $$

2. 자연수 $n=1,2,\dots$에 대해 다음을 반복한다.

$$ { {\begin{aligned}a_{n+1}&={\frac {a_{n}+b_{n}}{2}},\\\\b_{n+1}&={\sqrt {a_{n}b_{n}}},\\\\t_{n+1}&=t_{n}-p_{n}\left(\frac{a_{n}-b_{n}}{2}\right)^{2},\\\\p_{n+1}&=2p_{n}.\\\end{aligned}}} $$

참고로, $a_{n+1}$과 $b_{n+1}$은 각각 직전 단계에서의 $a_n$과 $b_n$의 산술 평균과 기하 평균이므로, 반복을 거듭할 수록 $a_n$과 $b_n$은 서로 접근하게 된다.

3. $n$번째 반복 단계에서 $\pi$의 근사값인 $\pi_n$은 다음과 같이 계산할 수 있다. $\pi_n$과 $\pi_{n-1}$의 차이가 충분히 작으면 ($|\pi_n - \pi_{n-1}|< 10^{-15}$을 만족하면) 반복을 중단하고 알고리듬을 종료한다.

$${ \pi_{n} = {\frac {(a_{n}+b_{n})^{2}}{4t_{n}}}.}$$

---

(P1-a) 위의 알고리듬을 구현하여 소숫점 열 자리 이상의 정확도를 갖는 $\pi$의 근사값을 구하시오. 이 정도의 정확도는 몇 번의 반복 연산을 통해 얻어지는가? 다시 말해, 위의 알고리듬은 $n$이 얼마일 때 종료되는가?

(P1-b) 위의 결과에서서 $\pi_n$의 수렴 과정을 그래프를 통해 확인하시오. 마찬가지로 $a_n$과 $b_n$의 그래프를 통해 $a_n$과 $b_n$이 서로 가까워짐을 확인하시오.

---

(Problem 2) 어떤 인공위성이 우주발사체에 실려 발사되었고, 발사체 추진기관의 연소가 모두 종료된 후 위성이 분리되었다. 이 때, 위성은 적도 상공 고도 $h_0=800\,\text{km}$에 위치해 있었고, 속도는 정북 방향으로 $v_0=9\,\text{km/s}$로 수평에서 $\beta_0 = \frac{\pi}{18}\,\text{rad}(=10 \deg) $ 윗 방향을 향하고 있었다고 한다. 아래 그림의 녹색 화살표를 참고하시오.

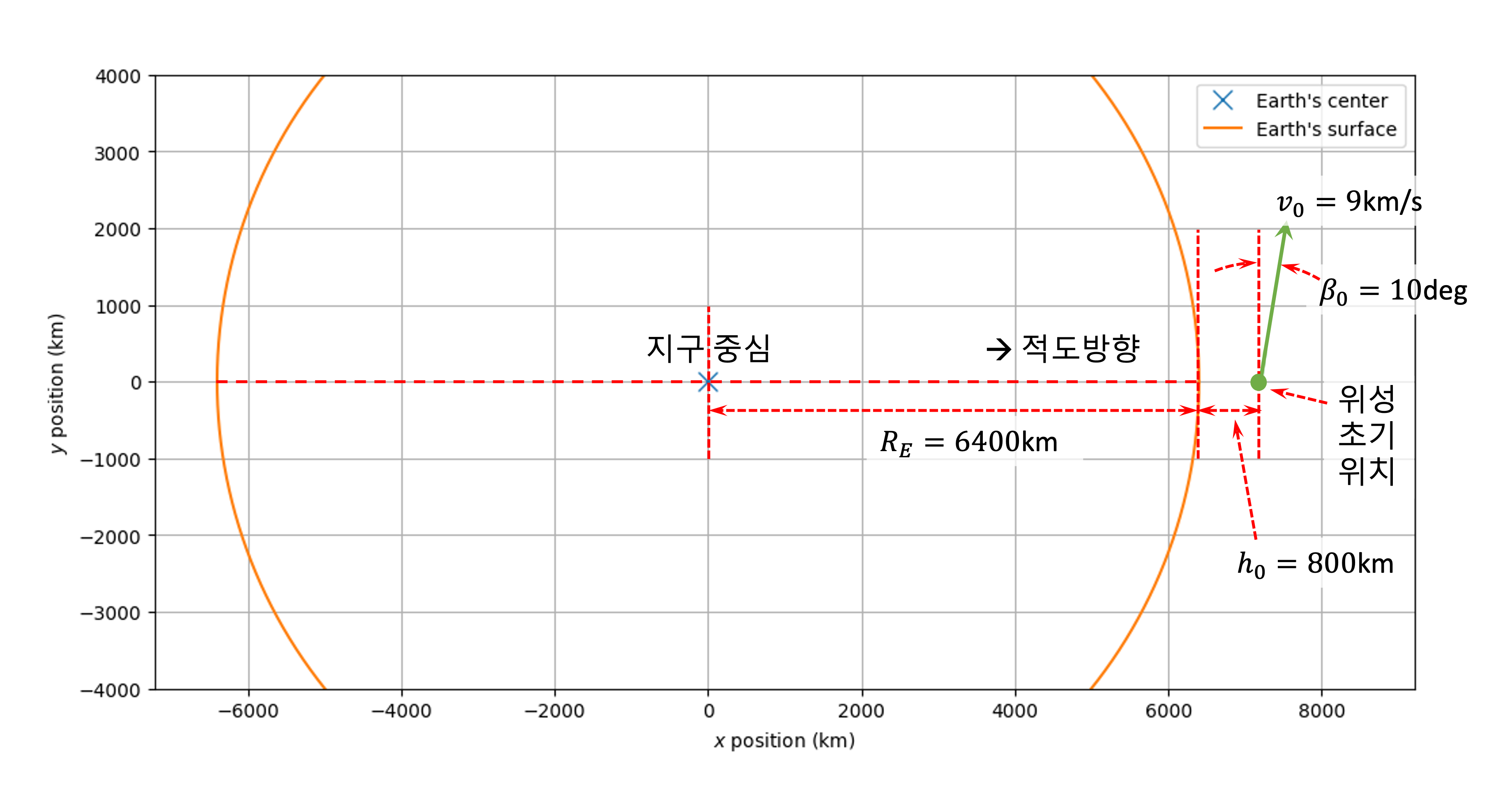
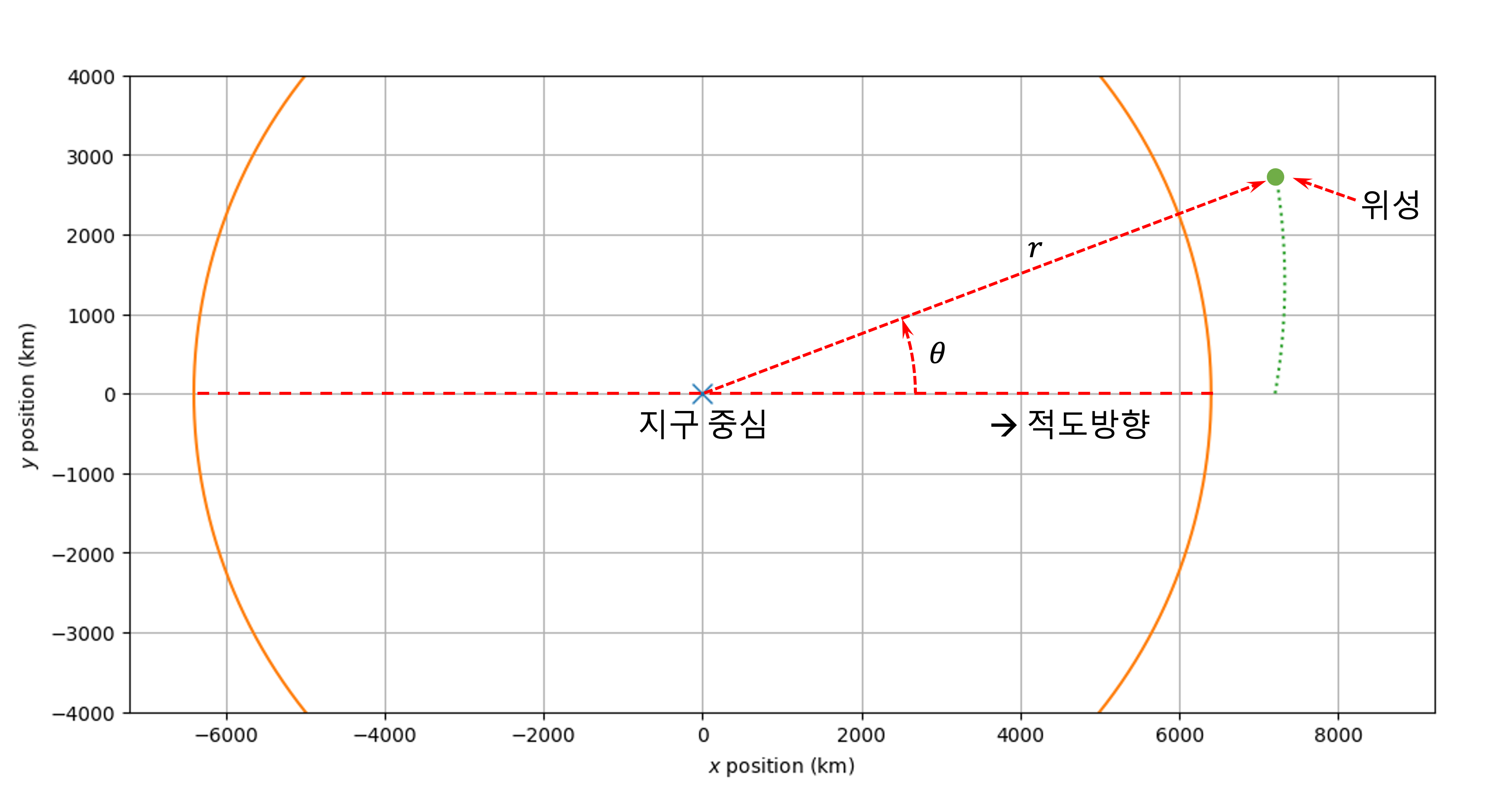
이 문제에서는 이 인공위성의 궤도를 그려보고 다양한 초기 속도 변화에 대한 궤도 형태를 분석하려고 한다. 인공위성의 운동이 위 그림의 $x-y$ 평면 상에서만 일어난다고 가정하면, 인공위성의 궤적은 변수 $r$과 $\theta$를 사용하여 다음과 같이 표현할 수 있다.

$$ r = \frac{p^2/\mu}{1+\epsilon \cos (\theta-C)}\\ $$

여기에서 $r$과 $\theta$는 인공위성의 위치를 표현하는 변수들로, $r$은 지구 중심으로부터의 거리, $\theta$는 적도 방향으로부터의 각 변위(위도)를 의미한다. $r$의 단위는 미터, $\theta$의 단위는 라디안이다. 그 외의 다른 변수들은 모두 고정된 상수로, 다음에 간략히 설명되어 있다.

• $\mu$는 중력상수와 지구질량의 곱으로, 다음과 같다.

$$ \mu = GM_E = 3.986\times 10^{14} m^3/s^2\\ $$

• $p$는 인공위성의 단위 질량당 각 운동량을 의미하며, 각운동량 보존 법칙에 의해 항상 일정하므로, 초기 조건으로부터 다음과 같이 계산될 수 있다. $r_0$는 분리 순간 (초기) 인공위성의 지구 중심으로부터 거리로, $r_0 = R_E + h_0$와 같다. 지구는 반경 $R_E$의 구로 가정하며, $R_E = 6400\,\text{km}$이다.

\begin{align*} p &= r_0 v_0 \cos \beta_0\\ r_0 &= R_E + h_0 \\ \end{align*}

• $\epsilon$은 인공위성 궤도의 이심율로, 초기 조건에 의해 다음과 같이 결정된다. 수식에 나타나는 $q$는 인공위성의 단위질량당 에너지로, 에너지 보존 법칙에 의해 항상 일정하므로 초기 조건으로부터 다음과 같이 계산할 수 있다.

\begin{align*} \epsilon &= \sqrt{1 + \frac{2p^2q}{\mu^2}}\\ q &= \frac{v_0^2}{2}- \frac{\mu}{r_0}\\ \end{align*}

• $C$는 초기 조건에 의해 결정되는 위상각으로, 위에서 $p$, $\mu$, $\epsilon$을 얻은 후 다음과 같이 계산할 수 있다. $\cos^{-1}(\cdot)$는 numpy 모듈의 arccos() 함수를 통해 계산할 수 있다.

$$ C = -\cos^{-1}\left( \frac{p^2}{ r_0\mu\epsilon} - \frac{1}{\epsilon} \right) $$

주의: 위의 모든 수식에서 거리의 단위는 m, 속도의 단위는 m/s, 각도의 단위는 rad을 사용해야 한다.

(P2-a) 단위 질량당 각 운동량 $p$, 이심율 $\epsilon$, 그리고 위상각 $C$를 계산하여 출력하시오.

(P2-b) 이 인공위성의 궤도를 그리시오 (힌트: $0\le\theta\le 2\pi$ 범위의 $\theta$에 대해 $r$을 계산한 후 $(x,y)=(r\cos\theta, r\sin\theta)$의 자취를 평면 상에 도시하여 얻을 수 있음). 지구를 반지름 6400km의 원으로 함께 표시하고, 이 인공위성의 궤도가 원형/타원형/포물선/쌍곡선 중 어뗘한 형태인지 확인하시오. 참고로 plt.axis('equal') 명령을 통해 그래프의 x축과 y축 스케일을 동일하게 도시할 수 있다.

(P2-c) 이 인공위성의 궤적에서, 인공위성이 지구와 가장 멀리 떨어졌을 때와 가장 가까울 때의 고도는 몇 km인가?

(P2-d) 2021년 10월의 누리호 발사과정에서, 3단 로켓의 연소가 조기 종료됨으로 인해 목표했던 연소 종료 속도 $v_0$가 얻어지지 못한 문제가 발생하였고, 이에 따라 더미 위성이 목표 궤도를 형성하지 못한채 지구로 추락할 것으로 예측되었다. 위에서 여러분이 만든 코드를 활용해서, 다양한 초기 속도 $v_0$에 대해 인공위성의 궤도가 어떻게 변화하는지 살펴 보고, 연소 종료 속도 $v_0$가 몇 km/s 이하일 때 위성이 지표면으로 추락할 것인지 계산해 보시오 (정확히 계산할 필요는 없으며, 유효숫자 두세자리 정도까지의 정확도로 답하시오). 목표 고도 $h_0$와 진입각 $\beta_0$는 예상대로 ($h_0=800\,\text{km}$, $\beta_0=10\,\text{deg}$)달성되었고, 목표 속도만이 미달되었다고 가정한다.