Rocket trajectories¶

$$ \newcommand{\eg}{{\it e.g.}} \newcommand{\ie}{{\it i.e.}} \newcommand{\argmin}{\operatornamewithlimits{argmin}} \newcommand{\mc}{\mathcal} \newcommand{\mb}{\mathbb} \newcommand{\mf}{\mathbf} \newcommand{\minimize}{{\text{minimize}}} \newcommand{\diag}{{\text{diag}}} \newcommand{\cond}{{\text{cond}}} \newcommand{\rank}{{\text{rank }}} \newcommand{\range}{{\mathcal{R}}} \newcommand{\null}{{\mathcal{N}}} \newcommand{\tr}{{\text{trace}}} \newcommand{\dom}{{\text{dom}}} \newcommand{\dist}{{\text{dist}}} \newcommand{\R}{\mathbf{R}} \newcommand{\SM}{\mathbf{S}} \newcommand{\ball}{\mathcal{B}} \newcommand{\bmat}[1]{\begin{bmatrix}#1\end{bmatrix}} \newcommand{\loss}{\ell} \newcommand{\eloss}{\mc{L}} \newcommand{\abs}[1]{| #1 |} \newcommand{\norm}[1]{\| #1 \|} \newcommand{\tp}{T} $$

ASE3001: Computational Experiments for Aerospace Engineering, Inha University.

Jong-Han Kim (jonghank@inha.ac.kr)

This example involves the kinematics of a projectile, whose dynamical relations can be described by the following differential equations

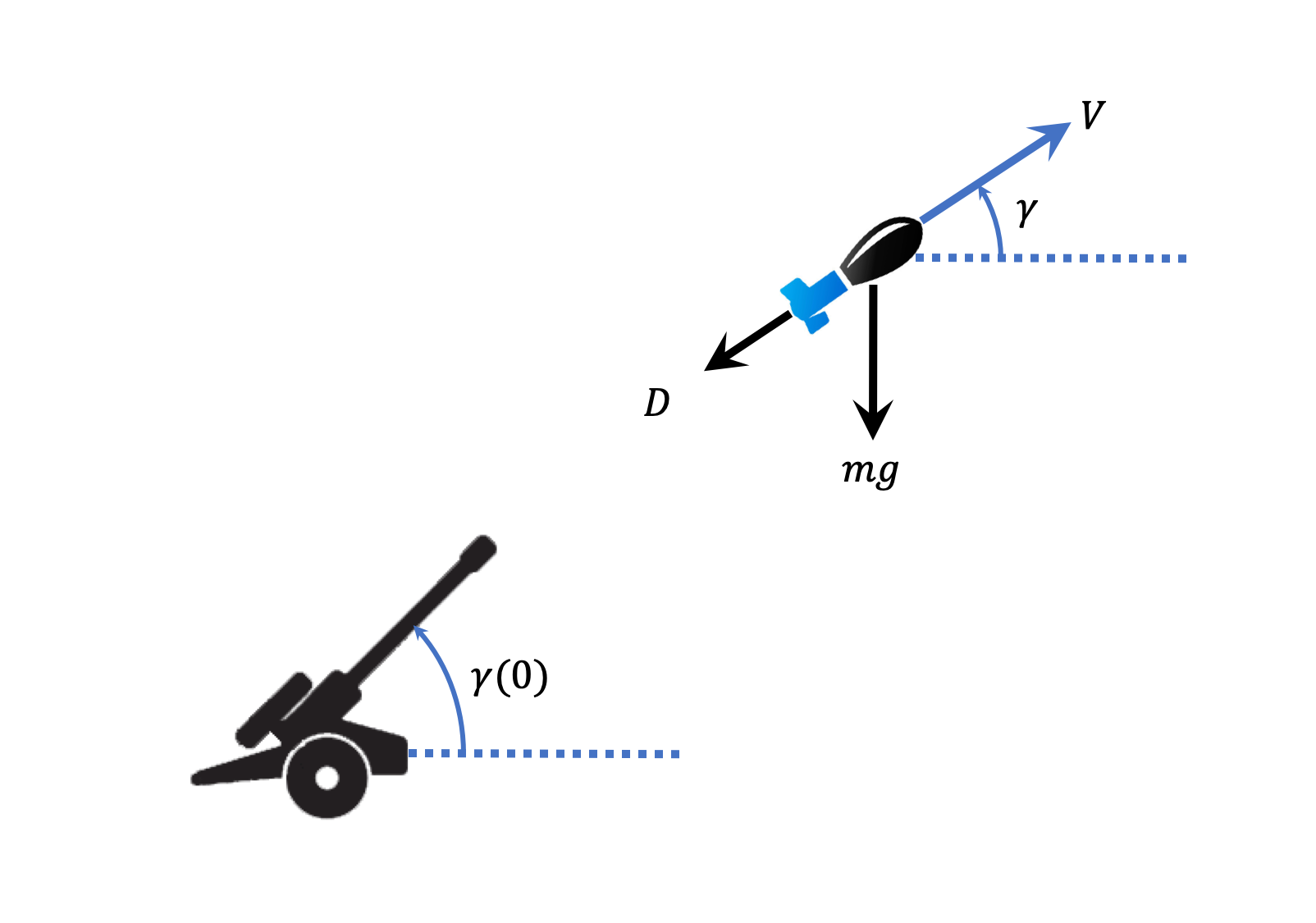
$$ \begin{aligned} m\dot{V} &= -0.5\rho V^2 S C_d - mg\sin\gamma \\ V\dot{\gamma} &= -g\cos\gamma \\ \dot{R} &= V\cos\gamma \\ \dot{h} &= V\sin\gamma \end{aligned} $$

where $V$, and $\gamma$ represents the speed and the flight path angle of the projectile, where a positive $\gamma$ implies the projectile is going up, and $\gamma=+\pi/2$ implies vertical ascend.

Throughout this problem, you can assume that the gravitational acceleration is constant, $g=9.8m/s^2$, and the air density is well approximated by the following formula.
$$ \rho(h) = 1.225 \left(1-2.256\times 10^{-5}h \right)^{5.256} $$

Suppose a projectile with the following specifications is launched.

$m$: mass (=$40kg$)
$d$: diameter (=$16cm$)
$S$: cross-section area (=$\pi d^2/4$)
$C_d$: drag coefficient (=$0.2$)
$V(0)$: initial velocity (=$1000m/s$)

(Problem 1) For various initial launch angles, $\gamma(0) = 20,25,\dots, 65, 70$ degrees, plot the vertical trajectory (on $R-h$ plane) and the time history of the projectile's speed.

In [ ]:

# your code here

(Problem 2) With which initial launch angle, $\gamma(0)$, should the projectile be launched, so that it reaches its maximum range? Answers upto the two most significant digits would suffice.

In [ ]:

# your code here

(Problem 3) Suppose you use the projectile for a parcel delivery service for your customers. Then you will probably need to make at least two modifications to your system, since the initial and the final speed of the projectile are too much high. So you decided to use a small engine, that will slowly accelerate the projectile in the beginning, and a small parachute that decelerates the projectile when it reaches the target. Your parachute deploys when $h\le 1000m$ and $\gamma\le 0$

So your model now looks like,

\begin{align*} m\dot{V} &= -0.5\rho V^2 S C_d - mg\sin\gamma + T \\ V\dot{\gamma} &= -g\cos\gamma \\ \dot{R} &= V\cos\gamma \\ \dot{h} &= V\sin\gamma \end{align*}

with

$$ T = \begin{cases} 4000N & \text{if } t \le 5 s\\ 0 & \text{otherwise} \end{cases} $$

and $$ C_{d}= \begin{cases} 10 & \text{if } \gamma\le 0 \text{ and } h\le 1000m \\ 0.2 & \text{otherwise} \end{cases} $$

Find a sample trajectory when

$m$: mass (=$40kg$)
$d$: diameter (=$16cm$)
$S$: cross-section area (=$\pi d^2/4$)
$V(0)$: initial velocity (=$10$)
$\gamma(0)$: launch angle (=$50\text{deg}$)

In [ ]:

# your code here

(Problem 4) What is the appropriate launch angle, $\gamma(0)$, for delivery to a customer located at 12km far? How long would the delivery to this customer take? How high would your rocket reach during the flight?

In [ ]:

# your code here

Initial launch angle: 44.1(deg)
Landing at: 11.98608871680277(km)
Delivery time: 54.2(sec)
Maximum altitude: 2.101809671615191(km)