ASE1302 - Assignment #06¶

$$ \newcommand{\eg}{{\it e.g.}} \newcommand{\ie}{{\it i.e.}} \newcommand{\argmin}{\operatornamewithlimits{argmin}} \newcommand{\mc}{\mathcal} \newcommand{\mb}{\mathbb} \newcommand{\mf}{\mathbf} \newcommand{\minimize}{{\text{minimize}}} \newcommand{\diag}{{\text{diag}}} \newcommand{\cond}{{\text{cond}}} \newcommand{\rank}{{\text{rank }}} \newcommand{\range}{{\mathcal{R}}} \newcommand{\null}{{\mathcal{N}}} \newcommand{\tr}{{\text{trace}}} \newcommand{\dom}{{\text{dom}}} \newcommand{\dist}{{\text{dist}}} \newcommand{\R}{\mathbf{R}} \newcommand{\Z}{\mathbf{Z}} \newcommand{\SM}{\mathbf{S}} \newcommand{\ball}{\mathcal{B}} \newcommand{\bmat}[1]{\begin{bmatrix}#1\end{bmatrix}} $$

Jong-Han Kim (jonghank@inha.ac.kr)

Ho-Young Jeon (hy13776@inha.edu)

---

6.1 n이라는 이름의 매개변수를 입력으로 받아서 이 값의 제곱 값을 반환하는 square(n) 함수를 정의하고 이 함수를 호출하여 3과 4의 제곱을 출력하고자 한다. 밑줄 친 부분에 들어갈 알맞은 코드를 채우고 전체 코드를 실행하시오.

---

6.2 m과 n이라는 이름의 매개변수를 두 개 입력받아서 이 두 값 중에서 큰 값을 반환하는 max2(m, n) 함수와 작은 값을 반환하는 min2(m, n)함수를 구현하시오. 100과 200을 인자로 넣어서 호출하여 그 결과를 확인하시오. 이를 위하여 밑줄 친 부분에 들어갈 알맞은 코드를 채우고 전체 코드를 실행하시오.

---

6.3 n1, n2, n3라는 이름의 매개변수를 3개 입력받아서 이 값 중에서 가장 큰 값을 반환하는 max3(n1, n2, n3)함수와 가장 작은 값을 반환하는 min3(n1, n2, n3) 함수를 구현하시오. 사용자로부터 임의의 정수 3개를 입력으로 받아서 이 함수를 호출하여 다음과 같은 출력을 내 보이도록 하여라.

---

6.4 섭씨온도(celsius)를 화씨온도(fahrenheit)로 변환하는 식은 다음과 같다. 이 식을 바탕으로 섭씨온도를 0도에서 50도까지 10도 단위로 증가시키면서 이에 해당하는 화씨온도를 출력하는 프로그램을 작성하시오. 이를 위하여 섭씨온도를 인자로 받아서 화씨온도를 반환하는 cel2fah() 함수를 만들도록 하여라.

fahrenheit = (9/5)*celsius +32

---

6.5 임의의 수를 입력으로 받은 다음 이 수가 소수인지 아닌지를 판단하는 함수 is_prime(n)을 작성하여라. 만일 n이 소수이면 True, 그렇지 않으면 False를 반환하도록 하여라(힌트 : 소수는 1과 자기자신 이외에는 약수를 가지지 않는다. 따라서 어떤 수 n을 2에서 부터 n-1까지의 수로 나누어 보면 된다. 만일 중간에 n을 나눌 수 있는 수가 있다면 이 수는 소수가 아닐것이다.)

---

6.6 n!은 n(n-1)(n-2) $\cdots$2 $\cdot$1의 식으로 표현되는 값이다. 양의 정수 n을 매개변수로 받아서 팩토리얼 값을 반환하는 factorial(n) 함수를 구현하여라. 이 함수를 재귀 함수를 사용하지 말고 for문을 사용하여 작성하여라. 이 함수를 이용하여 factorial(5), factorial(7), factorial(10)의 값을 출력하는 출력문을 구현하여라.

---

6.7 사용자로 부터 $x_1, y_1, x_2, y_2$의 값을 받아들인 다음 $(x_1, y_1)$ 좌표에서 $(x_2, y_2)$ 좌표를 잇는 직선의 거리를 출력하고자 한다. distance($x_1, y_1, x_2, y_2$)를 구현하고 이 함수를 호출하여 다음과 같이 화면에 직선과 거리를 출력하도록 하여라.

---

6.8 Bisection method

이분탐색은 근이 반드시 존재하는 폐구간 $[x_l, x_u]$을 이분한 후, 이 중 근이 존재하는 하위 폐구간을 선택하는 것을 반복하여서 근을 찾는 알고리즘이다.기본적인 방법은 $[x_l, x_u]$에서 연속인 함수 f에 대하여 $f(x_l)f(x_u)<0$ 인 폐구간 $[x_l, x_u]$에 대해서 계속해서 $\frac{x_u+x_l}{2}$을 하여 나오는 또 다른 수를 하나의 폐구간 끝점으로 잡은 새로운 폐구간을 만든다. 이와 같은 방법으로 계속 n번을 시행하게 되면 점점 함수 f(x)=0를 만족하는 x에 다가가게 된다. 이때, 허용 오차를 $\epsilon$, n번째 구간을 $[a_n, b_n]$이라고 할때, 다음 조건이 만족될때까지 반복한다.

$$ \left| a_n - b_n \right| < \epsilon $$

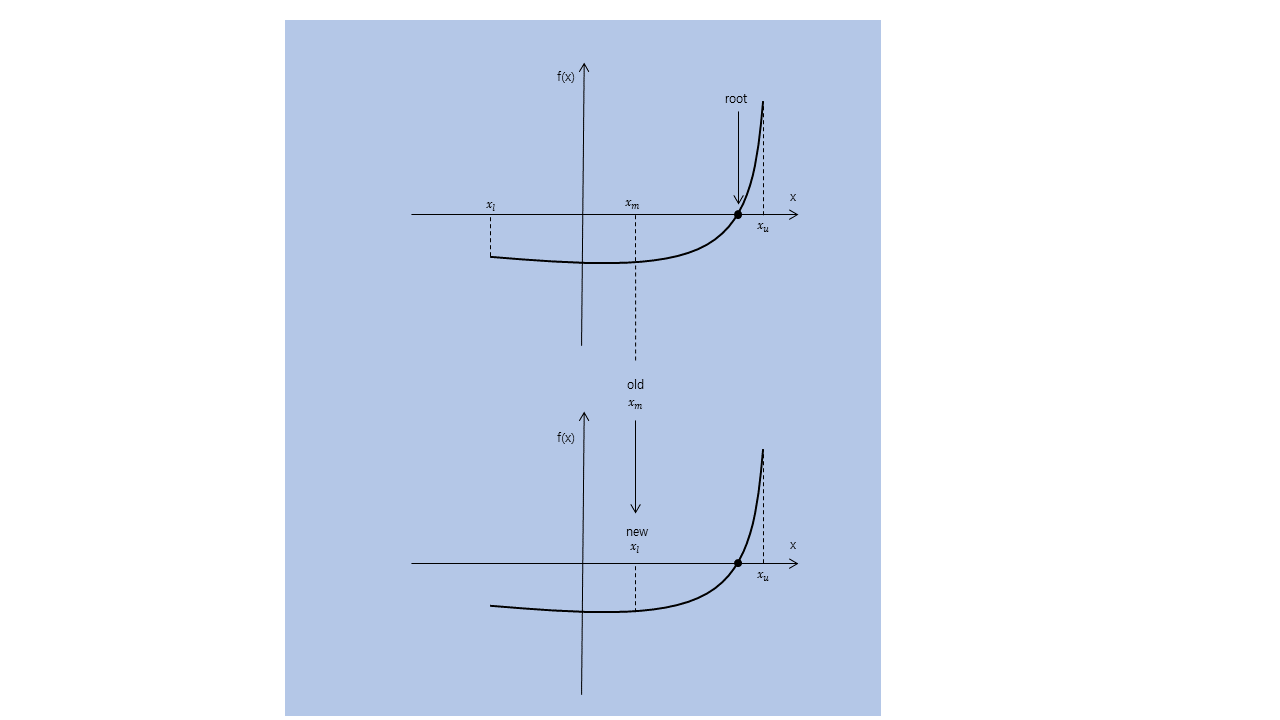
구간 $[x_l, \ x_u] = [0 ,\ 4]$ 에서 이분법을 사용하여 다음 함수의 근을 구하라. 이때, bisection_search 함수를 이용하여 다음 표와 값이 일치하는지 확인한다. 이때, 허용오차 $\epsilon = 0.01$로 가정한다. $$ f(x) = x^2 - 2\\ $$

i	$x_l$	f($x_l$)	$x_m$	f($x_m$)	$x_u$	f($x_u$)	$\epsilon$
0	0	-2	2	2	4	14	4
1	0	-2	1	-1	2	2	2
2	1	-1	1.5	0.25	2	2	1
3	1	-1	1.25	-0.4375	1.5	0.25	0.5000
4	1.25	-0.4375	1.375	-0.1094	1.5	0.25	0.2500
5	1.375	-0.1094	1.4375	0.0664	1.5	0.25	0.1250
6	1.375	-0.1094	1.40625	-0.0225	1.4375	0.0664	0.0625
7	1.4062	-0.0225	1.4219	0.0217	1.4375	0.0664	0.0313
8	1.4062	-0.0225	1.414	-0.004	1.4219	0.0217	0.0156
9	1.414	-0.004			1.4219	0.0217	0.0078