0. PyTorch¶
우리는 PyTorch라는 딥러닝 프레임워크를 사용할 것이므로 실습하기에 앞서 torch를 임포트합니다.
Colab에서는 PyTorch가 이미 설치되어 있으므로 별도 설치가 필요하지 않습니다.
import torch
1. 스칼라(Scalar)¶
스칼라(Scalar)는 하나의 상수를 의미합니다. PyTorch에서 스칼라를 만드는 방법은 간단합니다.
- torch.tensor([숫자])
var1 = torch.tensor([1])
type(var1)
torch.Tensor
var1
tensor([1])
타입은 torch.Tensor가 나옵니다. torch.Tensor는 파이토치에서 제공하는 파이썬의 자료형이라고 보시면됩니다.
이번에는 또 다른 스칼라를 만들어봤습니다.
var2 = torch.tensor([5.8])
var2
tensor([5.8000])
이번에는 두 개의 스칼라를 가지고 곱셈이나 나눗셈 연산을 해보겠습니다.
파이썬에서는 덧셈은 +, 뺄셈은 -, 곱셈은 * 나눗셈은 / 을 의미합니다.
# 두 스칼라의 덧셈 연산
var1 + var2
tensor([6.8000])
# 두 스칼라의 뺄셈 연산
var1 - var2
tensor([-4.8000])
# 두 스칼라의 곱셈 연산
var1 * var2
tensor([5.8000])
# 두 스칼라의 나눗셈 연산
var1 / var2
tensor([0.1724])
파이토치는 두 스칼라의 연산을 위해서 덧셈, 뺄셈, 곱셈, 나눗셈 등의 다양한 파이토치만의 연산 함수들을 제공합니다.
위에서 수행했던 사칙연산들을 이번에는 파이토치 함수를 통해서 값을 구해봅시다.
- add, sub, mul, div
# torch 함수를 사용
torch.add(var1, var2) # 덧셈
tensor([6.8000])
torch.sub(var1, var2) # 뺄셈
tensor([-4.8000])
torch.mul(var1, var2) # 곱셈
tensor([5.8000])
torch.div(var1, var2) # 나눗셈
tensor([0.1724])
2. 벡터(Vector)¶
스칼라(Scalar)가 하나의 상수를 표현한다면, 벡터(Vector)는 상수가 두 개 이상 나열되었을 때를 벡터라고 합니다.
PyTorch에서는 벡터(Vector)를 다음과 같이 표현합니다.
- torch.tensor([숫자1, 숫자2, 숫자3, ... , 숫자9999])
vector1 = torch.tensor([1, 2, 3]) # 상수가 두개 이상이면 백터라고 함.
vector1
tensor([1, 2, 3])
type(vector1)
torch.Tensor
여기서 수학적인 용어 한 가지만 짚고갈게요. 우리는 벡터를 차원이라는 용어로 부를 때가 있습니다.
가령, 'N차원 벡터'라고 부른다면 여기서 N은 벡터 안에 숫자가 몇 개있는지를 의미합니다.
vector1은 숫자가 지금 안에 3개가 있기 때문에 우리는 vector1은 '3차원 벡터'라고 부를 수 있습니다.
2-1. 벡터의 사칙 연산¶
이번에는 또 다른 벡터를 만들어서 벡터의 연산을 벡터의 다양한 연산을 한 번 해보겠습니다.
vector2 = torch.tensor([10, 20, 30])
vector2
tensor([10, 20, 30])
순서대로 덧셈, 뺄셈, 곱셈, 나눗셈을 수행해봅시다.
# 덧셈
vector1 + vector2
tensor([11, 22, 33])
# 뺄셈
vector1 - vector2
tensor([ -9, -18, -27])
# 곱셈
vector1 * vector2
tensor([10, 40, 90])
# 나눗셈
vector1 / vector2
tensor([0.1000, 0.1000, 0.1000])
물론 파이토치가 제공하는 연산 함수를 통해서도 가능합니다.
- add, sub, mul, div
# 덧셈
torch.add(vector1, vector2)
tensor([11, 22, 33])
# 뺄셈
torch.sub(vector1, vector2)
tensor([ -9, -18, -27])
# 곱셈
torch.mul(vector1, vector2)
tensor([10, 40, 90])
# 나눗셈
torch.div(vector1, vector2)
tensor([0.1000, 0.1000, 0.1000])
2-2. 벡터의 내적(중요)¶
벡터의 내적 연산(dot product)도 torch.dot()을 통해서 가능합니다.
두 벡터의 내적이라고 함은 x = [a1, a2, a3], y=[b1, b2, b3] 다음의 두 벡터가 있다면,
a1 x b1 + a2 x b2 + a3 x b3를 우리는 벡터의 내적이라고 합니다.
여기서 내적은 다음과 같이 이루어졌습니다.
- 1 x 10 + 2 x 20 + 3 x 30 = 140
print(vector1)
print(vector2)
tensor([1, 2, 3]) tensor([10, 20, 30])
# 내적
torch.dot(vector1, vector2)
tensor(140)
1*10+2*20+3*30
140
3. 행렬(Matrix)¶
행렬(Matrix)는 2개 이상의 벡터 값을 가지고 만들어진 값으로 행과 열의 개념을 가진 숫자의 나열입니다.
matrix1 = torch.tensor([[1, 2], [3, 4]]) # 백터 2개로 행렬 만들었다.
print(matrix1)
tensor([[1, 2],
[3, 4]])
위 행렬은 2행, 2열을 가지는 행렬입니다. 또는 2 x 2 행렬이라고도 부릅니다.
또 다른 행렬을 하나 더 만들어봅시다.
matrix2 = torch.tensor([[7, 8], [9, 10]])
print(matrix2)
tensor([[ 7, 8],
[ 9, 10]])
3-1. 행렬의 사칙연산¶
이제 두 행렬 간 사칙 연산을 수행해봅시다.
matrix1 + matrix2
tensor([[ 8, 10],
[12, 14]])
matrix1 - matrix2
tensor([[-6, -6],
[-6, -6]])
# 동일한 위치에 있는 원소들끼리 곱합니다.
matrix1 * matrix2
tensor([[ 7, 16],
[27, 40]])
matrix1 / matrix2 # 동일한 위치에 있는 원소들끼리 곱합니다.
tensor([[0.1429, 0.2500],
[0.3333, 0.4000]])
스칼라와 벡터일 때와 마찬가지로 파이토치에서 제공하는 연산 함수를 통해서 사칙 연산을 수행할 수도 있습니다.
# 행렬의 덧셈
torch.add(matrix1, matrix2)
tensor([[ 8, 10],
[12, 14]])
# 행렬의 뺄셈
torch.sub(matrix1, matrix2)
tensor([[-6, -6],
[-6, -6]])
# 행렬의 원소별 곱셈
torch.mul(matrix1, matrix2)
tensor([[ 7, 16],
[27, 40]])
# 행렬의 나눗셈
torch.div(matrix1, matrix2)
tensor([[0.1429, 0.2500],
[0.3333, 0.4000]])
3-2. 행렬의 곱셈¶
행렬의 곱셈에 대한 참고 자료 : https://mathbang.net/562
행렬의 곱셈에 대한 참고 자료 : https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=alwaysneoi&logNo=100194421088
벡터에 내적이라는 개념이 있었던 것처럼 행렬에도 행렬의 곱셈이라는 특수한 연산이 존재합니다.
- torch.matmul()
torch.matmul(matrix1, matrix2)
tensor([[25, 28],
[57, 64]])
4. 텐서(Tensor)¶
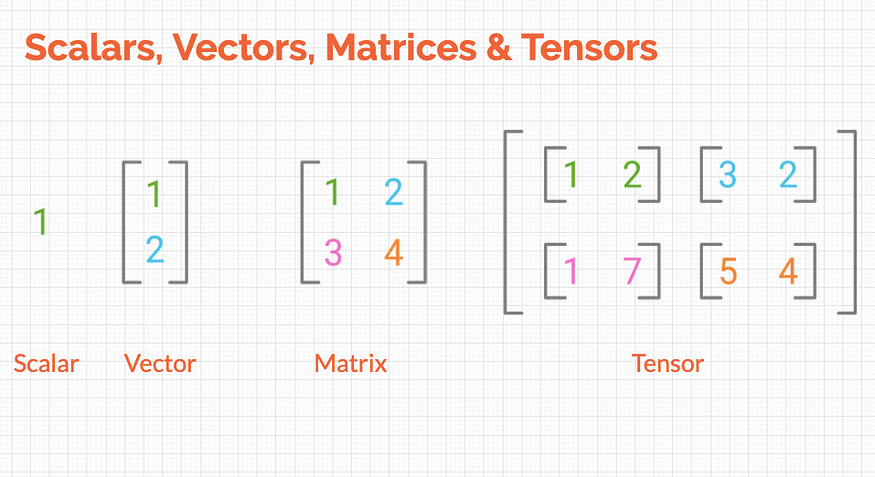
스칼라는 하나의 숫자를 의미했습니다.
벡터는 다수의 스칼라가 모인 개념입니다.
행렬은 다수의 벡터가 모인 개념입니다.
텐서는 다수의 행렬이 모이면 이때부터는 일반적으로 텐서(Tensor)라고 부릅니다.
from IPython.display import Image
Image(url='https://miro.medium.com/max/875/1*jRyyMAhS_NZxqyv3EoLCvg.png')
다음과 같이 두 개의 텐서를 만들었습니다.
tensor1 = torch.tensor([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
print(tensor1)
tensor([[[1, 2],
[3, 4]],
[[5, 6],
[7, 8]]])
tensor2 = torch.tensor([[[9, 10], [11, 12]], [[13, 14], [15, 16]]])
print(tensor2)
tensor([[[ 9, 10],
[11, 12]],
[[13, 14],
[15, 16]]])
4-1. 텐서의 사칙연산¶
이번에는 텐서의 사칙 연산을 한 번 수행해봅시다.
# 텐서의 덧셈
tensor1 + tensor2
tensor([[[10, 12],
[14, 16]],
[[18, 20],
[22, 24]]])
# 텐서의 뺄셈
tensor1 - tensor2
tensor([[[-8, -8],
[-8, -8]],
[[-8, -8],
[-8, -8]]])
# 텐서의 곱셈
tensor1 * tensor2
tensor([[[ 9, 20],
[ 33, 48]],
[[ 65, 84],
[105, 128]]])
# 텐서의 나눗셈
tensor1 / tensor2
tensor([[[0.1111, 0.2000],
[0.2727, 0.3333]],
[[0.3846, 0.4286],
[0.4667, 0.5000]]])
파이토치에서 제공하는 연산 함수를 통해서 사칙 연산을 수행할 수도 있습니다.
# 텐서의 덧셈
torch.add(tensor1, tensor2)
tensor([[[10, 12],
[14, 16]],
[[18, 20],
[22, 24]]])
# 텐서의 뺄셈
torch.sub(tensor1, tensor2)
tensor([[[-8, -8],
[-8, -8]],
[[-8, -8],
[-8, -8]]])
# 텐서의 원소별 곱셈
torch.mul(tensor1, tensor2)
tensor([[[ 9, 20],
[ 33, 48]],
[[ 65, 84],
[105, 128]]])
# 텐서의 나눗셈
torch.div(tensor1, tensor2)
tensor([[[0.1111, 0.2000],
[0.2727, 0.3333]],
[[0.3846, 0.4286],
[0.4667, 0.5000]]])
4-2. 텐서의 곱셈¶
벡터의 내적, 행렬의 곱셈과 마찬가지로 우리는 텐서의 곱셈 또한 가능합니다.
기본적으로 원리는 행렬의 곱셈입니다.
torch.matmul(tensor1, tensor2)
tensor([[[ 31, 34],
[ 71, 78]],
[[155, 166],
[211, 226]]])