TCLab Heat Transfer Introduction¶
*Introduction to the Temperature Control Lab:* The Temperature Control Lab is used in the Course Problem Solving with Programming for Engineers. In addition to this introduction, the hands-on lab module includes three parts:
- TCLab A: Build Loops, Plots, and Regressions
- TCLab B: Interpolate and Solve Equations
- TCLab C: Determine Thermal Conductivity

See https://apmonitor.com/heat.htm for additional Python setup and example programs.
*Learning Objective:* Students will be able to make order of magnitude estimates, assess reasonableness of solutions, and select appropriate levels of solution sophistication.
Background on Heat Transfer¶
There are several modes of heat transfer including radiative, convective, and conductive. Radiative heat transfer is from the motion of particles and emitted as electromagnetic photons primarily as infrared radiation. Convective heat transfer is with the surrounding fluid such as air. Convection can be forced such as from a blower or natural such as in quiescent conditions. Conductive heat transfer is through solid contact as the energy transfers away but, unlike convection, the contact material is stationary. For each situation, determine which form best describes the heat transfer.
- Hair is dried with a blow dryer
- A pan is heated on a gas stove
- Food is cooked in the hot pan
- Sunlight warms the ground
TCLab Activity¶
The temperature of transitor increases as electrical current flows through the small device. Energy is dispersed away from the transitor with two primary mechanisms: convection and radiation. The amount of heat lost by convection $\left(q_{conv}\right)$ is proportional to the temperature difference between the transistor $\left(T_x\right)$ and the surrounding air temperature $\left(T_{air}\right)$.
$q_{conv} = h \, A \, \left(T_{air}-T_x\right)$
A finned heat sink is attached to the transistor to increase the surface area and increase the heat removal. A temperature sensor is attached to the transistor to monitor the temperature.
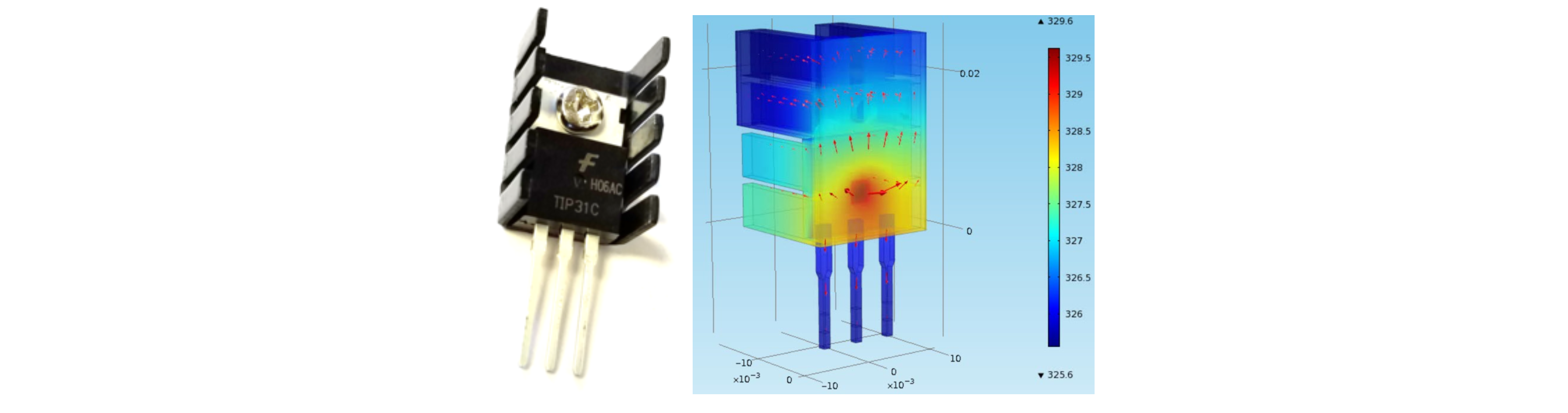
The surface area $(A)$ of the transistor and heat sink is about 12 $cm^2$. A convective heat transfer coefficient $(h)$ for quiescent air is approximately 10 $\frac{W}{m^2\,K}$. At lower temperatures, the heat generated by the transistor transfers away from the device primarily by convection but radiative heat transfer $\left(q_{rad}\right)$ may also be a contributing factor. The surrounding temperature $\left(T_\infty\right)$ is that of objects such as walls or the ceiling. In this case is the same as the air temperature.
$q_{rad} = \epsilon \, \sigma \, A \, \left(T_\infty^4-T_x^4\right)$
Some of the constants needed for the transistor and finned heat sink are shown in the table below. Some of the constants in the table are not needed for this calculation.
| *Quantity* | *Value* |
|---|---|
| Heat capacity ($C_p$) | 500 $\frac{J}{kg\,K}$ |
| Air Temperature ($T_{air}$) | 20 $^oC$ |
| Surrounding Temperature ($T_\infty$) | 20 $^oC$ |
| Surface Area ($A$) | 1.2e-3 $m^2$ (12 $cm^2$) |
| Mass ($m$) | 0.004 $kg$ (4 $gm$) |
| Heat Transfer Coefficient ($h$) | 10 $\frac{W}{m^2\,K}$ |
| Emissivity ($\epsilon$) | 0.9 |
| Stefan Boltzmann Constant ($\sigma$) | 5.67e-8 $\frac{W}{m^2-K^4}$ |
*Action:* Calculate the amount of heat lost by convection and by radiation at temperatures between 20 $^oC$ and 200 $^oC$. Create a plot that shows the heat transfer by each by filling in the convection and radiation expressions.
# Energy Balance
convection = h*A*(Ta-Tx)
radiation = eps*sigma*A*(Tinf**4-Tx**4)
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
Ta = 20 + 273.15 # Ambient air temperature (K)
Tinf = Ta # Surrounding temperature (K)
h = 10.0 # Heat Transfer Coefficient (W/m^2-K)
m = 4.0/1000.0 # Mass (kg)
Cp = 0.5 * 1000.0 # Heat capacity (J/kg-K)
A = 12.0 / 100.0**2 # Surface Area (m^2)
eps = 0.9 # Emissivity
sigma = 5.67e-8 # Stefan-Boltzman
T = np.linspace(20,200) # Temperature (degC)
Tx = T + 273.15 # Temperature (K)
# Energy Balance
convection = # fill-in
radiation = # fill-in
#Plotting
plt.figure(figsize=(10,5))
plt.plot(T,-convection,'b-',label='Convection')
plt.plot(T,-radiation,'r--',label='Thermal Radiation')
plt.xlabel('Temperature $^oC$')
plt.ylabel('Heat Loss (W)')
plt.legend()
File "<ipython-input-1-b816dbc1f5ec>", line 18 convection = # fill-in ^ SyntaxError: invalid syntax
*Action:* What is the relative importance of heat transfer by convection and radiation at low (<80 $^oC$) and high (>180 $^oC$) temperature. Which heat transfer mode increases relatively more as the temperature increases?
*Action:* Use the plot above and make a function that prints values of the graph to determine the temperature where radiative heat transfer is greater than the heat lost by convective heat transfer.
print(np.transpose([-convection, -radiation, T])) # The graphing above must be run first
# Use values printed below to see when radiation heat loss becomes greater than convection heat loss
Equation for convection heat loss: $q_{conv} = h \, A \, \left(T_{air}-T_x\right)$
Equation for radiation heat loss: $q_{rad} = \epsilon \, \sigma \, A \, \left(T_\infty^4-T_x^4\right)$
*Action:* Which of these factors could increase only thermal radiation?
*Action:* Which of these factors could increase both thermal radiation and convection?
*Action:* Without the finned heat sink, the transistor surface area is smaller. Show the effect on thermal radiation and convection with changing the surface area from 12 $cm^2$ to 2 $cm^2$. (Use the graph program and change the value for surface area)
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
Ta = 20 + 273.15 # Ambient air temperature (K)
Tinf = Ta # Surrounding temperature (K)
h = 10.0 # Heat Transfer Coefficient (W/m^2-K)
m = 4.0/1000.0 # Mass (kg)
Cp = 0.5 * 1000.0 # Heat capacity (J/kg-K)
A = ('Change this value') # Surface Area (m^2)
eps = 0.9 # Emissivity
sigma = 5.67e-8 # Stefan-Boltzman
T = np.linspace(20,200) # Temperature (degC)
Tx = T + 273.15 # Temperature (K)
# Energy Balance
convection2 = h*A*(Ta-Tx)
radiation2 = eps*sigma*A*(Tinf**4-Tx**4)
#Plotting
plt.figure(figsize=(10,5))
plt.plot(T,-convection,'b-',label='Convection')
plt.plot(T,-radiation,'r--',label='Thermal Radiation')
plt.plot(T,-convection2,'b-',label='Convection',lw=3) #New variable
plt.plot(T,-radiation2,'r--',label='Thermal Radiation',lw=3) #New variable
plt.xlabel('Temperature $^oC$')
plt.ylabel('Heat Loss (W)')
plt.legend()
*Action:* If the transistor needs to dissipate 1 Watt of power from radiation and convection, what temperature will the transistor be with a surface area of 2 $cm^2$ versus 12 $cm^2$? (Combine then plot values or use the similiar function from above)
plt.figure(figsize=(10,5))
plt.plot(T,-convection,'b-',label='Convection')
plt.plot(T,-radiation,'r--',label='Thermal Radiation')
# Try different colors and line types, e.g. k or *
plt.plot(T,-(convection+radiation),'g:',label='Thermal Radiation')
plt.xlabel('Temperature $^oC$')
plt.ylabel('Heat Loss (W)')
plt.legend()
print(np.transpose([-(convection+radiation), T])) #Combined values in columns