Introdução¶
Esse algoritmo em geral supera boa parte dos outros algoritmos de aprendizagem de máquina (como já foi provado em inúmeros artigos científicos sobre o tema). Seu uso é ideal quando a tarefa a ser realizada é complexa, tal como reconhecimento de caracteres, de voz e de imagens. Além disso, O SVM foi considerado por vários anos como o mais eficiente na realização de classificações, mas devido ao aprimoramento de técnicas de deep learning (ou aprendizado profundo) usado em construções de redes neurais, o SVM perdeu seu título.
Como o SVM funciona?¶
Em geral, o objetivo do algoritmo é aprender a criar hiperplanos com margem máxima entre as classes (quanto maior a margem, melhor é a capacidade de predição do algoritmo). Além disso, dependendo da base de dados utilizada, pode ser construída apenas uma reta. O algoritmo tentará encontrar o melhor hiperplano ou reta possível que separe perfeitamente as classes com margem máxima. Para que isso aconteça, é feita diversas tentativas com a intenção de encontrar a melhor separação possível.

Como o algoritmo exige muitos cálculos a serem feitos, alguns dados começam a ser usados como vetores de suporte. Geralmente esses dados especiais são localizados em posições estratégicas, levando em consideração seu posicionamento em relação a margem e a reta utilizada. Dessa forma, a cada novo dado que for inserido para a realização da predição de sua classe, os cálculos serão bem menores devido a esses pontos de referência criados para auxilixar na construção de hiperplanos e retas.
Definição Formal¶
"Uma máquina de vetores de suporte (SVM, do inglês: support vector machine) é um conceito na ciência da computação para um conjunto de métodos de aprendizado supervisionado que analisam os dados e reconhecem padrões, usado para classificação e análise de regressão. O SVM padrão toma como entrada um conjunto de dados e prediz, para cada entrada dada, qual de duas possíveis classes a entrada faz parte, o que faz do SVM um classificador linear binário não probabilístico. Dados um conjunto de exemplos de treinamento, cada um marcado como pertencente a uma de duas categorias, um algoritmo de treinamento do SVM constrói um modelo que atribui novos exemplos a uma categoria ou outra. Um modelo SVM é uma representação de exemplos como pontos no espaço, mapeados de maneira que os exemplos de cada categoria sejam divididos por um espaço claro que seja tão amplo quanto possível. Os novos exemplos são então mapeados no mesmo espaço e preditos como pertencentes a uma categoria baseados em qual o lado do espaço eles são colocados."
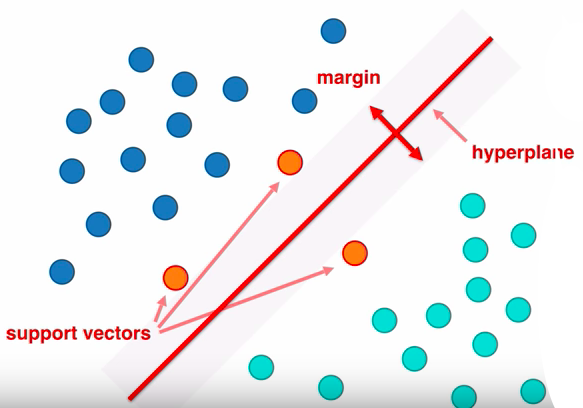
Observando as afirmações acima, é possível entender que o objetivo do SVM é encontrar uma linha de separação, mais comumente chamada de hiperplano entre dados distintos de classes. Essa linha busca a maximização das distâncias entre os pontos mais próximos em relação a cada uma das classes (geralmente utilizando vetores de suporte).
A distância entre o hiperplano e o primeiro ponto de cada classe é denominada de margem máxima. A ordem definida para realizar esses processos é a seguinte: primeiramente é feita a classificação das classes, definindo o máximo de pontos possíveis pertencentes a cada uma delas. Em seguida, é feita a maximização da margem. Ou seja, ela primeiro classifica as classes de forma correta e depois, em função dessa restrição, define a distância entre as margens.
Definindo a margem máxima¶
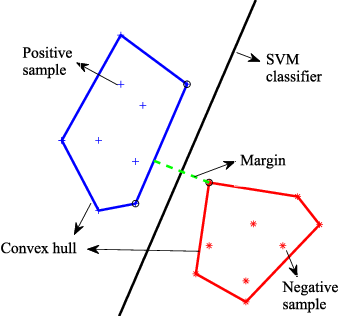
Para definir a margem máxima, é usada uma técnica chamada Convex Hulls (traduzindo literalmente seria envoltória ou casca convexa). Essa técnica tem o objetivo de traçar a distância entre determinados registros de modo a criar um envoltório entre os dados de uma determinada classe e, a partir da distância de cada um dos envoltórios da classe, é definido a margem máxima onde a reta se localizará.
SVMs não lineares¶
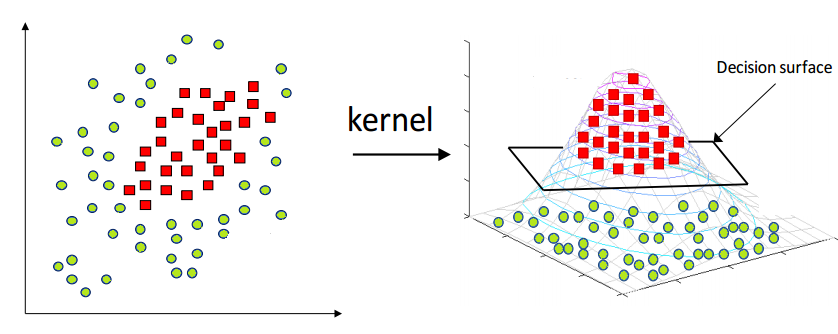
Quando os dados estão distribuidos de uma forma que não é possível fazer a separação entre classes, é utilizando uma técnica chamada kernel trick, esse que possui a finalidade de reagrupar os dados de modo com que eles fiquem com uma distribuição que garanta a separação entre as classes. E essa separação consiste em levar os dados para a terceira dimensão (aqui fica claro a ideia de hiperplano), caso seja necessário, usando transformações lineares.


Vantagens do SVM¶
Abaixo é possível conferir uma série de vantagens ao se utilizar o algoritmo de classificação Máquinas de Vetores de Suporte:
- Não é muito influenciado por ruídos;
- Utilizado para classificação e regressão;
- Aprende conceitos não presentes nos dados originais (principalmente quando realiza transformações lineares para aumentar a quantidade de atributos a serem analisados, esses não presentes na base original);
- Mais fácil de usar do que redes neurais;
Desvantagens do SVM¶
Abaixo é possível conferir uma série de desvantagens ao se utilizar o algoritmo de classificação Máquinas de Vetores de Suporte:
- Testar várias combinações de parâmetros;
- É um algoritmo lento;
- Black box (só é possível visualizar os resultados, não é possível visualizar nada sobre o modelo criado em relação a base de dados utilizada);