Aprendizaje Profundo¶

Diplomado en Inteligencia Artificial y Aprendizaje Profundo¶

Funciones de pérdida¶

Visualización funciones de pérdida modelos neuronales VGG56 y resnet56. Fuente: University of Maryland

Profesores¶

1. Alvaro Montenegro, PhD, ammontenegrod@unal.edu.co
2. Camilo José Torres Jiménez, Msc, cjtorresj@unal.edu.co
3. Daniel Montenegro, Msc, dextronomo@gmail.com

Asesora Medios y Marketing digital¶

4. Maria del Pilar Montenegro, pmontenegro88@gmail.com
5. Jessica López Mejía, jelopezme@unal.edu.co
6. Venus Puertas, vpuertasg@unal.edu.co

Jefe Jurídica¶

7. Paula Andrea Guzmán, guzmancruz.paula@gmail.com

Coordinador Jurídico¶

8. David Fuentes, fuentesd065@gmail.com

Desarrolladores Principales¶

9. Dairo Moreno, damoralesj@unal.edu.co
10. Joan Castro, jocastroc@unal.edu.co
11. Bryan Riveros, briveros@unal.edu.co
12. Rosmer Vargas, rovargasc@unal.edu.co

Expertos en Bases de Datos¶

13. Giovvani Barrera, udgiovanni@gmail.com
14. Camilo Chitivo, cchitivo@unal.edu.co

Introducción¶

Basado en Ravindra Parmar en towardsdatascience, Vishal Yathish en towardsdatascience

Las máquinas aprenden por medio de una función de pérdida. Es un método para evaluar qué tan bien un algoritmo específico modela los datos dados. Si las predicciones se desvían demasiado de los resultados reales, la función de pérdida arrojaría un número muy grande.

Un método de optimización es utilizado para encontrar los pesos y sesgos de una red neuronal que minimizan una función de pérdida. En esta lección, analizaremos varias funciones de pérdida y utilizadas en el dominio del aprendizaje de redes neuronales.

No existe una función de pérdida única para todos los algoritmos de entrenamiento de redes neuronales. En términos generales, las funciones de pérdida se pueden clasificar en dos categorías principales según el tipo de tarea de aprendizaje con la que nos enfrentemos: pérdidas de regresión y pérdidas de clasificación

• En la clasificación, estamos tratando de predecir la salida de un conjunto de valores categóricos finitos, por ejemplo, dado un gran conjunto de datos de imágenes de dígitos escritos a mano (MNIST), clasificándolos en uno de los dígitos 0–9.
• La regresión, por otro lado, se ocupa de predecir un valor continuo, por ejemplo, dado el área de una casa, el número de habitaciones, el tamaño de las habitaciones, predecir el precio de la habitación.

La imagen muestra los elementos necesarios para construir una función de pérdida:

• La entrada a la red $X$.
• La salida de la red $\hat{Y} = net(X)$
• La etiqueta $Y$.

Usamos la siguiente notación:

• $X =(X_1, X_2, X_3)$;
• $\hat{Y}=(\hat{Y}_1, \hat{Y}_2)$;
• $Y=(Y_1, Y_2)$.

$$ \large X \hspace{9cm} \hat{Y} = net(X) \hspace{4cm} Y $$

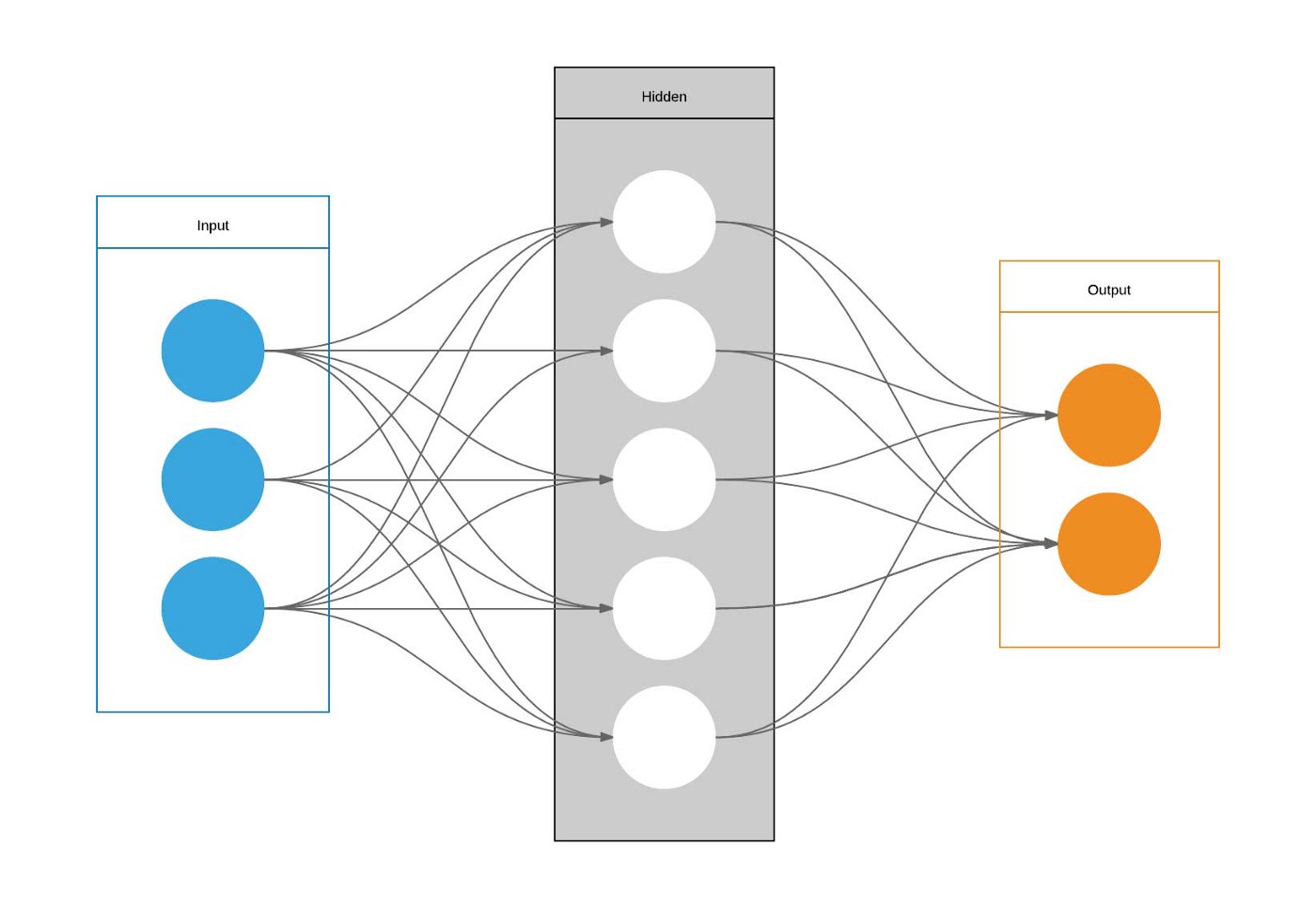
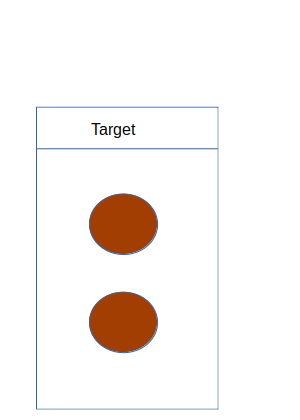
Basada en una imagen de Wiki-commons.

Una función de pérdida mide que tan cerca esta la salida de la red con respecto a la respectiva etiqueta.

Si por ejemplo, en el problema la salida y la etiqueta son tensores de forma (2,) y la función de pérdida es el error cuadrático medio, se tiene que

$$ \mathfrak{L} = \left[(\hat{y}_1 - y_1)^2 + (\hat{y}_2 - y_2)^2 \right] $$

Funciones de pérdida para regresión¶

En los problemas de regresión se supone que tanto la salida como la etiqueta con tensores de tipo float. En este caso algunas de las funciones de pérdida más utilizadas son:

Error cuadrático medio (ECM): Mean squared error (MSE)¶

En este caso, si se tiene $N$ datos para en un bloque de datos de entrenamiento, digamos $(x_i, y_i)$, en donde las $y_i$ son números, entonces la función de pérdida es

$$ \text{ECM} = \frac{1}{N} \sum_{i=1}^N (y_i-\hat{y}_i)^2 $$

Si la salida y la etiqueta son vectores, digamos de tamaño $J$, cada componente de los vectores escribe $\hat{y}_{ij}$ y ${y}_{ij}$ respectivamente. En este caso la función ECM toma la forma

$$ \text{ECM} = \frac{1}{N} \sum_{i=1}^N \sum_{j=1}^J (y_{ij}-\hat{y}_{ij})^2 $$

La desventaja de esta función de pérdida es que es muy sensible a valores extremos. Un valor extremo puede hacer crecer mucha la función de pérdida debido al cuadrado en la fórmula. Una opción para resolver esta situación es la siguiente función de pérdida.

Error absoluto medio (EAM): Mean absolute Value (MAE) ¶

En este caso, en lugar de calcular las diferencias al cuadrado de entre los $\hat{y}_i$ y los $y_i$ se toman las diferencias absolutas, es decir

$$ \text{EAM} = \frac{1}{N} \sum_{i=1}^N |y_i-\hat{y}_i| $$

o,

$$ \text{EAM} = \frac{1}{N} \sum_{i=1}^N \sum_{j=1}^J|y_{ij}-\hat{y}_{ij}| $$

La función de pérdida EAM no resuelve del todo los problemas, debido a que, si su valor es cercano a cero, los valores absolutos son cercanos a cero y esto impacta el cálculo del gradiente, debido a que la función valor absoluto no es derivable en cero. Una alternativa viable a estas dos funciones de pérdida es la siguiente.

Función de perdida de Hubber: Hubber loss¶

Para el caso de salida y etiqueta de forma (1,) la función de pérdida de Hubber se define como:

$$ \begin{align} \text{Hubber loss} &= \tfrac{1}{n}\sum_{i=1}^n (Y_i- \hat{Y}_i)^2 \hspace{2cm} |\hat{Y}_i-Y_i|\le \delta\\ &= \tfrac{1}{n}\sum_{i=1}^n |Y_i- \hat{Y}_i)| \hspace{2cm} |\hat{Y}_i-Y_i|> \delta \end{align} $$

y en el caso de tensores de salida y etiqueta de forma $(J,)$

$$ \begin{align} \text{Hubber loss} &= \tfrac{1}{N}\sum_{i=1}^N \sum_{j=1}^J(Y_{ij}- \hat{Y}_{ij})^2 \hspace{2cm} \sum_{j=1}^J|\hat{Y}_{ij}-Y_{ij}|\le \delta\\ &= \tfrac{1}{N}\sum_{i=1}^N \sum_{j=1}^J |Y_{ij}- \hat{Y}_{ij})| \hspace{2cm} \sum_{j=1}^J|\hat{Y}_{ij}-Y_{ij}|> \delta \end{align} $$

Si la diferencia absoluta entre el valor real y el predicho es menor o igual que un valor de umbral, $\delta$, entonces se aplica ECM. De lo contrario, si el error es suficientemente grande, se aplica EAM.

Funciones de pérdida para clasificación¶

En los problemas de clasificación, las etiquetas son discretas. Cada ejemplo de entrenamiento tiene una categoría asociada.

Funciones sigmoide y softmax¶

En los problemas de clasificación, lo usual es que las salida de la red sea un tensor de tipo float de forma $(1,)$ si se tienen dos clases y en general un tensor de tipo float de de forma $(J,)$ si se tiene $J$ clases. Este tensor se conoce como un tensor de pre-probabilidad.

En el caso binario (dos clases), es usual transformar la salida de la red con la función de activación sigmoide, la cual es la función de distribución acumulada estándar de la distribución logística. El sigmoide puede usarse en este caso con la activación en la capa de salida de la red. Esta función de activación es definida por

$$ \sigma(x) = \frac{e^x}{1 + e^x} = \frac{1}{1 + e^{-x}} = \frac{1}{2} + \frac{1}{2} \tanh\left(\frac{x}{2}\right). $$

La función softmax está diseñada para convertir un tensor de tipo float de forma $(J,)$ en un tensor de la misma forma que representa una distribución de probabilidad. Si $(Y_1, \ldots,Y_j, \ldots, Y_J)$ es un tensor de números reales, entonces $\text{softmax(Y)}$ es un tensor $p=(p_1, \ldots, p_j, \ldots, p_J)$, en donde

$$ p_j = \frac{e^{y_j}}{\sum_{k=1}^J e^{y_k}}. $$

Como podemos observar, la función softmax es una generalización natural del sigmoide cuando se tiene más de dos categorías.

En la práctica $p_j$ se interpreta como la probabilidad que la entrada $X$ pertenezca a la clase $j$.

Entropía cruzada binaria: Binary cross entropy¶

Esta función de pérdida es la más utilizada en los casos de clasificación en dos clases. En este caso se espera que la salida de la red neuronal y la etiqueta sean tensores de forma $(1,)$.

Puede revisar el origen de la entropía cruzada en el capítulo introductorio de teoría de la información. Técnicamente, la entropía cruzada para una entrada $X$ con salida $\hat{Y}$ y etiqueta $Y$ se define en este caso de la siguiente manera. En este caso las etiquetas solamente serán 0 o 1. Tenemos que $\hat{Y}= net(X)$, $\hat{p} = \sigma(\hat{Y})$, y

$$ \mathfrak{L} = -\left[(\log (\hat{p}) Y) + \log (1-\hat{p})(1-Y) \right]. $$

Entropía cruzada: Cross entropy¶

Para el caso de $J$ clases, definimos el tensor $Z = (Z_1, \ldots, Z_j, \ldots Z_J)$, en donde

$$ Z_j = \begin{cases} &1, \quad \text{si } Y=j\\ & 0, \quad \text{en otro caso} \end{cases} $$

Es decir, $Z$ es el vector que representa la codificación one-hot de la etiqueta $Y$. Observe que $Z$ solamente tiene 1 en la posición $j$, si la categoría de la etiqueta es $j$, y cero en el resto de posiciones.

Finalmente, para este caso la entropía cruzada es definida para el caso general de $N$ muestras en un lote de datos como

$$ \mathfrak{L} = -\frac{1}{N} \sum_{i=1}^N\left[ \sum_{j=1}^J Z_{ij}log (\hat{p}_{ij}) \right], $$

en donde $\hat{Y}_i= (\hat{Y}_{i1}, \ldots, \hat{Y}_{iJ})$ es la salida del la red para la entrada $X_i$, $\hat{p}_i = \text{softmax}(Y_i)$, y $Z_i$ la codificación one-hot de la etiqueta $Y_i$.

Funciones de Pérdida en Keras¶

Para revisar la descripción y forma de uso de las funciones de pérdida en Keras vaya aquí.

Perdidas para clasificación¶

• tf.keras.losses.BinaryCrossentropy: entropía cruzada binaria
• tf.keras.losses.CategoricalCrossentropy: entropía cruzada. Las etiquetas se espera en formato one-hot.
• SparseCategoricalCrossentropy: entropía cruzada dispersa. Las etiquetas esperadas son enteros
• tf.keras.losses.Poisson: pérdida = $\hat{Y} - Y \log (\hat{Y})$.
• tf.keras.losses.KLDivergence: divergencia Kullback-Leiber. $loss = Y * log(Y / \hat{Y})$.

Perdidas para regresión¶

• tf.keras.losses.MeanSquaredError: error cuadrático medio
• tf.keras.losses.MeanAbsoluteError: error aboluto medio
• tf.keras.losses.MeanAbsolutePercentageError: procentaje de error absoluto entre $Y$ y $\hat{y}$.
• tf.keras.losses.MeanSquaredLogarithmicError: $loss = (log(Y + 1.) - log(\hat{Y} + 1.))^2$
• tf.keras.losses.CosineSimilarity: similaridad coseno entre $Y$ y $\hat{y}$.
• tf.keras.losses.Huber: pérdida de Hubber
• tf.keras.losses.LogCosh: $logcosh = log((exp(x) + exp(-x))/2)$, en donde $x$ es el error $\hat{Y}-Y$.

Perdidas de tipo bisagra para clasificación¶

• tf.keras.losses.Hinge: $loss = maximum(1 - Y * \hat{Y}, 0)$
• tf.keras.losses.SquaredHinge: $loss = (maximum(1 - Y * \hat{Y}, 0))^2$
• tf.keras.losses.CategoricalHinge: $loss = maximum(neg - pos + 1, 0)$ en donde $neg=maximum((1-Y)*\hat{Y})$ y $pos=sum(Y*\hat{Y})$

Funciones de Pérdida en Pytorch¶

El detalle de las funciones de pérdida en Pytorch revise aquí.

• nn.L1Loss: Error absoluto medio.
• nn.nn.MSELoss: Error cuadrático medio.
• nn.BCELoss: pérdida entropía cruzada binaria.
• nn.CrossEntropyLoss: pérdida entropía cruzada. Puede incluir pesos para las clases.
• nn.NLLLoss: Perdida Log-verosimilitud negativa. Puede incluir pesos para las clases.
• nn.CTCLoss:Pérdida para Clasificación Temporal Conexionista. Para series de tiempo.
• nn.PoissonNLLLoss: Pérdida negativa de log verosimilitud con distribución de Poisson del objetivo.
• nn.GaussianNLLLoss: Pérdida log-verosimiltud negativa.
• nn.KLDivLoss: divergencia Kullback-Leibler.
• nn.BCEWithLogitsLoss: combina sigmoide con entropía binaria cruzada binaria.
• nn.HingeEmbeddingLoss: pérdida entre el tensor de entrada y las etiquetas marcadas como -1 o 1.
• nn.MultiLabelMarginLoss: Crea un criterio que optimiza una pérdida de multiclasificación en multiclase tipo bisagra (hinge).
• nn.HingeEmbeddingLoss: pérdida de incrustación de tipo bisagra.
• nn.HuberLoss: Crea un criterio que usa un término cuadrático si el error absoluto del elemento cae por debajo del delta y un término L1 con escala delta en caso contrario.
• nn.SmoothL1Loss: Crea un criterio que usa un término cuadrático si el error absoluto del elemento cae por debajo de beta y un término L1 en caso contrario.
• nn.nn.SoftMarginLoss:Crea un criterio que optimiza una clasificación de dos clases.
• nn.MultiLabelSoftMarginLoss: Crea un criterio que optimiza una pérdida uno contra todos de varias etiquetas en función de la entropía máxima, entre la entrada $X$ y la etiqueta $Y$ de tamaño (N, C).
• nn.CosineEmbeddingLoss: Usa un criterio basado en la similaridad coseno.
• nn.MultiMarginLoss:Crea un criterio que optimiza una pérdida de tipo hinge de clasificación multiclase
• nn.MultiMarginLoss: Crea un criterio que mide la pérdida de una tripleta de datos, dados los tensores de entrada $X_1$,$X_2$, $X_3$ y un margen con un valor mayor que 0.
• nn.TripletMarginWithDistanceLoss: Crea un criterio que mide la pérdida de una tripleta de dados los tensores de entrada $a$, $p$ y $n$ (que representan ejemplos de ancla, positivo y negativo, respectivamente), y una función de valor real no negativa ("función de distancia") utilizada para calcular la relación entre el ancla y ejemplo positivo (“distancia positiva”) y el ancla y ejemplo negativo (“distancia negativa”).