Aprendizaje Profundo¶

Diplomado en Ciencia de Datos¶

Introducción a convoluciones¶

Fuente: Cecbur, CC BY-SA 4.0, via Wikimedia Commons

Profesores¶

• Alvaro Montenegro, PhD, ammontenegrod@unal.edu.co
• Campo Elías Pardo, PhD, cepardot@unal.edu.co
• Daniel Montenegro, Msc, dextronomo@gmail.com
• Camilo José Torres Jiménez, Msc, cjtorresj@unal.edu.co

Estudiantes auxiliares¶

• Jessica López, jelopezme@unal.edu.co
• Camilo Chitivo, cchitivo@unal.edu.co
• Daniel Rojas, anrojasor@unal.edu.co

Asesora Medios y Marketing digital¶

• Maria del Pilar Montenegro, pmontenegro88@gmail.com
• Jessica López Mejía, jelopezme@unal.edu.co

Jefe Jurídica¶

• Paula Andrea Guzmán, guzmancruz.paula@gmail.com

Coordinador Jurídico¶

• David Fuentes, fuentesd065@gmail.com

Desarrolladores Principales¶

• Dairo Moreno, damoralesj@unal.edu.co
• Joan Castro, jocastroc@unal.edu.co
• Bryan Riveros, briveros@unal.edu.co
• Rosmer Vargas, rovargasc@unal.edu.co
• Venus Puertas, vpuertasg@unal.edu.co

Expertos en Bases de Datos¶

• Giovvani Barrera, udgiovanni@gmail.com
• Camilo Chitivo, cchitivo@unal.edu.co

Referencias¶

1. Ian Goodfellow, Yosua Bengio and Aaron Courville, Deep Learning, MIT press, 2016.
2. Vincent Doumolin and Francesco Vision, A guide to convolution arithmetic for deep learning, ArXiv:1603.07285v2, 2018
3. Applied Deep Learning - Part 4: Convolutional Neural Networks
4. Gentle Dive into Math Behind Convolutional Neural Networks
5. [Deep Learning for Computer Vision

Stanford - Spring 2022](https://cs231n.github.io/convolutional-networks/)

1. Alvaro Montenegro y Daniel Montenegro, Inteligencia Artificial y Aprendizaje Profundo, 2022
2. Alvaro Montenegro, Daniel Montenegro Campo Elías Pardo, y Oleg Jarma, Inteligencia Artificial y Aprendizaje Profundo Avanzado, 2022
3. Alvaro Montenegro, Daniel Montenegro, Campo Elías Pardo y Oleg Jarma, Ciencia de datos, 2022

Contenido¶

• Introducción
• ¿Qué es una Convolución?
  • Uso en Procesamiento de Imágenes
  • Ejemplos Reales
• Relleno (Padding)
• Filtros
• Múltiples filtros
• Reducción en el número de parámetros
• Agrupamiento (Pooling)
• Convoluciones 1D y 3D
• Representación matricial de las convoluciones

Introducción ¶

Las redes neuronales convolucionales (RNC) son un tipo especializado de red neuronal para procesar datos que tiene una topología conocida similar a una cuadrícula.

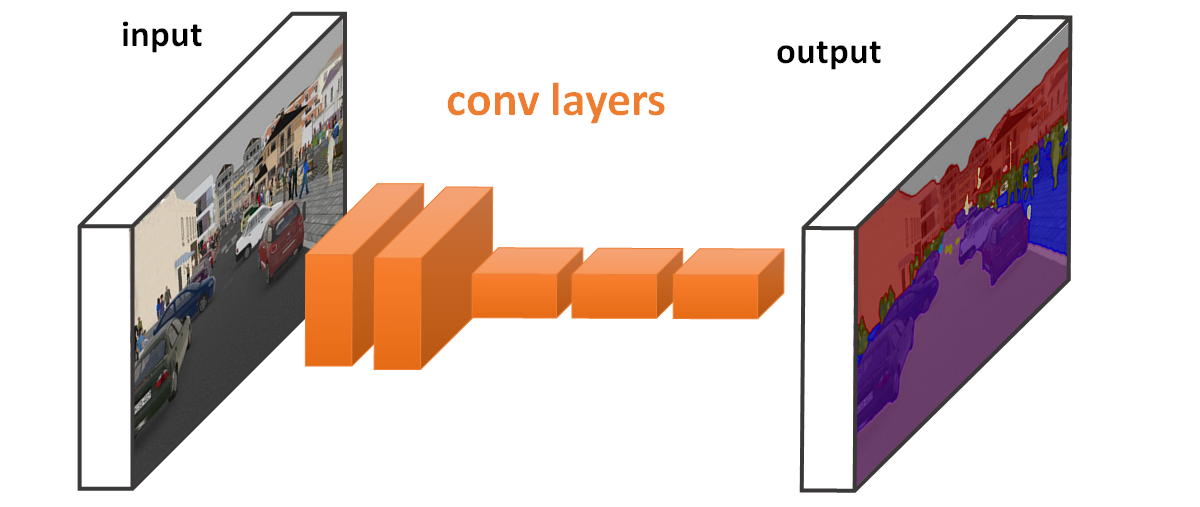
Fuente: Efficient method for running Fully Convolutional Networks (FCNs)

Los ejemplos incluyen datos de series temporales, que pueden puede considerarse como una cuadrícula 1D que toma muestras a intervalos de tiempo regulares o datos de imagen, que puede considerarse como una cuadrícula de píxeles en 2D.

Fuente: Deep Learning for Time Series Classification: a brief overview

El nombre "red neuronal convolucional" indica que la red emplea una operación matemática llamada convolución. La convolución es un tipo especializado de operación lineal. Las redes convolucionales son simplemente redes neuronales que utilizan convolución en lugar de una matriz general en al menos una de sus capas.

¿Qué es una Convolución? ¶

Fuente Nasa

Vamos a usar un ejemplo hipotético para introducir el concepto matemático de convolución. Supongamos que estamos rastreando la ubicación de una nave espacial con un sensor láser. Nuestro sensor láser proporciona una salida única $x (t)$, la posición de la nave espacial en el momento $t$. Tanto $x$ como $t$ tienen un valor real, es decir, podemos obtener una lectura diferente del láser sensor en cualquier instante en el tiempo.

Ahora suponga que nuestro sensor láser es algo ruidoso. Para obtener una estimación menos ruidosa de la posición de la nave espacial, una buena idea es promediar varias mediciones. Por supuesto, las mediciones más recientes son más relevantes, por lo que lo haremos un promedio ponderado que otorgue más peso a las mediciones recientes.

Podemos construir tal promedio ponderado con una función de ponderación $w (a)$, donde $a$ es la edad de una medición. Si aplicamos una operación promedio ponderada en cada momento, obtenemos una nueva función que proporciona una estimación suavizada de la posición $s$ de la nave espacial:

$$s(t) = \int x(a) w(t-a)da$$

Observe que si $a_1.\ldots, a_n$ es una muestra de la distribución cuya función de densidad es $w$, entonces se tiene que

$$s(t)\approx \tfrac{1}{n}\sum_{i=1}^n x(a_i) w(t-a_i)$$

Esta operación se llama convolución. La operación de convolución es típicamente denotada con un asterisco:

$$s(t) = (x ∗ w)(t)$$

En el ejemplo, $w$ debe ser una función de densidad de probabilidad válida, o el el resultado no es un promedio ponderado. Veamos un pequeño ejemplo en acción:

Fuente: Boxcar smoothing with AstroPy

Sin embargo, podemos hacer convoluciones con funciones más generales. La fórmula matemática de la convolución de dos funciones es

$$(f * h)(t)=\int_{-\infty}^{\infty}f(\tau)h(t-\tau)d\tau$$

Y se puede usar para, por ejemplo, suavizar bordes de diferentes señales, como vemos a continuación:

Fuente: What is the phyical significance of convolution?

Fuente:Medical Imaging Systems: An Introductory Guide

A pesar de esto, mantendremos nuestra notación anterior para indicar lo siguiente:

Terminología:

1. $x$ es la entrada input.
2. $w$ es el kernel de la convolución.
3. $s$, la salida, es el feature map.

Por otro lado, es claro que en la vida real no contamos con almacenamiento de información continua, por lo que el concepto de convolución debe usarse de manera discreta (o por medio de muestreos continuos de la señal que está siendo medida):

$$s(t) = (x ∗ w)(t) \approx \sum_{a=-\infty}^{\infty} x(a)w(t-a)$$

[Volver al Inicio]

Uso en Procesamiento de Imágenes ¶

Las convoluciones son muy útiles en la ciencia y la ingeniería y se pueden consultar aqui algunas de ellas. En las próximas sesiones, nos enfocaremos en su uso para crear redes neuronales convolucionales tanto en clasificación como en predicción. Tal vez, una de las aplicaciones más usadas en el Aprendizaje de Máquina, es su uso sobre imágenes y en series de tiempo.

Sí, es posible extender el concepto de convolución a objetos en dos o más dimensiones, como es el caso de una fotografía a color o videos.

Si pensáramos en el mismo proceso anterior pero en 2D, podríamos obtener una fórmula como la siguiente: ​

$$S (i, j) = (I ∗ K) (i, j) = \sum_ {m} \sum_ {n} I (m, n) K (i-m, j-n).$$ ​ Donde I denota la Imagen en cada pixel $m,n$ y $K$ representa el Kernel trasladándose a lo largo y ancho de la imagen $I$.

Conmutatividad:

La convolución es conmutativa. Podemos escribir

$$S (i, j) = (K ∗ I) (i, j) = \sum_ {m} \sum_ {n} I (i-m, j-n) K (m, n).$$

Esta propiedad es conveniente para el estudio matemático de convoluciones.

Correlación Cruzada:

Por otro lado, muchas bibliotecas de redes neuronales implementan un función relacionada llamada correlación cruzada, que es lo mismo que convolución pero sin voltear el kernel:

$$S (i, j) = (I ∗ K) (i, j) = \sum_m \sum_n I (i + m, j + n) K (m, n).$$

Muchas bibliotecas de aprendizaje automático implementan correlación cruzada pero la llaman convolución. Haremos lo mismo.

Ejemplo:

Recordemos que una imagen es un tensor, el cual en algunos casos se puede visualizar por completo:

Fuente: Gentle Dive into Math Behind Convolutional Neural Networks

De la fórmula a la práctica, la convolución de un kernel específico se vería así:

Fuente: Gentle Dive into Math Behind Convolutional Neural Networks

Ejemplos Reales clásicos¶

Redes Neuronales Convolucionales¶

¿Cómo se aplican entonces las convoluciones en una red neuronal? observemos la estructura de una CNN

Capa Convolucional¶

Recordemos un poco cómo funcionan los perceptrones

Fuente: Fouzia Altaf, researchgate.net

Entran datos, se hace la suma de pesos y se aplica la función de activación. Lo que hace la red en cada entrenamiento es encontrar los pesos adecuados para obtener la mejor información posible.

Es posible aplicar esta misma idea al hacer una convolución

Fuente: Fouzia Altaf, researchgate.net

Convoluciones en detalle¶

Caso simple: kernels¶

La imagen muestra los objetos básicos que intervienen en una convolución:

• la imagen,
• el kernel.

Fuente: aprendemachinelearning.com

El gif muestra la forma como se calcula la convolución paso a paso. A la derecha se observa la imagen resultante de la convolución. Por ejemplo el elemento en posición (0,0) se obtiene mediante el siguiente cálculo

• $0 * 1 + 0 * 0 + 0 * (-1) + 0 * 2 + 0 * 0 + 0.6 * (-2) + 0 * 1 + 0.6 * 0 + 0 * (1-) = -1.2$

Fuente: aprendemachinelearning.com

Al final de la lección veremos cómo expresar el cálculo completo como un producto matricial, con lo que se tiene un módulo neuronal clásico si se suma el sesgo (bias) y se aplica la función de activación. La siguiente imagen muestra el proceso completo usando la activación ReLU.

Fuente: aprendemachinelearning.com

Caso con varios canales: Filtros¶

¿Qué hacemos cuando tenemos una imagen a color?

Como hemos visto hasta ahora, los kernels 2D se aplican a imágenes 2D, que por convención, están representadas por tensores bidimensionales de un canal de color. Pero ¿Qué ocurre si el tensor de entrada es 3D?. Es decir, tenemos imágenes 2D con tres canales de color. Este es el caso de por ejemplo, si el tensor de entrada representa a una imagen en formato RGB.

El problema puede plantarse de manera más general en realidad. Supongamos que tenemos tensores de entrada 3D, en donde la tercera dimensión representan diferentes canales, digamos 256 canales.

El truco que usaremos se llama filtro. Lo que vamos a hacer es usar un kernel 2D por cada canal. Entonces, si se tienen 3 canales, usaremos 3 kernels 2D, uno por cada canal. Si tenemos 256 canales, usaremos 256 kernels 2D. Supongamos que en general tenemos d canales. El conjunto de los d kernels 2D que se aplicaran al tensor de tamaño $h*k*d$ se denomina un filtro 2D. Revise detenidamente la siguiente imagen.

Fuente: Alvaro Montenegro

Como puede darse cuenta, sucede los siguiente:

1. El tensor de entrada es de tamaño 4x4x3, el cual se puede interpretar como una imagen de tamaño 4x4 a color, con 3 canales de color.
2. EL filtro tiene tamaño 2x2x3, que corresponde a 3 kernels de tamaño 2x2.
3. Cada kernel se aplica a un canal diferente. Por ejemplo el kernel 1 se aplica al canal 1, haciendo la respectiva convolución. Esta convolución da origen a un mapa de características (features) de tamaño 3x3. Entonces le filtro completo produce un tensor de tamaño 3x3x3, que corresponde a tres mapas de características, cada una de de tamaño 3x3 .
4. Finalmente, los mapas de características se suman componente a componente dando origen al resultado definitivo de la convolución que es un tensor de tamaño 3x3x1.

Múltiples filtros ¶

Ahora vemos la acción de varios filtros sobre la misma imagen. El tensor original tiene tamaño 663 y cada filtro es un tensor de tamaño 3x3x3. En consecuencia Cada filtro da origen a un canal de tamaño 441, se explicó arriba.

Observe que como son tres filtros, y como cada filtro da origen a un cana, la aplicación de los tres filtros da como resultado un tensor de tamaño 4x4x3, es decir imágenes de tamaño 4x4 y tres canales.

Como puede imaginar, a la salida de una capa convolucional 2D, se tienen imágenes en varios canales. Por lo que es posible ver tales imágenes por cada canal. Haremos esto en la próxima lección.

Fuente: Gentle Dive into Math Behind Convolutional Neural Networks

En este caso, el resultado final de la convolución se conoce como filtro. Note que en realidad se hicieron tres convoluciones.

Note que a pesar de ser una operación entre tensores de dimensión 3, el resultado es un tensor de dimensión 2.

La fórmula que explica las dimensiones de salida es:

$$[n,n,n_c]*[f,f,n_c]=\biggl[\text{floor}\biggl({\frac{n+2p-f}{s}+1}\biggr),\text{floor}\biggl({\frac{n+2p-f}{s}+1}\biggr),n_f\biggr]$$

Importante recordar que cada kernel usado resultará en un filtro diferente y disyunto:

Fuente: Applied Deep Learning - Part 4: Convolutional Neural Networks

[Volver al Inicio]

Relleno (Padding)¶

Al hacer nuestro proceso de convolución, se generan cierta pérdida de información debida a las esquinas de la imagen. De hecho, la imagen convolucionada sufre un cambio de dimensión a la baja.

Por lo tanto, la posición de un pixel en la imagen juega un papel fundamental, como se ilustra a continuación:

Fuente: Gentle Dive into Math Behind Convolutional Neural Networks

Para arreglar dicho problema, podemos por ejemplo, agregar una frontera extra de ceros al borde la imagen.

Dicho proceso es conocido como relleno de ceros o zero-padding.

Fuente: Redes Neuronales Convolucionadas (RNC)

En el lenguaje de convoluciones, usualmente se usan dos modos:

• Valid: Regresa la imagen con el kernel convolucionado sin cambios (reduce dimensión de salida).
• Same: Regresa la imagen con el mismo tamaño que la imagen original.

En el caso de hacer padding y usar same, el padding debe cumplir la siguiente ecuación:

$$p=\frac{f-1}{2}$$

donde $p$ es el tamaño de relleno (padding) y $f$ es la dimensión del kernel.

[Volver al Inicio]

Saltos (Strides) ¶

En algunos casos, no queremos tantos detalles sobre la convolución (por ejemplo, si no hay tantos detalles de pixel en pixel). Por ejemplo en imágenes en donde los colores van cambiando muy poco de pixel a pixel. En estos casos, es grato que podemos tener en nuestras redes convolucionadas el parámetro de salto ó stride:

Fuente: Gentle Dive into Math Behind Convolutional Neural Networks

En este caso, la fórmula asociada a la dimensión de salida es:

$$n_{out}=\text{floor}\biggl({\frac{n_{in}+2p-f}{s}+1}\biggr)$$

,

en donde $s$ es el tamaño del salto(stride).

[Volver al Inicio]

Submuestreo. Agrupamiento (Pooling) ¶

Además de las capas convolucionadas, muchas veces es usada la operación llamada pooling para reducir el tamaño del tensor y volver más rápido el procesamiento.

Además, esto reduce el número de parámetros y un número menor de parámetros evita el sobre ajuste.

Estas capas son bastante sencillas. Una vez definidos los hiperparámetros de salto y tamaño de kernel, tenemos fundamentalmente dos tipos de pooling:

• Max Pooling: Divide la imagen en diferentes regiones y toma el valor máximo de dicha región.

Fuente: Redes Neuronales Convolucionadas (RNC)

Fuente: Gentle Dive into Math Behind Convolutional Neural Networks

• Average Pooling: Divide la imagen en diferentes regiones y toma el valor promedio de dicha región.

Fuente: Average-Pooling

Reducción en el número de parámetros¶

Como se podrán haber dado cuenta, una red densamente conectada (DNN) no son la mejor opción al momento de trabajar con imágenes, dada la cantidad tan enorme de parámetros que deben ser aprendidos.

Para entender el verdadero poder de las convoluciones, note la siguiente imagen:

Fuente: Gentle Dive into Math Behind Convolutional Neural Networks

Vemos claramente que !no todas las neuronas están conectadas entre sí!

Además, que algunas neuronas comparten los mismos pesos.

Esto significa que una red neuronal convolucionada tiene muchos menos parámetros para aprender.

[Volver al Inicio]

Arquitectura de las redes neuronale convolucionales ¶

La siguiente imagen ilustra una arquitectura convolucinal muy general.

Fuente: aprendemachinelearning.com

Aquí encontramos la arquitectura de red convolucional clásica. Observe como cada mapa de features es mas pequeño que en la capa anterior, pero a su vez hay precencia de más filtros. No se muesyran, pero a la salida de cada capa convolucional siempre hay una activación presente.

Fuente: Applied Deep Learning - Part 4: Convolutional Neural Networks

Finalmente vemos la arquitectura de una red convolucional profunda.

En efecto, es una de las arquitecturas más famosas de la historia de la redes convolucionales, conocida como VGG

Fuente:Applied Deep Learning - Part 4: Convolutional Neural Networks

Convoluciones 1D y 3D¶

En esta lección hemos estudiado convoluciones 2D. Partimos de la hipótesis que tenemos imágenes de tamaño $h\times k$ en $d$ canales. En términos tensoriales tenemos a la entrada tensores de tamaño $h\times k \times d$. Al aplicar convoluciones 2D a estos objetos, la tercera dimensión se interpreta como un canal. Entonces usamos $m$ filtros de tamaño $k_1\times k_2 \times d$ dando origen a tensores de tamaño $h'\times k' \times m$. Es decir el resultado global de la convolución 2D es un tensor de dimensión 3.

Convoluciones 1D¶

Ahora solamente tiene un sentido claro, aplicar kernels de tamaño $k_1 \times 1$ y en consecuencia filtros de tamaño $k_1\times k_2, m$. La siguiente imagen ilustra la situación con un único filtro $m=1$.

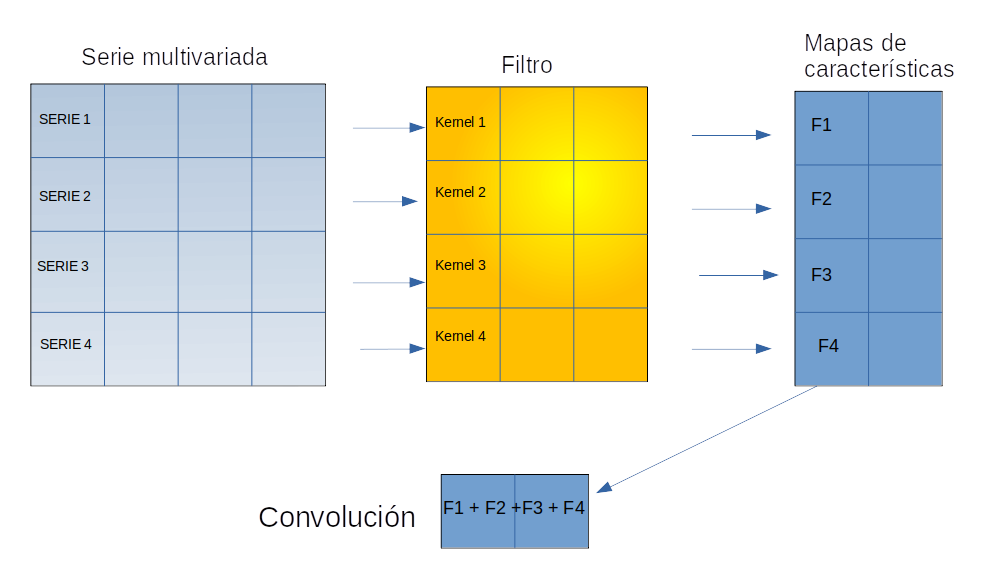
Fuente: Alvaro Montenegro

Ejercicio¶

1. Describa como puede combinar las convoluciones 1D con LSTM o GRU.
2. ¿ Se requiere la ventana deslizante en este caso?
3. ¿Cual es la dimensión del tensor de salida en una convolución 1D?

Convoluciones 3D¶

Finalmente llegamos al caso más complejo. El caso de las convoluciones 3D. Nuestro problema básico es que ahora no es posible representar fácilmente el resultado de la convolución 3D, debido a que es un tensor de dimensión 4.

En las convoluciones 3D, suponemos que se tienen tensores de entrada de tamaño $h\times k \times l \times t$. La última dimensión corresponde a los canales. En el caso de los videos, cana canal corresponde a un frame del video. Por lo tanto, si el video consta de 10000 frames, se tienen 10000 canales.

Los kernels en esta caso son tridimensionales de tamaño $k_1\times k_2 \times k_3$ y los filtros son de tamaño $k_1\times k_2 \times k_3 \times m$. La imagen ilustra un kernel 3D.

Fuente: towardsdatascience.com

Ejercicio¶

Suponga que se tiene un video de tamaño 1000 frames, cada uno con imágenes de tamaño 512 x 512 en RGB. Ahora suponga que aplica 100 filtros de tamaño 5x5x5.

1. ¿Cuál es el tamaño del tensor de entrada y del tensor de salida?
2. ¿Cómo interpretar cada canal de salida?
3. ¿Si se intentara visualizar un canal de salida como lo haría?

Representación matricial de las convoluciones¶

Por facilidad supongamos que se tiene una imagen de tamaño $4\times 4$ y un kernel de tamaño $3\times 3$, el cual se usuara para hacer una convolución a la imagen, sin padding y strides =1. La imagen resultate tien tamaño $2\times 2$. ¿Por qué?

La imagen ilustra la situación

Fuente: ai.stackexchange.com

El kernel es representado por la matriz

$$\mathbf{W} = \begin{pmatrix} w_{00} & w_{01} & w_{02}\\ w_{10} & w_{11} & w_{12}\\ w_{20} & w_{21} & w_{22}, \end{pmatrix}$$

y la imagen puede ser vista como

$$\mathbf{I} = \begin{pmatrix} i_{00} & i_{01} & i_{02} & i_{03}\\ i_{10} & i_{11} & i_{12} & i_{13}\\ i_{20} & i_{21} & i_{22} & i_{23}\\ i_{30} & i_{31} & i_{32} & i_{33} \end{pmatrix}$$

Si reescribimos el kernel de la siguiente forma

$$\mathbf{W'} = \begin{pmatrix} w_{00} & w_{01} & w_{02} & 0 & w_{10} & w_{11} & w_{12} & 0 & w_{20} & w_{21} & w_{22} &0 &0 &0 &0 &0 \\ 0& w_{00} & w_{01} & w_{02} & 0 & w_{10} & w_{11} & w_{12} & 0 & w_{20} & w_{21} & w_{22} &0 &0 &0 &0 \\ 0 & 0 & 0 & 0& w_{00} & w_{01} & w_{02} & 0 & w_{10} & w_{11} & w_{12} & 0 & w_{20} & w_{21} & w_{22} &0 \\ 0 & 0 & 0 & 0 & 0 & w_{00} & w_{01} & w_{02} & 0 & w_{10} & w_{11} & w_{12} & 0 & w_{20} & w_{21} & w_{22} \end{pmatrix}$$

y la imagen como

$$\mathbf{I'} = \begin{pmatrix} i_{00} & i_{01} & i_{02} & i_{03} & i_{10} & i_{11} & i_{12} & i_{13}& i_{20} & i_{21} & i_{22} & i_{23}& i_{30} & i_{31} & i_{32} & i_{33} \end{pmatrix}$$

El resultado de la convolución es

$$\mathbf{C} = \mathbf{W'} \times \mathbf{I'}$$

en donde

$$\mathbf{C} = \begin{pmatrix} c_{00} & c_{01} & c_{10} & c_{11}\end{pmatrix},$$

la cual por supuesto se puede reescribir como

$$\mathbf{C} = \begin{pmatrix} c_{00} & c_{01}\\ c_{10} & c_{11}\end{pmatrix}.$$

En consecuencia, la convolución es realmente un módulo neuronal de tipo perceptron con con una configuración de pesos especial.

Promedios móviles y submuestreo¶

Como ejercicio final, le invitamos a pensar en las siguientes dos afirmaciones:

1. Las convoluciones representan promedios móviles uni, bi o tridimensionales, segun el caso.
2. El pooling es una forma de submuestreo de la imagen. De cada región en la cual se divide la imagen para hacer el pooling, se toma un resumen. Este proceso que puede interpretarse como un submuestro de la imagen.
3. Un promedio móvil crea un efecto de suavizado y reduce el ruido de las fluctuaciones de los objetos.
4. El pooling permite mantener elementos escenciales de los objetos descartando informacion redundante.