HDS-LEE Course on Hyperparameter Optimization - Part 2¶

This notebook summarizes several examples from the Talos GitHub repository. The original examples can be found on https://github.com/autonomio/talos/tree/master/examples

Note: The output of this notebook is not reproducible. This means that the final output changes with every usage of the code. There are two main reasons for this stochastic behavior:

the traing set is quite small (400 samples) to reduce computing time (this is a tutorial so that

there is a limited amount of time)

we use a 'random hyperparameter search strategy' and only cover a small percentage

of parameter configurations (about 1%) to reduce computing time so that the output, of course, is not deterministic.

In practice, this stochastic behavior should be strongly reduced since the number of training samples is usually much larger and the 'random hyperparameter search strategy' usually covers a larger percentage of hyperparameter configurations.

In [ ]:

%matplotlib inline
# required Talos __version__ = "0.6.6"
import talos
import numpy as np

Overview¶

The aim of the 2nd tutorial is the following:

Introduction of Talos
Use Talos for machine-assisted hyperparameter optimization of the Boston house pricing problem (1st Jupyter notebook).

Also note that there is a large variety of hyperparameter tuning libraries and Talos is only one viable option (another recommend alternative is Keras Tuner)

Give general guidelines on hyperparameter optimization

Table of Contents¶

1. Introduction of Talos

2. Use Talos for hyperparameter optimization

3. Guidelines on hyperparameter optimization

1. Introduction of Talos ¶

Restore the original Keras code¶

We start with the code that we have already used in the first notebook

In [ ]:

from keras.datasets import boston_housing

# load the data
(train_data, train_targets), (test_data, test_targets) =  boston_housing.load_data()

# data normalization
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std

test_data -= mean
test_data /= std

Model preparation¶

Talos works with any Keras model, without changing the structure of the model in any way.
The only difference in the Keras model is that a parameter is not set explicitly as before, e.g.

 model.add(layers.Dense(32, activation='relu'))

but instead taken from a dictionary, e.g.


params = {'number_of_neurons' : [4, 6, 7, 8], 'activation' : ['relu'] }

model.add(layers.Dense(params['number_of_neurons'], activation=params['activation']))

Afterwards, this dictionary and the model will be passed to Talos. In the dictionary we have three different ways to input values:

as stepped ranges (min, max, steps) if the parameter is a floating point number
as multiple values [in a list]
as a single value [in a list]

For values we don't want to use, it's ok to set it as None.

Tasks¶

Excercise 1:

Create a Python dictionary that contains at least the following entries:
- 'number_of_layers' : 1, 2
- 'number_of_neurons' : 8, 16, 32, 64
- 'dropout_value' : None, 0.1, 0.2
- 'optimizer' : 'Adam', 'rmsprop'
- 'batch_size': 1, 2, 4, 8
- 'epoch_number' : 10, 20, 40, 80
- anything that you want to modify further (e.g. learning_rate, activation_function, loss_function, ...)
What is the number of different hyperparameter configurations that is considered in the first six bullet points?

Answer: 768 different configurations.

In [ ]:

# parameter dictionary
param = {'number_of_layers' : [1, 2],
         'number_of_neurons' : [8, 16, 32, 64],
         'epoch_number' : [10, 20, 40, 80],
         'dropout_value' : [None, 0.1, 0.2],
         'optimizer' : ['Adam', 'rmsprop'],
         'batch_size' : [1, 2, 4, 8]}

Tasks¶

Excercise 2:

Modify your original Keras model (Jupyter notebook 1) such that it uses uses the values from a

dictionary 'p'.

In [ ]:

from keras import models
from keras import layers

# note: this build model works for a limited number of hidden layers, there are other options in Talos
# if you are interested in a large number of layers (see: Outlook at the end of this tutorial)
def build_better_model(x, y, val_data, val_targets, p):
    model = models.Sequential()
    
    # replace the hyperparameter inputs with references to dictionary p 
    model.add(layers.Dense(p['number_of_neurons'], activation='relu',
                           input_shape=(x.shape[1],)))
    
    if p['number_of_layers'] >= 2:
        model.add(layers.Dense(p['number_of_neurons'], activation='relu'))
    
    if p['dropout_value'] is not None:
        model.add(layers.Dropout(p['dropout_value']))
        
    model.add(layers.Dense(1))
    model.compile(optimizer=p['optimizer'], loss='mse', metrics=['mae'])
    
    # make sure history object is returned by model.fit()
    history = model.fit(x, y, epochs=p['epoch_number'], batch_size=p['batch_size'], verbose=0)
    
    return history, model

2. Use Talos for hyperparameter optimization ¶

This part is quite simple. The Talos experiment just uses the Scan() command. In the following, we will investigate different arguments for this routine. However, there are only five necessary arguments that are required:

train_data (often known as 'x')
train_targets (often known as 'y')
params (the dictionary 'param' that we have created before)
model (the 'build_model' that we also have created before)
experiment_name (name of a folder in which the output, a csv-file, is stored)

In [ ]:

scan_object = talos.Scan(x=train_data,
                         y=train_targets,
                         model=build_better_model,
                         experiment_name='find_optimal_params',
                         params=param,
                         round_limit=10)

If all different parameter configurations from the dictionary are used, the routine Scan() has to evaluate 768 different models. Depending on the neural network architecture and the number of training samples, this can be very time-consuming.

As a solution, Talos offers several routines to limit the number of model configurations that is evaluated. Two useful commands of Scan() for this purpose are:

round_limit=10 which limits the number of model evaluations to the specified integer value (e.g.

10 model evaluations in this example).

fraction_limit = 0.1 specifies the fraction of params that will be tested (e.g. 10% of the

configurations in this example).

Access the results through the `Scan` object¶

Using round_limit=10 we have investigated only ten parameter configurations (about 1% of all possible configurations) since the time for this tutorial is limited. But what are ten configurations that have been used and what is their performance?

For this purpose, the results of the scan object can be directly accessed:

In [ ]:

# accessing the results data frame
scan_object.data

The output on my local computer is (the results should differ on your machine since you consider ten other random parameter configurations)

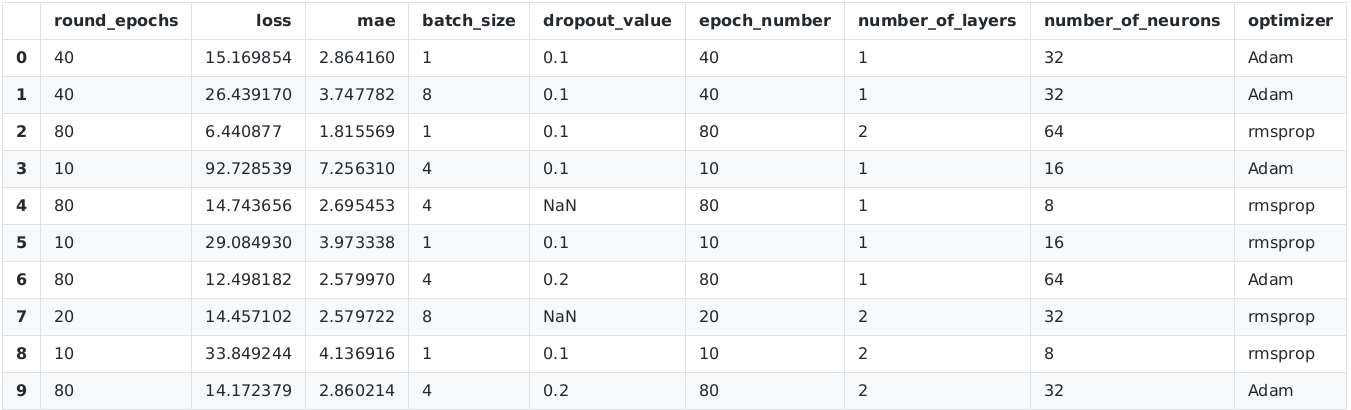
There are several hyperparameter configurations with a mean average error (mae) in the range 2-3 (i.e. the average house pricing error is 2000-3000 dollar). Since the number of training samples is only 400, the results of the mean average error have a high variance and should not be overestimated. Nevertheless, we already obtain a certain understanding of a sensible size of some of the hyperparameters (e.g. 10 epochs is certainly not enough since 'mae' becomes large then).

You already noticed that your results differ from mine. This is due to the usage of a 'random search' strategy in Talos. More information on the search strategy are given in the summary details using scan_object.details.

In [ ]:

# access the summary details
scan_object.details

From the 768 possible hyperparameter configurations Talos considers a random subset of ten configurations (due to round_limit=10). This random subset is chosen with a 'Mersenne Twister' pseudorandom number generator. Other possible random choices in Talos are, for instance, 'Halton' or 'Sobol' quasi Monte Carlo sequences.

Note: If there is no parameter such as round_limit=10 or fraction_limit = 0.1 the default optimization strategy is called 'grid search'. This means that all hyperparameter permutations in a given dictionary are processed. In most cases, this is not recommended for anything but very small permutation spaces. Therefore, better use a 'random search' routine.

In addition to statistics and meta-data related with the Scan, the used data (x and y) together with the saved model and model weights for each hyperparameter permutation is stored in the Scan object.

In [ ]:

# accessing the saved models which returns a list of models
# scan_object.saved_models

In [ ]:

# accessing the saved weights for models which returns a list of weights
model_weights = scan_object.saved_weights

# weights of first model 
model_weights[0]

The Scan object can be further used, and is required, as input for Predict(), Evaluate(), and Deploy(). More about this in the corresponding sections below.

Analysing the Scan results with `Reporting()`¶

In the Scan process, the results are stored round-by-round in the corresponding experiment log which is a .csv file stored in the output directory (which is './find_optimal_params' our case). The Reporting() accepts as its source either a file name, or the Scan object.

In [ ]:

# use Scan object as input
analyze_object = talos.Analyze(scan_object)

In [ ]:

# get the number of rounds in the Scan
analyze_object.rounds()

In [ ]:

# get the lowest result for any metric (if lower is better)
analyze_object.low('mae')

Next, we want to know the parameters of our best n=3 parameter runs. For this purpose we use best_params. It is alluring to consider the best result only (i.e. n=1 in the following cell) but keep in mind that due to the high variance in the result, a sequence of more models should be considered.

The signature of best_params() is the following:

The first argument (here 'mae') is the metric that is considered.
The second argument is a list of metrics / loss functions that is not required here
The third argument gives the 'n' best results
Fourth argument: ascending | bool | Set to True when metric is to be minimized eg. loss or mae

In [ ]:

# get the best n=3 paramaters
analyze_object.best_params('mae', ['loss'], n=3, ascending=True)

It is very important to determine which of your hyperparameters has the largest impact on your performance metric. These are the parameters that should be further investigated.

One solution to achieve this is to compute the linear correlation between your performance metric 'mae' and your hyperparamters. The correlation coefficient is +1 in the case of a perfect direct (increasing) linear relationship, -1 in the case of a perfect decreasing (inverse) linear relationship and some values in (-1, 1) otherwise (indicating the degree of linear dependance between the variables).

We employ correlate() for computing the correlation

In [ ]:

# get correlation for hyperparameters against a performance metric such as 'mae' (we exclude 'loss' since 
# this is not a hyperparameter)
analyze_object.correlate('mae', ['loss', 'round_epochs'])

Since you have only then different hyperparameter runs, the output is almost random. However, in practice with hundreds or thousand of different configurations the result is much less stochastic noise in this output.

In my special case, 'epoch_number' and 'number_of_neurons' have the strongest inverse effect on 'mae' (i.e. 'more epochs tend to lead to a lower mean average error'). The 'batch_size' seems to be less important.

You can also plot a heatmap of this correlation using plot_corr():

In [ ]:

# heatmap correlation
analyze_object.plot_corr('mae', ['loss', 'round_epochs'])

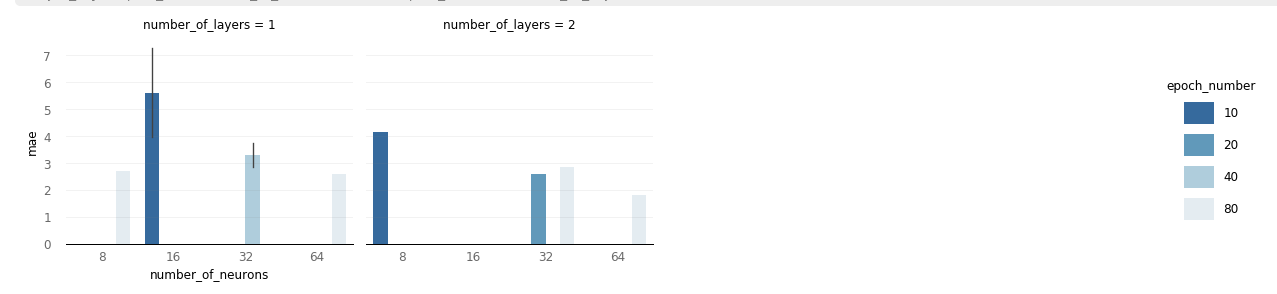
The correlation between variables in one viable way to find the most important hyperparameters. A different approach is given by plot_bars(). Using this function, the metric 'mae' is plotted for different values of the hyperparameters 'number_of_neurons', 'number_of_layers' and 'epoch_number'. As mentioned before, 'mae' seems to decrease for larger values of these hyperparameters (in the specified region of the dictionary).

The bar grid cotanins error bars if there is more than one result for the specified hyperparameter set ('number_of_neurons', 'epoch_number', 'number_of_layers').

In [ ]:

# a four dimensional bar grid
analyze_object.plot_bars('number_of_neurons','mae', 'epoch_number', 'number_of_layers')

My current output plot is

Tasks¶

Excercise 3:

Apply the described process to your Talos output. In more detail:
- Find the hyperparameters that have the largest effect on the performance metric.
- Create a 2nd hyperparameter dictionary that further investigates these important hyperparameters
- Use Scan() to investigate the 2nd dictionary in more detail
(use larger values for round_limit than 10).
- Try to find a close-to-optimal model for this specific regression problem.

In [ ]:

# your new hyperparameter dictionary
param2 = {'number_of_layers' : [1, 2],
         'number_of_neurons' : [8, 16, 32, 64],
         'epoch_number' : [10, 20, 40, 80],
         'dropout_value' : [0.1],
         'optimizer' : ['Adam'],
         'batch_size' : [2]}

In [18]:

scan_object2 = talos.Scan(x=train_data,
                         y=train_targets,
                         model=build_better_model,
                         experiment_name='find_optimal_params',
                         params=param2,
                         round_limit=30)

100%|██████████| 30/30 [02:09<00:00,  4.33s/it]

In [19]:

# if you want to see the full output of Scan()
scan_object2.data

Out[19]:

	round_epochs	loss	mae	batch_size	dropout_value	epoch_number	number_of_layers	number_of_neurons	optimizer
0	20	62.639259	5.708464	2	0.1	20	1	8	Adam
1	20	34.694954	3.966872	2	0.1	20	2	8	Adam
2	20	36.716732	4.228592	2	0.1	20	1	16	Adam
3	10	14.261839	2.705653	2	0.1	10	2	64	Adam
4	20	25.094707	3.387398	2	0.1	20	1	32	Adam
5	40	11.909590	2.507125	2	0.1	40	2	32	Adam
6	40	16.655113	3.039295	2	0.1	40	2	16	Adam
7	10	65.708862	5.513346	2	0.1	10	2	8	Adam
8	80	29.435696	3.740955	2	0.1	80	2	8	Adam
9	10	24.315041	3.535035	2	0.1	10	2	16	Adam
10	20	12.350898	2.560938	2	0.1	20	2	64	Adam
11	40	40.795216	4.784678	2	0.1	40	1	8	Adam
12	80	4.468213	1.586145	2	0.1	80	2	64	Adam
13	40	7.926467	2.032866	2	0.1	40	2	64	Adam
14	80	10.375111	2.368851	2	0.1	80	1	64	Adam
15	10	26.432457	3.684221	2	0.1	10	1	64	Adam
16	10	31.056013	4.031105	2	0.1	10	1	32	Adam
17	40	21.009483	3.343462	2	0.1	40	1	16	Adam
18	40	20.669701	3.241881	2	0.1	40	2	8	Adam
19	20	17.996449	3.113712	2	0.1	20	2	16	Adam
20	10	98.833633	7.474075	2	0.1	10	1	8	Adam
21	80	12.074955	2.582160	2	0.1	80	2	32	Adam
22	80	18.129484	3.213502	2	0.1	80	1	16	Adam
23	80	15.650631	3.000904	2	0.1	80	2	16	Adam
24	80	21.813120	3.371564	2	0.1	80	1	8	Adam
25	10	15.743234	2.941543	2	0.1	10	2	32	Adam
26	40	10.985904	2.432760	2	0.1	40	1	64	Adam
27	40	15.729487	2.934194	2	0.1	40	1	32	Adam
28	20	15.917757	2.919967	2	0.1	20	2	32	Adam
29	10	56.185284	4.956959	2	0.1	10	1	16	Adam

Your best results are:

In [20]:

# use Scan object as input
analyze_object2 = talos.Analyze(scan_object2)

# get the best n=3 paramaters
analyze_object2.best_params('mae', ['loss'], n=3, ascending=True)

Out[20]:

array([[80, 2, 0.1, 2, 64, 'Adam', 80, 0],
       [40, 2, 0.1, 2, 64, 'Adam', 40, 1],
       [80, 1, 0.1, 2, 64, 'Adam', 80, 2]], dtype=object)

In [21]:

# lowest mae with the parameters from analyze_object2.best_params('mae', ['loss'], n=1, ascending=True)
analyze_object2.low('mae')

Out[21]:

1.5861448049545288

Deploy close-to-optimal model¶

Evaluating Models with `Evaluate()`¶

Models can be evaluated with Evaluate() against a k-fold cross-validation (fold=K specifies the number of repetitions in Evaluate()). Ideally at least 50% of the data, or more if possible, is kept completely out of the Scan process and only exposed into Evaluate once one or more candidate models have been identified.

In [22]:

evaluate_object = talos.Evaluate(scan_object2)

# returns a list with 'folds=10' outputs
all_mae_results =  evaluate_object.evaluate(test_data, test_targets, folds=10, metric='mae', task='continuous')

# this is the average 'mae' that gives an aedequate estimation of our model error (on the test data)
np.mean(all_mae_results)

Out[22]:

7.544865637779236

Once a sufficiently performing model has been found, a deployment package can be easily created.

Deploying Models with `Deploy()`¶

Once the right model or models have been found, you can create a deployment package with Deploy() which is then easy to transfer to a production or other environment, send via email, or upload to shared remote location. Best model is automatically chosen based on a given metric ('val_acc' by default).

The Deploy package is a zip file that consist of:

details of the scan
model weights
model json
results of the experiment
sample of x data
sample of y data

The Deploy package can be easily restored with Restore() which is covered in the next section.

In [23]:

# creates a file waw_regression_deploy.zip (\approx 13 KB) in the local folder 
# the parameter 'asc' has to be true if lower means better (e.g. loss, mae) but false otherwise (e.g. accuracy)
talos.Deploy(scan_object=scan_object2, model_name='waw_regression_deploy', metric='mae', asc=True);

---------------------------------------------------------------------------
FileExistsError                           Traceback (most recent call last)
<ipython-input-23-7dc207c7fec7> in <module>
      1 # creates a file waw_regression_deploy.zip (\approx 13 KB) in the local folder
      2 # the parameter 'asc' has to be true if lower means better (e.g. loss, mae) but false otherwise (e.g. accuracy)
----> 3 talos.Deploy(scan_object=scan_object2, model_name='waw_regression_deploy', metric='mae', asc=True);
      4 

~/anaconda3/envs/Hyperparameter_tutorial/lib/python3.7/site-packages/talos/commands/deploy.py in __init__(self, scan_object, model_name, metric, asc)
     28 
     29         self.scan_object = scan_object
---> 30         os.mkdir(model_name)
     31         self.path = model_name + '/' + model_name
     32         self.model_name = model_name

FileExistsError: [Errno 17] File exists: 'waw_regression_deploy'

Restoring Models with `Restore()`¶

In [ ]:

waw_regression = talos.Restore('waw_regression_deploy.zip')

The Restore object now consists of the assets from the Scan object originally associated with the experiment, together with the model that had been picked as 'best'. The model can be immediately used for making prediction, or use in any other other way Keras model objects can be used.

In [ ]:

# What is the 'best' model that we use for predictions?
# this should be the same model as found with (better check this) 
# 'analyze_object2.best_params('mae', ['loss'], n=1, ascending=True)' from the previous cell 
waw_regression.model.get_config()

In [ ]:

# make predictions with the model
# if you are interested, compare the output with the ground truth 'test_targets'
waw_regression.model.predict(test_data)

In addition, for book keeping purpose, and for simplicity of sharing models with team members and other stakeholders, various attributes are included in the Restore object:

In [ ]:

# get the meta-data for the experiment
waw_regression.details

In [ ]:

# get the hyperparameter space boundary, these are the hyperparameter values that you have considered before
waw_regression.params

In [ ]:

# these are the results from the different runs of Scan()
waw_regression.results

That's almost all on Talos for today. Of course, there are several other routines that are provided by Talos. You find the most recent version (0.6.4 in November 2019) on GitHub (https://github.com/autonomio/talos).

Outlook: a large numbers of hidden layers in Talos¶

You probably have noticed that our model architecture in 'def build_better_model()' can only be used for a relatively low number of hidden layers (since you have to add each layer manually). For a larger number of hidden layers, Talos provides a 'hidden_layers' model (https://github.com/autonomio/talos/blob/master/docs/Hidden_Layers.md). When 'hidden_layers' are used, several parameters must be included in your parameter dictionary. These parameters are 'dropout', 'shapes', 'hidden_layers', 'first_neuron' and 'activation'.

An application for our problem might look like this:

In [ ]:

param = {'hidden_layers' : [1, 2],          # <--- required
         'first_neuron' : [8, 16, 32, 64],  # <--- required
         'dropout' : [0, 0.1, 0.2],         # <--- required
         'shapes': ['brick'],               # <--- required
         'activation': ['relu'],            # <--- required
         'epoch_number' : [10, 20, 40, 80],
         'optimizer' : ['Adam', 'rmsprop'],
         'batch_size' : [1, 2, 4, 8]}

In [ ]:

from keras import models
from keras import layers
from talos.utils import hidden_layers

def build_even_better_model(train_data, train_targets, val_data, val_targets, p):
    model = models.Sequential()
    
    hidden_layers(model, p, 1) # <--- the required arguments are used here
        
    model.add(layers.Dense(1))
    model.compile(optimizer='Adam', loss='mse', metrics=['mae'])
    
    # make sure history object is returned by model.fit()
    history = model.fit(train_data, train_targets, epochs=p['epoch_number'], batch_size=p['batch_size'], verbose=0)
    
    return history, model

Bonus¶

Excercise 4:

Use the feature 'hidden_layers' from Talos for a new hyperparameter search.

3. Guidelines on hyperparameter optimization ¶

Hyperparameter optimization (at least as described in this tutorial with Talos) is an iterative process. You define the

hyperparamter boundaries and start a search with Scan(). Using the results, you define new hyperparameter boundaries and a second search, ..., ..., final search.

In most situations, it is not necessary to perform a full grid search on all possible hyperparameter

configurations (maybe in the order of thousands). Usually, it is sufficient to perform the scan on a random subset (10-30%).

It is important to determine those hyperparameter that have the largest influence on your performance

metric. For this purpose, Talos provides routine such as correlate() to assist you to find these hyperparameters.

All different hyperparameter combinations are evaluated on a validation set. As usual, only your final (after several iterations)

model is evaluated with a test set that is independent of the validation set.

Even though Talos can be used analyze thousands of hyperparameter configurations, it is important to

first get some kind of intuition/understanding which model architecture might be adequate (e.g. do you require fully connected neural networks?, convolutional neural networks?, what might be the rough number of hidden layers?). Otherwise, since the hyperparameter space grows exponentially you will not be able to evaluate a relevant subset of your high-dimensional hypercube within a reasonable amount of time (cf. Curse of Dimensionality).

Thank you for your participiation!
We hope that you have enjoyed this tutorial.

HDS-LEE Course on Hyperparameter Optimization - Part 2¶

Overview¶

Table of Contents¶

1. Introduction of Talos

2. Use Talos for hyperparameter optimization

3. Guidelines on hyperparameter optimization

1. Introduction of Talos ¶

Restore the original Keras code¶

Model preparation¶

Tasks¶

Tasks¶

2. Use Talos for hyperparameter optimization ¶

Access the results through the Scan object¶

Analysing the Scan results with Reporting()¶

Tasks¶

Deploy close-to-optimal model¶

Evaluating Models with Evaluate()¶

Deploying Models with Deploy()¶

Restoring Models with Restore()¶

Outlook: a large numbers of hidden layers in Talos¶

Bonus¶

3. Guidelines on hyperparameter optimization ¶

Access the results through the `Scan` object¶

Analysing the Scan results with `Reporting()`¶

Evaluating Models with `Evaluate()`¶

Deploying Models with `Deploy()`¶

Restoring Models with `Restore()`¶