Exercise 3.3 - Solution¶
Checkerboard¶
Open the Tensorflow Playground (www.playground.tensorflow.org) and select on the left the checkerboard pattern as the data basis.
The data is taken from a two-dimensional probability distribution and is represented by the value pairs $x_1$ and $x_2$. The regions $x1$, $x_2 > 0$ and $x_1$, $x_2 < 0$ are shown by one color. For value pairs with $x_1 > 0$, $x_2 < 0$ and $x_1 < 0$, $x_2 > 0$, the regions are indicated by a different color.
In features, select the two independent variables $x_1$ and $x_2$ and start the network training. The network learns that $x_1$ and $x_2$ are for these data not independent variables, but are taken from the probability distribution of the checkerboard pattern.
Tasks¶
- Try various settings for the number of layers and neurons using
ReLUas activation function. What is the smallest network that gives a good fit result? - What do you observe when training networks with the same settings multiple times? Explain your observations.
- Try additional input features: Which one is most helpful?
Solutions¶
Hint: click on the images to open the correct playground settings needed to solve the task, respectively.
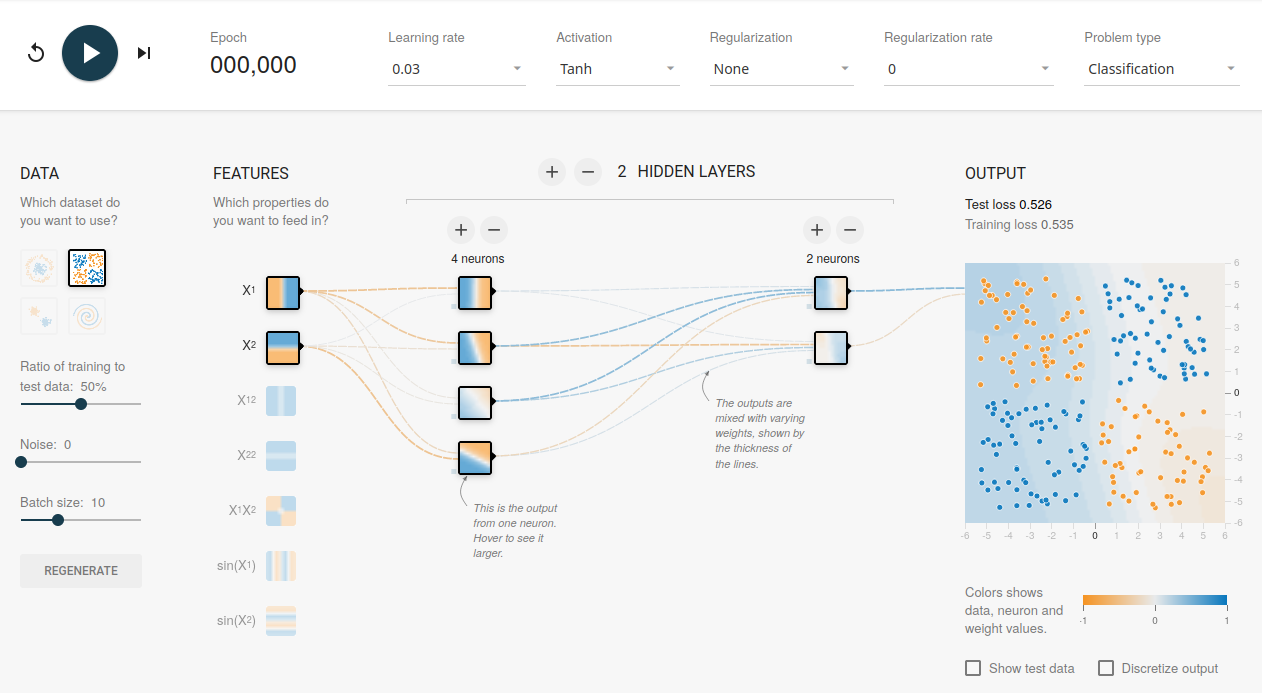
Task 1¶
Try various settings for the number of layers and neurons using ReLU as activation function. What is the smallest network that gives a good fit result?
Task 2¶
What do you observe when training networks with the same settings multiple times? Explain your observations.
Due to the random initialization of weights, the network training always develops a little bit differently, leading to different results.
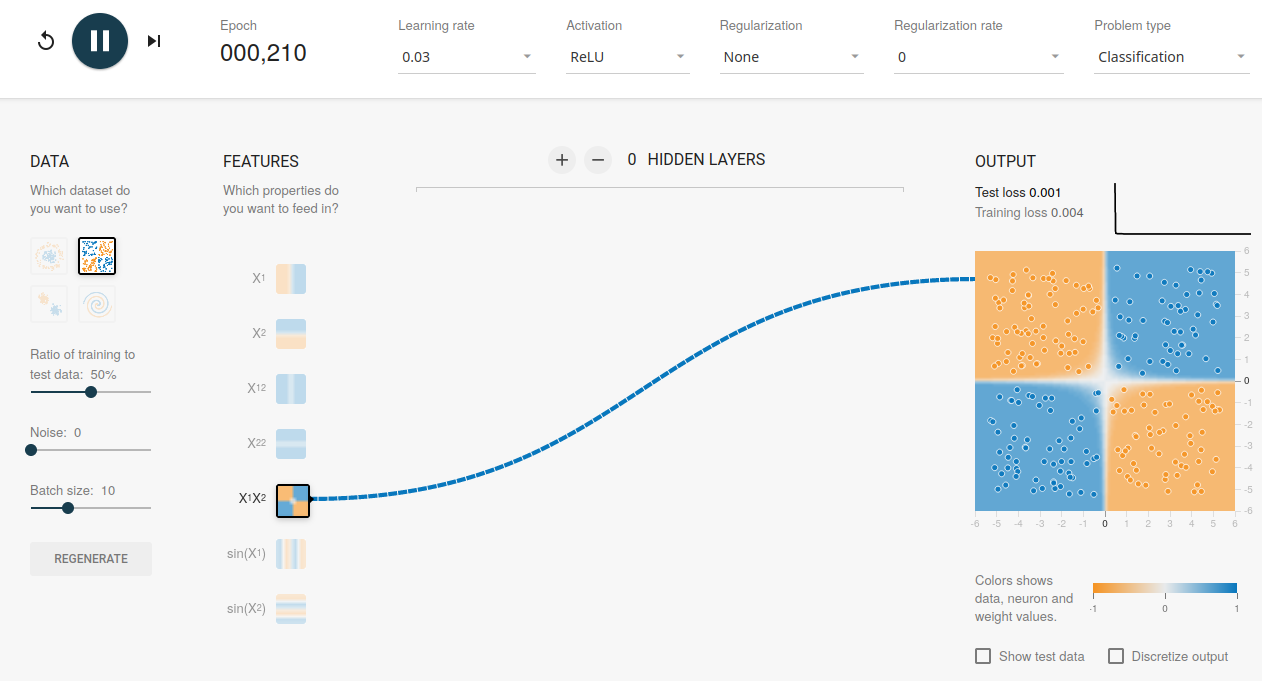
Task 3¶
Try additional input features: Which one is most helpful?