Notebook

Transient heat equation¶

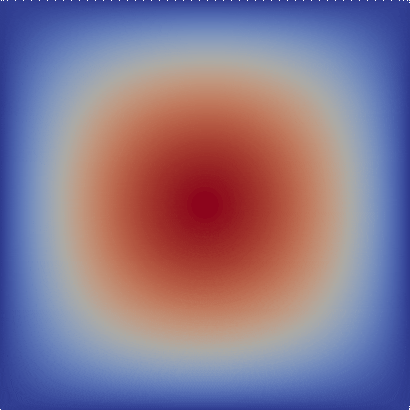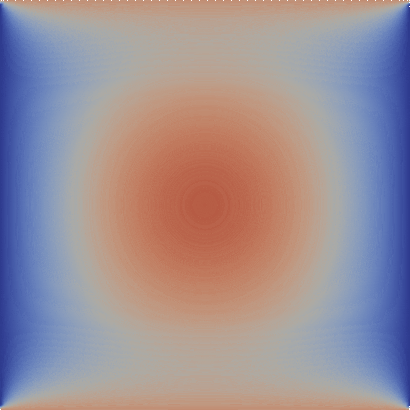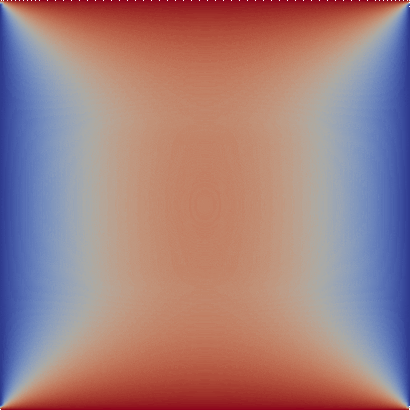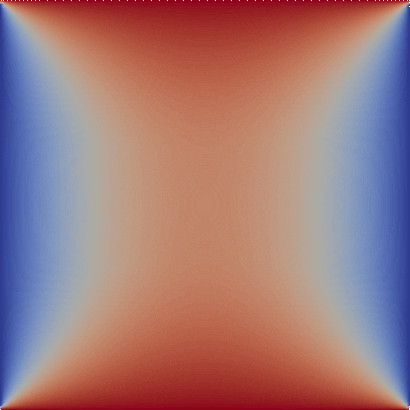
Figure 1: Visualization of the temperature time evolution on a unit square where the prescribed temperature on the upper and lower parts of the boundary increase with time.

Introduction¶

In this example we extend the heat equation by a time dependent term, i.e. $$ \frac{\partial u}{\partial t}-\nabla \cdot (k \nabla u) = f \quad x \in \Omega, $$

where $u$ is the unknown temperature field, $k$ the heat conductivity, $f$ the heat source and $\Omega$ the domain. For simplicity, we hard code $f = 0.1$ and $k = 10^{-3}$. We define homogeneous Dirichlet boundary conditions along the left and right edge of the domain. $$ u(x,t) = 0 \quad x \in \partial \Omega_1, $$ where $\partial \Omega_1$ denotes the left and right boundary of $\Omega$.

Further, we define heterogeneous Dirichlet boundary conditions at the top and bottom edge $\partial \Omega_2$. We choose a linearly increasing function $a(t)$ that describes the temperature at this boundary $$ u(x,t) = a(t) \quad x \in \partial \Omega_2. $$ The semidiscrete weak form is given by $$ \int_{\Omega}v \frac{\partial u}{\partial t} \ \mathrm{d}\Omega + \int_{\Omega} k \nabla v \cdot \nabla u \ \mathrm{d}\Omega = \int_{\Omega} f v \ \mathrm{d}\Omega, $$ where $v$ is a suitable test function. Now, we still need to discretize the time derivative. An implicit Euler scheme is applied, which yields: $$ \int_{\Omega} v\, u_{n+1}\ \mathrm{d}\Omega + \Delta t\int_{\Omega} k \nabla v \cdot \nabla u_{n+1} \ \mathrm{d}\Omega = \Delta t\int_{\Omega} f v \ \mathrm{d}\Omega + \int_{\Omega} v \, u_{n} \ \mathrm{d}\Omega. $$ If we assemble the discrete operators, we get the following algebraic system: $$ \mathbf{M} \mathbf{u}_{n+1} + Δt \mathbf{K} \mathbf{u}_{n+1} = Δt \mathbf{f} + \mathbf{M} \mathbf{u}_{n} $$ In this example we apply the boundary conditions to the assembled discrete operators (mass matrix $\mathbf{M}$ and stiffnes matrix $\mathbf{K}$) only once. We utilize the fact that in finite element computations Dirichlet conditions can be applied by zero out rows and columns that correspond to a prescribed dof in the system matrix ($\mathbf{A} = Δt \mathbf{K} + \mathbf{M}$) and setting the value of the right-hand side vector to the value of the Dirichlet condition. Thus, we only need to apply in every time step the Dirichlet condition to the right-hand side of the problem.

Commented program¶

Now we solve the problem in Ferrite. What follows is a program spliced with comments.

First we load Ferrite, and some other packages we need.

In [1]:

using Ferrite, SparseArrays, WriteVTK

We create the same grid as in the heat equation example.

In [2]:

grid = generate_grid(Quadrilateral, (100, 100));

Trial and test functions¶

Again, we define the structs that are responsible for the shape_value and shape_gradient evaluation.

In [3]:

ip = Lagrange{RefQuadrilateral, 1}()
qr = QuadratureRule{RefQuadrilateral}(2)
cellvalues = CellValues(qr, ip);

Degrees of freedom¶

After this, we can define the DofHandler and distribute the DOFs of the problem.

In [4]:

dh = DofHandler(grid)
add!(dh, :u, ip)
close!(dh);

By means of the DofHandler we can allocate the needed SparseMatrixCSC. M refers here to the so called mass matrix, which always occurs in time related terms, i.e. $$ M_{ij} = \int_{\Omega} v_i \, u_j \ \mathrm{d}\Omega, $$ where $u_i$ and $v_j$ are trial and test functions, respectively.

In [5]:

K = allocate_matrix(dh);
M = allocate_matrix(dh);

We also preallocate the right hand side

In [6]:

f = zeros(ndofs(dh));

Boundary conditions¶

In order to define the time dependent problem, we need some end time T and something that describes the linearly increasing Dirichlet boundary condition on $\partial \Omega_2$.

In [7]:

max_temp = 100
Δt = 1
T = 200
t_rise = 100
ch = ConstraintHandler(dh);

Here, we define the boundary condition related to $\partial \Omega_1$.

In [8]:

∂Ω₁ = union(getfacetset.((grid,), ["left", "right"])...)
dbc = Dirichlet(:u, ∂Ω₁, (x, t) -> 0)
add!(ch, dbc);

While the next code block corresponds to the linearly increasing temperature description on $\partial \Omega_2$ until t=t_rise, and then keep constant

In [9]:

∂Ω₂ = union(getfacetset.((grid,), ["top", "bottom"])...)
dbc = Dirichlet(:u, ∂Ω₂, (x, t) -> max_temp * clamp(t / t_rise, 0, 1))
add!(ch, dbc)
close!(ch)
update!(ch, 0.0);

Assembling the linear system¶

As in the heat equation example we define a doassemble! function that assembles the diffusion parts of the equation:

In [10]:

function doassemble_K!(K::SparseMatrixCSC, f::Vector, cellvalues::CellValues, dh::DofHandler)

    n_basefuncs = getnbasefunctions(cellvalues)
    Ke = zeros(n_basefuncs, n_basefuncs)
    fe = zeros(n_basefuncs)

    assembler = start_assemble(K, f)

    for cell in CellIterator(dh)

        fill!(Ke, 0)
        fill!(fe, 0)

        reinit!(cellvalues, cell)

        for q_point in 1:getnquadpoints(cellvalues)
            dΩ = getdetJdV(cellvalues, q_point)

            for i in 1:n_basefuncs
                v = shape_value(cellvalues, q_point, i)
                ∇v = shape_gradient(cellvalues, q_point, i)
                fe[i] += 0.1 * v * dΩ
                for j in 1:n_basefuncs
                    ∇u = shape_gradient(cellvalues, q_point, j)
                    Ke[i, j] += 1.0e-3 * (∇v ⋅ ∇u) * dΩ
                end
            end
        end

        assemble!(assembler, celldofs(cell), Ke, fe)
    end
    return K, f
end

Out[10]:

doassemble_K! (generic function with 1 method)

In addition to the diffusive part, we also need a function that assembles the mass matrix M.

In [11]:

function doassemble_M!(M::SparseMatrixCSC, cellvalues::CellValues, dh::DofHandler)

    n_basefuncs = getnbasefunctions(cellvalues)
    Me = zeros(n_basefuncs, n_basefuncs)

    assembler = start_assemble(M)

    for cell in CellIterator(dh)

        fill!(Me, 0)

        reinit!(cellvalues, cell)

        for q_point in 1:getnquadpoints(cellvalues)
            dΩ = getdetJdV(cellvalues, q_point)

            for i in 1:n_basefuncs
                v = shape_value(cellvalues, q_point, i)
                for j in 1:n_basefuncs
                    u = shape_value(cellvalues, q_point, j)
                    Me[i, j] += (v * u) * dΩ
                end
            end
        end

        assemble!(assembler, celldofs(cell), Me)
    end
    return M
end

Out[11]:

doassemble_M! (generic function with 1 method)

Solution of the system¶

We first assemble all parts in the prior allocated SparseMatrixCSC.

In [12]:

K, f = doassemble_K!(K, f, cellvalues, dh)
M = doassemble_M!(M, cellvalues, dh)
A = (Δt .* K) + M;

Now, we need to save all boundary condition related values of the unaltered system matrix A, which is done by get_rhs_data. The function returns a RHSData struct, which contains all needed information to apply the boundary conditions solely on the right-hand-side vector of the problem.

In [13]:

rhsdata = get_rhs_data(ch, A);

We set the values at initial time step, denoted by uₙ, to a bubble-shape described by $(x_1^2-1)(x_2^2-1)$, such that it is zero at the boundaries and the maximum temperature in the center.

In [14]:

uₙ = zeros(length(f));
apply_analytical!(uₙ, dh, :u, x -> (x[1]^2 - 1) * (x[2]^2 - 1) * max_temp);

Here, we apply once the boundary conditions to the system matrix A.

In [15]:

apply!(A, ch);

To store the solution, we initialize a paraview collection (.pvd) file,

In [16]:

pvd = paraview_collection("transient-heat")
VTKGridFile("transient-heat-0", dh) do vtk
    write_solution(vtk, dh, uₙ)
    pvd[0.0] = vtk
end

Out[16]:

VTKGridFile for the closed file "transient-heat-0.vtu".

At this point everything is set up and we can finally approach the time loop.

In [17]:

for (step, t) in enumerate(Δt:Δt:T)
    #First of all, we need to update the Dirichlet boundary condition values.
    update!(ch, t)

    #Secondly, we compute the right-hand-side of the problem.
    b = Δt .* f .+ M * uₙ
    #Then, we can apply the boundary conditions of the current time step.
    apply_rhs!(rhsdata, b, ch)

    #Finally, we can solve the time step and save the solution afterwards.
    u = A \ b

    VTKGridFile("transient-heat-$step", dh) do vtk
        write_solution(vtk, dh, u)
        pvd[t] = vtk
    end
    #At the end of the time loop, we set the previous solution to the current one and go to the next time step.
    uₙ .= u
end

In order to use the .pvd file we need to store it to the disk, which is done by:

In [18]:

vtk_save(pvd);

This notebook was generated using Literate.jl.