ETHZ: 227-0966-00L¶

Quantitative Big Imaging¶

March 21, 2019¶

Supervised Approaches¶

Reading Material¶

Overview¶

Methods
Pipelines
Classification
Regression
Segmentation

In [1]:

import seaborn as sns
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (8, 8)
plt.rcParams["figure.dpi"] = 150
plt.rcParams["font.size"] = 14
plt.rcParams['font.family'] = ['sans-serif']
plt.rcParams['font.sans-serif'] = ['DejaVu Sans']
plt.style.use('ggplot')
sns.set_style("whitegrid", {'axes.grid': False})

Basic Methods Overview¶

There are a number of methods we can use for classification, regression and both. For the simplification of the material we will not make a massive distinction between classification and regression but there are many situations where this is not appropriate. Here we cover a few basic methods, since these are important to understand as a starting point for solving difficult problems. The list is not complete and importantly Support Vector Machines are completely missing which can be a very useful tool in supervised analysis. A core idea to supervised models is they have a training phase and a predicting phase.

Training¶

The training phase is when the parameters of the model are learned and involve putting inputs into the model and updating the parameters so they better match the outputs. This is a sort-of curve fitting (with linear regression it is exactly curve fitting).

Predicting¶

The predicting phase is once the parameters have been set applying the model to new datasets. At this point the parameters are no longer adjusted or updated and the model is frozen. Generally it is not possible to tweak a model any more using new data but some approaches (most notably neural networks) are able to handle this.

In [2]:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
%matplotlib inline

blob_data, blob_labels = make_blobs(n_samples=100,
                                    random_state=2018)
test_pts = pd.DataFrame(blob_data, columns=['x', 'y'])
test_pts['group_id'] = blob_labels
plt.scatter(test_pts.x, test_pts.y,
            c=test_pts.group_id,
            cmap='viridis')
test_pts.sample(5)

Out[2]:

	x	y	group_id
83	8.314519	-3.578486	1
91	8.081294	-4.805754	1
97	8.212069	-5.487216	1
46	8.869062	-1.978022	1
22	-1.227507	1.605207	2

Nearest Neighbor (or K Nearest Neighbors)¶

The technique is as basic as it sounds, it basically finds the nearest point to what you have put in.

In [3]:

from sklearn.neighbors import KNeighborsClassifier
import numpy as np
k_class = KNeighborsClassifier(1)
k_class.fit(X=np.reshape([0, 1, 2, 3], (-1, 1)),
            y=['I', 'am', 'a', 'dog'])

Out[3]:

KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=None, n_neighbors=1, p=2,
           weights='uniform')

In [4]:

print(k_class.predict(np.reshape([0, 1, 2, 3],
                                 (-1, 1))))

['I' 'am' 'a' 'dog']

In [5]:

print(k_class.predict(np.reshape([1.5], (1, 1))))
print(k_class.predict(np.reshape([100], (1, 1))))

['am']
['dog']

In [6]:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
%matplotlib inline

blob_data, blob_labels = make_blobs(n_samples=100,
                                    cluster_std=2.0,
                                    random_state=2018)
test_pts = pd.DataFrame(blob_data, columns=['x', 'y'])
test_pts['group_id'] = blob_labels
plt.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')
test_pts.sample(5)

Out[6]:

	x	y	group_id
7	8.225316	-5.347979	0
43	0.232685	1.511680	2
75	11.048954	-6.963938	1
0	8.964347	-2.898709	1
31	10.108296	-5.760553	0

In [7]:

k_class = KNeighborsClassifier(1)
k_class.fit(test_pts[['x', 'y']], test_pts['group_id']) 

Out[7]:

KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
           metric_params=None, n_jobs=None, n_neighbors=1, p=2,
           weights='uniform')

In [8]:

xx, yy = np.meshgrid(np.linspace(test_pts.x.min(), test_pts.x.max(), 30),
                     np.linspace(test_pts.y.min(), test_pts.y.max(), 30),
                     indexing='ij'
                     )
grid_pts = pd.DataFrame(dict(x=xx.ravel(), y=yy.ravel()))
grid_pts['predicted_id'] = k_class.predict(grid_pts[['x', 'y']])

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')
ax1.set_title('Training Data')
ax2.scatter(grid_pts.x, grid_pts.y, c=grid_pts.predicted_id, cmap='viridis')
ax2.set_title('Testing Points')

Out[8]:

Text(0.5, 1.0, 'Testing Points')

Stabilizing Results¶

We can see here that the result is thrown off by single points, we can improve by using more than the nearest neighbor and include the average of the nearest 2 neighbors

In [9]:

k_class = KNeighborsClassifier(4)
k_class.fit(test_pts[['x', 'y']], test_pts['group_id'])
xx, yy = np.meshgrid(np.linspace(test_pts.x.min(), test_pts.x.max(), 30),
                     np.linspace(test_pts.y.min(), test_pts.y.max(), 30),
                     indexing='ij'
                     )
grid_pts = pd.DataFrame(dict(x=xx.ravel(), y=yy.ravel()))
grid_pts['predicted_id'] = k_class.predict(grid_pts[['x', 'y']])

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')
ax1.set_title('Training Data')
ax2.scatter(grid_pts.x, grid_pts.y, c=grid_pts.predicted_id, cmap='viridis')
ax2.set_title('Testing Points')

Out[9]:

Text(0.5, 1.0, 'Testing Points')

Linear Regression¶

Linear regression is a fancy-name for linear curve fitting, fitting a line through points (sometimes in more than one dimension). It is a very basic method, but is easy to understand, interpret and fast to compute

In [10]:

from sklearn.linear_model import LinearRegression
import numpy as np
l_reg = LinearRegression()
l_reg.fit(X=np.reshape([0, 1, 2, 3], (-1, 1)),
          y=[10, 20, 30, 40])
l_reg.coef_, l_reg.intercept_

Out[10]:

(array([10.]), 10.0)

In [11]:

print(l_reg.predict(np.reshape([0, 1, 2, 3], (-1, 1))))
print(-100, '->', l_reg.predict(np.reshape([-100], (1, 1))))
print(500, '->', l_reg.predict(np.reshape([500], (1, 1))))

[10. 20. 30. 40.]
100 -> [-990.]
500 -> [5010.]

In [12]:

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

import numpy as np
import pandas as pd
blob_data, blob_labels = make_blobs(centers=2, n_samples=100,
                                    random_state=2018)
test_pts = pd.DataFrame(blob_data, columns=['x', 'y'])
test_pts['group_id'] = blob_labels
plt.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')
test_pts.sample(5)

Out[12]:

	x	y	group_id
95	7.604290	-6.575529	0
71	9.795385	-9.192932	0
53	8.529693	-3.438141	1
12	8.790663	-4.302533	1
21	7.593108	-6.840649	0

In [13]:

l_reg = LinearRegression()
l_reg.fit(test_pts[['x', 'y']], test_pts['group_id'])
print('Slope', l_reg.coef_)
print('Offset', l_reg.intercept_)

Slope [0.04813137 0.20391973]
Offset 1.346929708594462

In [14]:

xx, yy = np.meshgrid(np.linspace(test_pts.x.min(), test_pts.x.max(), 20),
                     np.linspace(test_pts.y.min(), test_pts.y.max(), 20),
                     indexing='ij'
                     )
grid_pts = pd.DataFrame(dict(x=xx.ravel(), y=yy.ravel()))
grid_pts['predicted_id'] = l_reg.predict(grid_pts[['x', 'y']])

fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(12, 4))
ax1.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')
ax1.set_title('Training Data')
ax2.scatter(grid_pts.x, grid_pts.y, c=grid_pts.predicted_id, cmap='viridis')
ax2.set_title('Testing Points')
ax3.imshow(grid_pts.predicted_id.values.reshape(
    xx.shape).T[::-1], cmap='viridis')
ax3.set_title('Test Image')

Out[14]:

Text(0.5, 1.0, 'Test Image')

Trees¶

In [15]:

from sklearn.tree import export_graphviz
import graphviz


def show_tree(in_tree):
    return graphviz.Source(export_graphviz(in_tree, out_file=None))

In [16]:

from sklearn.tree import DecisionTreeClassifier
import numpy as np
d_tree = DecisionTreeClassifier()
d_tree.fit(X=np.reshape([0, 1, 2, 3], (-1, 1)),
           y=[0, 1, 0, 1])

Out[16]:

DecisionTreeClassifier(class_weight=None, criterion='gini', max_depth=None,
            max_features=None, max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, presort=False, random_state=None,
            splitter='best')

In [17]:

show_tree(d_tree)

Out[17]:

In [18]:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
%matplotlib inline

blob_data, blob_labels = make_blobs(n_samples=100,
                                    random_state=2018)
test_pts = pd.DataFrame(blob_data, columns=['x', 'y'])
test_pts['group_id'] = blob_labels
plt.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')
test_pts.sample(5)

Out[18]:

	x	y	group_id
5	-1.648928	0.641026	2
77	-0.435923	-0.820777	2
87	9.447950	-4.622582	1
24	-0.826957	2.629860	2
57	7.370485	-8.489127	0

In [19]:

d_tree = DecisionTreeClassifier()
d_tree.fit(test_pts[['x', 'y']],
           test_pts['group_id'])
show_tree(d_tree)

Out[19]:

In [20]:

xx, yy = np.meshgrid(np.linspace(test_pts.x.min(), test_pts.x.max(), 20),
                     np.linspace(test_pts.y.min(), test_pts.y.max(), 20),
                     indexing='ij'
                     )
grid_pts = pd.DataFrame(dict(x=xx.ravel(), y=yy.ravel()))
grid_pts['predicted_id'] = d_tree.predict(grid_pts[['x', 'y']])

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 4))
ax1.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')
ax1.set_title('Training Data')
ax2.scatter(grid_pts.x, grid_pts.y, c=grid_pts.predicted_id, cmap='viridis')
ax2.set_title('Testing Points')

Out[20]:

Text(0.5, 1.0, 'Testing Points')

Forests¶

Forests are basically the idea of taking a number of trees and bringing them together. So rather than taking a single tree to do the classification, you divide the samples and the features to make different trees and then combine the results. One of the more successful approaches is called Random Forests or as a video

In [84]:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
%matplotlib inline

blob_data, blob_labels = make_blobs(n_samples=1000,
                                    cluster_std=3,
                                    random_state=2018)
test_pts = pd.DataFrame(blob_data, columns=['x', 'y'])
test_pts['group_id'] = blob_labels
plt.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')

Out[84]:

<matplotlib.collections.PathCollection at 0x12793cb38>

In [85]:

from sklearn.ensemble import RandomForestClassifier
rf_class = RandomForestClassifier(n_estimators=5, random_state=2018)
rf_class.fit(test_pts[['x', 'y']],
             test_pts['group_id'])
print('Build ', len(rf_class.estimators_), 'decision trees')

Build  5 decision trees

In [86]:

show_tree(rf_class.estimators_[0])

Out[86]:

In [24]:

show_tree(rf_class.estimators_[1])

Out[24]:

In [87]:

xx, yy = np.meshgrid(np.linspace(test_pts.x.min(), test_pts.x.max(), 20),
                     np.linspace(test_pts.y.min(), test_pts.y.max(), 20),
                     indexing='ij'
                     )
grid_pts = pd.DataFrame(dict(x=xx.ravel(), y=yy.ravel()))

fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(14, 3), dpi=150)
ax1.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')
ax1.set_title('Training Data')
ax2.scatter(grid_pts.x, grid_pts.y, c=rf_class.predict(
    grid_pts[['x', 'y']]), cmap='viridis')
ax2.set_title('Random Forest Classifier')

ax3.scatter(grid_pts.x, grid_pts.y, c=rf_class.estimators_[
            0].predict(grid_pts[['x', 'y']]), cmap='viridis')
ax3.set_title('First Decision Tree')

ax4.scatter(grid_pts.x, grid_pts.y, c=rf_class.estimators_[
            1].predict(grid_pts[['x', 'y']]), cmap='viridis')
ax4.set_title('Second Decision Tree')

Out[87]:

Text(0.5, 1.0, 'Second Decision Tree')

Pipelines¶

We will use the idea of pipelines generically here to refer to the combination of steps that need to be performed to solve a problem.

In [26]:

%%file pipe_utils.py
from sklearn.preprocessing import FunctionTransformer
import numpy as np
from skimage.filters import laplace, gaussian, median
from skimage.util import montage as montage2d
import matplotlib.pyplot as plt



def display_data(in_ax, raw_data, show_hist):
    if (raw_data.shape[0] == 1) and (len(raw_data.shape) == 4):
        # reformat channels first
        in_data = raw_data[0].swapaxes(0, 2).swapaxes(1, 2)
    else:
        in_data = np.squeeze(raw_data)
    if len(in_data.shape) == 1:
        if show_hist:
            in_ax.hist(in_data)
        else:
            in_ax.plot(in_data, 'r.')
    elif len(in_data.shape) == 2:
        if show_hist:
            for i in range(in_data.shape[1]):
                in_ax.hist(in_data[:, i], label='Dim:{}'.format(i), alpha=0.5)
            in_ax.legend()
        else:
            if in_data.shape[1] == 2:
                in_ax.plot(in_data[:, 0], in_data[:, 1], 'r.')
            else:
                in_ax.plot(in_data, '.')
    elif len(in_data.shape) == 3:
        if show_hist:
            in_ax.hist(in_data.ravel())
        else:
            n_stack = np.stack([(x-x.mean())/x.std() for x in in_data], 0)
            in_ax.imshow(montage2d(n_stack))


def show_pipe(pipe, in_data, show_hist=False):
    m_rows = np.ceil((len(pipe.steps)+1)/3).astype(int)
    fig, t_axs = plt.subplots(m_rows, 3, figsize=(12, 5*m_rows))
    m_axs = t_axs.flatten()
    [c_ax.axis('off') for c_ax in m_axs]
    last_data = in_data
    for i, (c_ax, (step_name, step_op)) in enumerate(zip(m_axs, [('Input Data', None)]+pipe.steps), 1):
        if step_op is not None:
            try:
                last_data = step_op.transform(last_data)
            except AttributeError:
                try:
                    last_data = step_op.predict_proba(last_data)
                except AttributeError:
                    last_data = step_op.predict(last_data)

        display_data(c_ax, last_data, show_hist)
        c_ax.set_title('Step {} {}\n{}'.format(i, last_data.shape, step_name))
        c_ax.axis('on')


def flatten_func(x): return np.reshape(x, (np.shape(x)[0], -1))


flatten_step = FunctionTransformer(flatten_func, validate=False)


def px_flatten_func(in_x):
    if len(in_x.shape) == 2:
        x = np.expand_dims(in_x, -1)
    elif len(in_x.shape) == 3:
        x = in_x
    elif len(in_x.shape) == 4:
        x = in_x
    else:
        raise ValueError(
            'Cannot work with images with dimensions {}'.format(in_x.shape))
    return np.reshape(x, (-1, np.shape(x)[-1]))


px_flatten_step = FunctionTransformer(px_flatten_func, validate=False)


def add_filters(in_x, filt_func=[lambda x: gaussian(x, sigma=2),
                                 lambda x: gaussian(
                                     x, sigma=5)-gaussian(x, sigma=2),
                                 lambda x: gaussian(x, sigma=8)-gaussian(x, sigma=5)]):
    if len(in_x.shape) == 2:
        x = np.expand_dims(np.expand_dims(in_x, 0), -1)
    elif len(in_x.shape) == 3:
        x = np.expand_dims(in_x, -1)
    elif len(in_x.shape) == 4:
        x = in_x
    else:
        raise ValueError(
            'Cannot work with images with dimensions {}'.format(in_x.shape))
    n_img, x_dim, y_dim, c_dim = x.shape
    out_imgs = [x]
    for c_filt in filt_func:
        out_imgs += [np.stack([np.stack([c_filt(x[i, :, :, j])
                                         for i in range(n_img)], 0)
                               for j in range(c_dim)], -1)]

    return np.concatenate(out_imgs, -1)


filter_step = FunctionTransformer(add_filters, validate=False)


def add_xy_coord(in_x, polar=False):
    if len(in_x.shape) == 2:
        x = np.expand_dims(np.expand_dims(in_x, 0), -1)
    elif len(in_x.shape) == 3:
        x = np.expand_dims(in_x, -1)
    elif len(in_x.shape) == 4:
        x = in_x
    else:
        raise ValueError(
            'Cannot work with images with dimensions {}'.format(in_x.shape))
    n_img, x_dim, y_dim, c_dim = x.shape

    _, xx, yy, _ = np.meshgrid(np.arange(n_img),
                               np.arange(x_dim),
                               np.arange(y_dim),
                               [1],
                               indexing='ij')
    if polar:
        rr = np.sqrt(np.square(xx-xx.mean())+np.square(yy-yy.mean()))
        th = np.arctan2(yy-yy.mean(), xx-xx.mean())
        return np.concatenate([x, rr, th], -1)
    else:
        return np.concatenate([x, xx, yy], -1)


xy_step = FunctionTransformer(add_xy_coord, validate=False)
polar_step = FunctionTransformer(
    lambda x: add_xy_coord(x, polar=True), validate=False)


def fit_img_pipe(in_pipe, in_x, in_y):
    in_pipe.fit(in_x,
                px_flatten_func(in_y)[:, 0])

    def predict_func(new_x):
        x_dim, y_dim = new_x.shape[0:2]
        return in_pipe.predict(new_x).reshape((x_dim, y_dim, -1))
    return predict_func

Overwriting pipe_utils.py

In [27]:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
%matplotlib inline


blob_data, blob_labels = make_blobs(n_samples=100,
                                    random_state=2018)
test_pts = pd.DataFrame(blob_data, columns=['x', 'y'])
test_pts['group_id'] = blob_labels

plt.scatter(test_pts.x, test_pts.y, c=test_pts.group_id, cmap='viridis')
test_pts.sample(5)

Out[27]:

	x	y	group_id
32	7.041214	-8.061979	0
51	6.436361	-8.220122	0
50	-1.377566	2.288469	2
4	8.922199	-3.463288	1
43	-0.419569	1.655694	2

In [28]:

from pipe_utils import show_pipe
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import RobustScaler
simple_pipe = Pipeline([('Normalize', RobustScaler())])
simple_pipe.fit(test_pts)

show_pipe(simple_pipe, test_pts.values)
show_pipe(simple_pipe, test_pts.values, show_hist=True)

In [29]:

from sklearn.preprocessing import QuantileTransformer
longer_pipe = Pipeline([('Quantile', QuantileTransformer(2)),
                        ('Normalize', RobustScaler())
                        ])
longer_pipe.fit(test_pts)

show_pipe(longer_pipe, test_pts.values)
show_pipe(longer_pipe, test_pts.values, show_hist=True)

In [30]:

from sklearn.preprocessing import PolynomialFeatures
messy_pipe = Pipeline([
    ('Normalize', RobustScaler()),
    ('PolynomialFeatures', PolynomialFeatures(2)),
])
messy_pipe.fit(test_pts)

show_pipe(messy_pipe, test_pts.values)
show_pipe(messy_pipe, test_pts.values, show_hist=True)

Classification¶

A common problem of putting images into categories. The standard problem for this is classifying digits between 0 and 9. Fundamentally a classification problem is one where we are taking a large input (images, vectors, ...) and trying to put it into a category.

In [31]:

from sklearn.datasets import load_digits
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs 
from pipe_utils import show_pipe
%matplotlib inline
digit_ds = load_digits(return_X_y=False)
img_data = digit_ds.images[:50]
digit_id = digit_ds.target[:50]
print('Image Data', img_data.shape)

Image Data (50, 8, 8)

In [32]:

from pipe_utils import flatten_step
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import RobustScaler
digit_pipe = Pipeline([('Flatten', flatten_step),
                       ('Normalize', RobustScaler())])
digit_pipe.fit(img_data)

show_pipe(digit_pipe, img_data)
show_pipe(digit_pipe, img_data, show_hist=True)

In [33]:

from sklearn.neighbors import KNeighborsClassifier

digit_class_pipe = Pipeline([('Flatten', flatten_step),
                             ('Normalize', RobustScaler()),
                             ('NearestNeighbor', KNeighborsClassifier(1))])
digit_class_pipe.fit(img_data, digit_id)

show_pipe(digit_class_pipe, img_data)

In [34]:

from sklearn.metrics import accuracy_score
pred_digit = digit_class_pipe.predict(img_data)
print('%2.2f%% accuracy' % (100*accuracy_score(digit_id, pred_digit)))

100.00% accuracy

In [35]:

from sklearn.metrics import confusion_matrix
import seaborn as sns
fig, ax1 = plt.subplots(1, 1, figsize=(8, 8), dpi=120)
sns.heatmap(
    confusion_matrix(digit_id, pred_digit),
    annot=True,
    fmt='d',
    ax=ax1)

Out[35]:

<matplotlib.axes._subplots.AxesSubplot at 0x1195b8b38>

In [36]:

from sklearn.metrics import classification_report
print(classification_report(digit_id, pred_digit))

              precision    recall  f1-score   support

           0       1.00      1.00      1.00         7
           1       1.00      1.00      1.00         5
           2       1.00      1.00      1.00         3
           3       1.00      1.00      1.00         4
           4       1.00      1.00      1.00         4
           5       1.00      1.00      1.00         7
           6       1.00      1.00      1.00         4
           7       1.00      1.00      1.00         5
           8       1.00      1.00      1.00         5
           9       1.00      1.00      1.00         6

   micro avg       1.00      1.00      1.00        50
   macro avg       1.00      1.00      1.00        50
weighted avg       1.00      1.00      1.00        50

Wow! We've built an amazing algorithm!¶

Let's patent it! Call Google!¶

In [37]:

test_digit = np.array([[[0.,  0.,  6., 12., 13.,  6.,  0.,  0.],
                        [0.,  6., 16.,  9., 12., 16.,  2.,  0.],
                        [0.,  7., 16.,  9., 15., 13.,  0.,  0.],
                        [0.,  0., 11., 15., 16.,  4.,  0.,  0.],
                        [0.,  0.,  0., 12., 10.,  0.,  0.,  0.],
                        [0.,  0.,  3., 16.,  4.,  0.,  0.,  0.],
                        [0.,  0.,  1., 16.,  2.,  0.,  0.,  0.],
                        [0.,  0.,  6., 11.,  0.,  0.,  0.,  0.]]])
plt.matshow(test_digit[0], cmap='bone')
print('Prediction:', digit_class_pipe.predict(test_digit))
print('Real Value:', 9)

Prediction: [7]
Real Value: 9

Training, Validation, and Testing¶

https://www.kdnuggets.com/2017/08/dataiku-predictive-model-holdout-cross-validation.html

Regression¶

For regression, we can see it very similarly to a classification but instead of trying to output discrete classes we can output on a continuous scale. So we can take the exact same task (digits) but instead of predicting the category we can predict the actual decimal number

In [38]:

from sklearn.datasets import load_digits
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from pipe_utils import show_pipe, flatten_step
%matplotlib inline
digit_ds = load_digits(return_X_y=False)

img_data = digit_ds.images[:50]
digit_id = digit_ds.target[:50]

valid_data = digit_ds.images[50:500]
valid_id = digit_ds.target[50:500]

In [39]:

from sklearn.neighbors import KNeighborsRegressor

digit_regress_pipe = Pipeline([('Flatten', flatten_step),
                               ('Normalize', RobustScaler()),
                               ('NearestNeighbor', KNeighborsRegressor(1))])
digit_regress_pipe.fit(img_data, digit_id)

show_pipe(digit_regress_pipe, img_data)

Assessment¶

We can't use accuracy, ROC, precision, recall or any of these factors anymore since we don't have binary / true-or-false conditions we are trying to predict. We know have to go back to some of the initial metrics we covered in the first lectures.

$$ MSE = \frac{1}{N}\sum \left(y_{predicted} - y_{actual}\right)^2 $$$$ MAE = \frac{1}{N}\sum |y_{predicted} - y_{actual}| $$

In [40]:

import seaborn as sns
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6), dpi=200)
pred_train = digit_regress_pipe.predict(img_data)
jitter = lambda x: x+0.25*np.random.uniform(-1, 1, size=x.shape)
sns.swarmplot(digit_id, jitter(pred_train), ax=ax1)
ax1.set_title('Predictions (Training)\nMSE: %2.2f MAE: %2.2f' % (np.mean(np.square(pred_train-digit_id)),
                                                                 np.mean(np.abs(pred_train-digit_id))))

pred_valid = digit_regress_pipe.predict(valid_data)
sns.swarmplot(valid_id, jitter(pred_valid), ax=ax2)
ax2.set_title('Predictions (Validation)\nMSE: %2.2f MAE: %2.2f' % (np.mean(np.square(pred_valid-valid_id)),
                                                                   np.mean(np.abs(pred_valid-valid_id))))

Out[40]:

Text(0.5, 1.0, 'Predictions (Validation)\nMSE: 7.71 MAE: 1.41')

Increasing neighbor count¶

In [41]:

digit_regress_pipe = Pipeline([('Flatten', flatten_step),
                               ('Normalize', RobustScaler()),
                               ('NearestNeighbor', KNeighborsRegressor(2))])
digit_regress_pipe.fit(img_data, digit_id)

show_pipe(digit_regress_pipe, img_data)

In [42]:

import seaborn as sns
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 6), dpi=200)
pred_train = digit_regress_pipe.predict(img_data)

sns.swarmplot(digit_id, jitter(pred_train), ax=ax1)
ax1.set_title('Predictions (Training)\nMSE: %2.2f MAE: %2.2f' % (np.mean(np.square(pred_train-digit_id)),
                                                                 np.mean(np.abs(pred_train-digit_id))))

pred_valid = digit_regress_pipe.predict(valid_data)
sns.swarmplot(valid_id, jitter(pred_valid), ax=ax2)
ax2.set_title('Predictions (Validation)\nMSE: %2.2f MAE: %2.2f' % (np.mean(np.square(pred_valid-valid_id)),
                                                                   np.mean(np.abs(pred_valid-valid_id))))

Out[42]:

Text(0.5, 1.0, 'Predictions (Validation)\nMSE: 6.07 MAE: 1.65')

Segmentation (Pixel Classification)¶

The first tasks we had were from one entire image to a single class (classification) or value (regression). Now we want to change problem, instead of a single class for each image, we want a class or value for each pixel. This requires that we restructure the problem.

Where segmentation fails: Mitochondria Segmentation in EM¶

Cortex Image

The cortex is barely visible to the human eye
Tiny structures hint at where cortex is located

A simple threshold is insufficient to finding the cortical structures
Other filtering techniques are unlikely to magicially fix this problem

In [43]:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from skimage.io import imread
%matplotlib inline
cell_img = (imread("../common/data/em_image.png")[::2, ::2])/255.0
cell_seg = imread("../common/data/em_image_seg.png",
                  as_gray=True)[::2, ::2] > 0
print(cell_img.shape, cell_seg.shape)
np.random.seed(2018)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 8), dpi=72)
ax1.imshow(cell_img, cmap='bone')
ax2.imshow(cell_seg, cmap='bone')

(384, 512) (384, 512)

Out[43]:

<matplotlib.image.AxesImage at 0x118339a20>

In [44]:

train_img, valid_img = cell_img[:, :256], cell_img[:, 256:]
train_mask, valid_mask = cell_seg[:, :256], cell_seg[:, 256:]
print('Training', train_img.shape, train_mask.shape)
print('Validation Data', valid_img.shape, valid_mask.shape)

Training (384, 256) (384, 256)
Validation Data (384, 256) (384, 256)

In [45]:

fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(8, 8), dpi=72)
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')
ax2.imshow(train_mask, cmap='bone')
ax2.set_title('Train Mask')

ax3.imshow(valid_img, cmap='bone')
ax3.set_title('Validation Image')
ax4.imshow(valid_mask, cmap='bone')
ax4.set_title('Validation Mask')

Out[45]:

Text(0.5, 1.0, 'Validation Mask')

In [46]:

from pipe_utils import px_flatten_step, show_pipe, fit_img_pipe
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import RobustScaler
from sklearn.cluster import KMeans
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor

rf_seg_model = Pipeline([('Pixel Flatten', px_flatten_step),
                         ('Robust Scaling', RobustScaler()),
                         ('Decision Tree', DecisionTreeRegressor())
                         ])

pred_func = fit_img_pipe(rf_seg_model, train_img, train_mask)
show_pipe(rf_seg_model, train_img)
show_tree(rf_seg_model.steps[-1][1])

Out[46]:

In [47]:

fig, ((ax1, ax5, ax2), (ax3, ax6, ax4)) = plt.subplots(
    2, 3, figsize=(12, 8), dpi=72)
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')

ax5.imshow(train_mask, cmap='viridis')
ax5.set_title('Train Mask')

ax2.imshow(pred_func(train_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax2.set_title('Prediction Mask')

ax3.imshow(cell_img, cmap='bone')
ax3.set_title('Full Image')

ax6.imshow(cell_seg, cmap='viridis')
ax6.set_title('Full Mask')

ax4.imshow(pred_func(cell_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Prediction Mask')

Out[47]:

Text(0.5, 1.0, 'Prediction Mask')

Include Position Information¶

In [48]:

from pipe_utils import xy_step

rf_xyseg_model = Pipeline([('Add XY', xy_step),
                           ('Pixel Flatten', px_flatten_step),
                           ('Normalize', RobustScaler()),
                           ('DecisionTree', DecisionTreeRegressor(
                               min_samples_split=1000))
                           ])

pred_func = fit_img_pipe(rf_xyseg_model, train_img, train_mask)
show_pipe(rf_xyseg_model, train_img)
show_tree(rf_xyseg_model.steps[-1][1])

Out[48]:

In [49]:

fig, ((ax1, ax5, ax2), (ax3, ax6, ax4)) = plt.subplots(
    2, 3, figsize=(12, 8), dpi=72)
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')

ax5.imshow(train_mask, cmap='viridis')
ax5.set_title('Train Mask')

ax2.imshow(pred_func(train_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax2.set_title('Prediction Mask')

ax3.imshow(cell_img, cmap='bone')
ax3.set_title('Full Image')

ax6.imshow(cell_seg, cmap='viridis')
ax6.set_title('Full Mask')

ax4.imshow(pred_func(cell_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Prediction Mask')

Out[49]:

Text(0.5, 1.0, 'Prediction Mask')

In [50]:

from sklearn.cluster import KMeans
rf_xyseg_k_model = Pipeline([('Add XY', xy_step),
                             ('Pixel Flatten', px_flatten_step),
                             ('Normalize', RobustScaler()),
                             ('KMeans', KMeans(4)),
                             ('RandomForest', RandomForestRegressor(n_estimators=25))
                             ])

pred_func = fit_img_pipe(rf_xyseg_k_model, train_img, train_mask)
show_pipe(rf_xyseg_k_model, train_img)

In [51]:

fig, ((ax1, ax5, ax2), (ax3, ax6, ax4)) = plt.subplots(
    2, 3, figsize=(12, 8), dpi=72)
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')

ax5.imshow(train_mask, cmap='viridis')
ax5.set_title('Train Mask')

ax2.imshow(pred_func(train_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax2.set_title('Prediction Mask')

ax3.imshow(cell_img, cmap='bone')
ax3.set_title('Full Image')

ax6.imshow(cell_seg, cmap='viridis')
ax6.set_title('Full Mask')

ax4.imshow(pred_func(cell_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Prediction Mask')

Out[51]:

Text(0.5, 1.0, 'Prediction Mask')

In [52]:

from sklearn.preprocessing import PolynomialFeatures
rf_xyseg_py_model = Pipeline([('Add XY', xy_step),
                              ('Pixel Flatten', px_flatten_step),
                              ('Normalize', RobustScaler()),
                              ('Polynomial Features', PolynomialFeatures(2)),
                              ('RandomForest', RandomForestRegressor(n_estimators=25))
                              ])

pred_func = fit_img_pipe(rf_xyseg_py_model, train_img, train_mask)
show_pipe(rf_xyseg_py_model, train_img)

In [53]:

fig, ((ax1, ax5, ax2), (ax3, ax6, ax4)) = plt.subplots(
    2, 3, figsize=(12, 8), dpi=72)
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')

ax5.imshow(train_mask, cmap='viridis')
ax5.set_title('Train Mask')

ax2.imshow(pred_func(train_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax2.set_title('Prediction Mask')

ax3.imshow(cell_img, cmap='bone')
ax3.set_title('Full Image')

ax6.imshow(cell_seg, cmap='viridis')
ax6.set_title('Full Mask')

ax4.imshow(pred_func(cell_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Prediction Mask')

Out[53]:

Text(0.5, 1.0, 'Prediction Mask')

Adding Smarter Features¶

Here we add images with filters and gaussians

In [54]:

from pipe_utils import filter_step
rf_filterseg_model = Pipeline([('Filters', filter_step),
                               ('Pixel Flatten', px_flatten_step),
                               ('Normalize', RobustScaler()),
                               ('RandomForest', RandomForestRegressor(n_estimators=25))
                               ])

pred_func = fit_img_pipe(rf_filterseg_model, train_img, train_mask)
show_pipe(rf_filterseg_model, train_img)

In [55]:

fig, ((ax1, ax5, ax2), (ax3, ax6, ax4)) = plt.subplots(
    2, 3, figsize=(12, 8), dpi=72)
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')

ax5.imshow(train_mask, cmap='viridis')
ax5.set_title('Train Mask')

ax2.imshow(pred_func(train_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax2.set_title('Prediction Mask')

ax3.imshow(cell_img, cmap='bone')
ax3.set_title('Full Image')

ax6.imshow(cell_seg, cmap='viridis')
ax6.set_title('Full Mask')

ax4.imshow(pred_func(cell_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Prediction Mask')

Out[55]:

Text(0.5, 1.0, 'Prediction Mask')

Using the Neighborhood¶

We can also include the whole neighborhood by shifting the image in x and y. For the first example we will then use linear regression so we can see the exact coefficients that result.

In [56]:

from sklearn.preprocessing import FunctionTransformer


def add_neighborhood(in_x, x_steps=3, y_steps=3):
    if len(in_x.shape) == 2:
        x = np.expand_dims(np.expand_dims(in_x, 0), -1)
    elif len(in_x.shape) == 3:
        x = np.expand_dims(in_x, -1)
    elif len(in_x.shape) == 4:
        x = in_x
    else:
        raise ValueError(
            'Cannot work with images with dimensions {}'.format(in_x.shape))
    n_img, x_dim, y_dim, c_dim = x.shape
    out_imgs = []
    for i in range(-x_steps, x_steps+1):
        for j in range(-y_steps, y_steps+1):
            out_imgs += [np.roll(np.roll(x,
                                         axis=1, shift=i),
                                 axis=2,
                                 shift=j)]
    return np.concatenate(out_imgs, -1)


def neighbor_step(x_steps=3, y_steps=3):
    return FunctionTransformer(
        lambda x: add_neighborhood(x, x_steps, y_steps),
        validate=False)

In [57]:

linreg_neighborseg_model = Pipeline([('Neighbors', neighbor_step(1, 1)),
                               ('Pixel Flatten', px_flatten_step),
                               ('Linear Regression', LinearRegression())
                               ])

pred_func = fit_img_pipe(linreg_neighborseg_model, train_img, train_mask)
show_pipe(linreg_neighborseg_model, train_img)

In [58]:

fig, ((ax1, ax5, ax2), (ax3, ax6, ax4)) = plt.subplots(
    2, 3, figsize=(12, 8), dpi=72)
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')

ax5.imshow(train_mask, cmap='viridis')
ax5.set_title('Train Mask')

ax2.imshow(pred_func(train_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax2.set_title('Prediction Mask')

ax3.imshow(cell_img, cmap='bone')
ax3.set_title('Full Image')

ax6.imshow(cell_seg, cmap='viridis')
ax6.set_title('Full Mask')

ax4.imshow(pred_func(cell_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Prediction Mask')

Out[58]:

Text(0.5, 1.0, 'Prediction Mask')

Why Linear Regression?¶

We choose linear regression so we could get easily understood coefficients. The model fits $\vec{m}$ and $b$ to the $\vec{x}_{i,j}$ points in the image $I(i,j)$ to match the $y_{i,j}$ output in the segmentation as closely as possible $$ y_{i,j} = \vec{m}\cdot\vec{x_{i,j}}+b $$ For a 3x3 cases this looks like $$ \vec{x}_{i,j} = \left[I(i-1,j-1), I(i-1, j), I(i-1, j+1) \dots I(i+1,j-1), I(i+1, j), I(i+1, j+1)\right] $$

In [59]:

m = linreg_neighborseg_model.steps[-1][1].coef_
b = linreg_neighborseg_model.steps[-1][1].intercept_
print('M:', m)
print('b:', b)

M: [-0.15008688 -0.052964   -0.14118507 -0.02355422  0.06656858 -0.04511923
 -0.10146375 -0.03607152 -0.18193311]
b: 0.42127748393139675

Convolution¶

The steps we have here make up a convolution and so what we have effectively done is use linear regression to learn which coefficients we should use in a convolutional kernel to get the best results

In [60]:

from scipy.ndimage import convolve
m_mat = m.reshape((3, 3)).T
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(16, 4))
sns.heatmap(m_mat,
            annot=True,
            ax=ax1, fmt='2.2f',
            vmin=-m_mat.std(),
            vmax=m_mat.std())
ax1.set_title(r'Kernel $\vec{m}$')
ax2.imshow(cell_img)
ax2.set_title('Input Image')
ax2.axis('off')

ax3.imshow(convolve(cell_img, m_mat)+b,
           vmin=0,
           vmax=1,
           cmap='viridis')
ax3.set_title('Post Convolution Image')
ax3.axis('off')

ax4.imshow(pred_func(cell_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Predicted from Linear Model')
ax4.axis('off')

Out[60]:

(-0.5, 511.5, 383.5, -0.5)

Nearest Neighbor¶

We can also use the neighborhood and nearest neighbor, this means for each pixel and its surrounds we find the pixel in the training set that looks most similar

In [61]:

nn_neighborseg_model = Pipeline([('Neighbors', neighbor_step(1, 1)),
                               ('Pixel Flatten', px_flatten_step),
                               ('Normalize', RobustScaler()),
                               ('NearestNeighbor', KNeighborsRegressor(n_neighbors=1))
                               ])

pred_func = fit_img_pipe(nn_neighborseg_model, train_img, train_mask)
show_pipe(nn_neighborseg_model, train_img)

In [62]:

fig, ((ax1, ax5, ax2), (ax3, ax6, ax4)) = plt.subplots(
    2, 3, figsize=(12, 8), dpi=72)
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')

ax5.imshow(train_mask, cmap='viridis')
ax5.set_title('Train Mask')

ax2.imshow(pred_func(train_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax2.set_title('Prediction Mask')

ax3.imshow(cell_img, cmap='bone')
ax3.set_title('Full Image')

ax6.imshow(cell_seg, cmap='viridis')
ax6.set_title('Full Mask')

ax4.imshow(pred_func(cell_img)[:, :, 0],
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Prediction Mask')

Out[62]:

Text(0.5, 1.0, 'Prediction Mask')

U-Net¶

The last approach we will briefly cover is the idea of U-Net a landmark paper from 2015 that dominates MICCAI submissions and contest winners today. A nice overview of the techniques is presented by Vladimir Iglovikov a winner of a recent Kaggle competition on masking images of cars slides

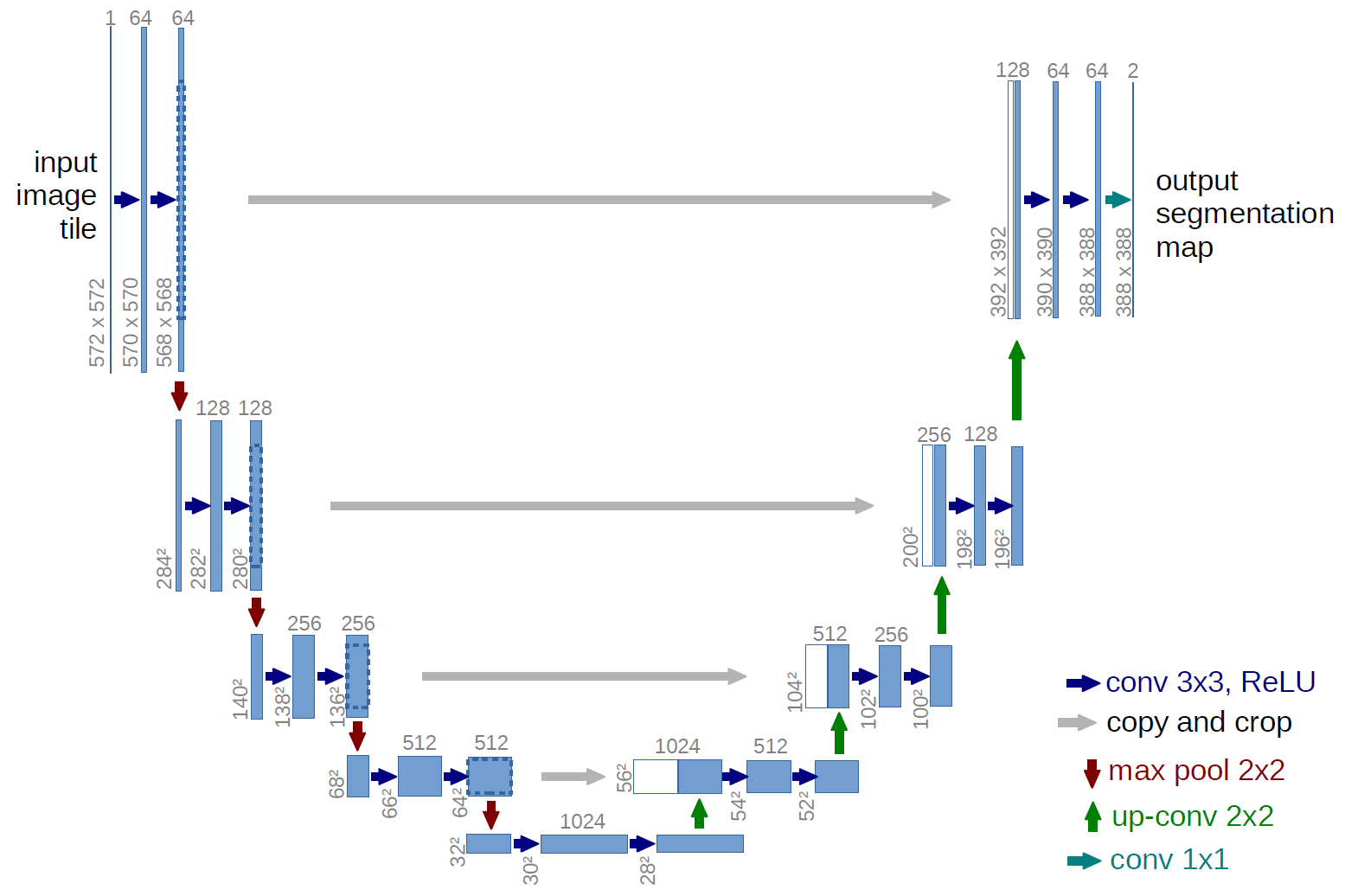
U-Net Diagram

In [63]:

from keras.models import Model
from keras.layers import Input, Conv2D, MaxPool2D, UpSampling2D, concatenate
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
base_depth = 32
in_img = Input((None, None, 1), name='Image_Input')
lay_1 = Conv2D(base_depth, kernel_size=(3, 3), padding='same')(in_img)
lay_2 = Conv2D(base_depth, kernel_size=(3, 3), padding='same')(lay_1)
lay_3 = MaxPool2D((2, 2))(lay_2)
lay_4 = Conv2D(base_depth*2, kernel_size=(3, 3), padding='same')(lay_3)
lay_5 = Conv2D(base_depth*2, kernel_size=(3, 3), padding='same')(lay_4)
lay_6 = MaxPool2D((2, 2))(lay_5)
lay_7 = Conv2D(base_depth*4, kernel_size=(3, 3), padding='same')(lay_6)
lay_8 = Conv2D(base_depth*4, kernel_size=(3, 3), padding='same')(lay_7)
lay_9 = UpSampling2D((2, 2))(lay_8)
lay_10 = concatenate([lay_5, lay_9])
lay_11 = Conv2D(base_depth*2, kernel_size=(3, 3), padding='same')(lay_10)
lay_12 = Conv2D(base_depth*2, kernel_size=(3, 3), padding='same')(lay_11)
lay_13 = UpSampling2D((2, 2))(lay_12)
lay_14 = concatenate([lay_2, lay_13])
lay_15 = Conv2D(base_depth, kernel_size=(3, 3), padding='same')(lay_14)
lay_16 = Conv2D(base_depth, kernel_size=(3, 3), padding='same')(lay_15)
lay_17 = Conv2D(1, kernel_size=(1, 1), padding='same',
                activation='sigmoid')(lay_16)
t_unet = Model(inputs=[in_img], outputs=[lay_17], name='SmallUNET')
dot_mod = model_to_dot(t_unet, show_shapes=True, show_layer_names=False)
dot_mod.set_rankdir('UD')
SVG(dot_mod.create_svg())

/anaconda3/envs/qbi2019/lib/python3.6/site-packages/h5py/__init__.py:36: FutureWarning: Conversion of the second argument of issubdtype from `float` to `np.floating` is deprecated. In future, it will be treated as `np.float64 == np.dtype(float).type`.
  from ._conv import register_converters as _register_converters
Using TensorFlow backend.

Out[63]:

In [64]:

t_unet.summary()

__________________________________________________________________________________________________
Layer (type)                    Output Shape         Param #     Connected to                     
==================================================================================================
Image_Input (InputLayer)        (None, None, None, 1 0                                            
__________________________________________________________________________________________________
conv2d_1 (Conv2D)               (None, None, None, 3 320         Image_Input[0][0]                
__________________________________________________________________________________________________
conv2d_2 (Conv2D)               (None, None, None, 3 9248        conv2d_1[0][0]                   
__________________________________________________________________________________________________
max_pooling2d_1 (MaxPooling2D)  (None, None, None, 3 0           conv2d_2[0][0]                   
__________________________________________________________________________________________________
conv2d_3 (Conv2D)               (None, None, None, 6 18496       max_pooling2d_1[0][0]            
__________________________________________________________________________________________________
conv2d_4 (Conv2D)               (None, None, None, 6 36928       conv2d_3[0][0]                   
__________________________________________________________________________________________________
max_pooling2d_2 (MaxPooling2D)  (None, None, None, 6 0           conv2d_4[0][0]                   
__________________________________________________________________________________________________
conv2d_5 (Conv2D)               (None, None, None, 1 73856       max_pooling2d_2[0][0]            
__________________________________________________________________________________________________
conv2d_6 (Conv2D)               (None, None, None, 1 147584      conv2d_5[0][0]                   
__________________________________________________________________________________________________
up_sampling2d_1 (UpSampling2D)  (None, None, None, 1 0           conv2d_6[0][0]                   
__________________________________________________________________________________________________
concatenate_1 (Concatenate)     (None, None, None, 1 0           conv2d_4[0][0]                   
                                                                 up_sampling2d_1[0][0]            
__________________________________________________________________________________________________
conv2d_7 (Conv2D)               (None, None, None, 6 110656      concatenate_1[0][0]              
__________________________________________________________________________________________________
conv2d_8 (Conv2D)               (None, None, None, 6 36928       conv2d_7[0][0]                   
__________________________________________________________________________________________________
up_sampling2d_2 (UpSampling2D)  (None, None, None, 6 0           conv2d_8[0][0]                   
__________________________________________________________________________________________________
concatenate_2 (Concatenate)     (None, None, None, 9 0           conv2d_2[0][0]                   
                                                                 up_sampling2d_2[0][0]            
__________________________________________________________________________________________________
conv2d_9 (Conv2D)               (None, None, None, 3 27680       concatenate_2[0][0]              
__________________________________________________________________________________________________
conv2d_10 (Conv2D)              (None, None, None, 3 9248        conv2d_9[0][0]                   
__________________________________________________________________________________________________
conv2d_11 (Conv2D)              (None, None, None, 1 33          conv2d_10[0][0]                  
==================================================================================================
Total params: 470,977
Trainable params: 470,977
Non-trainable params: 0
__________________________________________________________________________________________________

In [65]:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from skimage.io import imread
%matplotlib inline
cell_img = (imread("../common/data/em_image.png")[::2, ::2])/255.0
cell_seg = imread("../common/data/em_image_seg.png",
                  as_gray=True)[::2, ::2] > 0
train_img, valid_img = cell_img[:256, 50:250], cell_img[:, 256:]
train_mask, valid_mask = cell_seg[:256, 50:250], cell_seg[:, 256:]
# add channels and sample dimensions


def prep_img(x, n=1): return (
    prep_mask(x, n=n)-train_img.mean())/train_img.std()


def prep_mask(x, n=1): return np.stack([np.expand_dims(x, -1)]*n, 0)


print('Training', train_img.shape, train_mask.shape)
print('Validation Data', valid_img.shape, valid_mask.shape)
fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(2, 2, figsize=(8, 8), dpi=72)
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')
ax2.imshow(train_mask, cmap='bone')
ax2.set_title('Train Mask')

ax3.imshow(valid_img, cmap='bone')
ax3.set_title('Validation Image')
ax4.imshow(valid_mask, cmap='bone')
ax4.set_title('Validation Mask')

Training (256, 200) (256, 200)
Validation Data (384, 256) (384, 256)

Out[65]:

Text(0.5, 1.0, 'Validation Mask')

Results from Untrained Model¶

We can make predictions with an untrained model, but we clearly do not expect them to be very good

In [66]:

fig, m_axs = plt.subplots(2, 3,
                          figsize=(18, 8), dpi=150)
for c_ax in m_axs.flatten():
    c_ax.axis('off')
((ax1, ax2, _), (ax3, ax4, ax5)) = m_axs
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')
ax2.imshow(train_mask, cmap='viridis')
ax2.set_title('Train Mask')

ax3.imshow(cell_seg, cmap='bone')
ax3.set_title('Full Image')

unet_pred = t_unet.predict(prep_img(cell_img))[0, :, :, 0]
ax4.imshow(unet_pred,
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Predicted Segmentation')

ax5.imshow(cell_seg,
           cmap='viridis')
ax5.set_title('Ground Truth')

Out[66]:

Text(0.5, 1.0, 'Ground Truth')

Note¶

This is a very bad way to train a model, the loss function is poorly chosen, the optimizer can be improved the learning rate can be changed, the training and validation data should not come from the same sample (and definitely not the same measurement). The goal is to be aware of these techniques and have a feeling for how they can work for complex problems

In [67]:

from keras.optimizers import SGD
t_unet.compile(
    # we use a simple loss metric of mean-squared error to optimize
    loss='mse',
    # we use stochastic gradient descent to optimize
    optimizer=SGD(lr=0.05),
    # we keep track of the number of pixels correctly classified and the mean absolute error as well
    metrics=['binary_accuracy', 'mae']
)

loss_history = t_unet.fit(prep_img(train_img, n=5),
                          prep_mask(train_mask, n=5),
                          validation_data=(prep_img(valid_img),
                                           prep_mask(valid_mask)),
                          epochs=20)

Train on 5 samples, validate on 1 samples
Epoch 1/20
5/5 [==============================] - 5s 1s/step - loss: 0.3367 - binary_accuracy: 0.3617 - mean_absolute_error: 0.5602 - val_loss: 0.0945 - val_binary_accuracy: 0.8984 - val_mean_absolute_error: 0.2285
Epoch 2/20
5/5 [==============================] - 4s 898ms/step - loss: 0.1049 - binary_accuracy: 0.8878 - mean_absolute_error: 0.2428 - val_loss: 0.0763 - val_binary_accuracy: 0.8985 - val_mean_absolute_error: 0.1782
Epoch 3/20
5/5 [==============================] - 4s 867ms/step - loss: 0.0888 - binary_accuracy: 0.8879 - mean_absolute_error: 0.2074 - val_loss: 0.0673 - val_binary_accuracy: 0.8971 - val_mean_absolute_error: 0.1623
Epoch 4/20
5/5 [==============================] - 4s 700ms/step - loss: 0.0800 - binary_accuracy: 0.8867 - mean_absolute_error: 0.1979 - val_loss: 0.0616 - val_binary_accuracy: 0.9019 - val_mean_absolute_error: 0.1501
Epoch 5/20
5/5 [==============================] - 3s 620ms/step - loss: 0.0742 - binary_accuracy: 0.8901 - mean_absolute_error: 0.1885 - val_loss: 0.0586 - val_binary_accuracy: 0.9081 - val_mean_absolute_error: 0.1391
Epoch 6/20
5/5 [==============================] - 3s 603ms/step - loss: 0.0705 - binary_accuracy: 0.8989 - mean_absolute_error: 0.1771 - val_loss: 0.0570 - val_binary_accuracy: 0.9111 - val_mean_absolute_error: 0.1307
Epoch 7/20
5/5 [==============================] - 3s 601ms/step - loss: 0.0681 - binary_accuracy: 0.9041 - mean_absolute_error: 0.1672 - val_loss: 0.0560 - val_binary_accuracy: 0.9137 - val_mean_absolute_error: 0.1246
Epoch 8/20
5/5 [==============================] - 3s 578ms/step - loss: 0.0665 - binary_accuracy: 0.9074 - mean_absolute_error: 0.1596 - val_loss: 0.0555 - val_binary_accuracy: 0.9153 - val_mean_absolute_error: 0.1200
Epoch 9/20
5/5 [==============================] - 3s 586ms/step - loss: 0.0652 - binary_accuracy: 0.9094 - mean_absolute_error: 0.1535 - val_loss: 0.0551 - val_binary_accuracy: 0.9169 - val_mean_absolute_error: 0.1164
Epoch 10/20
5/5 [==============================] - 3s 630ms/step - loss: 0.0643 - binary_accuracy: 0.9109 - mean_absolute_error: 0.1485 - val_loss: 0.0549 - val_binary_accuracy: 0.9178 - val_mean_absolute_error: 0.1135
Epoch 11/20
5/5 [==============================] - 3s 661ms/step - loss: 0.0635 - binary_accuracy: 0.9126 - mean_absolute_error: 0.1445 - val_loss: 0.0548 - val_binary_accuracy: 0.9186 - val_mean_absolute_error: 0.1112
Epoch 12/20
5/5 [==============================] - 3s 663ms/step - loss: 0.0629 - binary_accuracy: 0.9138 - mean_absolute_error: 0.1411 - val_loss: 0.0548 - val_binary_accuracy: 0.9191 - val_mean_absolute_error: 0.1093
Epoch 13/20
5/5 [==============================] - 3s 640ms/step - loss: 0.0623 - binary_accuracy: 0.9150 - mean_absolute_error: 0.1382 - val_loss: 0.0547 - val_binary_accuracy: 0.9198 - val_mean_absolute_error: 0.1077
Epoch 14/20
5/5 [==============================] - 3s 629ms/step - loss: 0.0619 - binary_accuracy: 0.9158 - mean_absolute_error: 0.1356 - val_loss: 0.0548 - val_binary_accuracy: 0.9200 - val_mean_absolute_error: 0.1064
Epoch 15/20
5/5 [==============================] - 3s 635ms/step - loss: 0.0614 - binary_accuracy: 0.9163 - mean_absolute_error: 0.1334 - val_loss: 0.0548 - val_binary_accuracy: 0.9203 - val_mean_absolute_error: 0.1052
Epoch 16/20
5/5 [==============================] - 3s 611ms/step - loss: 0.0610 - binary_accuracy: 0.9171 - mean_absolute_error: 0.1315 - val_loss: 0.0549 - val_binary_accuracy: 0.9206 - val_mean_absolute_error: 0.1042
Epoch 17/20
5/5 [==============================] - 3s 637ms/step - loss: 0.0606 - binary_accuracy: 0.9177 - mean_absolute_error: 0.1297 - val_loss: 0.0549 - val_binary_accuracy: 0.9209 - val_mean_absolute_error: 0.1034
Epoch 18/20
5/5 [==============================] - 3s 616ms/step - loss: 0.0603 - binary_accuracy: 0.9183 - mean_absolute_error: 0.1282 - val_loss: 0.0550 - val_binary_accuracy: 0.9210 - val_mean_absolute_error: 0.1026
Epoch 19/20
5/5 [==============================] - 3s 619ms/step - loss: 0.0600 - binary_accuracy: 0.9189 - mean_absolute_error: 0.1267 - val_loss: 0.0551 - val_binary_accuracy: 0.9213 - val_mean_absolute_error: 0.1019
Epoch 20/20
5/5 [==============================] - 4s 734ms/step - loss: 0.0596 - binary_accuracy: 0.9193 - mean_absolute_error: 0.1254 - val_loss: 0.0552 - val_binary_accuracy: 0.9213 - val_mean_absolute_error: 0.1013

In [68]:

fig, (ax1, ax2) = plt.subplots(1, 2,
                               figsize=(20, 7))
ax1.plot(loss_history.epoch,
         loss_history.history['mean_absolute_error'], 'r-', label='Training')
ax1.plot(loss_history.epoch,
         loss_history.history['val_mean_absolute_error'], 'b-', label='Validation')
ax1.set_title('Mean Absolute Error')
ax1.legend()

ax2.plot(loss_history.epoch,
         100*np.array(loss_history.history['binary_accuracy']), 'r-', label='Training')
ax2.plot(loss_history.epoch,
         100*np.array(loss_history.history['val_binary_accuracy']), 'b-', label='Validation')
ax2.set_title('Classification Accuracy (%)')
ax2.legend()

Out[68]:

<matplotlib.legend.Legend at 0x11c4efba8>

In [69]:

fig, m_axs = plt.subplots(2, 3,
                          figsize=(18, 8), dpi=150)
for c_ax in m_axs.flatten():
    c_ax.axis('off')
((ax1, ax15, ax2), (ax3, ax4, ax5)) = m_axs
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')
ax15.imshow(t_unet.predict(prep_img(train_img))[0, :, :, 0],
            cmap='viridis', vmin=0, vmax=1)
ax15.set_title('Predicted Training')
ax2.imshow(train_mask, cmap='viridis')
ax2.set_title('Train Mask')

ax3.imshow(cell_img, cmap='bone')
ax3.set_title('Full Image')
unet_pred = t_unet.predict(prep_img(cell_img))[0, :, :, 0]
ax4.imshow(unet_pred,
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Predicted Segmentation')

ax5.imshow(cell_seg,
           cmap='viridis')
ax5.set_title('Ground Truth')

Out[69]:

Text(0.5, 1.0, 'Ground Truth')

Overfitting¶

Having a model with 470,000 free parameters means that it is quite easy to overfit the model by training for too long. Basically what this means is like before the model has gotten very good at the training data but hasn't generalized to other kinds of problems and thus starts to perform worse on regions that aren't exactly the same as the training

In [75]:

t_unet.compile(
    # we use a simple loss metric of mean-squared error to optimize
    loss='mse',
    # we use stochastic gradient descent to optimize
    optimizer=SGD(lr=0.3),
    # we keep track of the number of pixels correctly classified and the mean absolute error as well
    metrics=['binary_accuracy', 'mae']
)

loss_history = t_unet.fit(prep_img(train_img),
                          prep_mask(train_mask),
                          validation_data=(prep_img(valid_img),
                                           prep_mask(valid_mask)),
                          epochs=5)

Train on 1 samples, validate on 1 samples
Epoch 1/5
1/1 [==============================] - 2s 2s/step - loss: 0.0564 - binary_accuracy: 0.9222 - mean_absolute_error: 0.1035 - val_loss: 0.0618 - val_binary_accuracy: 0.9230 - val_mean_absolute_error: 0.0926
Epoch 2/5
1/1 [==============================] - 1s 1s/step - loss: 0.0679 - binary_accuracy: 0.9108 - mean_absolute_error: 0.1123 - val_loss: 0.0733 - val_binary_accuracy: 0.8990 - val_mean_absolute_error: 0.1021
Epoch 3/5
1/1 [==============================] - 1s 1s/step - loss: 0.0749 - binary_accuracy: 0.8888 - mean_absolute_error: 0.1124 - val_loss: 0.0574 - val_binary_accuracy: 0.9260 - val_mean_absolute_error: 0.1007
Epoch 4/5
1/1 [==============================] - 1s 1s/step - loss: 0.0584 - binary_accuracy: 0.9239 - mean_absolute_error: 0.1200 - val_loss: 0.0609 - val_binary_accuracy: 0.9116 - val_mean_absolute_error: 0.0977
Epoch 5/5
1/1 [==============================] - 1s 1s/step - loss: 0.0574 - binary_accuracy: 0.9203 - mean_absolute_error: 0.1073 - val_loss: 0.0573 - val_binary_accuracy: 0.9275 - val_mean_absolute_error: 0.0934

In [76]:

fig, (ax1, ax2) = plt.subplots(1, 2,
                               figsize=(20, 7))
ax1.plot(loss_history.epoch,
         loss_history.history['mean_absolute_error'], 'r-', label='Training')
ax1.plot(loss_history.epoch,
         loss_history.history['val_mean_absolute_error'], 'b-', label='Validation')
ax1.set_title('Mean Absolute Error')
ax1.legend()

ax2.plot(loss_history.epoch,
         100*np.array(loss_history.history['binary_accuracy']), 'r-', label='Training')
ax2.plot(loss_history.epoch,
         100*np.array(loss_history.history['val_binary_accuracy']), 'b-', label='Validation')
ax2.set_title('Classification Accuracy (%)')
ax2.legend()

Out[76]:

<matplotlib.legend.Legend at 0x11f2dec50>

In [79]:

fig, m_axs = plt.subplots(2, 3,
                          figsize=(18, 8), dpi=150)
for c_ax in m_axs.flatten():
    c_ax.axis('off')
((ax1, ax15, ax2), (ax3, ax4, ax5)) = m_axs
ax1.imshow(train_img, cmap='bone')
ax1.set_title('Train Image')
ax15.imshow(t_unet.predict(prep_img(train_img))[0, :, :, 0],
            cmap='viridis', vmin=0, vmax=1)
ax15.set_title('Predicted Training')
ax2.imshow(train_mask, cmap='viridis')
ax2.set_title('Train Mask')

ax3.imshow(cell_img, cmap='bone')
ax3.set_title('Full Image')
unet_pred = t_unet.predict(prep_img(cell_img))[0, :, :, 0]
ax4.imshow(unet_pred,
           cmap='viridis', vmin=0, vmax=1)
ax4.set_title('Predicted Segmentation')

ax5.imshow(cell_seg,
           cmap='viridis')
ax5.set_title('Ground Truth');

In [ ]: