Characterization of Systems in the Time Domain¶

This Jupyter notebook is part of a collection of notebooks in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to Sascha.Spors@uni-rostock.de.

Analysis of a Passive Electrical Network¶

Electrical networks composed of linear passive elements, like resistors, capacitors and inductors can be described by linear ordinary differential equations (ODEs) with constant coefficients. Hence, in view of the theory of signals and systems they can be interpreted as linear time-invariant (LTI) systems. The different ways to characterize the properties of an LTI system introduced before are illustrated at the example of a second-order analog low-pass filter.

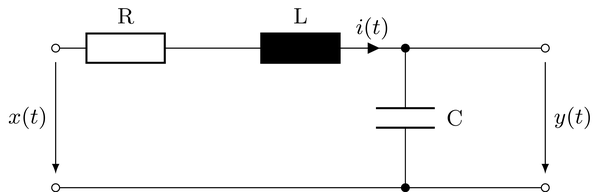
Circuit of a 2nd-order analog low-pass filter

It is assumed that no energy is stored in the capacitor and inductor for $t<0$. It is furthermore assumed that $x(t) = 0$ for $t<0$. Hence $y(t) = 0$ and $\frac{d y(t)}{dt} = 0$ for $t<0$. For illustration, the normalized values $L = 0.5$, $R = 1$, $C = 0.4$ are used for the elements of the electrical network.

Differential Equation¶

The differential equation describing the input/output relation of the electrical network is derived by applying Kirchhoff's circuit laws to the network. This results in the following ODE

\begin{equation} C L \frac{d^2 y(t)}{dt^2} + C R \frac{d y(t)}{dt} + y(t) = x(t) \end{equation}

This ODE is defined in SymPy

In [1]:

import sympy as sym
%matplotlib inline
sym.init_printing()

t, L, R, C = sym.symbols('t L R C', real=True)
x = sym.Function('x')(t)
y = sym.Function('y')(t)

ode = sym.Eq(L*C*y.diff(t, 2) + R*C*y.diff(t) + y, x)
ode

Out[1]:

$$C L \frac{d^{2}}{d t^{2}} y{\left (t \right )} + C R \frac{d}{d t} y{\left (t \right )} + y{\left (t \right )} = x{\left (t \right )}$$

The normalized values of the network elements are stored in a dictionary for later substitution

In [2]:

RLC = {R: 1, L: sym.Rational('.5'), C: sym.Rational('.4')}
RLC

Out[2]:

$$\left \{ C : \frac{2}{5}, \quad L : \frac{1}{2}, \quad R : 1\right \}$$

Impulse Response¶

The passive electrical network and the ODE describing its input/output relation can be interpreted as an LTI system. Hence, the system can be characterized by its impulse response $h(t)$ which is defined as the output of the system for a Dirac Delta impulse $x(t) = \delta(t)$ at the input. For the given system, the impulse response is calculated by explicit solution of the ODE

In [3]:

solution_h = sym.dsolve(
    ode.subs(x, sym.DiracDelta(t)).subs(y, sym.Function('h')(t)))
solution_h

Out[3]:

$$h{\left (t \right )} = C_{1} e^{\frac{t \left(- R - \frac{\sqrt{C \left(C R^{2} - 4 L\right)}}{C}\right)}{2 L}} + C_{2} e^{\frac{t \left(- R + \frac{\sqrt{C \left(C R^{2} - 4 L\right)}}{C}\right)}{2 L}} - \frac{e^{\frac{t \left(- R - \frac{\sqrt{C \left(C R^{2} - 4 L\right)}}{C}\right)}{2 L}} \theta\left(t\right)}{\sqrt{C \left(C R^{2} - 4 L\right)}} + \frac{e^{\frac{t \left(- R + \frac{\sqrt{C \left(C R^{2} - 4 L\right)}}{C}\right)}{2 L}} \theta\left(t\right)}{\sqrt{C \left(C R^{2} - 4 L\right)}}$$

The integration constants $C_1$ and $C_2$ have to be determined from the initial conditions $y(t) = 0$ and $\frac{d y(t)}{dt} = 0$ for $t<0$.

In [4]:

integration_constants = sym.solve((solution_h.rhs.limit(
    t, 0, '-'), solution_h.rhs.diff(t).limit(t, 0, '-')), ['C1', 'C2'])
integration_constants

Out[4]:

$$\left \{ C_{1} : 0, \quad C_{2} : 0\right \}$$

Substitution of the values for the integration constants $C_1$ and $C_2$ into the result from above yields the impulse response of the low-pass

In [5]:

h = solution_h.subs(integration_constants)
h

Out[5]:

$$h{\left (t \right )} = - \frac{e^{\frac{t \left(- R - \frac{\sqrt{C \left(C R^{2} - 4 L\right)}}{C}\right)}{2 L}} \theta\left(t\right)}{\sqrt{C \left(C R^{2} - 4 L\right)}} + \frac{e^{\frac{t \left(- R + \frac{\sqrt{C \left(C R^{2} - 4 L\right)}}{C}\right)}{2 L}} \theta\left(t\right)}{\sqrt{C \left(C R^{2} - 4 L\right)}}$$

The impulse response is plotted for the values of $R$, $L$ and $C$ given above

In [6]:

sym.plot(h.rhs.subs(RLC), (t,-1,10), ylabel=r'h(t)');

Step Response¶

The step response is derived by integrating over the impulse response $h(t)$. For ease of illustration this is performed for the specific values of the elements given above

In [7]:

tau = sym.symbols('tau', real=True)

he = sym.integrate(h.rhs.subs(RLC).subs(t, tau), (tau, 0, t))
he

Out[7]:

$$\frac{5 i \left(- \frac{e^{t \left(-1 - 2 i\right)}}{5} + \frac{2 i e^{t \left(-1 - 2 i\right)}}{5} + \frac{1}{5} - \frac{2 i}{5}\right) \theta\left(t\right)}{4} - \frac{5 i \left(- \frac{e^{t \left(-1 + 2 i\right)}}{5} - \frac{2 i e^{t \left(-1 + 2 i\right)}}{5} + \frac{1}{5} + \frac{2 i}{5}\right) \theta\left(t\right)}{4}$$

Let's plot the step response

In [8]:

sym.plot(he, (t,-1,10), ylabel=r'$h_\epsilon(t)$');

Transfer Function¶

For an exponential input signal $x(t) = e^{s t}$, the transfer function $H(s)$ represents the complex weight of the exponential output signal $y(t) = H(s) \cdot e^{s t}$. The transfer function is derived by introducing $x(t)$ and $y(t)$ into the ODE and solving for $H(s)$

In [9]:

s = sym.symbols('s')
H = sym.Function('H')(s)

H, = sym.solve(ode.subs(x, sym.exp(s*t)).subs(y, H*sym.exp(s*t)).doit(), H)
H

Out[9]:

$$\frac{1}{C L s^{2} + C R s + 1}$$

The transfer characteristic of an LTI system for harmonic exponential signals $e^{j \omega t} = \cos(\omega t) + j \sin(\omega t)$ is of special interest for the analysis of electrical circuits. It can be derived from $H(s)$ by substituting the complex frequency $s$ by $s = j \omega$. The resulting transfer function $H(j \omega)$ provides the attenuation/amplification and phase the system adds to an harmonic input signal.

In [10]:

w = sym.symbols('omega', real=True)

Hjw = H.subs(s, sym.I * w)
Hjw

Out[10]:

$$\frac{1}{- C L \omega^{2} + i C R \omega + 1}$$

The magnitude of the transfer function $|H(j \omega)|$ is plotted for illustration for the specific values of the elements given above

In [11]:

sym.plot(abs(Hjw.subs(RLC)), (w, -10, 10),
         ylabel=r'$|H(j \omega)|$', xlabel=r'$\omega$');

It now becomes obvious, that the low frequencies pass through the system and that high frequencies are attenuated. This motivates the term 'low-pass' for such systems.

As alternative to the solution of the ODE, the transfer function $H(s)$ is computed from the impulse response and plotted for the specific values of the elements given above

In [12]:

H2 = sym.integrate(h.rhs.subs(RLC)*sym.exp(-s*t), (t, 0, sym.oo), conds='none')
H2.simplify()

Out[12]:

$$\frac{5}{s^{2} + 2 s + 5}$$

In [13]:

sym.plot(abs(H2.subs(s, sym.I*w)), (w, -10, 10),
         ylabel=r'$|H(j \omega)|$', xlabel=r'$\omega$');

The phase of the transfer function $\varphi(j \omega) = \arg \{ H(j \omega) \}$ provides insight into the phase added to an harmonic signal when passing through the system. It is computed and plotted for the specific values of the elements given above

In [14]:

phi = sym.arg(Hjw)
sym.plot(phi.subs(RLC), (w, -10, 10),
         ylabel=r'$\varphi(j \omega)$', xlabel=r'$\omega$');

Copyright

The notebooks are provided as Open Educational Resource. Feel free to use the notebooks for your own educational purposes. The text is licensed under Creative Commons Attribution 4.0, the code of the IPython examples under the MIT license. Please attribute the work as follows: Lecture Notes on Signals and Systems by Sascha Spors.