Notebook

Characterization of Systems in the Time Domain¶

This Jupyter notebook is part of a collection of notebooks in the bachelors module Signals and Systems, Communications Engineering, Universität Rostock. Please direct questions and suggestions to Sascha.Spors@uni-rostock.de.

Analysis of a Damped Spring Pendulum¶

The damped spring pendulum is an example for a mechanical system that can be modeled by a linear ordinary differential equation (ODE) with constant coefficients. In view of the theory of signals and systems it hence can be interpreted as a linear time-invariant (LTI) system. The mechanical properties of the damped spring pendulum are analyzed by using the theory of LTI systems. The underlying mechanical setup is depicted in the following

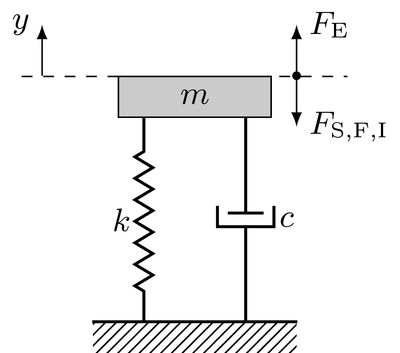
Damped spring pendulum

A compact mass $m$ is mounted on a spring with stiffness $k$ which is connected to the ground. A damper with viscous damping coefficient $c$ is mounted parallel to the spring to model the friction present in the system. It is assumed that the movement of the mass over time is restricted to the vertical axis, here denoted by $y$. It is further assumed that the mass is in its idle position for $t<0$. The pretension of the spring by the mass can be neglected this way. It is additionally assumed that the mass is not moving for $t<0$. Denoting the displacement of the mass over time with $y(t)$, these initial conditions are formulated as $y(t) = 0$ and $\frac{d y(t)}{dt} = 0$ for $t<0$.

The normalized values $m = 0.1$, $c = 0.1$, $k = 2.5$ are used for illustration in the following.

Differential Equation¶

The differential equation of the mechanical system is derived by considering the force equilibrium at the mass

\begin{equation} F_\text{S}(t) + F_\text{F}(t) + F_\text{I}(t) = F_\text{E}(t) \end{equation}

where $F_\text{E}(t)$ denotes an external force acting onto the mass, the other forces are derived in the sequel. The force $F_\text{S}(t)$ induced by the spring is given by Hooke's law

\begin{equation} F_\text{S}(t) = k y(t) \end{equation}

Its common to model the frictional force $F_\text{F}(t)$ induced by the damper as being proportional to the velocity of the mass

\begin{equation} F_\text{F}(t) = c \frac{d y(t)}{dt} \end{equation}

The inertial force $F_\text{I}(t)$ due to the acceleration of the mass is given as

\begin{equation} F_\text{I}(t) = m \frac{d^2 y(t)}{dt^2} \end{equation}

Introducing the forces into the force equilibrium yields the differential equation describing the displacement of the damped spring pendulum

\begin{equation} m \frac{d^2 y(t)}{dt^2} + c \frac{d y(t)}{dt} + k y(t) = F_\text{E}(t) \end{equation}

as a consequence of the external force. Above equation constitutes an ODE with constant coefficients. It can be interpreted as an LTI system with the external force as input signal $x(t) = F_\text{E}(t)$ and the displacement of the mass as output signal $y(t)$.

Comparison to Passive Electrical Networks¶

Comparing the ODEs of the damped spring pendulum and the second-order analog low-pass yields that both constitute second-order ODEs with constant coefficients. Dividing the ODE of the second-order analog low pass by $C$ results in

\begin{equation} L \frac{d^2 u_\text{o}(t)}{dt^2} + R \frac{d u_\text{o}(t)}{dt} + \frac{1}{C} u_\text{o}(t) = \frac{1}{C} u_\text{i}(t) \end{equation}

where $u_\text{i}(t)$ and $u_\text{o}(t)$ denote the in- and output voltage of the analog circuit. Comparison with above ODE of the spring pendulum yields the equivalence of both systems for

	2nd-order low-pass	spring pendulum
input signal $x(t)$	$u_\text{i}(t) = F_\text{E}(t) C$	$F_\text{E}(t) = \frac{u_\text{i}(t)}{C}$
output signal $y(t)$	$u_\text{o}(t)$	$y(t)$
	$L = m$	$m = L$
	$R = c$	$c = R$
	$C = \frac{1}{k}$	$k = \frac{1}{C}$

Note, the equivalence between mechanical systems described by ODEs with constant coefficients and analog circuits was used to simulate such systems by analog computers.

Impulse Response¶

The LTI system corresponding to the pendulum can be characterized by its impulse response $h(t)$. It is defined as the output of the system for a Dirac Delta impulse $x(t) = \delta(t)$ at the input. Physically this can be approximated by hitting the mass (very shortly and forceful). The impulse response characterizes the movement $y(t)$ of the mass after such an event.

First the ODE of the spring pendulum is defined in SymPy

In [1]:

import sympy as sym
%matplotlib inline
sym.init_printing()

t, m, c, k = sym.symbols('t m c k', real=True)
x = sym.Function('x')(t)
y = sym.Function('y')(t)

ode = sym.Eq(m*y.diff(t, 2) + c*y.diff(t) + k*y, x)
ode

Out[1]:

$$c \frac{d}{d t} y{\left (t \right )} + k y{\left (t \right )} + m \frac{d^{2}}{d t^{2}} y{\left (t \right )} = x{\left (t \right )}$$

The normalized values of the physical constants are stored in a dictionary for ease of later substitution

In [2]:

mck = {m: 0.1, c: sym.Rational('.1'), k: sym.Rational('2.5')}
mck

Out[2]:

$$\left \{ c : \frac{1}{10}, \quad k : \frac{5}{2}, \quad m : 0.1\right \}$$

The impulse response is calculated by explicit solution of the ODE.

In [3]:

solution_h = sym.dsolve(
    ode.subs(x, sym.DiracDelta(t)).subs(y, sym.Function('h')(t)))
solution_h

Out[3]:

$$h{\left (t \right )} = C_{1} e^{\frac{t \left(- c - \sqrt{c^{2} - 4 k m}\right)}{2 m}} + C_{2} e^{\frac{t \left(- c + \sqrt{c^{2} - 4 k m}\right)}{2 m}} - \frac{e^{\frac{t \left(- c - \sqrt{c^{2} - 4 k m}\right)}{2 m}} \theta\left(t\right)}{\sqrt{c^{2} - 4 k m}} + \frac{e^{\frac{t \left(- c + \sqrt{c^{2} - 4 k m}\right)}{2 m}} \theta\left(t\right)}{\sqrt{c^{2} - 4 k m}}$$

The integration constants $C_1$ and $C_2$ have to be determined from the initial conditions $y(t) = 0$ and $\frac{d y(t)}{dt} = 0$ for $t<0$.

In [4]:

integration_constants = sym.solve((solution_h.rhs.limit(
    t, 0, '-'), solution_h.rhs.diff(t).limit(t, 0, '-')), ['C1', 'C2'])
integration_constants

Out[4]:

$$\left \{ C_{1} : 0, \quad C_{2} : 0\right \}$$

Substitution of the values for the integration constants $C_1$ and $C_2$ into the result from above yields the impulse response of the spring pendulum

In [5]:

h = solution_h.subs(integration_constants)
h

Out[5]:

$$h{\left (t \right )} = - \frac{e^{\frac{t \left(- c - \sqrt{c^{2} - 4 k m}\right)}{2 m}} \theta\left(t\right)}{\sqrt{c^{2} - 4 k m}} + \frac{e^{\frac{t \left(- c + \sqrt{c^{2} - 4 k m}\right)}{2 m}} \theta\left(t\right)}{\sqrt{c^{2} - 4 k m}}$$

The impulse response is plotted for the specific values of $m$, $c$ and $k$ given above

In [6]:

sym.plot(h.rhs.subs(mck), (t, 0, 12), ylabel=r'h(t)');

Transfer Function¶

For an exponential input signal $x(t) = e^{s t}$, the transfer function $H(s)$ represents the weight of the exponential output signal $y(t) = H(s) \cdot e^{s t}$. The transfer function is derived by introducing $x(t)$ and $y(t)$ into the ODE and solving for $H(s)$

In [7]:

s = sym.symbols('s')
H = sym.Function('H')(s)

H, = sym.solve(ode.subs(x, sym.exp(s*t)).subs(y, H*sym.exp(s*t)).doit(), H)
H

Out[7]:

$$\frac{1}{c s + k + m s^{2}}$$

The transfer characteristic of an LTI system for harmonic exponential signals $e^{j \omega t} = \cos(\omega t) + j \sin(\omega t)$ is of special interest in the analysis of resonating systems. It can be derived from $H(s)$ by substituting the complex frequency $s$ with $s = j \omega$. The resulting transfer function $H(j \omega)$ provides the attenuation and phase the system adds to an harmonic input signal.

In [8]:

w = sym.symbols('omega', real=True)

Hjw = H.subs(s, sym.I * w)
Hjw

Out[8]:

$$\frac{1}{i c \omega + k - m \omega^{2}}$$

The magnitude of the transfer function $|H(j \omega)|$ is plotted for the specific values of the elements given above

In [9]:

sym.plot(abs(Hjw.subs(mck)), (w, -15, 15),
         ylabel=r'$|H(j \omega)|$', xlabel=r'$\omega$');

When inspecting the magnitude of the transfer function it becomes evident that the damped spring pendulum shows resonances (maxima) for two specific angular frequencies. These resonance frequencies $\omega_0$ are calculated by inspecting the extreme values of $|H(j \omega)|$. First the derivative of $|H(j \omega)|$ with respect to $\omega$ is computed and set to zero

In [10]:

extrema = sym.solve(sym.Eq(sym.diff(abs(Hjw), w),0),w)
extrema

Out[10]:

$$\left [ 0, \quad - \frac{\sqrt{- \frac{c^{2}}{2} + k m}}{m}, \quad \frac{\sqrt{- \frac{c^{2}}{2} + k m}}{m}\right ]$$

For the maxima of the transfer function only the 2nd and 3rd extrema are of interest

In [11]:

w0 = extrema[1:3]
w0

Out[11]:

$$\left [ - \frac{\sqrt{- \frac{c^{2}}{2} + k m}}{m}, \quad \frac{\sqrt{- \frac{c^{2}}{2} + k m}}{m}\right ]$$

The resonance frequencies are computed for the specific values of $m$, $c$ and $k$ given above

In [12]:

[w00.subs(mck) for w00 in w0]

Out[12]:

$$\left [ -4.94974746830583, \quad 4.94974746830583\right ]$$

The phase of the transfer function $\varphi(j \omega)$ is computed and plotted for the specific values of the elements given above

In [13]:

phi = sym.arg(Hjw)
sym.plot(phi.subs(mck), (w, -15, 15),
         ylabel=r'$\varphi(j \omega)$', xlabel=r'$\omega$');

Exercise

Change the viscous damping coefficient $c$ of the spring pendulum and investigate how the magnitude and phase of the transfer function $H(j \omega)$ changes.
How does the frequency of the damped harmonic oscillation in the impulse response relates to the resonance frequency?

Application: Vibration Isolation¶

An application of above example is the design of vibration isolation by a damped spring pendulum. A typical example is a rotating machinery with mass $m$ which has some sort of imbalance. Assuming that the imbalance can be modeled as a rotating mass, the external force $F_\text{E}(t)$ is given by the vertical component of its centrifugal force

\begin{equation} F_\text{E}(t) = F_0 \sin(\omega t) = F_0 \cdot \Im \{e^{j \omega t} \} \end{equation}

where $\omega$ denotes the angular frequency of the rotating machinery and

\begin{equation} F_0 = m_\text{I} r \omega^2 \end{equation}

the amplitude of the force with $m_\text{I}$ denoting the mass of the imbalance and $r$ the radius of its circular orbit. Since $e^{j \omega t}$ is an eigenfunction of the LTI system, the resulting displacement is then given as

\begin{equation} y(t) = F_0 \cdot \Im \{e^{j \omega t} H(j \omega) \} \end{equation}

The aim of vibration isolation is to keep the magnitude of the displacement as low as possible.

Exercise

Compute and plot the displacement for given $m_\text{I}$ and $r$.
For which angular frequencies $\omega$ is the magnitude of the displacement largest? How is the phase relation between the external force $F_\text{E}(t)$ and displacement $y(t)$ at these frequencies?
How should the resonance frequencies $\omega_0$ of the spring pendulum be chosen in order to get a good vibration isolation for a machine rotating with angular frequency $\omega$? How is the phase relation between the external force $F_\text{E}(t)$ and displacement $y(t)$ at this frequency?

Copyright

The notebooks are provided as Open Educational Resource. Feel free to use the notebooks for your own educational purposes. The text is licensed under Creative Commons Attribution 4.0, the code of the IPython examples under the MIT license. Please attribute the work as follows: Lecture Notes on Signals and Systems by Sascha Spors.