Pseudopotentials¶
In this example, we'll look at how to use various pseudopotential (PSP) formats in DFTK and discuss briefly the utility and importance of pseudopotentials.
Currently, DFTK supports norm-conserving (NC) PSPs in separable (Kleinman-Bylander) form. Two file formats can currently be read and used: analytical Hartwigsen-Goedecker-Hutter (HGH) PSPs and numeric Unified Pseudopotential Format (UPF) PSPs.
In brief, the pseudopotential approach replaces the all-electron atomic potential with an effective atomic potential. In this pseudopotential, tightly-bound core electrons are completely eliminated ("frozen") and chemically-active valence electron wavefunctions are replaced with smooth pseudo-wavefunctions whose Fourier representations decay quickly. Both these transformations aim at reducing the number of Fourier modes required to accurately represent the wavefunction of the system, greatly increasing computational efficiency.
Different PSP generation codes produce various file formats which contain the same general quantities required for pesudopotential evaluation. HGH PSPs are constructed from a fixed functional form based on Gaussians, and the files simply tablulate various coefficients fitted for a given element. UPF PSPs take a more flexible approach where the functional form used to generate the PSP is arbitrary, and the resulting functions are tabulated on a radial grid in the file. The UPF file format is documented on the Quantum Espresso Website.
In this example, we will compare the convergence of an analytical HGH PSP with a modern numeric norm-conserving PSP in UPF format from PseudoDojo. Then, we will compare the bandstructure at the converged parameters calculated using the two PSPs.
using DFTK
using Unitful
using Plots
using LazyArtifacts
import Main: @artifact_str # hide
Here, we will use a Perdew-Wang LDA PSP from PseudoDojo,
which is available in the JuliaMolSim
PseudoLibrary.
Directories in PseudoLibrary correspond to artifacts that you can load using artifact
strings which evaluate to a filepath on your local machine where the artifact has been
downloaded.
We load the HGH and UPF PSPs using load_psp, which determines the
file format using the file extension. The artifact string literal resolves to the
directory where the file is stored by the Artifacts system. So, if you have your own
pseudopotential files, you can just provide the path to them as well.
psp_hgh = load_psp("hgh/lda/si-q4.hgh");
psp_upf = load_psp(artifact"pd_nc_sr_lda_standard_0.4.1_upf/Si.upf");
┌ Warning: using Pkg instead of using LazyArtifacts is deprecated │ caller = eval at boot.jl:370 [inlined] └ @ Core ./boot.jl:370 Downloading artifact: pd_nc_sr_lda_standard_0.4.1_upf
First, we'll take a look at the energy cutoff convergence of these two pseudopotentials. For both pseudos, a reference energy is calculated with a cutoff of 140 Hartree, and SCF calculations are run at increasing cutoffs until 1 meV / atom convergence is reached.
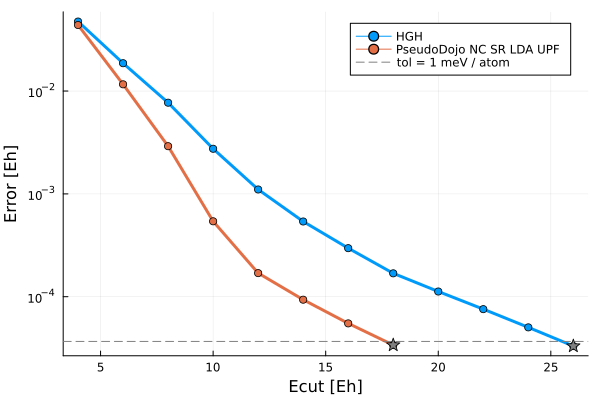
The converged cutoffs are 26 Ha and 18 Ha for the HGH and UPF pseudos respectively. We see that the HGH pseudopotential is much harder, i.e. it requires a higher energy cutoff, than the UPF PSP. In general, numeric pseudopotentials tend to be softer than analytical pseudos because of the flexibility of sampling arbitrary functions on a grid.
Next, to see that the different pseudopotentials give reasonbly similar results, we'll look at the bandstructures calculated using the HGH and UPF PSPs. Even though the convered cutoffs are higher, we perform these calculations with a cutoff of 12 Ha for both PSPs.
function run_bands(psp)
a = 10.26 # Silicon lattice constant in Bohr
lattice = a / 2 * [[0 1 1.];
[1 0 1.];
[1 1 0.]]
Si = ElementPsp(:Si; psp=psp)
atoms = [Si, Si]
positions = [ones(3)/8, -ones(3)/8]
# These are (as you saw above) completely unconverged parameters
model = model_LDA(lattice, atoms, positions; temperature=1e-2)
basis = PlaneWaveBasis(model; Ecut=12, kgrid=(4, 4, 4))
scfres = self_consistent_field(basis; tol=1e-4)
bandplot = plot_bandstructure(scfres)
(; scfres, bandplot)
end;
The SCF and bandstructure calculations can then be performed using the two PSPs, where we notice in particular the difference in total energies.
result_hgh = run_bands(psp_hgh)
result_hgh.scfres.energies
n Energy log10(ΔE) log10(Δρ) Diag Δtime
--- --------------- --------- --------- ---- ------
1 -7.920957479671 -0.69 5.8
2 -7.925542392116 -2.34 -1.22 1.8 255ms
3 -7.926171322515 -3.20 -2.43 2.6 310ms
4 -7.926189619175 -4.74 -3.03 3.9 353ms
5 -7.926189835143 -6.67 -4.18 2.4 293ms
Computing bands along kpath:
Γ -> X -> U and K -> Γ -> L -> W -> X
Diagonalising Hamiltonian kblocks: 100%|████████████████| Time: 0:00:09
Energy breakdown (in Ha):
Kinetic 3.1590147
AtomicLocal -2.1424946
AtomicNonlocal 1.6043334
Ewald -8.4004648
PspCorrection -0.2948928
Hartree 0.5515699
Xc -2.4000934
Entropy -0.0031621
total -7.926189835143
result_upf = run_bands(psp_upf)
result_upf.scfres.energies
n Energy log10(ΔE) log10(Δρ) Diag Δtime
--- --------------- --------- --------- ---- ------
1 -8.515349267300 -0.93 6.0
2 -8.518471659081 -2.51 -1.44 1.5 250ms
3 -8.518846413170 -3.43 -2.78 3.2 329ms
4 -8.518860720679 -4.84 -3.19 4.6 422ms
5 -8.518860783871 -7.20 -3.52 2.2 271ms
6 -8.518860826649 -7.37 -4.82 1.4 257ms
Computing bands along kpath:
Γ -> X -> U and K -> Γ -> L -> W -> X
Diagonalising Hamiltonian kblocks: 100%|████████████████| Time: 0:00:09
Energy breakdown (in Ha):
Kinetic 3.0954179
AtomicLocal -2.3650757
AtomicNonlocal 1.3082644
Ewald -8.4004648
PspCorrection 0.3951970
Hartree 0.5521859
Xc -3.1011662
Entropy -0.0032193
total -8.518860826649
But while total energies are not physical and thus allowed to differ, the bands (as an example for a physical quantity) are very similar for both pseudos:
plot(result_hgh.bandplot, result_upf.bandplot, titles=["HGH" "UPF"], size=(800, 400))