Notebook

Основы статистики¶

конспект лекций¶

Автор лекций: святой Анатолий Карпов

Конспектировал: отрок Михаил Курочкин

telegram: @mikhail_kurochkin
instagram: mikhail_k17 если хотите вообще от души поблагодарить - подписка/лайк :)

Содержание¶

Часть 1¶

Генеральная совокупность и выборка¶

Генеральная совокупность (от лат. generis — общий, родовой) — совокупность всех объектов, относительно которых предполагается делать выводы при изучении конкретной задачи. Далее ГС.
Репрезентативная выборка – это такая выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности.

Способы репрезентативной выборки:¶

Простая случайная выборка (simple random sample)
Стратифицированная выборка (stratified sample) – разделение ГС на страты (группы) а оттуда уже делается случайная выборка.
Групповая выборка (cluster sample) – похожие группы выбираются из выборки и далее делается случайная выборка (например, районы одного города)

групповая выборка	Стратифицированная выборка
Выборка формируется только из несколько субпопуляций (кластеров)	Выборка формируется из всех субпопуляций (страт)
В пределах кластера элементы должны быть разнородны, тогда как поддерживается однородность или схожесть между разными кластерами	В пределах страты элементы должны быть однородны, а между стратами должна быть разнородность (различия)
Схема выборки нужна только для кластеров, попавших в выборку	Должна быть сформирована полная схема выборки для всех стратифицированных субпопуляций
Повышает эффективность выборки, уменьшая стоимость	Повышает точность

Типы переменных¶

Количественные – измеряемое (например, рост):
Непрерывные – переменная принимает любое значение на опр. промежутке;
Дискретные – только определенные значения (3.5 ребенка в семье не будет).
Номинативные (= качественные) – разделение испытуемых на группы, цифры как маркеры (например: 1 -женщины, 2 – мужчины). Цифры как имена групп, не для расчетов.
Ранговые – похоже на номинативные, только возможны сравнения (быстрее/медленнее и т.п.)

Описательная статистика¶

Глоссарий:¶

Эмпирические данные - данные полученные опытным путём.
Описательная (дескриптивная) статистика - обработка данных полученных эмпирическим путём и их систематизация, наглядное представление в форме графиков, таблиц, а также их количественное описание посредством основных статистических показателей.
Распределение вероятностей - это закон, описывающий область значений случайной величины и вероятность её появления (частоту) в данной области. То есть насколько часто X появляется в данном диапазоне значений.
Гистограмма частот - ступенчатая функция показывающая насколько часто вероятно появление величины в указанном диапазоне значений.

Меры центральной тенденции¶

тип описательной статистики

Мода¶

Это значение признака, которое встречается максимально часто. В выборке может быть несколько или одна мода.

Медиана¶

Это значение признака, которое делит упорядочное множество попалам. Если множество содержит чётное количество элементов, то берётся среднее из двух серединных элементов упорядочного множества.

Среднее значение¶

Cумма всех значений измеренного признака делится на количество измеренных значений.

Свойства среднего значения¶

$$M_{x + c} = \frac{\sum_{i=1}^{n}{(x_{i} + c)}}{n} = \frac{\sum_{i=1}^{n} x_{i}}{n} + \frac{\sum_{i=1}^{n} c}{n} = M_{x} + \frac{nc}{n} = M_{x} + c$$$$M_{x * c} = \frac{\sum_{i=1}^{n}{(x_{i} * c)}}{n} = \frac{c * \sum_{i=1}^{n} x_{i}}{n} = c * M_{x}$$$$\sum_{i=1}^{n} (x_{i} - M_{x}) = nM_{x} - nM_{x} = 0$$

1.Примеры¶

In [1]:

'''Расчёт моды, медианы и среднего с помощью библиотек numpy и scipy'''
import numpy as np
from scipy import stats
sample = np.array([185, 175, 170, 169, 171, 175, 157, 172, 170, 172, 167, 173, 168, 167, 166,
              167, 169, 172, 177, 178, 165, 161, 179, 159, 164, 178, 172, 170, 173, 171])
# в numpy почему-то нет моды
print('mode:', stats.mode(sample))
print('median:', np.median(sample))
print('mean:', np.mean(sample))

mode: ModeResult(mode=array([172]), count=array([4]))
median: 170.5
mean: 170.4

In [2]:

'''Расчёт моды, медианы и среднего с помощью библиотеки pandas'''
import pandas as pd
sample = pd.Series([185, 175, 170, 169, 171, 175, 157, 172, 170, 172, 167, 173, 168, 167, 166,
              167, 169, 172, 177, 178, 165, 161, 179, 159, 164, 178, 172, 170, 173, 171])

print('mode:', sample.mode())
print('median:', sample.median())
print('mean:', sample.mean())

mode: 0    172
dtype: int64
median: 170.5
mean: 170.4

Меры изменчивости¶

Размах¶

Это разность между максимальным и минимальным значениям выборки. Крайне чувствителен к взбросам.

Дисперсия¶

Это средний квадрат отклонений индивидуальных значений признака от их средней величины

Для генеральной совокупности¶

$$D = \frac{\sum_{i=1}^{n} (x_{i} - M_{x})^2}{n}$$

Среднеквадратическое отклонение $$ \sigma = \sqrt{D}$$

Для выборки¶

$$D = \frac{\sum_{i=1}^{n} (x_{i} - M_{x})^2}{n-1}$$

где 1 это количество степеней свободы Важно отменить, что среднеквадратическое отклонение для выборки обозначают по другому, как sd - standart deviation

Ликбез: Почему именно квадрат, а не модуль или куб?¶

Могу предположить, что линейное отклонение более чувствительно выбросам, квадратичное менее, кубическое — ещё менее чувствительно. Попробовал посчитать для 3-х выборок: [1,2,3,4,5], [1,2,3,4,50] и [1,2,3,4,500]:

Линейное: 2.5, 452.5 и 49502.5
Квадратичное: 1.58, 21.27 и 222.49
Кубическое: 1.36, 7.68, и 36.71

Модуль не берут потому, что модуль - не гладкая функция. В нуле у модуля имеется "излом" из-за которого у производной происходит разрыв. А очень многие математические теоремы, которые наверняка потребуются дальше, работают только на гладких функциях.

Вообще, с не гладкими функциями работать не любят. Там все становится сложнее. Поэтому берется квадрат. Source

Свойства дисперсии¶

$$ D_{x+c} = D_x $$$$ D_{x*c} = D_x+c^2 $$

Квартили распределения¶

Квартили - это три точки(значения признака), которые делят упорядочное множество данных на 4 равные части.

Box plot - такой вид диаграммы в удобной форме показывает медиану, нижний и верхний квартили, минимальное и максимальное значение выборки и выбросы.

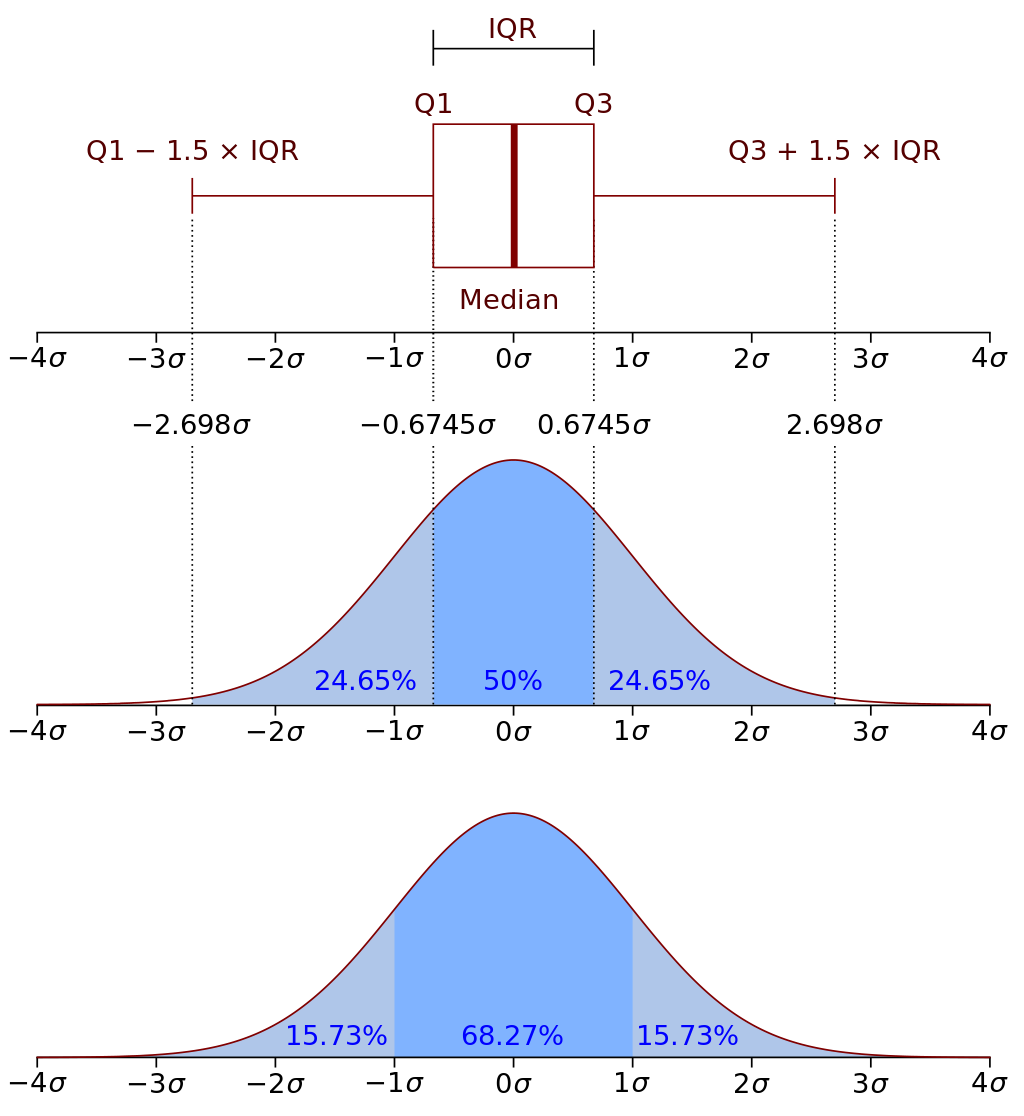
Квартили и inter quartile range используют, чтобы оценить наличие выбросов. Алгоритм расчета - посчитали квартили, посчитали разницу между ними, вычислили теоретический максимум и минимум, сравнили с имеющимся и выяснили есть ли у вас выбросы и сколько их. Если много, то нужно анализировать и решать брать ли их в выборку или нет.

2.Пример¶

In [3]:

'''Расчитываем размах и стандартное отклонение с помощью numpy'''
import numpy as np
sample = np.array([185, 175, 170, 169, 171, 175, 157, 172, 170, 172, 167, 173, 168, 167, 166,
              167, 169, 172, 177, 178, 165, 161, 179, 159, 164, 178, 172, 170, 173, 171])

# The name of the function comes from the acronym for ‘peak to peak’.
print(f'Range: {np.ptp(sample)} is equal max - min: {np.max(sample)- np.min(sample)}')

# ddof - Delta Degrees of Freedom
print(f'Standard deviation: {np.std(sample, ddof=1):.2f}')

Range: 28 is equal max - min: 28
Standard deviation: 6.00

Диаграмма boxplot¶

In [4]:

'''с помощью диаграммы boxplot мы можем узнать медиану, 2 и 3 квартиль'''
import matplotlib.pyplot as plt


plt.boxplot(sample, showfliers=1)
plt.show()

Нормальное распределение¶

Коротко

Унимодально
Симметрично
Отклонения наблюдений от среднего подчиняются определённому вероятностному закону

Подробно

Нормальное распределение возникает в результате воздействия множества факторов, вклад каждого из которых очень мал.

Для облегчения этого восприятия в 1873 году Фрэнсис Гальтон сделал устройство, которое в последствии назвали Доской Галтона (или квинкункс). Суть простая: сверху по середине подаются шарики, которые при прохождении нескольких уровней (например, 10-ти) на каждом уровне сталкиваются с препятствием, и при каждом столкновении отскакивают либо влево, либо вправо (с равной вероятностью).

Как вы догадываетесь, результатом прохождения - это распределение, стремящееся к нормальному!

Выглядит это так:

Или в виде кода:

In [5]:

'''Иммитация доски Гальтона в коде'''
import seaborn as sns
data = dict()
# количество шариков
N = 10000
# количество уровней
level = 20
for _ in range(N):
    index = 0
    for _ in range(level):
        index += np.random.choice([-1, 1])
    data.setdefault(index, 0)
    data[index] += 1
sns.barplot(x=list(data.keys()), y=list(data.values()));

Z-преобразование¶

Преобразование полученных данных в стандартную Z-шкалу (Z-scores) со средним значением = 0 и дисперсией = 1. Чтобы привести к такому виду из каждого наблюдения нужно отнять среднее значение и разделитьв на стандартное отклонение.

$$ Z_{i}=\frac{x_{i} - \bar{X}}{sd} $$

Иногда нам необходимо рассчитать z - значение только для отдельно взятого наблюдения, чтоб выяснить насколько далеко оно отклоняется от среднего значения в единицах стандартного отклонения.

Правило 3х-сигм¶

3.Примеры¶

In [6]:

''' Считается, что значение IQ (уровень интеллекта) у людей имеет нормальное распределение
со средним значением равным 100 и стандартным отклонением равным 15 (M = 100, sd = 15).
Какой приблизительно процент людей обладает IQ > 125?
'''

from scipy import stats
mean = 100
std = 15
IQ=125
# sf - Survival function = (1 - cdf) - Cumulative distribution function
print(f"Только у {(stats.norm(mean, std).sf(IQ))*100:.2f}% людей, IQ>{IQ}")

Только у 4.78% людей, IQ>125

Центральная предельная теорема¶

Гласит, что множество средних выборок из генеральной совокупности (ГС необязательно иметь нормальное распределние) будут иметь нормальное распределение. Причём средняя этого распределения будет близко к средней генеральной совокупности, а стандарное отклонение этого распределение будет називаться стандарной ошибкой среднего (se).

Зная стандартное отклонение ГС и размер выборки мы можем рассчитать стандартную ошибку среднего.

$$ se = \frac{\sigma}{\sqrt{N}} $$

где N - размер выборки. Если размер выборки достаточно большой (>30) и она является репрезативна, то вместо стандарного отклонения ГС мы можем взять стандарное отклонение выборки.

$$ se = \frac{sd}{\sqrt{N}} $$

Стандартная ошибка среднего - это среднеквадратическое отклонение распределения выборочных средних

4.Примеры¶

Проверим на практике все эти законы.

In [7]:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math

# значения игральной кости
dice = [1, 2, 3, 4, 5, 6]
# количество бросков кости
count = 6
# размер генеральной совокупность
sp_size = 10000
# sp - Statistical population - генеральная совокупность
sp = pd.Series(dtype=np.int64, index=range(sp_size))
for i in range(sp_size):
    value = 0
    for _ in range(count):
        value += np.random.choice(dice)
    sp[i] = value

sp.plot.hist(bins=28)

Out[7]:

<AxesSubplot:ylabel='Frequency'>

In [8]:

# количество выборок
samples_count = 10
# размер выборки
sample_size = 200
samples = pd.DataFrame([
    [np.random.choice(sp) for _ in range(sample_size)] for __ in range(samples_count)
]).T

samples.hist(figsize=(16, 10), sharex=0)
plt.subplots_adjust(hspace = 0.6)

In [9]:

means = samples.mean()
print('сравним среднию ГС и среднию средних выборок', sp.mean(), means.mean())
print('разница:', abs(means.mean() - sp.mean()), ', стандартная ошибка среднего:', means.std())

сравним среднию ГС и среднию средних выборок 20.9891 20.966
разница: 0.023099999999999454 , стандартная ошибка среднего: 0.16899704139422084

In [10]:

# возмем произвольную выборку 
sample = samples[0]
print('sample mean:', sample.mean())
print('sample SE: ', sample.std()/math.sqrt(sample.size))

sample mean: 21.065
sample SE:  0.28699425694182085

PS Важное замечание о ЦПТ номер 2.¶

Пожалую самый сложный момент - это как мы так взяли и заменили стандартное отклонение генеральной совокупности на выборочное. Ну и что с того, что у нас выборка объемом больше 30 наблюдений, что за магическое число такое?

Все правильно, никакой магии не происходит. И совсем скоро мы в этом окончательно разберемся. Как только пройдем тему t - распределения во втором модуле. Вот тут я подробно расписал, как же нам нужно рассчитывать стандартную ошибку среднего, если мы не знаем стандартное отклонение в генеральной совокупности.

Доверительные интервалы для среднего¶

Если мы имеем некоторую выборку и ГС, то мы не можем точно знать среднюю ГС, зная только среднее выборки. Однако мы можем сказать, с некоторым процентом уверенности, в каком интервале лежит средняя ГС. Понятно дело, что для нас лучше, чтобы этот интервал был как можно меньше, как это сделать?

Мы знаем, средняя средних выборок, стремится к средней ГС, также мы знаем, что стандартная ошибка среднего описывает стандартное отклонение распределения средних выборок. Если мы возьмём случайную выборку $X$ и найдём её среднее $\bar{X}$, а также вычислим стандартную ошибку $se$, то мы можем вычислить доверительный интевал $[\bar{X} - 1.96*se; \bar{X} + 1.96*se]$ который описывает среднюю ГС с некотором интервале с 95% доверия.

Загадочное число 1,96 это количество сигм $\sigma$ в нормальном распределение, необходимые, чтобы охватить 95% значений в этом распределнии.

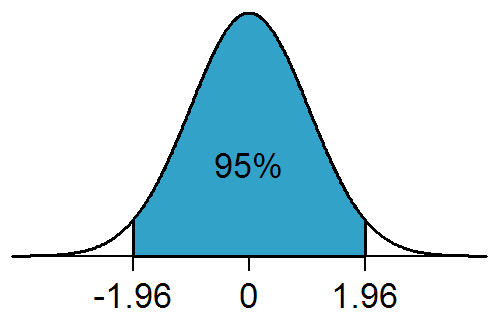
Если мы рассчитали 95% доверительный интервал для среднего значения, это значит:¶

Среднее значение в генеральной совокупности точно принадлежит рассчитанному доверительному интервалу.
Мы можем быть на 95% уверены, что среднее значение в генеральной совокупности принадлежит рассчитанному доверительному интервалу.
Если многократно повторять эксперимент, для каждой выборки рассчитывать свой доверительный интервал, то в 95 % случаев истинное среднее будет находиться внутри доверительного интервала.
Среднее значение в генеральной совокупности точно превышает нижнюю границу 95% доверительного интервала.
Если многократно повторять эксперимент, то 95 % выборочных средних значений будут принадлежать рассчитанному нами доверительному интервалу. да-да, тут просто надо представить это в уме

Если из лекции усвоить разницу между средним ГС и средним выборки, а так же понять, что доверительный интервал строится для выборки, а не для ГС, то ответы в тесте легко определяются.

In [11]:

'''Вычисление 1.96 c помощью scipy'''
from scipy import stats

# 95%
p = 0.95
# так как у нас двухсторонний интервал, сделаем вычисление
alpha = (1-p)/2
# isf - Inverse survival function (inverse of sf) 
print(f'{stats.norm().isf(alpha):.2f} sigma')

1.96 sigma

In [12]:

'''Рассчитайте 99% доверительный интервал для следующего примера: 
среднее = 10, стандартное отклонение = 5, размер выборки = 100
'''
from numpy import sqrt
from scipy import stats

p = 0.99
mean = 10
std = 5
n = 100

se = std/sqrt(n)
alpha = (1-p)/2
sigma = stats.norm().isf(alpha)
сonfidence_interval = mean - sigma*se, mean + sigma*se
print('[%.2f; %.2f]' % сonfidence_interval)

[8.71; 11.29]

Идея статистического вывода¶

Статистическая проверка гипотез¶

p-уровень значимости¶

p-уровень значимости - это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет.

Часть 2¶

T-распределение¶

Распределение Стьюдента по сути представляет собой сумму нескольких нормально распределенных случайных величин. Чем больше величин, тем больше верятность, что их сумма будет иметь нормальное распределение. Таким образом, количество суммируемых величин определяет важнейший параметр формы данного распредения - число степеней свободы.

In [13]:

'''График снизу показывает, как меняется форма распределения при увеличение количества степеней свободы.
А также показывает приближение t-распредееления к нормальному по мере увеличения степеней свободы.'''
from scipy.stats import t, norm
import numpy as np
import matplotlib.pyplot as plt


x = np.linspace(-5, 5, 100)
y1, y2, y3 = t.pdf(x, df=1), t.pdf(x, df=3), t.pdf(x, df=10)
y4 = norm.pdf(x)

plt.title('графики t-распредления с разными степенями свободы')
plt.plot(x, y1)
plt.plot(x, y2)
plt.plot(x, y3)
plt.plot(x, y4, 'r:')
plt.legend(('df=1', 'df=3', 'df=10', 'norm'))
plt.show()

График плотности распределения Стьюдента, как и нормального распределения, является симметричным и имеет вид колокола, но с более «тяжёлыми» хвостами.

Подробно про нормальное и t-распредление¶

В видео лекциях говорилось, что мы используем t-распределение в ситуации небольшого объема выборки. Необходимо более подробно пояснить, зачем это нужно.

Вернемся к предельной центральной теореме, мы уже узнали, что если некий признак в генеральной совокупности распределен нормально со средним $\mu$ и стандартным отклонением $\sigma$, и мы будем многократно извлекать выборки одинакового размера n, и для каждой выборки рассчитывать, как далеко выборочное среднее $\bar{X}$ ˉ отклонилось от среднего в генеральной совокупности в единицах стандартной ошибки среднего:

$$\large z = \frac{\bar{X} - \mu}{\frac{\sigma}{\sqrt{n}}}$$

то эта величина z будет иметь стандартное нормальное распределение со средним равным нулю и стандартным отклонением равным единице.

Обратите внимание, что для расчета стандартной ошибки мы используем именно стандартное отклонение в генеральной совокупности - $\sigma$. Ранее мы уже обсуждали, что на практике $\sigma$ нам практически никогда не известна, и для расчета стандартной ошибки мы используем выборочное стандартное отклонение.

Так вот, строго говоря в таком случае распределение отклонения выборочного среднего и среднего в генеральной совокупности, деленного на стандартную ошибку, теперь будет описываться именно при помощи t - распределения.

$$\large t = \frac{\bar{X} - \mu}{\frac{sd}{\sqrt{n}}}$$

таким образом, в случае неизвестной $\sigma$ мы всегда будем иметь дело с t-распределением. На этом этапе вы должны с негодованием спросить меня, почему же мы применяли z-критерий в первом модуле курса, для проверки гипотез, используя выборочное стандартное отклонение?

Мы уже знаем, что при довольно большом объеме выборки (обычно в учебниках приводится правило, n > 30) t-распределение совсем близко подбирается к нормальному распределению:

Поэтому иногда, для простоты расчетов говорится, что если n > 30, то мы будем использовать свойства нормального распределения для наших целей. Строго говоря, это конечно неправильный подход, который часто критикуют. В до компьютерную эпоху этому было некоторое объяснение, чтобы не рассчитывать для каждого n больше 30 соответствующее критическое значение t - распределения, статистики как бы округляли результат и использовали нормальное распределение для этих целей. Сегодня, конечно, с этим больше никаких проблем нет, и все статистические программы, разумеется, без труда рассчитают все необходимые показатели для t - распределения с любым числом степеней свободы. Действительно при выборках очень большого объема t - распределение практически не будет отличаться от нормального, однако, хоть и очень малые но различия все равно будут.

Поэтому, правильнее будет сказать, что мы используем t - распределение не потому что у нас маленькие выборки, а потому что мы не знаем стандартное отклонение в генеральной совокупности. Поэтому в дальнейшем мы всегда будем использовать t - распределение для проверки гипотез, если нам неизвестно стандартное отклонение в генеральной совокупности, необходимое для расчета стандартной ошибки, даже если объем выборки больше 30.

5.Примеры¶

In [14]:

'''На выборке в 15 наблюдений при помощи одновыборочного t-теста
проверяется нулевая гипотеза: μ=10 
и рассчитанное t-значение равняется -2 (t = -2), то p-уровень значимости  (двусторонний) равен:
'''
from scipy import stats

t = -2
n = 15
df = n - 1

p = 2 * stats.t.sf(abs(t), df)
print(f'p = {p:.3f}')

p = 0.065

Сравнение двух средних. t-критерий Стьюдента¶

t-критерий Стьюдента — общее название для статистических тестов, в которых статистика критерия имеет распределение Стьюдента. Наиболее часто t-критерии применяются для проверки равенства средних значений в двух выборках. Нулевая гипотеза предполагает, что средние равны (отрицание этого предположения называют гипотезой сдвига). Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение.

$$ t = \frac{\bar{X_1} - \bar{X_2}}{se}$$$$ se = \sqrt{\frac{sd_1^2}{n_1} + \frac{sd_2^2}{n_2}} $$

Откуда берётся такая формула $se$?:

$$ (se_1)^2 = (\frac{sd_1}{\sqrt{n_1}})^2 = \frac{sd_1^2}{n_1} $$

То есть:

$$ se = \sqrt{\frac{sd_1^2}{n_1} + \frac{sd_2^2}{n_2}} = \sqrt{se_1^2 + se_2^2} $$

причем ответ на вопрос, почему верно это равенство, кроется в свойстве дисперсии: дисперсия суммы независимых случайных величин равна сумме их дисперсий. а отклонение - это корень из дисперсии. отсюда ваша последняя формула

Примеры применения t-критерий Стьюдента¶

Пример 1. Первая выборка — это пациенты, которых лечили препаратом А. Вторая выборка — пациенты, которых лечили препаратом Б. Значения в выборках — это некоторая характеристика эффективности лечения (уровень метаболита в крови, температура через три дня после начала лечения, срок выздоровления, число койко-дней, и т.д.) Требуется выяснить, имеется ли значимое различие эффективности препаратов А и Б, или различия являются чисто случайными и объясняются «естественной» дисперсией выбранной характеристики.

Пример 2. Первая выборка — это значения некоторой характеристики состояния пациентов, записанные до лечения. Вторая выборка — это значения той же характеристики состояния тех же пациентов, записанные после лечения. Объёмы обеих выборок обязаны совпадать; более того, порядок элементов (в данном случае пациентов) в выборках также обязан совпадать. Такие выборки называются связными. Требуется выяснить, имеется ли значимое отличие в состоянии пациентов до и после лечения, или различия чисто случайны.

Пример 3. Первая выборка — это поля, обработанные агротехническим методом А. Вторая выборка — поля, обработанные агротехническим методом Б. Значения в выборках — это урожайность. Требуется выяснить, является ли один из методов эффективнее другого, или различия урожайности обусловлены случайными факторами.

Пример 4. Первая выборка — это дни, когда в супермаркете проходила промо-акция типа А (красные ценники со скидкой). Вторая выборка — дни промо-акции типа Б (каждая пятая пачка бесплатно). Значения в выборках — это показатель эффективности промо-акции (объём продаж, либо выручка в рублях). Требуется выяснить, какой из типов промо-акции более эффективен.

6. Примеры¶

In [15]:

import pandas as pd
from scipy.stats import t
import matplotlib.pyplot as plt
import numpy as np

array1 = np.array([84.7, 105.0, 98.9, 97.9, 108.7, 81.3, 99.4, 89.4, 93.0,
                   119.3, 99.2, 99.4, 97.1, 112.4, 99.8, 94.7, 114.0, 95.1, 115.5, 111.5])
array2 = np.array([57.2, 68.6, 104.4, 95.1, 89.9, 70.8, 83.5, 60.1, 75.7,
                   102.0, 69.0, 79.6, 68.9, 98.6, 76.0, 74.8, 56.0, 55.6, 69.4, 59.5])

# считаем количество элементов, среднее, стандартное отклонение и стандартную ошибку
df = pd.DataFrame({'Выборка1':array1, 'Выборка2':array2}).agg(['mean','std','count','sem']).transpose()
df.columns = ['Mx','SD','N','SE']

# рассчитываем 95% интервал отклонения среднего
p = 0.95
K = t.ppf((1 + p)/2, df['Mx']-1)
df['interval'] = K * df['SE']

df

Out[15]:

	Mx	SD	N	SE	interval
Выборка1	100.815	10.246503	20.0	2.291188	4.545754
Выборка2	75.735	15.458102	20.0	3.456537	6.886174

In [16]:

#строим графики, boxplot из изначальных данных array1, array2,  доверительные интервалы из датафрейма df
fig, (ax1, ax2) = plt.subplots(nrows=1, ncols=2, figsize=(14, 9))

# график boxplot
bplot1 = ax1.boxplot([array1, array2],
                     vert=True,  # создаем вертикальные боксы
                     patch_artist=True, # для красоты заполним цветом боксы квантилей
                     labels=['Выборка1', 'Выборка2']) # используется для задания значений выборок в случае с boxplot

# график доверительных интервалов
bplot2 = ax2.errorbar(x=df.index, y=df['Mx'], yerr=df['interval'],\
                      color="black", capsize=3, marker="s", markersize=4, mfc="red", mec="black", fmt ='o')

# раскрасим boxplot  
colors = ['pink', 'lightgreen']
for patch, color in zip(bplot1['boxes'], colors):
    patch.set_facecolor(color)
    
# добавим общие для каждого из графиков данные
for ax in [ax1, ax2]:
    ax.yaxis.grid(True)
    ax.set_title('Температура плавления ДНК двух типов')
    ax.set_xlabel('Сравнение двух выборок')
    ax.set_ylabel('Температура F')
    
plt.show()

Задача¶

Рассчитайте доверительный интервал основываясь на знании t - распределения для среднего значения температуры плавления ДНК у первого вида:

$$ \bar{X}=89,9\quad sd=11,3\quad n=20 $$

In [17]:

from scipy import stats
from math import sqrt

mean = 89.9
sd = 11.3
n = 20
# степень свободы
df = n - 1
# 95% доверительный интервал
p = 0.95
alpha = 1-p
# стандартная ошибка
se = sd/sqrt(n)

# ppf - Percent point function
# делим на два, так как по умолчанию функция считает для одного конца, а нам надо для двух
t_value = stats.t(df).ppf(1-(alpha/2))

# доверительный интервал 
сonfidence_interval = (mean-t_value*se, mean+t_value*se)
print('[%.2f; %.2f]' % сonfidence_interval)

[84.61; 95.19]

Первые премии Оскар за лучшую мужскую и женскую роль были вручены в 1929. Данные гистограммы демонстрируют распределение возраста победителей с 1929 по 2014 год (100 мужчин, 100 женщин). Используя t - критерий проверьте, можно ли считать наблюдаемые различия в возрасте между лучшими актрисами и актерами статистически достоверными.

Средний возраст мужчин равен 45, sd = 9.

Средний возраст женщин равен 34, sd = 10.

In [18]:

from scipy.stats import t
from numpy import sqrt

mean_m, mean_f = 45, 34
sd_m, sd_f = 9, 10
N = 100

se = sqrt((sd_m ** 2)/N + (sd_f ** 2)/N)
t_value = (mean_m - mean_f)/se

p = t.sf(t_value, N-2)
print(f'p={p}')
if p >= 0.05:
    print('Мы НЕ можем отклонить нулевую гипотезу')
else:
    print('Мы можем отклонить нулевую гипотезу')

p=5.328933875539173e-13
Мы можем отклонить нулевую гипотезу

Проверка распределения на нормальность¶

QQ-plot¶

Эту тему пока сам не понял, так что инфы мало((

7.Примеры¶

In [19]:

import numpy as np 
import scipy.stats as stats
import matplotlib.pyplot as plt

plt.rcParams['figure.figsize'] = [12, 6]

mu, sigma = 10, 4
n = 1000 # с ростом числа точек в распределении qq-plot стремится к прямой
sequence = np.random.normal(mu, sigma, n)


fig, (ax1, ax2) = plt.subplots(1, 2)
fig.suptitle('QQ Plot', fontsize=18)

# Q-Q Plot graph
stats.probplot(sequence, dist="norm", plot=ax1)
ax1.set_title("Normal Q-Q Plot")

# normal distribution histogram + distribution
count, bins, _ = ax2.hist(sequence, 25, density=True)
p_x = 1/(sigma * np.sqrt(2 * np.pi)) * np.exp( - (bins - mu)**2 / (2 * sigma**2) )
ax2.plot(bins, p_x, color='r')
 

plt.show()

Однофакторный дисперсионный анализ¶

Рассмотренный ранее t-критерий Стьюдента (равно как и его непараметрические аналоги) предназначен для сравнения исключительно двух совокупностей. В таком случае мы можем применять однофакторный дисперсионный анализ. Та переменная, которая будет разделять наших испытуемых или наблюдения на группы (номинативная переменная с нескольким градациями) называется независимой переменной. А та количественная переменная, по степени выраженности которой мы сравниваем группы, называется зависимая переменная.

$$ SS_{total} = \sum_{j=1}^{p}{\sum_{i=1}^{n_j}{(x_{ij} - \bar{x})^2}} = SS_{between} + SS_{within} $$$$ SS_{between} = \sum_{j=1}^{p}{n_j{(\bar{x}_j - \bar{x})^2}} $$$$ SS_{within} = \sum_{j=1}^{p}{\sum_{i=1}^{n_j}{(x_{ij} - \bar{x}_j)^2}} $$

In [20]:

from scipy import stats
import pandas as pd

# Выборки которые надо сравнить
data = pd.DataFrame({
           'a': [3, 1, 2],
           'b': [5, 3, 4],
           'c': [7, 6, 5]
          })
data.boxplot()
print('Нулевая гипотеза:', '='.join(data))
print('Альтернативная гипотеза:', f'!({"=".join(data)})')
# общая средняя
grand_mean = data.values.flatten().mean()
# отклонение групповых средний от общей средней
ssb = sum(data[group].size * (group_mean - grand_mean)**2  for group, group_mean in data.mean().items())
# отклонения значений в внутри группы от средней группы
ssw = sum(sum((x - group_mean)**2 for x in data[group]) for group, group_mean in data.mean().items())

groups = data.shape[1]
dfb = groups - 1
dfw = data.size - groups
# межгрупповой средний квадрат  
mssb = ssb/dfb
# внутригрупповой средний квадрат
mssw = ssw/dfw

f_value = mssb/mssw

p = stats.f.sf(f_value, dfb, dfw)
print('Результат:')
if p < 0.05:
    print('отклоняем нулевую гипотезу')
else:
    print('НЕ отклоняем нулевую гипотезу')

Нулевая гипотеза: a=b=c
Альтернативная гипотеза: !(a=b=c)
Результат:
отклоняем нулевую гипотезу

Множественные сравнения в ANOVA¶

В отличие от t-критерия, позволяет сравнивать средние значения трёх и более групп. Разработан Р. Фишером для анализа результатов экспериментальных исследований. В литературе также встречается обозначение ANOVA (от англ. ANalysis Of VAriance) - дисперсионный анализ

почему мы не можем применить t-критерий для более двух выборок¶

применяя его попарно к каждой выбрке

Чтобы выяснить это, сделаем эксперемент.

In [21]:

import numpy as np
from numpy import random
import matplotlib.pyplot as plt
from scipy.stats import t


def pair_t(samples, alpha):
    '''Парный t-критерий, если все выборки равны, возвращает True'''
    n_samples = samples.shape[0]
    # https://ru.wikipedia.org/wiki/Сочетание    
    n_combinations = n_samples*(n_samples - 1)//2
    result = np.zeros(n_combinations, dtype=bool)
    k = 0
    for i in range(n_samples):
        for j in range(i+1, n_samples):
            N = samples[i].size
            std_err = np.sqrt((samples[i].std()**2)/N + (samples[j].std()**2)/N)
            t_value = (samples[i].mean() + samples[j].mean())/std_err
            p = t.sf(t_value, N-2)
            result[k] = p >= alpha
            k += 1
    return np.all(result)

In [22]:

def pair_t_test(repeat, n_samples, sample_size, ax, alpha=0.05):
    '''
    функция показывает, сколько у нас будет ложных результатов, при парном сравнение множества выборок
    с помощью t-критерия
    
    repeat, n_samples, sample_size = количество повторов, количество выборок в каждом повторе, размер выборки
    
    ax - для рисования
    alpha = (1 - (p-уровень значимости))
    '''
    result = np.zeros(repeat, dtype=bool)
    for i in range(repeat):
        samples = random.randn(n_samples, sample_size)
        result[i] = pair_t(samples, alpha)
    
    unique, counts = np.unique(result, return_counts=True)
    percentage = counts/result.size
    ax.pie(percentage, normalize=False, labels=unique, autopct='%.0f%%')

In [23]:

fig, axs = plt.subplots(ncols=4, figsize=(20, 4))
n_samples = [2, 4, 8, 16]
fig.suptitle('Процент ошибок при попарном сравнение выборок t-критерием')

for n, ax in zip(n_samples, axs):
    pair_t_test(1000, n, 100, ax)
    ax.set_title(f'{n} samples')
    

Как мы и ожидаем, степень ошибки равна 5%, при сравнение двух выборок из одной ГС с помощью t-критерия с p-уровнем значимости 95%. Если мы возмём 4 выборки, и сравним их попарно, то ошибка возрастёт в 4 раза до 20%. При 8 выборок, наша ошибка возрасла почти в 9 раз до 46%. 16 выборок дают увеличение ошибки до 80% ( в 16 раз), что совершенно неприемлемо.

In [24]:

fig, axs = plt.subplots(ncols=4, figsize=(20, 4))
n_samples = [2, 4, 8, 16]
fig.suptitle('Процент ошибок при попарном сравнение выборок t-критерием с корректировкой уровня значимости')

for n, ax in zip(n_samples, axs):
    alpha = 0.05/((n*(n-1))/2)
    pair_t_test(1000, n, 100, ax, alpha)
    ax.set_title(f'{n} samples')

Однако в данном случае эта будет арх-консервативная корректировавка, которая имеет меньше вероятность найти реальные значения. По сути мы уменьшаем шанс получить ошибку I рода, но увеличиваем шанс на ошибку II рода.

Ошибки первого и второго рода¶

Многофакторный ANOVA¶

Часть 3¶

Корреляция¶

Ковариация¶

(ко - совместная, вариация - изменчивость). Мера линейной зависимости двух случайных величин.

Если ковариация положительна, то с ростом значений одной случайной величины, значения второй имеют тенденцию возрастать, а если знак отрицательный — то убывать.

$$ cov(X, Y) = \frac{\sum{(x_i - \bar{x})(y_i - \bar{x})}}{N - 1} $$

где N - количество случайных величин, а единица - количество степеней свободы.

Однако только по абсолютному значению ковариации нельзя судить о том, насколько сильно величины взаимосвязаны, так как масштаб ковариации зависит от их дисперсий. Значение ковариации можно нормировать, поделив её на произведение среднеквадратических отклонений (квадратных корней из дисперсий) случайных величин. Полученная величина называется коэффициентом корреляции Пирсона, который всегда находится в интервале от −1 до 1:

$$ r(x, y) = \frac{cov(x, y)}{\sigma_x\sigma_y}$$

Подробнее про формулу корреляции¶

Давайте остановимся на формуле коэффициента корреляции, которую мы получили: $$ r(x, y) = \frac{cov(x, y)}{\sigma_x\sigma_y}$$ запишем формулу чуть подробнее и выполним возможные преобразования:

$$ r(x, y) = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{(N - 1)\sqrt{\sum{\frac{(x_i - \bar{x})^2}{N-1}}}\sqrt{\sum{\frac{(y_i - \bar{y})^2}{N-1}}}} $$

теперь вынесем 1/ (N - 1) из под корней

$$ r(x, y) = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{(N - 1)\frac{1}{(N-1)}\sqrt{\sum{(x_i - \bar{x})^2}}\sqrt{\sum{(y_i - \bar{y})^2}}} $$

и сократим (N - 1)

$$ r(x, y) = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{\sqrt{\sum{(x_i - \bar{x})^2}}\sqrt{\sum{(y_i - \bar{y})^2}}} $$

таким образом, мы сократили N - 1 в знаменателе и получили финальную формулу для коэффициента корреляции, которую вы часто сможете встретить в учебниках:

$$ r(x, y) = \frac{\sum{(x_i - \bar{x})(y_i - \bar{y})}}{\sqrt{\sum{(x_i - \bar{x})^2}\sum{(y_i - \bar{y})^2}}} $$

Примеры 3.1¶

In [25]:

'''Демонстрация работы ковариации и корреляции'''
import numpy as np
import random as r

def cov(x, y):
    assert x.size == y.size
    return ((x - x.mean()) * (y - y.mean())).sum()/(x.size - 1)

def cor(x, y):
    return cov(x, y)/(np.std(x, ddof=1)*np.std(y, ddof=1))

# функция имитирущая случаные факторы
# р - настолько существенным будет случайный фактор
def randomize(arr, p):
    alpha = np.max(arr) - np.min(arr)
    res = np.zeros(arr.shape)
    for i, v in enumerate(arr):
        sign = 1 if r.choice([True, False]) else -1
        res[i] = v + sign*alpha*r.random()*p
    return res

In [26]:

x = np.array(range(30))
y = randomize(x, 0.1)
y1 = randomize(x, 0.5)
y2 = randomize(x, 1)

In [27]:

import matplotlib.pyplot as plt

fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(16, 3))
ax1.scatter(x, y)
ax2.scatter(x, y1)
ax3.scatter(x, y2)
ax1.set_title('высокая корреляция')
ax2.set_title('средняя корреляция')
ax3.set_title('низкая корреляция')
plt.show()

In [28]:

print(f'''
cov1: {cov(x, y):.2f}
cov2: {cov(x, y1):.2f}
cov3: {cov(x, y2):.2f}

cor1: {cor(x, y):.2f}
cor2: {cor(x, y1):.2f}
cor3: {cor(x, y2):.2f}
''')

cov1: 75.61
cov2: 77.81
cov3: 86.23

cor1: 0.98
cor2: 0.75
cor3: 0.51

Регрессия с одной независимой переменной¶

В этой и следующих главах мы научимся работать с одномерным регрессионным анализом, который позволяет проверять гипотезы о взаимосвязи одной количественной зависимой переменной и нескольких независимых.

Сначала мы познакомимся с самым простым вариантом - простой линейной регрессией, при помощи которой можно исследовать взаимосвязь двух переменных. Затем перейдем к множественной регрессии с несколькими независимыми переменными.

Линейная регрессия (англ. Linear regression) — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной $y$ от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) $x$ с линейной функцией зависимости.

В общем виде функция линейной регрессии выглядит как:

$$ y = b_0 + b_1x $$

$b_0$ - intercept значение пересечения линии с осью Y

$b_1$ - slope задаёт наклон линии регрессии

строят регрессионную прямую методом наименьших квадратов (МНК)

МНК - это способ нахождения оптимальных параметров линейной регресссии ($b_0$, $b_1$), таких, что сумма квадратов ошибок (остатков) была минимальная.

Расчёт параметров идёт по таким формулам:

$$ b_1 = \frac{sd_y}{sd_x}r_{xy} $$$$ b_0 = \bar{Y} - b_1\bar{X} $$

In [29]:

'''Демонстрация МНК'''
b1 = y1.std()/x.std()*cor(x, y1)
b0 = y1.mean() - b1*x.mean()
f = lambda x: b0 + b1*x
y_pred = f(x)
plt.scatter(x, y1)
plt.plot(x, y_pred, color='r')
plt.show()

Гипотеза о значимости взаимосвязи и коэффициент детерминации¶

Условия применения линейной регрессии с одним предиктором¶

Применение регрессионного анализа и интерпретация результатов¶

In [30]:

''''''
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import numpy as np

df = pd.read_csv('data/states.csv')
df.head()

Out[30]:

	state	metro_res	white	hs_grad	poverty	female_house
0	Alabama	55.4	71.3	79.9	14.6	14.2
1	Alaska	65.6	70.8	90.6	8.3	10.8
2	Arizona	88.2	87.7	83.8	13.3	11.1
3	Arkansas	52.5	81.0	80.9	18.0	12.1
4	California	94.4	77.5	81.1	12.8	12.6

Есть данные по штатам с различными значениями:

metro_res - процент населения живущие в столице
white - процент белого населения
hs_grad - процент людей со образованием
poverty - уровень бедности
female_house - процент домов, где есть домохозяйки

Исследуем связь уровня образования и бедности, где бедность будет ЗП, а уровень образования НП.

Первое, что нам необходимо сделать, это построить линейную модель, которая наилучшим образом будет описывать наши данные.

$$ \hat{y} = b_0 + b_1x $$

Далле, построив нашу модель, нам надо узнать, насколько хорошо наша объясняет ЗП, для этого найдём коэфицент детерминации $R^2$

Проверим нулевую гипотезу: $$ b_1 = 0 : H0$$

Третья наша задача, это задача предсказания, по данным НП мы хотим предсказать ЗП.

In [31]:

sns.jointplot(x='hs_grad', y='poverty', data=df, kind='reg', color='m')

Out[31]:

<seaborn.axisgrid.JointGrid at 0x1c37eb775e0>

In [32]:

df_descr = df.describe().transpose()
df_descr

Out[32]:

	count	mean	std	min	25%	50%	75%	max
metro_res	51.0	72.249020	15.275894	38.2	60.80	71.6	86.80	100.0
white	51.0	81.719608	13.897223	25.9	76.80	85.4	90.25	97.1
hs_grad	51.0	86.011765	3.725998	77.2	83.30	86.9	88.70	92.1
poverty	51.0	11.349020	3.099185	5.6	9.25	10.6	13.40	18.0
female_house	51.0	11.633333	2.356155	7.8	9.55	11.8	12.65	18.9

In [33]:

'''Построим модель'''
from scipy.stats import linregress

slope, intercept, r, p, std_err =  linregress(df['hs_grad'], df['poverty'])

x = np.linspace(75, 100)

reg = lambda x: intercept + slope*x
plt.scatter(x='hs_grad', y='poverty', data=df, label='data')
plt.xlabel('hs_grad %')
plt.ylabel('poverty %')
plt.title('Linear Regression')
plt.plot(x, reg(x), color='r', label='fitted line')
plt.legend()
plt.show()

In [34]:

print(f'''
slope = {slope:.2f}
intercept = {intercept:.2f}
r = {r:.2f}
r squared = {(r ** 2):.2f}
p = {p:.5f}
std_err = {std_err:.3f}
''')

slope = -0.62
intercept = 64.78
r = -0.75
r squared = 0.56
p = 0.00000
std_err = 0.079

Задача предсказания значений зависимой переменной¶

Регрессионный анализ с несколькими независимыми переменными¶

Множественная регрессия (Multiple Regression)¶

Множественная регрессия позволяет исследовать влияние сразу нескольких независимых переменных на одну зависиммую.

Требования к данным¶

линейная зависимость переменных
нормальное распредление остатков
гомоскедастичность данных
проверка на мультиколлиарность
нормальное распределение переменных (желательно)

Пример расчёта и визуализации множественной регрессии¶

In [35]:

import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
import numpy as np
import statsmodels.formula.api as smf

df = pd.read_csv('data/states.csv')

# Построим плоскость предсказания
lm = smf.ols(formula='poverty ~ white + hs_grad', data=df).fit()
mesh_size = 1.0
margin = 2.0
x_min, x_max = df.white.min()- margin, df.white.max() + margin
y_min, y_max = df.hs_grad.min()- margin, df.hs_grad.max() + margin
z_pred = lambda x, y: lm.params.white * x  + lm.params.hs_grad * y + lm.params.Intercept
x_range = np.arange(x_min, x_max, mesh_size)
y_range = np.arange(y_min, y_max, mesh_size)
z_range = np.array([[z_pred(x, y) for x in x_range] for y in y_range])

# какие значения выше предсказания, а какие ниже
df['poverty_pred'] = np.array([poverty >= z_pred(df.white[i], df.hs_grad[i]) for i, poverty in df.poverty.items()])

# составим график
fig = px.scatter_3d(df, x='white', y='hs_grad', z='poverty',
                    color='poverty_pred', color_discrete_sequence=['red', 'green'],
                   title='зависиость процента белого населения и уровня образования на бедность населения')
fig.update_traces(marker=dict(size=3))
fig.add_traces(go.Surface(x=x_range,y=y_range, z=z_range, name='prediction', opacity=0.8))
fig.show()

** сверху должен быть объёмный график, но если его не видно, запустите этот код у себя на компе

In [ ]:

Выбор наилучшей модели¶

Классификация: логистическая регрессия и кластерный анализ¶

Полезные ссылки¶

https://gallery.shinyapps.io/dist_calc/
- сайт где можно визуализировать различные распределения и вести подсчёты