
© Copyright Franck CHEVRIER 2019-2022 https://www.python-lycee.com.
Les activités partagées sur Capytale sont sous licence Creative Commons.
Pour exécuter une saisie Python, sélectionner la cellule et valider avec SHIFT+Entrée.
Méthode de Héron (Corrigé)
Approximation et encadrement d'une racine carrée
1. Présentation géométrique de la méthode¶
Le but de cette activité est d'obtenir des valeurs approchées d'une expression $\sqrt{p}$ à l'aide d'opérations élémentaires.
Dans cette activité, on considérera que $p$ est un entier naturel non nul.
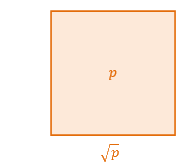
Par définition, $\sqrt{p}$ est la longueur du côté d'un carré dont l'aire vaut $p$.
L'idée est d'approcher géométriquement ce carré à l'aide de rectangles dont les aires valent $p$ et tels que l'on puisse exprimer les longueurs de leurs côtés.
- On démarre au rang $0$ avec un rectangle de dimensions $a_0=p$ et $b_0=1$, dont l'aire vaut $p$.
- Au rang $1$, on construit un rectangle de dimensions $a_1$ et $b_1$ telles que :
- $a_1$ est la moyenne des longueurs $a_0$ et $b_0$ (dimensions du rectangle précédent);
- $b_1$ est choisi de telle sorte que l'aire du rectangle soit égale à $p$.

1.1. $\displaystyle a_1=\frac{a_0+b_0}{2} \;$ ; $a_1\times b_1=p$ donc $\displaystyle b_1=\frac{p}{a_1}$.
Ensuite :1.2. Activer la figure dynamique ci-dessous, qui permet d'observer la construction géométrique des premiers rectangles.On reprend la méthode pour construire les rectangles suivants, en utilisant à chaque étape les dimensions du rectangle précédent.
$\quad$On observera en particulier que les rectangles semblent "se rapprocher" d'un carré d'aire $p$.
$\quad$Il semble donc que les termes $a_n$ pourraient fournir des approximations de la longueur du côté d'un carré d'aire $p$, c'est à dire de $\sqrt{p}$.
#Sélectionner cette zone puis SHIFT+ENTREE
from IPython.display import HTML ; HTML("""<iframe scrolling="no" title="Héron" src="https://www.geogebra.org/material/iframe/id/krfmqjjr/width/1067/height/608/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="1067px" height="608px" style="border:0px;"> </iframe>""")

2. Étude mathématique et algorithmique¶
2.1. Justifier que $\forall n\in \mathbb{N}\;;\;\displaystyle a_{n+1}=\frac{a_n+b_n}{2}\;$ et $\;\forall n\in \mathbb{N}\;;\;\;\displaystyle b_{n}=\frac{p}{a_{n}}$.
2.2. En déduire que la suite $(a_n)_{n \geq 0}$ vérifie :
$ \begin{Bmatrix}
a_0=p \\
\forall n\in \mathbb{N} \;;\; a_{n+1} = \displaystyle \frac{1}{2} \left( a_n+\frac{p}{a_n} \right) \end{Bmatrix}$
2.1. $a_{n+1}$ étant par construction la moyenne de $a_n$ et $b_n$, on a $\displaystyle a_{n+1}=\frac{a_n+b_n}{2} \;$.
$\quad\;\;$Pour tout $n\in\mathbb{N}$, l'aire du rectangle de rang $n$ a pour aire $a_n\times b_n = p$ donc $\displaystyle b_{n}=\frac{p}{a_{n}}$.
2.2. $a_0=p$ d'après l'énoncé (construction du rectangle de rang $0$).
$\displaystyle \quad\;\; a_{n+1}=\frac{a_n+b_n}{2}=\frac{a_n+\frac{p}{a_{n}}}{2}=\frac{1}{2}\left( a_n+\frac{p}{a_n} \right) \;$
$\quad\quad \begin{Bmatrix} a_0=13 \\ \forall n\in \mathbb{N} \;;\; a_{n+1} = \displaystyle \frac{1}{2} \left( a_n+\frac{13}{a_n} \right) \end{Bmatrix}$
$\quad\;$On souhaite implémenter en Python la suite $(a_n)_{n\geq0}$.
$\quad\;\;$a. Écrire une fonction Python Heron qui reçoit n en argument et qui renvoie la valeur de $a_n$.
# Écrire ici la fonction Heron
def Heron(n):
a = 13
for k in range(n):
a = 1/2*(a+13/a)
return a
$\quad\quad\;\;$Vérifier la cohérence du résultat avec la figure dynamique fournie précédemment dans la question 1.2.
# Effectuer ici l'appel à la fonction Heron
Heron(3)
3.6820276497695854
$\quad\;$b. Justifier que $\displaystyle \;\forall n\in \mathbb{N} \;;\; a_{n+1}-a_n = \frac{p-a_n^2}{2a_n}$ et en déduire que la suite $(a_n)_{n \geq 0}$ est décroissante.
$\quad\;$c. En déduire que la suite $(a_n)_{n \geq 0}$ admet une limite finie, que l'on notera $L$.
Le membre de droite est un carré donc est positif, et on en déduit que $\forall n\in \mathbb{N}\;; a_{n+1}^2-p \geq 0$, ce qui donne $a_{n+1}\geq\sqrt{p}$.
De plus, on a aussi $a_0=p=\sqrt{p}^2\geq\sqrt{p}$ car $p\in \mathbb{N}^*$.
b. $\displaystyle \;\forall n\in \mathbb{N} \;;\; a_{n+1}-a_n = \displaystyle \frac{1}{2} \left( a_n+\frac{p}{a_n} \right)-a_n = \frac{1}{2} \left( a_n+\frac{p}{a_n}-2a_n \right) = \frac{1}{2} \left( \frac{p}{a_n}-a_n \right) = \frac{1}{2} \left( \frac{p-a_n^2}{a_n} \right)=\frac{p-a_n^2}{2a_n}$
$\;\forall n\in \mathbb{N} \;;\; a_n \geq \sqrt{p}$ donc $a_n^2 \geq p$ donc $p-a_n^2 \leq 0$, d'où on déduit $a_{n+1}-a_n \leq 0$, c'est à dire $a_{n+1}\leq a_n$.
$(a_n)_{n \geq 0}$ est bien décroissante.
c. La suite $(a_n)_{n \geq 0}$ étant décroissante et minorée par $\sqrt{p}$, on en déduit qu'elle est convergente, et on note $L$ sa limite.
En passant à la limite quand $n$ tend vers $+\infty$ dans $a_{n+1} = \displaystyle \frac{1}{2} \left( a_n+\frac{p}{a_n} \right)$, on obtient $L = \displaystyle \frac{1}{2} \left( L+\frac{p}{L} \right)$
On résout alors l'équation :
$L = \displaystyle \frac{1}{2} \left( L+\frac{p}{L} \right)$
$\displaystyle \Leftrightarrow L - \frac{1}{2} \left( L+\frac{p}{L} \right) = 0$
$\displaystyle \Leftrightarrow \frac{1}{2} L - \frac{p}{2L} = 0$
$\displaystyle \Leftrightarrow \frac{L^2-p}{2L} = 0$
$\displaystyle \Leftrightarrow L^2-p = 0$
$\displaystyle \Leftrightarrow (L-\sqrt{p})(L+\sqrt{p}) = 0$
$\displaystyle \Leftrightarrow L \in \left\{ -\sqrt{p} ; \sqrt{p} \right\}$
et comme $L \geq 0$ (limite d'une suite à termes positifs), on en déduit que $L = \sqrt{p}$.
2.6.a. Modifier la fonction Python Heron écrite à la question 2.3.a de telle sorte que :
- la fonction reçoit deux arguments p et n ;
- la fonction renvoie la valeur de $a_n$ dans le cas général, où $a_0=p$.
# Écrire ici la nouvelle fonction Heron
def Heron(p,n):
a = p
for k in range(n):
a = 1/2*(a+p/a)
return a
$\quad$b. À l'aide d'un appel à la fonction Heron, proposer une valeur approchée de $\sqrt{5}$.
# Effectuer ici l'appel à la fonction Heron
Heron(5,4) # (on a calculé ici le terme de rang 4 de la suite)
2.2360688956433634
3. Encadrement d'une racine carrée¶
On reprend la suite $(a_n)_{n\geq 0}$ définie dans la partie 2, vérifiant : $ \begin{Bmatrix}
a_0=p \\
\forall n\in \mathbb{N} \;;\; a_{n+1} = \displaystyle \frac{1}{2} \left( a_n+\frac{p}{a_n} \right) \end{Bmatrix}$ ,
ainsi que la suite $(b_n)_{n\geq 0}$ vérifiant : $\displaystyle \forall n\in \mathbb{N} \;;\; b_n=\frac{p}{a_n}$.
Info :
Les deux suites $(a_n)_{n\geq0}$ et $(b_n)_{n\geq0}$ étudiées ici sont dites adjacentes.
Il en résulte que $b_n\leq \sqrt{p} \leq a_n$ fournit un encadrement de $\sqrt{p}$ d'amplitude $a_n-b_n$.
- $(a_n)_{n\geq0}$ et $(b_n)_{n\geq0}$ sont respectivement décroissante et croissante ;
- $(a_n)_{n\geq0}$ et $(b_n)_{n\geq0}$ ont la même limite $\sqrt{p}$.
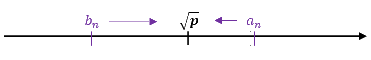
3.1.a. On rappelle que la suite $(a_n)_{n \geq 0}$ est décroissante.
$\quad\quad$Justifier que $(b_n)_{n \geq 0}$ est croissante.
$\quad\;$b. On rappelle que la suite $(a_n)_{n \geq 0}$ a pour limite $\sqrt{p}$.
$\quad\quad$En déduire la limite de la suite $(b_n)_{n \geq 0}$.
$\displaystyle \forall n\in \mathbb{N} \;;\; b_{n+1}-b_n = \frac{p}{a_n+1} - \frac{p}{a_n} = \frac{p(a_n-a_{n+1})}{a_n a_{n+1}}$ et comme $a_{n+1} \leq a_n$, on en déduit que $a_n-a_{n+1}\geq0$ et donc $b_{n+1}-b_n\geq0$.
La suite $(b_n)_{n\geq 0}$ est bien croissante.
3.1.b.
$\displaystyle\lim\limits_{n \to +\infty}{a_n}=\sqrt{p}\;$ donc $\;\displaystyle\lim\limits_{n \to +\infty}{\frac{p}{a_n}}=\frac{p}{\sqrt{p}}=\sqrt{p}\;$ c'est à dire $\;\displaystyle\lim\limits_{n \to +\infty}{b_n}=\sqrt{p}$.
3.2.a. Reprendre et modifier la fonction Python Heron de la question 2.6.a pour qu'elle renvoie les deux valeurs $b_n$ et $a_n$.
# Écrire ici la nouvelle fonction Heron
def Heron(p,n):
a = p
for k in range(n):
a = 1/2*(a+p/a)
b = p/a
return b,a
$\quad$b. Effectuer un appel à cette fonction Heron pour $p=7$ et $n=5$.
$\quad\;\;$Quel encadrement de $\sqrt{7}$ peut-on en déduire ?
# Exécuter ici l'appel à la fonction Heron
Heron(7,5)
(2.6457513110178117, 2.6457513111113693)
3.3.a. Écrire une fonction Python Encadrement_racine qui :
- reçoit en arguments la valeur p et une valeur h strictement positive ;
- renvoie deux valeurs $b_N$ et $a_N$ telles que $a_N-b_N
# Écrire ici la fonction Encadrement_racine
def Encadrement_racine(p,h):
a = p
b = 1
while a-b>=h:
a = 1/2*(a+p/a)
b = p/a
return b,a
$\quad$b. À l'aide d'un appel à la fonction Encadrement_racine, obtenir un encadrement de $\sqrt{720}$ d'amplitude inférieure à $10^{-5}$.
# Exécuter ici l'appel à la fonction Encadrement_racine
Encadrement_racine(720,10**-5)
(26.832815455186363, 26.832816004808592)
4. Contexte historique¶
Dans le tome 1 de son ouvrage "Metrica", Héron d'Alexandrie est amené à évaluer la racine carrée de 720.
Il écrit :
(...)dont voici la traduction :
έπεί ούν αί ψκ ρητήν τήν πλευράν ούκ έχουσι, ληψόμεθα μετά διαφόρου ελάχιστου τήν πλευράν ούτως.
έπεί ό συνεγγίζων τώ ψκ τετράγωνός έστιν ό ψκθ καί πλευράν έ'χει τον κζ, μέρισον τάς ψκ εις τον κζ* γίγνεται κς καί τρίτα δύο’ πρόσθες τάς κζ* γίγνεται νγ τρίτα δύο* τούτων τό ήμισυ* γίγνεται κς L·' γ'* έσται άρα του ψκ ή πλευρά έγγιστα τά κς Δ.' γ'* τά γάρ κς ΙΔ γ' έφ’ έαυτά* γίγνεται ψκ λς'* ώστε τό διάφορον μονάδος έστί μόριον λς'
εάν δέ βουλώμεθα έν έλάσσονι μορίω του λς' τήν διαφοράν γίγνεσθαι, άντί του ψκθ τάξομεν τά νϋν εύρεθέντα ψκ καί λς' καί ταύτά ποιήσαντες εύρήσομεν πολλω έλάττονα του λς' τήν διαφοράν γιγνομένην.
(...)
(...)
Alors, puisque les 720 n’ont pas le côté exprimable, nous prendrons le côté avec une très petite différence ainsi.
Puisque le carré le plus proche de 720 est 729 et qu’il a 27 comme côté, divise les 720 par le 27 : il en résulte 26 ⅔ ; ajoute les 27 : il en résulte 53 ⅔ ; de ceux-ci, la moitié : il en résulte 26 ½ ⅓ : le côté de 720 sera donc 26 ½ ⅓ à très peu près. En effet, les 26 ½ ⅓ par eux-mêmes : il en résulte 720 $1/36$ ; de sorte que la différence est une 36e part d’unité.
Et si nous voulons que la différence se produise par une part plus petite que 1/36, au lieu de 729, nous placerons les 720 $1/36$ maintenant trouvés et, en faisant les mêmes choses, nous trouverons qu’il en résulte une différence inférieure, de beaucoup, à 1/36.
(...)
NB :
- La notation 26 ⅔ signifie $26+\frac{2}{3}$.
- La notation 26 ½ ⅓ signifie $26+\frac{1}{2}+\frac{1}{3}$.
Ayant remarqué que le carré le plus proche de $720$ est $729=27^2$, Héron utilise comme valeur initiale $27$.
En langage mathématique moderne, pour approcher $\sqrt{720}$, Héron utilise donc la suite $(u_n)_{n\geq0}$ définie par :
$ \begin{Bmatrix}
u_0=27 \\
\forall n\in \mathbb{N} \;;\; u_{n+1} = \displaystyle \frac{1}{2} \left( u_n+\frac{720}{u_n} \right) \end{Bmatrix}$
4.1. Vérifier par un calcul fractionnaire exact que la valeur trouvée par Héron pour $u_1$ est correcte.
$u_1 = \displaystyle \frac{1}{2} \left( u_0+\frac{720}{u_0} \right) = \frac{1}{2} \left(27+\frac{720}{27} \right) = \frac{1}{2} \left(27+\frac{80}{3} \right) = \frac{1}{2} \times \frac{27\times3+80}{3} = \frac{161}{6}$.
Or on a $\displaystyle 26+\frac{1}{2}+\frac{1}{3}=\frac{26\times6+3+2}{6}=\frac{161}{6}$, ce qui prouve bien que $\displaystyle u_1=26+\frac{1}{2}+\frac{1}{3}$.
4.2.
$\displaystyle u_1^2=\left( \frac{161}{6} \right)^2 = \frac{161^2}{6^2}=\frac{25921}{36}$
$720\times36=25920$ donc $\displaystyle u_1^2=\frac{25920}{36}+\frac{1}{36}=720+\frac{1}{36}$

© Copyright Franck CHEVRIER 2019-2022 https://www.python-lycee.com.
Les activités partagées sur Capytale sont sous licence Creative Commons.
Dernière modification de l'activité : Juillet 2022