Notebook

En tête general

© Copyright Franck CHEVRIER 2019-2021 https://www.python-lycee.com.
Les activités partagées sur Capytale sont sous licence Creative Commons.

Pour exécuter une saisie Python, sélectionner la cellule et valider avec SHIFT+Entrée.

Algorithme de Dijkstra¶

Le but de l’activité est de découvrir et mettre en oeuvre l'algorithme Dijkstra, permettant d'optimiser un trajet en minimisant distance, temps de parcours ou coût.

1. a. On considère le plan du métro londonien. Les temps de parcours étant donnés en minute, on souhaite minimiser le temps de trajet pour se rendre de la station Westminster (W) à la station King's Cross (K). Suivre la vidéo ci-dessous, qui détaille la modélisation du problème à l'aide d'un graphe et la mise en oeuvre de l'algorithme de Dijkstra sur cet exemple.

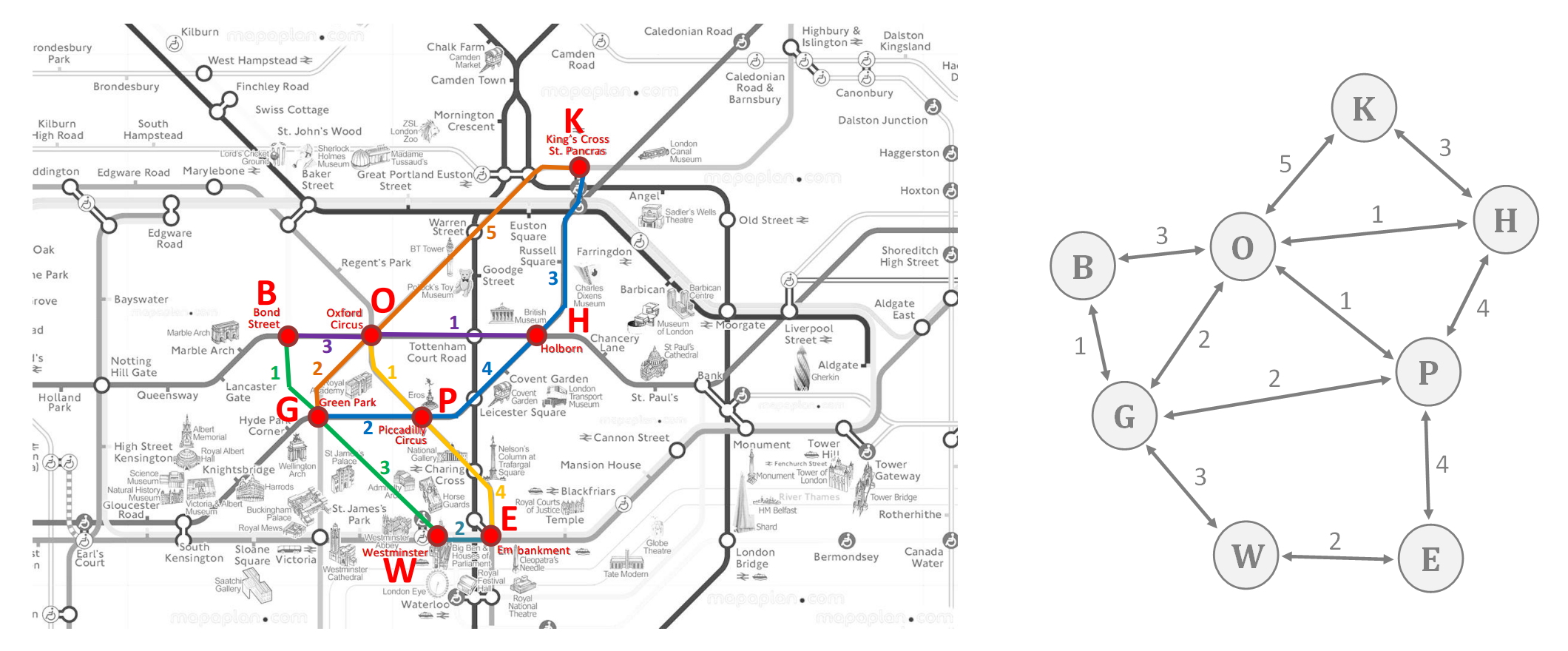
MetroLondres

1. b. On code en Python le graphe précédent à l'aide de la structure G1 ci-dessous. Expliquer brièvement comment sont stockées les informations du graphe dans G1.

Attention : Penser ensuite à exécuter la zone ci-dessous (et les suivantes) avec SHIFT+Entrée.

In [ ]:

G1 = { 'B':{'G':1,'O':3} , 
       'E':{'W':2,'P':4} , 
       'G':{'B':1,'O':2,'P':2,'W':3} , 
       'H':{'P':4,'O':1,'K':3} , 
       'K':{'O':5,'H':3} , 
       'O':{'B':3,'G':2,'P':1,'H':1,'K':5} , 
       'P':{'E':4,'G':2,'O':1,'H':4} , 
       'W':{'G':3,'E':2} 
     }

1. c. La fonction Python Dijkstra ci-dessous permet d'appliquer l'algorithme de Dijkstra. Tester l'appel à la fonction pour G1 afin d'optimiser le trajet de W à K. Vérifier la cohérence avec le résultat obtenu dans la question 1.a.

In [ ]:

def etapes(Graphe,depart,final,s_traites,dist,prec):
    """
    Etapes de l'algorithme de Dijkstra (version récursive)
        
    s_traites:  Liste des sommets déjà traités
    dist:       Distances minimales trouvées pour chaque sommet
    prec:       Indique pour chaque sommet, celui qui le précède dans le trajet le plus court trouvé    
    """    
    #on choisit le sommet à traiter:
    if not dist:
        #si aucune distance n'a été calculée, on choisit depart(et on note 0 comme distance pour le depart)
        s_courant=depart
        dist[s_courant]=0 
    else:
        #sinon on choisit un sommet non encore traité dont la distance calculée est minimale 
        non_traites={ s:dist.get(s,float('inf'))  for s in Graphe if s not in s_traites }
        s_courant=min(non_traites, key=non_traites.get)

    #si le sommet courant est celui à atteindre
    if s_courant==final:
        #construction de la liste des sommets, à rebours
        Chaine=[final]
        while Chaine[-1]!=depart:
            Chaine.append(prec[Chaine[-1]])
        #on renvoie la distance minimale trouvée et la liste des sommets
        Chaine.reverse()
        return dist[final],Chaine

    #on traite tous les voisins du sommet courant
    for voisin in Graphe[s_courant]:
        #on récupère la distance précédemment calculée pour ce voisin (+inf si non atteint)
        dist_voisin_prec=dist.get(voisin,float('+inf'))
        #on calcule la nouvelle distance obtenue

        dist_voisin_new=dist[s_courant]+Graphe[s_courant][voisin]
        #on compare les deux distances et on modifie si nécessaire
        if dist_voisin_new<dist_voisin_prec:
            dist[voisin]=dist_voisin_new
            prec[voisin]=s_courant

    #on ajoute le sommet courant à la liste des sommets traites
    s_traites.append(s_courant)

    #on réitère la méthode pour traiter le sommet suivant
    return etapes(Graphe,depart,final,s_traites,dist,prec)

def Dijkstra(Graphe,depart,final):
    """
    Application de l'algorithme de Dijkstra
    
    Graphe:     Graphe fourni sous forme d'un dictionnaire
    depart:     Sommet initial du trajet cherché 
    final:      Sommet final du trajet cherché
    """  
    return etapes(Graphe,depart,final,[],{},{})
    

In [ ]:

#Appel à la fonction pour le graphe G1, du sommet W au sommet K
Dijkstra(G1,'W','K')

2. a. Le graphe ci-dessous indique les frais de déplacement occasionnés (péage, essence,...) pour un trajet entre deux villes, exprimés en euro. Appliquer l'algorithme de Dijkstra à l'aide d'un tableau pour déterminer le trajet le moins onéreux pour se rendre de Calais à Mulhouse, et indiquer ce coût.

C : Calais
L : Lille
N : Nancy
S : Strasbourg
A : Amiens
T : Troyes
D : Dijon
M : Mulhouse

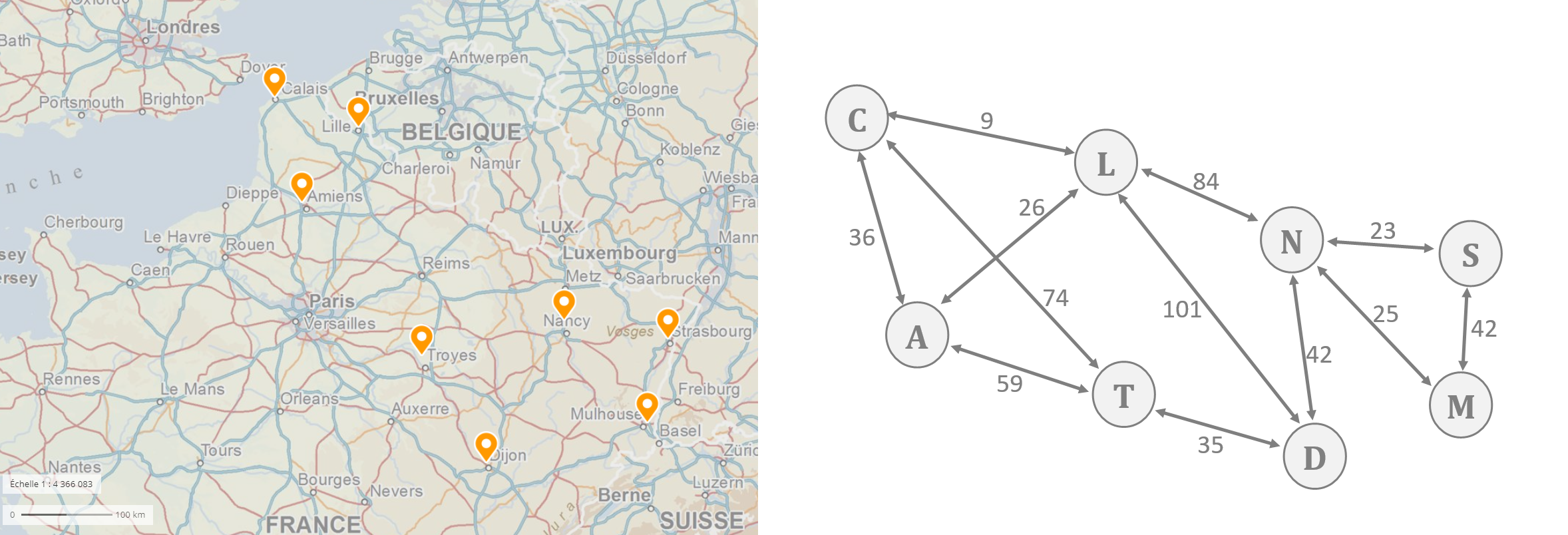
Villes

2. b. Créer une structure Python G2 pour coder ce graphe.

In [ ]:

#Créer la structure G2 (sur le même modèle que G1)

2. c. Effectuer un appel à la fonction Python Dijkstra pour vérifier votre réponse à la question 2.a.

In [ ]:

#Effectuer l'appel à la fonction