Czym jest Machine Learning?¶
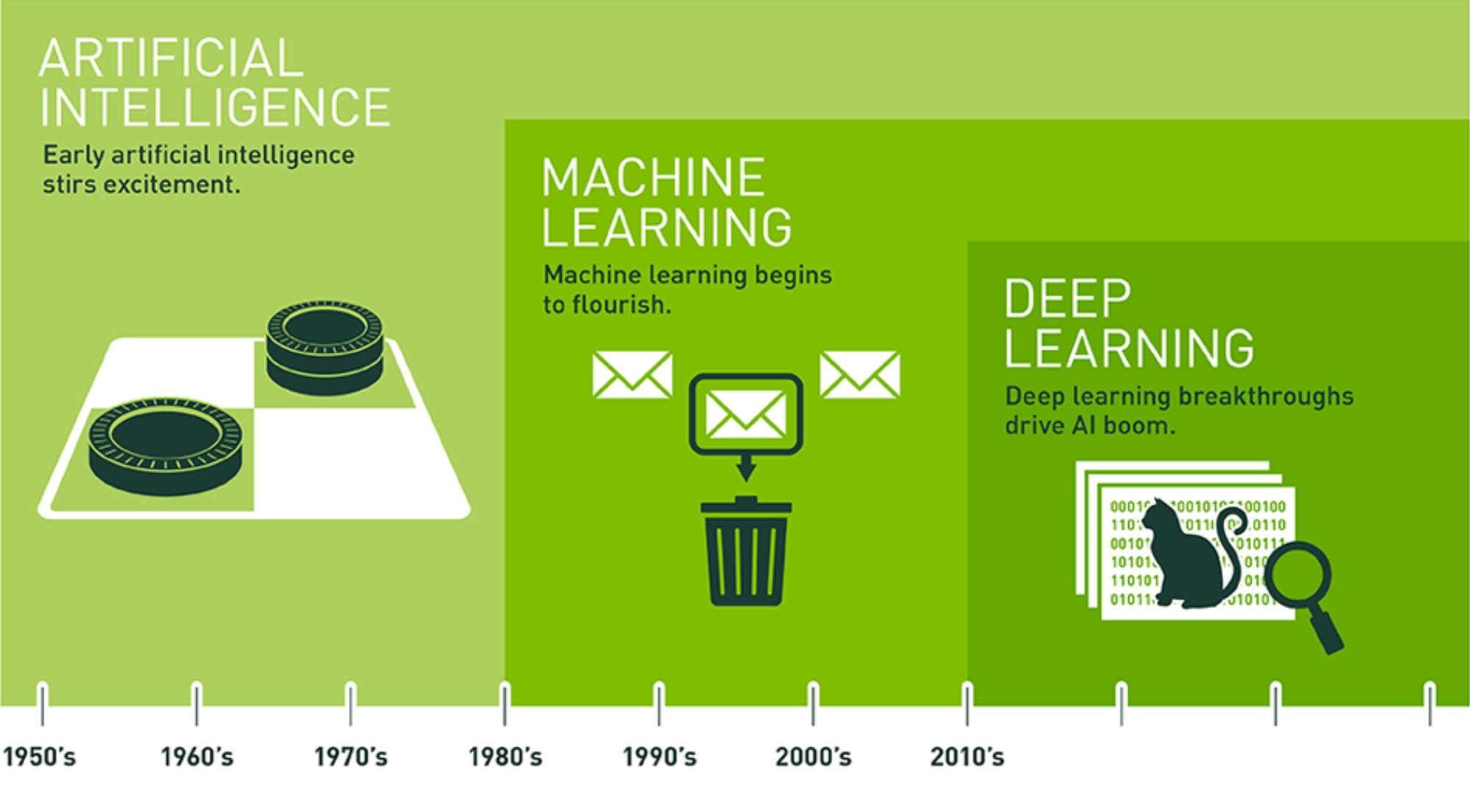
Sztuczna Inteligencja (AI ang. Artificial Intelligence) - to koncepcja według której maszyny są zdolne do wykonywania zadań w sposób inteligentny, a nie zalgorytmizowany w ściśle określony sposób.
Uczenie Maszynowe (ML ang. Machine Learning) -gałąź AI, gdzie do nauki określonego modelu wykorzystywane są zewnętrzne dane. Algorytmy ML potrafią wyciągać wnioski z danych uczących i dokonywać predykcji na nowych danych.
Uczenie Głębokie (DL ang. Deep Learning) - gałąź ML inspirowana biologicznymi uwarunkowaniami ludzkiego mózgu. Algorytmy DL w odróżnieniu od ML potrafią same wybrać odpowiednie cechy z zadanych danych. Wiąże się to z tym, że DL wymaga silniejszych jednostek obliczeniowych (GPU, TPU) oraz znacznie większej ilości danych.
Gdzie wykorzystujemy Machine Learning?¶
Główne zastosowania ML:
Regresja - predykcja wartości na podstawie innych informacji.

Klasyfikacja - predykcja klas na podstawie etykietowanych danych uczących

Klasteryzacja - predykcja klas i dopasowanie ich struktury na podstawie nieetykietowanych danych uczących

W jaki sposób to działa?¶

Wczytanie danych - Boston House Pricing¶
13 predyktorów opisujących domy i ich okolicę, 506 obserwacji (wspóczynnik przestępczości, stosunek liczby uczniów do nauczycieli, liczba pokoi itp.)
import sklearn
from sklearn.datasets import load_boston
import pandas as pd
import numpy as np
np.random.seed(123)
boston_dict = load_boston()
print(boston_dict.keys())
boston=pd.DataFrame(boston_dict.data)
boston.columns=boston_dict.feature_names
print(boston.head())
X = boston
Y = pd.DataFrame(boston_dict.target)
Analiza Danych¶
import seaborn as sns
import matplotlib.pyplot as plt
sns.pairplot(boston.iloc[:,[0,5,10]], size=2)
plt.tight_layout()
#CRIM - współczynnik przestępczości
#RM - liczba pokoi
#PTRATION - stosunek liczby uczniów do liczby nauczycieli
Preprocessing danych
- standaryzacja
- feature selection
Losowy podział na zbiór treningowy i testowy
from sklearn import model_selection
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X, Y, test_size = 0.33, random_state = 5)
print("Rozmiar zbioru treningowego - predyktory:",X_train.shape,"Rozmiar zbioru treningowego - etykiety:", Y_train.shape )
print("Rozmiar zbioru testowego - predyktory:",X_test.shape,"Rozmiar zbioru testowego - etykiety:", Y_test.shape )
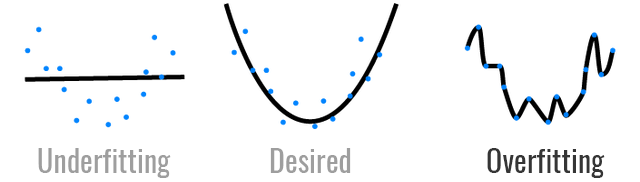
Cel: uniknąć przeuczenia
W przypadku nie wyodrębnienia zbioru testowego trudno rzetelnie ocenić zdolność sieci do predykcji. \
Dodatkowo może wystąpić zjawisko przeuczenia, czyli model idealnie dopasuje się do danych treningowych, natomiast nie będzie miał zdolności do generalizacji.
Regresja Liniowa¶
Zadanie polega na jak najlepszym dopasowaniu prostej do danych, wyrażonej wzorem poniżej ${y_{i}=\beta _{0}1+\beta _{1}x_{i1}+\cdots +\beta _{p}x_{ip}+\varepsilon _{i}=\mathbf {x} _{i}^{\top }{\boldsymbol {\beta }}+\varepsilon _{i},\qquad i=1,\dots ,n}$
Dobór parametrów odbywa się zgodnie z metodą najmniejszych kwadratów.

from sklearn.linear_model import LinearRegression
lm = LinearRegression()
#naucz model na danych treningowych
lm.fit(X_train, Y_train)
print("Współczynniki beta:", lm.coef_)
print(boston_dict.DESCR)
Y_pred_linear = lm.predict(X_test)
def points_plot(Y_test, Y_pred):
fig, ax = plt.subplots(figsize=(7, 5))
ax.scatter(Y_test, Y_pred, label='poprawność modelu')
ax.plot([Y_test.min(), Y_test.max()], [Y_test.min(), Y_test.max()], 'k--', lw=3, label='idealne dopasowanie')
ax.set_xlabel("Ceny rzeczywiste domów [$]")
ax.set_ylabel("Ceny wygenerowane prze model [$]")
ax.set_title("Ceny rzeczywiste vs. wygenerowane")
ax.legend()
plt.show()
points_plot(Y_test, Y_pred_linear)
Metryki:
- pierwiastek z błędu średniokwadratowego
${\operatorname {RMSE} ={\sqrt {\frac {\sum _{i=1}^{n}({\hat {y}}_{i}-y_{i})^{2}}{n}}}}$
im mniejsza wartość, tym lepiej
- współczynnik determinacji [0,1] - określa jak dużo zmienności danych jest uchywycone przez model
${R^{2}={\frac {\sum \limits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}}{\sum \limits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}}$
im wartość bliższa jedności, tym lepiej
import scipy.stats as stats
from sklearn.metrics import r2_score
def metrics (Y_test, Y_pred):
rmse = np.sqrt(sklearn.metrics.mean_squared_error(Y_test, Y_pred))
print("RMSE =",rmse)
r2=r2_score(Y_pred, Y_test)
print("R^2 =",r2)
return rmse,r2
import numpy as np
results=pd.DataFrame() #do agregowania metryk
results['linear']=metrics(Y_test, Y_pred_linear)
error = np.array(Y_pred_linear - Y_test)
plt.hist(error, bins = 20, facecolor='b')
plt.xlabel('wartości błędu [$]')
plt.ylabel('częstość występowania')
plt.figure(figsize=(5,3))
plt.show()
Drzewa regresyjne¶
budowa: korzeń, węzły (m), liście ($m_R$, $m_L$)
wartości w liściach wyliczane są jako średnia z obserwacji
dobór struktury drzewa: szukamy podziału m na $m_L$ i $m_R$, aby SSE($m_L$) + SSE($m_R$) było minimalne
*SSE(.) - suma kwadratów rezyduów, gdy regresja dla (.) estymowana
jest przez średnią próbkową wartości zmiennej objaśnianej dla tego węzła
Strategia wyboru najlepszego drzewa
• utwórz pełne drzewo
• przy różnych parametrach określających koszt złożoności drzew przytnij drzewo
• spośród tak utworzonej skończonej rodziny drzew wybierz drzewo dające najmniejszy błąd w oparciu o kroswalidację
Zaleta:
- interpretowalność
Wada:
- duża wariancja i niestabilność
(małą zmiana w danych może skutkować znaczną zmianą struktury drzewa)
from sklearn import tree
from sklearn.tree import DecisionTreeRegressor
regression_model = DecisionTreeRegressor(criterion="mse", min_samples_leaf=2)
regression_model.fit(X_train,Y_train)
Y_pred_tree = regression_model.predict(X_test)
results['drzewo']=metrics(Y_test, Y_pred_tree)
points_plot(Y_test, Y_pred_tree)
#wizualizacja struktury drzewa
from sklearn.tree import DecisionTreeRegressor, export_graphviz
import graphviz
plt.figure(figsize=(20,20))
splits=tree.plot_tree(regression_model, filled=True)
# #umożliwia dokładną analizę węzłów
# dot_data = tree.export_graphviz(regression_model, out_file=None,
# feature_names=X_train.columns,
# filled=True, rounded=True,
# special_characters=True)
# graph = graphviz.Source(dot_data)
# graph
XGBoost (eXtreme Gradient Boosting)¶
Jest to złożony algorytm, w którym wykorzystano wiele stosowanych wcześniej technik:
- bootstrap - losowanie ze zwracaniem obserwacji z próby
- bagging - stosuje się komitet drzew a następnie wyniki są agregowane (w ten sposób zmniejsza się wariancję modeli)
- boosting - nadawanie obserwacjom bootstrapowym większych wag w trakcie losowania w przypadku gdy jeden z estymator regresji przypisał wartość objaśnianą o dużym błędzie
Minializacja funkcji celu dokonywana jest w oparciu o spadek gradientu.
Zaleta:
- duża skalowalność (używany w CERN)
Wada:
- trudna interpretacja
from xgboost import XGBRegressor, plot_tree
import xgboost as xgb
model = XGBRegressor()
model.fit(X_train, Y_train)
Y_pred_xgb = model.predict(X_test)
points_plot(Y_test, Y_pred_xgb)
results['xgboost']=metrics(Y_test, Y_pred_xgb)
fig, ax = plt.subplots(figsize=(25, 25))
xgb.plot_tree(model, num_trees=4, ax=ax)
plt.show()
# które predyktory są najbardziej informatywne - feature importance
sns.barplot(y=model.feature_importances_, x=boston.columns)
plt.ylabel('Współczynnik informatywności')
plt.xlabel('Predykatory')
plt.xticks(rotation=45)
plt.show()
#LSTAT: procent populacji o niższym statusie społecznym
#RM: liczba pokoi
Wyniki:¶
idx_names = {0:'RMSE', 1:'R^2'}
results1=results.rename(index=idx_names)
results1
PODSUMOWANIE
- Najlepszy okazał się algorytm XGBoost (najmniejsze RMSE i największe R^2)
- Decydując się na ostateczny model warto dobrze przemyśleć wybór metryki
(mogą wskazywać inne modele jako najlepsze/najgorsze) przykład: najgorsze R^2 ma model liniowy podczas gdy największą wartość RMSE daje drzewo
Uwaga: W celu lepszej inwestygacji efektywności modeli wykorzystuje się metodę kroswalidacji
Spostrzeżenie: Niezależnie od zastosowanego algorytmu największe błędy estymacji występują dla najdroższych domów - ok. 50 000$
sns.set()
sns.distplot(Y, bins=22)
plt.show()
#rozkład ma charakter dwumodalny
Zadanie ilustracyjne
- wytrenować model regresji liniowej na całym dostępnym zbiorze: X,Y
(bez podziału na treningowy i testowy)
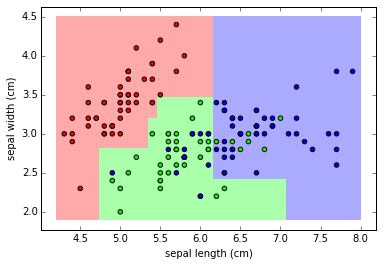
Random Forest Classifier¶
RFC (ang. Random Forest Classifier) Losowy Las Decyzyjny: Zasada działanie RFC polega na tworzeniu komitetu Drzew Decyzjnych i łączy rezultaty ich działania abu uzyskać bardziej precyzyją i stabliną predykcję.

from sklearn import datasets
iris = datasets.load_iris()
print(iris.target_names)
print(iris.feature_names)
from sklearn.model_selection import train_test_split
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=100)
_ = clf.fit(X_train, y_train)
from sklearn.metrics import accuracy_score
print(
f"Accuracy na zbiorze treningowym: {int(100*accuracy_score(y_train, clf.predict(X_train)))}%"
)
print(
f"Accuracy na zbiorze testowym: {int(100*accuracy_score(y_test, clf.predict(X_test)))}%"
)
import pandas as pd
feature_imp = pd.Series(clf.feature_importances_,
index=iris.feature_names).sort_values(ascending=False)
feature_imp
import warnings
warnings.filterwarnings('ignore')
import seaborn as sns
import matplotlib.pyplot as plt # do wizualizacji danych
%matplotlib inline
sns.barplot(y=feature_imp, x=feature_imp.index)
plt.ylabel('Feature Importance Score')
plt.xlabel('Features')
plt.title("Visualizing Important Features")
plt.xticks(rotation=45)
plt.show()
from sklearn.metrics import confusion_matrix
y_pred = clf.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
print(cm)
df_cm = pd.DataFrame(cm, index=iris.target_names, columns=iris.target_names)
sns.set(font_scale=1.4)
grid = sns.heatmap(df_cm,
annot=True,
annot_kws={"size": 16},
fmt='g',
cmap=plt.cm.Blues)
grid.set_title('Confusion matrix')
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.yticks(rotation=0)
grid.xaxis.set_ticks_position('top')
grid.xaxis.set_label_position('top')
plt.show()
X = iris.data[:, 2:
4] #Working with the two first features : sepal length and sepal width
feature_1_name = iris.feature_names[2]
feature_2_name = iris.feature_names[3]
y = iris.target
_ = clf.fit(X, y)
import numpy as np
x_min, x_max = X[:, 0].min() - .1, X[:, 0].max() + .1
y_min, y_max = X[:, 1].min() - .1, X[:, 1].max() + .1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
pred = clf.predict(np.c_[xx.ravel(), yy.ravel()])
pred = pred.reshape(xx.shape)
plt.figure(figsize=(10, 6))
plt.pcolormesh(xx, yy, pred, cmap=plt.get_cmap("Pastel1"))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.get_cmap("Set1"))
plt.xlabel(feature_1_name)
plt.ylabel(feature_2_name)
plt.axis('tight')
plt.show()
Support Vector Machine¶
SVM (ang. Support Vector Machine) - Maszyna wektorów nośnych.
Zasada działania tego algorytmu polega na znalezieniu hiper-płaszczyzny w N-wymiarowej przestrzeni (N to liczba cech, kolumn w naszych danych) która oddzieli i sklasyfikuje punkty ze zbioru dnaych.

Załadujmy dane:
from sklearn.datasets import load_digits
digits = load_digits()
X_train, X_test, y_train, y_test = train_test_split(digits.data,
digits.target,
random_state=0)
Przykałdowy obrazek:
from random import randint
rand = randint(0, digits.target.shape[0])
label = digits.target[rand]
pixels = digits.images[rand]
plt.title(f'Label is {label}')
g = sns.heatmap(pixels, linewidth=0, xticklabels=False, yticklabels=False, cmap='gray', cbar=False, square =True)
plt.show()
print(f"Liczba obrazków: {digits.images.shape[0]}, rozmiar obrazka: {digits.images.shape[1:3]}")
plt.figure(figsize=(10,6))
plt.bar(range(10), np.bincount(y_train))
plt.title("Rozkład przykładów pośród klas")
plt.show()
Nauczmy nasz liniowy model:
from sklearn.svm import LinearSVC
svm = LinearSVC()
_ = svm.fit(X_train, y_train)
print(f"Accuracy na zbiorze traningowym: {int(100*accuracy_score(y_train, svm.predict(X_train)))}%")
print(f"Accuracy na zbiorze testowym: {int(100*accuracy_score(y_test, svm.predict(X_test)))}%")
from sklearn.metrics import confusion_matrix
y_pred = svm.predict(X_test)
cm = confusion_matrix(y_test, y_pred)
df_cm = pd.DataFrame(cm, index = range(10), columns = range(10))
sns.set(font_scale=1.4)
grid = sns.heatmap(df_cm, annot=True,annot_kws={"size": 16}, fmt='g', cmap=plt.cm.Blues)
grid.set_title('Confusion matrix')
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.yticks( rotation=0)
grid.xaxis.set_ticks_position('top')
grid.xaxis.set_label_position('top')
plt.show()
Klasyfikacja z użyciem perceptronu¶
Współczesne osiągnięcia sztucznej inteligencji to w dużej mierze załuga uczenia głębokiego (ang. deep learning) a w szczególności sieci neuronowych. Najbardziej podstawową architekturą sieci neuronowej jest Perceptron Wielowarstwowy. Standardowe sieci używane w biznesie lub nauce składją się z dziesiętek lub setek tysięcy neuronów. Poniżej przedstawię zasadę działania pojedynczego neuronu.
Budowa neuronu:

Feedforward - algorytm propagacji w przód:
$z=w_1x_1+w_2x_2+b$
$p=sigmoid(z)$
$c=(p-y)^2$
Backpropagation - algorytm propagacji błędu wstecz:
Algorytm propagacji wstecznej polega na propagacji błędu jakim obarczona została predykcja wstecz względem kierunku propagacji feedforward
$w_1 = w_1 - learning\_rate \cdot \frac{\partial c}{\partial w_1}$
$w_2 = w_2 - learning\_rate \cdot \frac{\partial c}{\partial w_2}$
$b = b - learning\_rate \cdot \frac{\partial c}{\partial b}$
Z reguły łańcuchowej:
$\frac{\partial c}{\partial w_1} = \frac{\partial c}{\partial p} \cdot \frac{\partial p}{\partial z} \cdot \frac{\partial z}{\partial w_1}$
$\frac{\partial c}{\partial w_2} = \frac{\partial c}{\partial p} \cdot \frac{\partial p}{\partial z} \cdot \frac{\partial z}{\partial w_2}$
$\frac{\partial c}{\partial b} = \frac{\partial c}{\partial p} \cdot \frac{\partial p}{\partial z} \cdot \frac{\partial z}{\partial b}$
Liczymy różniczki:
$\frac{\partial c}{\partial p} = 2(p-y)$
$\frac{\partial p}{\partial z} = sigmoid'(z)$
$\frac{\partial z}{\partial w_1} = x_1$
$\frac{\partial z}{\partial w_2} = x_2$
$\frac{\partial z}{\partial b} = 1$
Funkcja Aktywacji:
$sigmoid(z) = \frac{1}{1+e^{-z}}$
$sigmoid'(z) = sigmoid(z) \cdot (1- sigmoid(z))$
def load_data(f1,f2):
iris = datasets.load_iris()
X = iris.data[:, (f1,f2)]
y = iris.target
X = X[y != 2]
y = y[y != 2]
feature_1_name = iris.feature_names[f1]
feature_2_name = iris.feature_names[f2]
return X,y, feature_1_name, feature_2_name
f1,f2 = 0,1
X, y, feature_1_name, feature_2_name = load_data(f1,f2)
print("Selected features: ", feature_1_name, feature_2_name)
my_flower = np.asarray([[6.5, 3.5]])
plt.figure(figsize=(8, 8))
plt.scatter(X[:, 0], X[:, 1], c=y, s=100, edgecolor='k', cmap=plt.cm.Set1)
plt.scatter([my_flower[0][0]], [my_flower[0][1]],
c='g',
edgecolor='k',
marker='d',
s=200)
plt.xlabel(feature_1_name)
plt.ylabel(feature_2_name)
plt.show()
Funkcja aktywacji
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def d_sigmoid(x):
return sigmoid(x) * (1 - sigmoid(x))
ls = np.linspace(-5, 5, 100)
plt.plot(ls, sigmoid(ls), "red") # sigmoid in blue
plt.plot(ls, d_sigmoid(ls), "gray") # d_sigmoid in red
plt.show()
Implementacja Sieci Neuronowej
class NNClassifier:
def cost(self):
c = 0
for j in range(len(self.X)):
pred = self.predict(X[j])
c += np.square(pred - self.y[j])
return c
def random_example(self):
ri = np.random.randint(len(self.X))
return self.X[ri], self.y[ri]
def fit(self, X, y, plot=False, iterations=10_000, learning_rate=0.1):
#Losowa inicjalizacja zmiennych
self.w1 = np.random.randn()
self.w2 = np.random.randn()
self.b = np.random.randn()
self.X = X
self.y = y
costs = [] # Lista przechowywująca wartości funkcji kosztu
for i in range(iterations):
point, target = self.random_example()
# Co każde 100 iteracji badaj funkcję kosztu
if i % 100 == 0:
costs.append(self.cost())
z = point[0] * self.w1 + point[1] * self.w2 + self.b
pred = sigmoid(z)
dcost_dpred = 2 * (pred - target)
dpred_dz = d_sigmoid(z)
dz_dw1 = point[0]
dz_dw2 = point[1]
dz_db = 1
dcost_dz = dcost_dpred * dpred_dz
dcost_dw1 = dcost_dz * dz_dw1
dcost_dw2 = dcost_dz * dz_dw2
dcost_db = dcost_dz * dz_db
self.w1 = self.w1 - learning_rate * dcost_dw1
self.w2 = self.w2 - learning_rate * dcost_dw2
self.b = self.b - learning_rate * dcost_db
if plot:
plt.figure(figsize=(8, 5))
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.plot(costs)
plt.show()
def predict(self, x):
if isinstance(x,tuple):
x = np.asarray(x)
if len(x.shape) == 1:
x = np.asarray([x])
z = self.w1 * x[:,0] + self.w2 * x[:,1] + self.b
pred = sigmoid(z)
pred = np.where(pred >= 0.5, 1, 0)
return pred
nnc = NNClassifier()
nnc.fit(X, y, plot=True)
Predykcja dla nowego przypadku
my_flower = (6.5, 3.5)
pred = nnc.predict(my_flower)
print("0 - red, 1 -> gray")
pred_col = 'gray' if pred.item() > 0.5 else 'red'
print(f"{pred.item()} -> {pred_col}")
Wizualizacja predykcji sieci neuronowej
f1,f2 = 2,3
X, y, feature_1_name, feature_2_name = load_data(f1,f2)
nnc.fit(X, y)
x_min, x_max = X[:, 0].min() - .1, X[:, 0].max() + .1
y_min, y_max = X[:, 1].min() - .1, X[:, 1].max() + .1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100),
np.linspace(y_min, y_max, 100))
plt.figure(figsize=(10,6))
pred = nnc.predict(np.c_[xx.ravel(), yy.ravel()])
pred = pred.reshape(xx.shape)
plt.pcolormesh(xx, yy, pred, cmap=plt.get_cmap("Pastel1"))
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.get_cmap("Set1"))
plt.xlabel(feature_1_name)
plt.ylabel(feature_2_name)
idx = np.random.randint(np.c_[xx.ravel(), yy.ravel()].shape[0], size=1)
my_flower = np.c_[xx.ravel(), yy.ravel()][idx,:]
pred_flower = nnc.predict(my_flower)
pred_col = 'gray' if pred_flower.item() > 0.5 else 'red'
plt.scatter([my_flower[0][0]], [my_flower[0][1]],
c=pred_col,
edgecolor='k',
marker='d',
s=200)
plt.show()
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets, cluster, metrics
from sklearn.preprocessing import StandardScaler
from itertools import islice, cycle
import warnings
Generowanie danych
n_samples = 2000
warnings.filterwarnings("ignore", message="Graph is not fully connected, spectral embedding" +
" may not work as expected.", category=UserWarning)
noisy_circles = datasets.make_circles(n_samples=n_samples, factor=.5, noise=.05)
noisy_moons = datasets.make_moons(n_samples=n_samples, noise=.05)
varied = datasets.make_blobs(n_samples=n_samples, cluster_std=[1.0, 2.5, 0.5], random_state=170)
blobs = datasets.make_blobs(n_samples=n_samples, random_state=8)
no_structure = np.random.rand(n_samples, 2), None
datasets = [
(noisy_circles, {'n_clusters': 2, 'eps': .3}),
(noisy_moons, {'n_clusters': 2, 'eps': .3}),
(varied, {'n_clusters': 3, 'eps': .18}),
(blobs, {'n_clusters': 3, 'eps': .3}),
(no_structure, {'n_clusters': 3, 'eps': .3})]
Wizualizacja wygenerowanych danych
plt.rcParams["figure.figsize"] = (15, 15)
for id_dataset, dataset in enumerate(datasets):
plt.subplot(3, 3, id_dataset+1)
plt.scatter(dataset[0][0][:, 0], dataset[0][0][:, 1], s=10)
plt.show()
Interfejs
results = {}
def clustering(algorithm, dataset, id_data):
X, Y = dataset
X = StandardScaler().fit_transform(X)
algorithm.fit(X)
y_pred = algorithm.labels_.astype(np.int)
colors = np.array(list(islice(cycle(['#377eb8', '#ff7f00', '#4daf4a']), int(max(y_pred) + 1))))
colors = np.append(colors, ["#000000"])
plt.subplot(3, 3, id_data+1)
plt.scatter(X[:, 0], X[:, 1], s=10, color=colors[y_pred])
return {'input': X, 'labels': Y, 'predictions': y_pred}
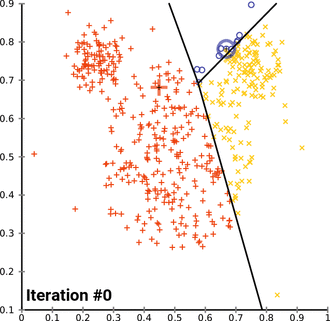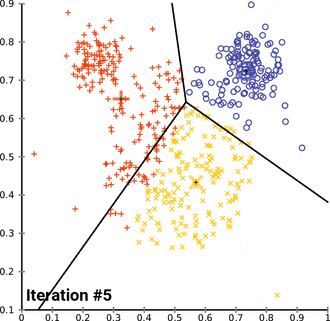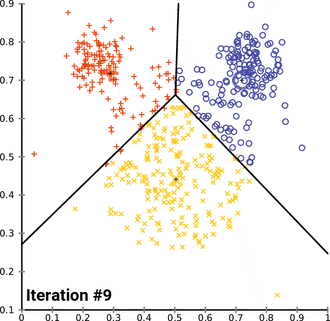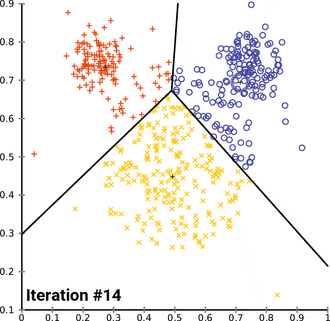
KMeans¶
KMeans - algorytm uczenia nienadzorowanego (nieetykietowane dane). Algorytm ustawia losowo wygenerowane centroidy (centra poszukiwanych klastrów), następnie powtarza dwa poniższe kroki:
1. Przypisanie danych do klastrów:
Każdy centroid odpowiada dokładnie jednemu klastrowi. Każdemu z punktów w przestrzeni danych przypisywany jest jeden- najbliższy centroid. Następnie obliczany jest koszt tego przypisania na podstawie odległości euklidesowej.
2. Uaktualnienie położenia centroidów
W tym kroku obliczana jest nowa pozycja centroidu na podstawie środka masy przypisanych mu punktów.
results['KMeans'] = []
for id_data, (dataset, params) in enumerate(datasets):
kmeans = cluster.KMeans(n_clusters=params['n_clusters'])
results['KMeans'].append(clustering(kmeans, dataset, id_data))
plt.show()
DBScan¶
Algorytm DBScan działa nieco inaczej, ponieważ zamiast szukać centrów ośrodków o maksymalnym zagęszczeniu, łączy punkty które mogę stworzyć taki ośrodek.
Potrzebne mu są do tego dwa parametry:
- eps: minimalna odległość między dwoma punktami - jeżeli dwa punkty są odległe o mniej niż eps to są uznawane za sąsiadów.
- minPoints: minimalna ilość punktów która może stworzyć nnowy gęsty region.

results['DBSCAN'] = []
for id_data, (dataset, params) in enumerate(datasets):
dbscan = cluster.DBSCAN(eps=params['eps'])
results['DBSCAN'].append(clustering(dbscan, dataset, id_data))
plt.show()
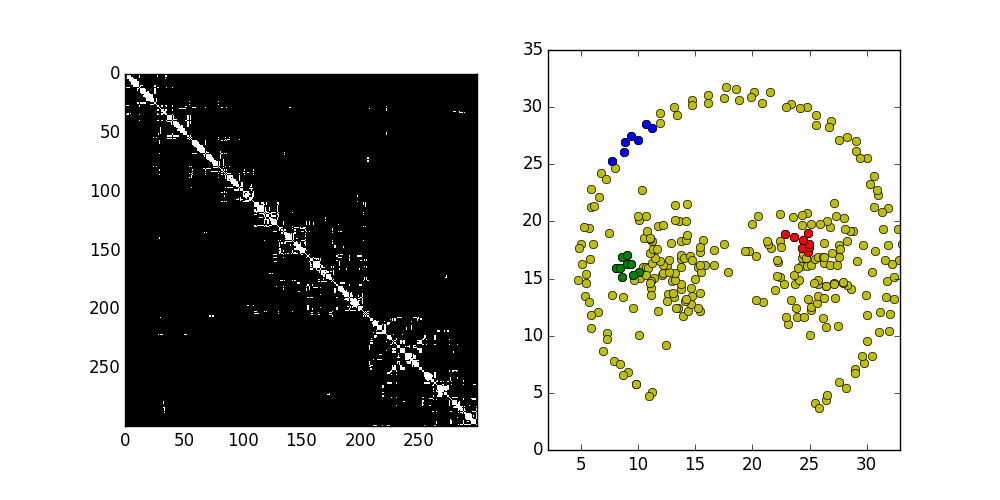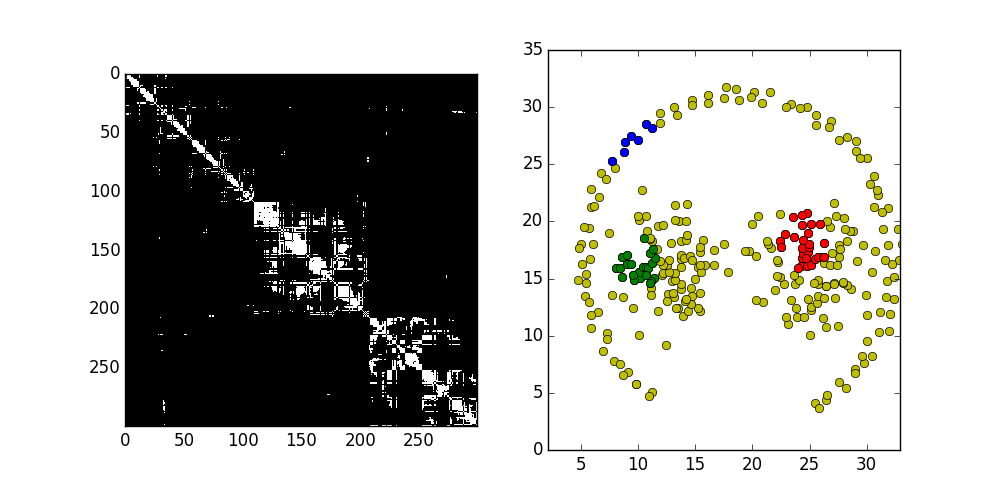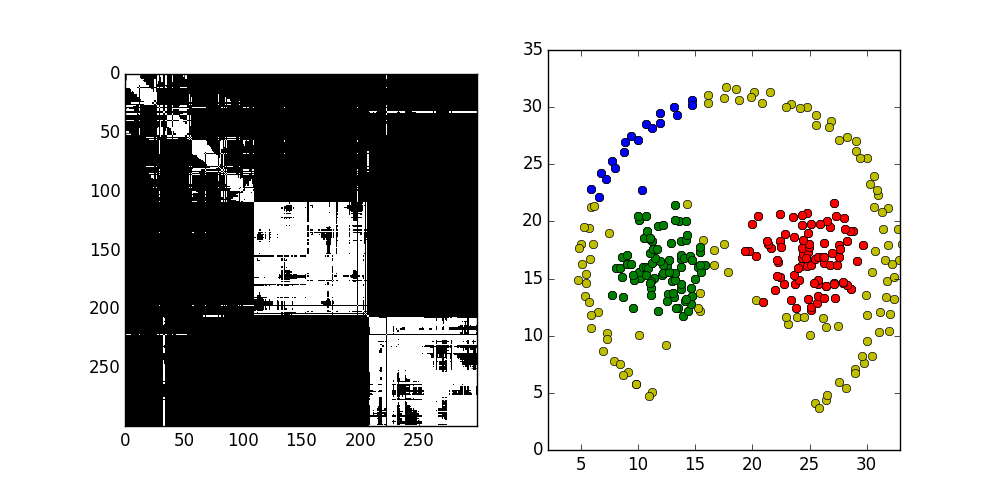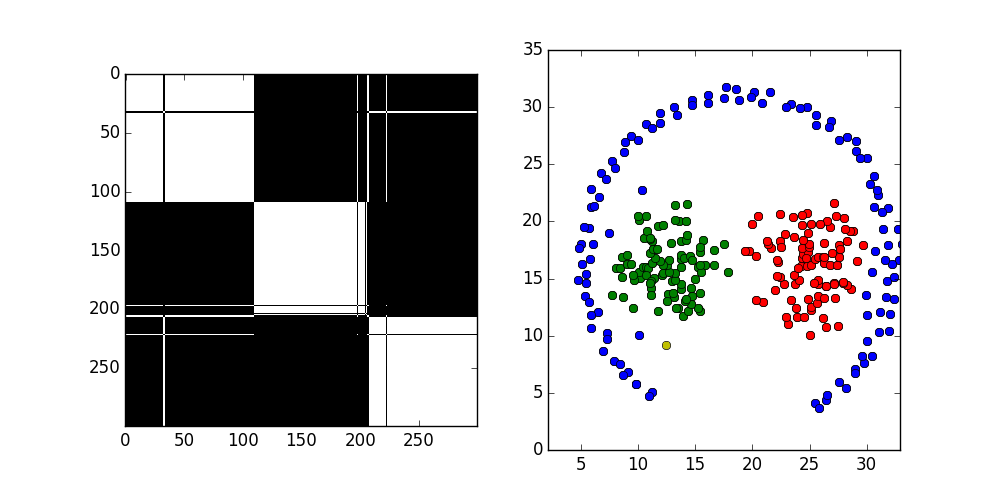
Spectral Clustering¶
Spectral Clustering podobine jak DBScan polega na wyszukiwaniu połączeń między danymi i grupowaniu ich na podstawie ich ilości w grupie. Zasada działania jest jednak nieco inna. Zaczynamy od wyznaczenia grafu połączeń, gdzie wagi na krawędziach są proporcjonalne do odległości między punktami.

Słabe połączenia zostaną w przyszłości odcięte dzięki czemu utworzą się podgrafy tworzący poszukiwane klastry.

Odpowiednie przekształcenie macierzy połączeń pozwala uzyskać oczekiwaną liczbę klastrów.

results['Spectral'] = []
for id_data, (dataset, params) in enumerate(datasets):
spectral = cluster.SpectralClustering(n_clusters=params['n_clusters'], eigen_solver='arpack', affinity="nearest_neighbors")
results['Spectral'].append(clustering(spectral, dataset, id_data))
plt.show()
Metody oceny klasteryzacji
Normalized mutual info score - to znormalizowana Mutual Information (MI) o zakresie od 0 (brak wzajemnej informacji - z punktu widzenia teorii informacji) do 1 (idealna korelacja).
def nmi_score(labels, predictions):
if not (labels is None):
return metrics.normalized_mutual_info_score(labels, predictions,
average_method='arithmetic')
else:
return 'nan'
Fowlkes-Mallows score - miara podobieństwa dwóch klastrów
def fm_score(labels, predictions):
if not (labels is None):
return metrics.fowlkes_mallows_score(labels, predictions)
else:
return 'nan'
Silhouette score - Wskaźnik Silhouette może być używany do określenia dystansu dzielącego uzyskane klastry. Wynik bliski 1 oznacza dużą odległość danego punktu od klastra sąsiedniego. Wynik bliski -1 oznacza przypisanie do złego klastra.
def silhouette_score(inputs, predictions):
if len(set(predictions)) > 1:
return metrics.silhouette_score(inputs, predictions,
metric='euclidean')
else:
return 'nan'
scores = {}
for key, value in results.items():
scores[key] = {}
scores[key]['nmi'] = []
scores[key]['fm'] = []
scores[key]['silhouette'] = []
for algorithm_results in value:
inputs, labels, predictions = \
algorithm_results['input'], algorithm_results['labels'], algorithm_results['predictions']
scores[key]['nmi'].append(nmi_score(labels, predictions))
scores[key]['fm'].append(fm_score(labels, predictions))
scores[key]['silhouette'].append(silhouette_score(inputs, predictions))
kmeans_metrics = pd.DataFrame(data=scores['KMeans'])
print(kmeans_metrics)
for id_data, (dataset, params) in enumerate(datasets):
clustering(kmeans, dataset, id_data)
dbscan_metrics = pd.DataFrame(data=scores['DBSCAN'])
print(dbscan_metrics)
for id_data, (dataset, params) in enumerate(datasets):
clustering(dbscan, dataset, id_data)
spectral_metrics = pd.DataFrame(data=scores['Spectral'])
print(spectral_metrics)
for id_data, (dataset, params) in enumerate(datasets):
clustering(spectral, dataset, id_data)